当前位置： 首页 > news >正文

机器学习 day30（正则化参数λ对模型的影响）

news 2026/2/8 15:20:52
  1. λ对Jcv和Jtrain的影响
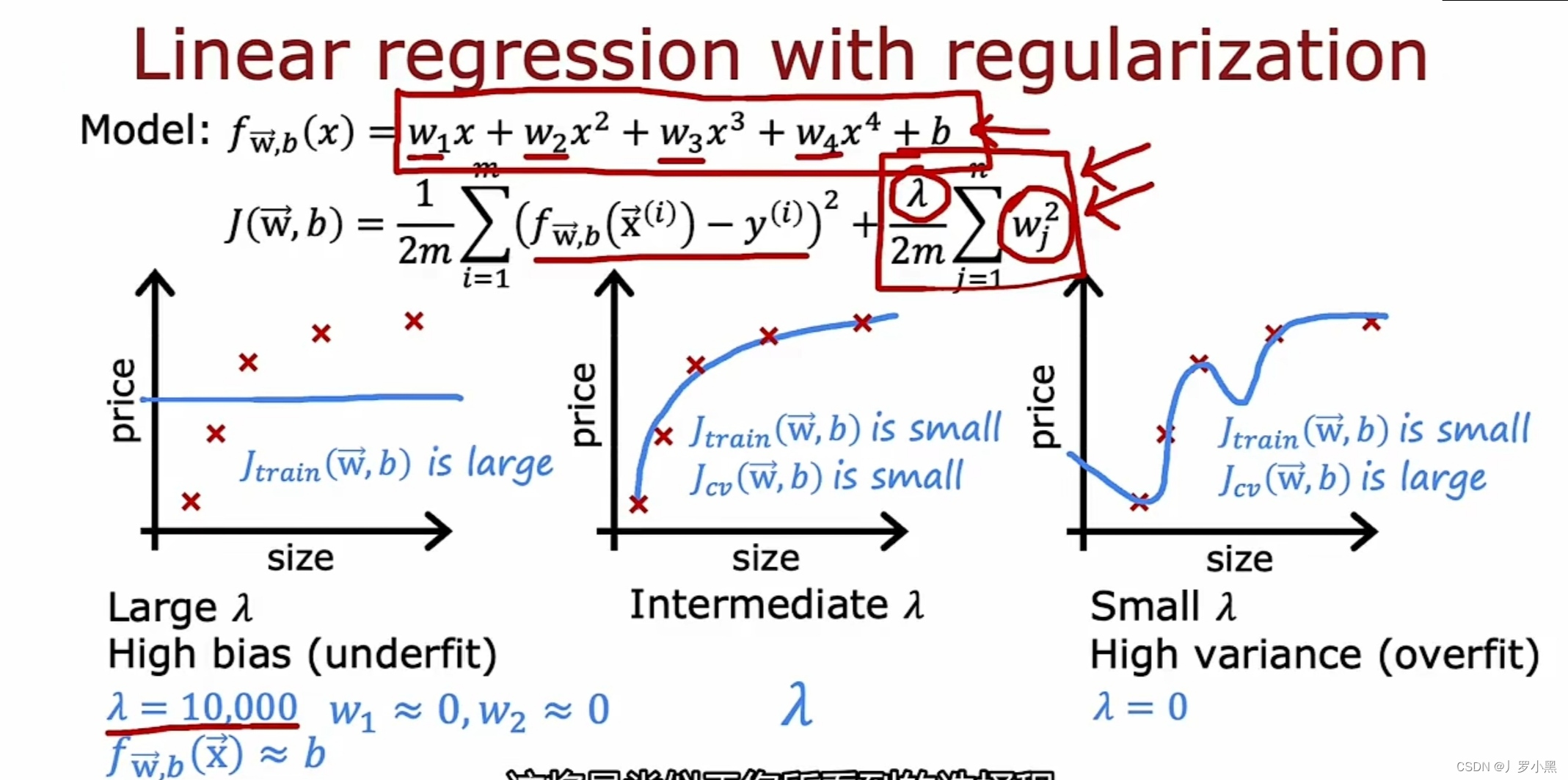
    在这里插入图片描述
  • 假设该模型为四阶多项式
  • 当λ很大时，在最小化J的过程中，w会很小且接近0，此时模型f(x)近似于一个常数，所以此时模型欠拟合，Jtrain和Jcv都很大
  • 当λ很小时，表示模型几乎没有正则化，而四阶多项式的模型十分弯曲，所以此时模型过拟合，Jtrain很小，Jcv远大于Jtrain
  • 当λ取中间值，模型刚好拟合良好、泛化良好，此时Jtrain很小、Jcv也很小
  1. 如何选择一个合适的λ
    在这里插入图片描述
  • 第一次，假设λ为0，最小化成本函数J后得到一组w、b，之后计算这组参数对应的Jcv
  • 第二次，假设λ为0.01，最小化成本函数J后得到一组w、b，之后计算这组参数对应的Jcv
  • …以此类推，例如：第十二次，假设λ为10…
  • 通过这些不同λ对应的Jcv的值，来选择一个最小的Jcv对应的λ值，此时的λ为正则化参数的最佳值
  • 此例中，如果第5次的Jcv最小，则我们选择第5次的λ、w、b，最后可以选择输出第5次的模型所对应的Jtest值，即该模型的test泛化能力
  1. λ如何影响Jtrain和Jcv
    在这里插入图片描述
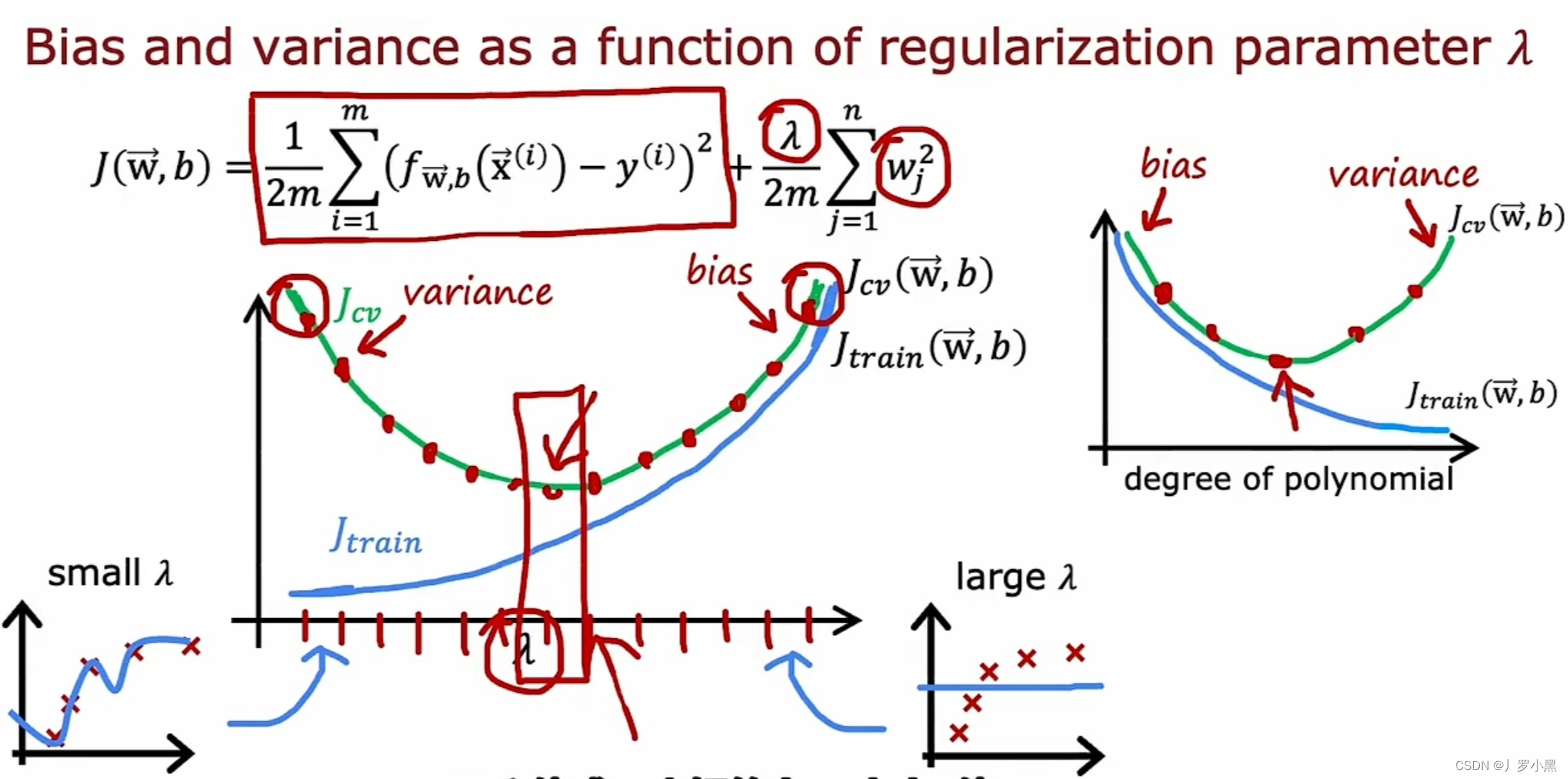
  • λ对Jtrain和Jcv的影响如上图所示，此图近似看作d对Jtrain和Jcv的影响图的镜像，
  • 通过最小Jcv，可以帮助选择一个合适的λ、d，从而帮助选择合适的模型（泛化良好、拟合良好）

相关文章：

机器学习 day30（正则化参数λ对模型的影响）

λ对Jcv和Jtrain的影响 假设该模型为四阶多项式当λ很大时，在最小化J的过程中，w会很小且接近0，此时模型f(x)近似于一个常数，所以此时模型欠拟合，Jtrain和Jcv都很大当λ很小时，表示模型几乎没有正则化&…...

编程日记 2023/7/28 5:39:14

图文教程：如何在 3DS Max 中创建3D迷你卡通房屋

推荐： NSDT场景编辑器助你快速搭建可二次开发的3D应用场景 在本教程中，我们将学习如何创建一个有趣的、低多边形的迷你动画房子，你可以在自己的插图或视频游戏项目中使用它。您将学习的一些技能将包括创建基本的3D形状和基本的建模技术。让我…...

编程日记 2023/7/28 5:38:13

根据UIL下载图片/视频、根据URL自动下载图片/视频、GUI自动下载想要的图片

目录 1，根据UIL下载图片/视频 2，根据URL自动下载图片/视频 3、GUI自动下载想要的图片 ①点击下载按钮，进行挨个下载 ②右击保存进行下载图片 4、图片或视频URL批量放入浏览器页面上 1，根据UIL下载图片/视频 def downForInter…...

编程日记 2023/7/28 5:37:12

HTML ＜picture＞ 标签

实例 如何使用 <picture> 标签： <picture><source media="(min-width:650px)" srcset="/i/photo/flower-4.jpg"><source media="(min-width:465px)" srcset="/i/photo/tulip.jpg"><img src="/i/ph…...

编程日记 2023/7/28 5:36:11

力扣天天练--week3-LeetCode75

topic75-9-t443:压缩字符串 题目描述&#xff1a; 给你一个字符数组 chars &#xff0c;请使用下述算法压缩&#xff1a; 从一个空字符串 s 开始。对于 chars 中的每组 连续重复字符 &#xff1a; 如果这一组长度为 1 &#xff0c;则将字符追加到 s 中。 否则&#xff0c;需…...

编程日记 2023/7/28 5:35:10

5.2 方法的定义和调用

5.2 方法的定义和调用 Java的方法类似于其他语言的函数&#xff0c;是一段用来完成特定功能的代码片段&#xff0c;一般情况下&#xff0c;定义一个方法包含以下语法&#xff1a; 一、方法的定义 方法包含一个方法头和一个方法体 修饰符 返回值类型 方法名 &#xff08;参数类…...

编程日记 2023/7/28 5:34:07

Linux基础以及常用命令

目录 1 Linux简介1.1 不同应用领域的主流操作系统1.2 Linux系统版本1.3 Linux安装1.3.1 安装VMWare1.3.2 安装CentOS镜像1.3.3 网卡设置1.3.4 安装SSH连接工具1.3.5 Linux和Windows目录结构对比 2 Linux常用命令2.0 常用命令&#xff08;ls&#xff0c;pwd&#xff0c;cd&#…...

编程日记 2023/7/28 5:33:06

echarts 折线图上只显示某一个点值

<template> <div> <!-- 数据来源 --> <div class"echarts" ref"echartsRef"></div> </div> </template> <script setup langts name"reconciled"> import { ref } from "vue"; im…...

编程日记 2023/7/28 5:32:05

1、传统锁回顾（Jvm本地锁，MySQL悲观锁、乐观锁）

目录 1.1 从减库存聊起1.2 环境准备1.3 简单实现减库存1.4 演示超卖现象1.5 jvm锁1.6 三种情况导致Jvm本地锁失效1、多例模式下&#xff0c;Jvm本地锁失效2、Spring的事务导致Jvm本地锁失效3、集群部署导致Jvm本地锁失效 1.7 mysql锁演示1.7.1、一个sql1.7.2、悲观锁1.7.3、乐观…...

编程日记 2023/7/28 5:31:03

【Java||牛客】DFS应用迷宫问题

step by step. 题目&#xff1a; 描述 定义一个二维数组 N*M &#xff0c;如 5 5 数组下所示&#xff1a; int maze[5][5] { 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, }; 它表示一个迷宫&#xff0c;其中的1表示墙壁&#xff0c;0表示可…...

编程日记 2023/7/28 5:30:01

【vue】Vue中class样式的动态绑定

简介&#xff1a;Vue中class样式的绑定 1、字符串写法 使用场景&#xff1a;样式的类型不确定 写法&#xff1a; <div :class"xd_bg">测试账号</div> 手动触发样式改变 注意&#xff1a;字符串使用的是vue实例data中已有的属性 2、对象写法 使…...

编程日记 2023/7/28 5:28:59

机器学习深度学习——随机梯度下降算法（及其优化）

在我们没有办法得到解析解的时候&#xff0c;我们可以用过梯度下降来进行优化&#xff0c;这种方法几乎可以所有深度学习模型。 关于优化的东西&#xff0c;我自己曾经研究过智能排班算法和优化&#xff0c;所以关于如何找局部最小值&#xff0c;以及如何跳出局部最小值的一些基…...

编程日记 2023/7/28 5:27:58

【MTK平台】【wpa_supplicant】关于wpa_supplicant_8/src/p2p/p2p.c文件的介绍

本文主要介绍external/wpa_supplicant_8/src/p2p/p2p.c文件 先看下p2p_find 这个方法 P2P_find 主要用于 P2P&#xff08;点对点&#xff09;网络中查找其他对等方的功能。另外可以看到设置P2P模块的状态为 P2P_SEARCH int p2p_find(struct p2p_data *p2p, unsigned int tim…...

编程日记 2023/7/28 5:26:57

华为数通HCIP-流量过滤与转发路径控制

流量控制 分类&#xff1a;流量过滤、流量转发路径控制&#xff1b; 特点&#xff1a;1、作用于数据层面/转发层面&#xff1b; 2、不会影响路由表&#xff0c;针对转发流量生效&#xff1b; 实现步骤&#xff1a; 1、通过流量匹配工具匹配流量&#xff08;ACL…...

编程日记 2023/7/28 5:25:55

SpringBoot中定时任务开启多线程避免多任务堵塞

场景 SpringBoot中定时任务与异步定时任务的实现&#xff1a; SpringBoot中定时任务与异步定时任务的实现_霸道流氓气质的博客-CSDN博客 使用SpringBoot原生方式实现定时任务&#xff0c;已经开启多线程支持&#xff0c;以上是方式之一。 除此之外还可通过如下方式。 为什…...

编程日记 2023/7/28 5:24:54

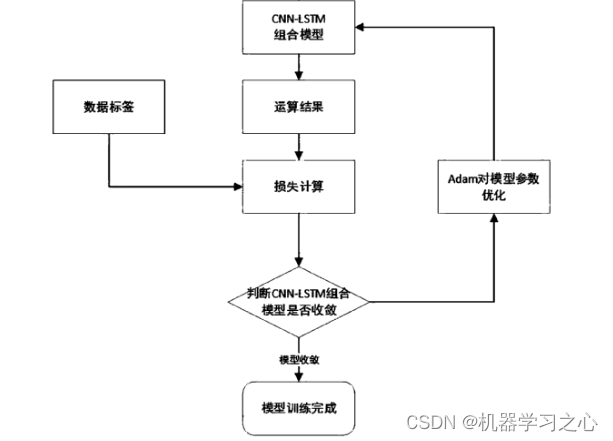
回归预测 | MATLAB实现SO-CNN-BiLSTM蛇群算法优化卷积双向长短期记忆神经网络多输入单输出回归预测

回归预测 | MATLAB实现SO-CNN-BiLSTM蛇群算法优化卷积双向长短期记忆神经网络多输入单输出回归预测 目录 回归预测 | MATLAB实现SO-CNN-BiLSTM蛇群算法优化卷积双向长短期记忆神经网络多输入单输出回归预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 Matlab实…...

编程日记 2023/7/28 5:23:53

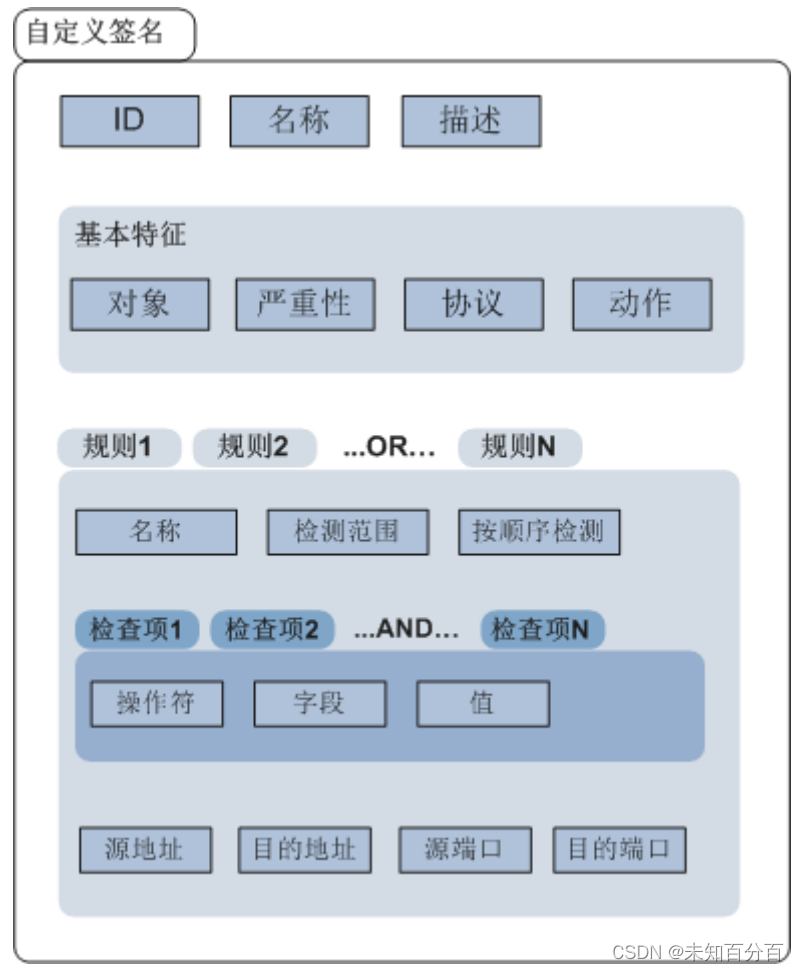
入侵检测——IDS概述、签名技术

1. 什么是IDS&#xff1f; IDS&#xff08;intrusion detection system&#xff09;入侵检测系统&#xff0c;是一种对网络传输进行即时监视&#xff0c;在发现可疑传输时发出警报或者采取主动反应措施的网络安全设备。它会对系统的运行状态进行监视&#xff0c;发现各种攻击企…...

编程日记 2023/7/28 5:22:51

golang 标准库json Marshal 序列化与反序列化

标准库代码 func Marshal(v any) ([]byte, error) {e : newEncodeState()defer encodeStatePool.Put(e)err : e.marshal(v, encOpts{escapeHTML: true})if err ! nil {return nil, err}buf : append([]byte(nil), e.Bytes()...)return buf, nil }func Unmarshal(data []byte, …...

编程日记 2023/7/28 5:21:49

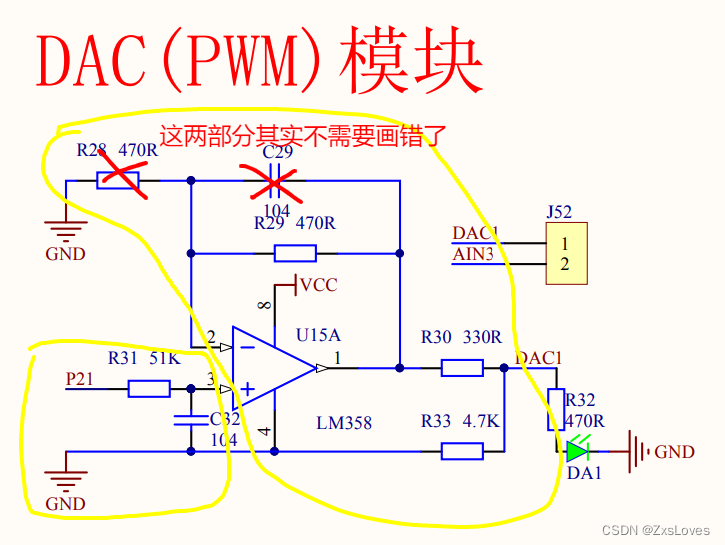
【【51单片机AD/DA的分析】】

51单片机AD/DA的分析 看似单片机实验&#xff0c;其实是要学好数电 模数转换 与 数模转换 运算放大器 DA的转换就是利用运算放大器实现的 输出电压v0-(D7~D0)/256 x (VrefxRfb)/R D7~D0 就是我们控制的按键看输入多少 然后再划分256份 Vref是我们设置的一个基准电压 PWM 这种…...

编程日记 2023/7/28 5:20:48

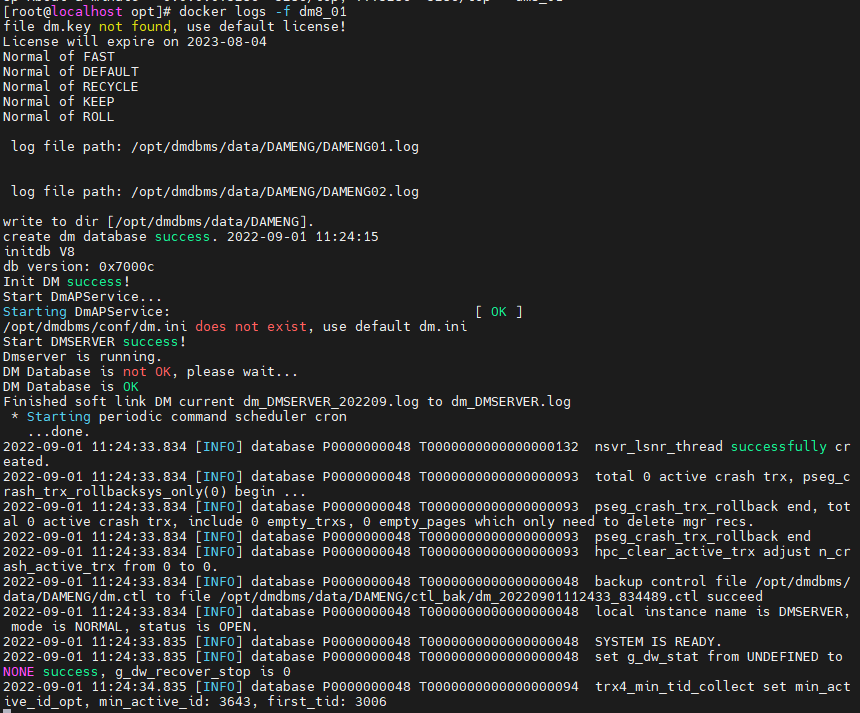
在docker中安装使用达梦数据库

关于在docker中安装达梦数据库&#xff0c;达梦官方网站其实是有提供安装使用方法的&#xff0c;但可能还是有朋友不会&#xff0c;这里将在原文基础上简单扩充下。 注意&#xff1a;docker容器中&#xff0c;数据库安装后没有创建服务的脚本&#xff0c;只有bin、bin2、conf、…...

编程日记 2023/7/28 5:19:47

后进先出（LIFO）详解

LIFO 是 Last In, First Out 的缩写&#xff0c;中文译为后进先出。这是一种数据结构的工作原则&#xff0c;类似于一摞盘子或一叠书本&#xff1a; 最后放进去的元素最先出来 -想象往筒状容器里放盘子&#xff1a; &#xff08;1&#xff09;你放进的最后一个盘子&#xff08…...

编程新知 2026/2/8 1:22:58

网络六边形受到攻击

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 抽象 现代智能交通系统 &#xff08;ITS&#xff09; 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 &#xff08;…...

编程新知 2026/2/8 5:22:04

Swift 协议扩展精进之路：解决 CoreData 托管实体子类的类型不匹配问题（下）

概述 在 Swift 开发语言中&#xff0c;各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过&#xff0c;在涉及到多个子类派生于基类进行多态模拟的场景下&#xff0c;…...

编程新知 2026/1/23 4:56:05

【机器视觉】单目测距——运动结构恢复

ps&#xff1a;图是随便找的&#xff0c;为了凑个封面 前言 在前面对光流法进行进一步改进&#xff0c;希望将2D光流推广至3D场景流时&#xff0c;发现2D转3D过程中存在尺度歧义问题&#xff0c;需要补全摄像头拍摄图像中缺失的深度信息&#xff0c;否则解空间不收敛&#xf…...

编程新知 2026/2/8 3:03:01

在Ubuntu中设置开机自动运行（sudo）指令的指南

在Ubuntu系统中&#xff0c;有时需要在系统启动时自动执行某些命令&#xff0c;特别是需要 sudo权限的指令。为了实现这一功能&#xff0c;可以使用多种方法&#xff0c;包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法&#xff0c;并提供…...

编程新知 2025/12/23 11:20:24

Java面试专项一-准备篇

一、企业简历筛选规则 一般企业的简历筛选流程&#xff1a;首先由HR先筛选一部分简历后&#xff0c;在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如&#xff1a;Boss直聘&#xff08;招聘方平台&#xff09; 直接按照条件进行筛选 例如&#xff1a…...

编程新知 2026/1/26 19:10:48

图表类系列各种样式PPT模版分享

图标图表系列PPT模版&#xff0c;柱状图PPT模版&#xff0c;线状图PPT模版&#xff0c;折线图PPT模版&#xff0c;饼状图PPT模版&#xff0c;雷达图PPT模版&#xff0c;树状图PPT模版 图表类系列各种样式PPT模版分享&#xff1a;图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

编程新知 2026/2/4 18:07:02

AspectJ 在 Android 中的完整使用指南

一、环境配置&#xff08;Gradle 7.0 适配&#xff09; 1. 项目级 build.gradle // 注意&#xff1a;沪江插件已停更&#xff0c;推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

编程新知 2025/7/7 22:33:57

回溯算法学习

一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

编程新知 2026/1/24 12:01:38

【Go语言基础【13】】函数、闭包、方法

文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数&#xff08;函数作为参数、返回值&#xff09; 三、匿名函数与闭包1. 匿名函数&#xff08;Lambda函…...

编程新知 2025/12/8 19:02:25