梯度下降法和牛顿法
梯度下降法和牛顿法都是优化方法。
梯度下降法
梯度下降法和相关知识可以参考导数、偏导数、梯度、方向导数、梯度下降、二阶导数、二阶方向导数一文。梯度下降法是一种迭代地每次沿着与梯度相反方向前进的不断降低损失函数的优化方法。梯度下降只用到一阶导数的信息,没有参考二阶导数的信息。
当自变量有多维时,如果某点二阶导数矩阵的最大特征值和最小特征值差别较大(二阶导数的信息),也就是说在一个自变量维度上一阶导数下降的很快,另一个自变量维度上一阶导数下降的很慢,慢的那个维度会拖累快的维度,导致整体迭代速度较慢。并且此时学习率设置的较小才会避免迭代过程中在二阶导大的方向不经过最低点而跳到对向这样来回跳动,但是此时学习率较小同时会导致在二阶导小的方向迭代较慢。在这种情况下,选择一个好的学习率是一件比较困难的事情。
如下图所示,(1,1)方向是二阶导最大的方向(最陡),(1,-1)方向是二阶导最小的方向(最缓),红色的线是梯度下降的路线,可以看到路线在(1,1)方向反复来回跳动(不断跳到对向)。梯度下降在这种情况下的表现有瑕疵。

牛顿法
牛顿法既参考了一阶导数的信息,也参考了二阶导数的信息。在理解牛顿法之前,可以参考驻点以及二阶导对驻点的判断一文。
牛顿法先在某点进行二阶泰勒展开,用二次函数近似表示原函数。

然后求这个二次函数的驻点:
![]()
到
就是一次迭代。
如果原函数就是二次函数,那么牛顿法直接就找到了原函数驻点,停止迭代。如果原函数不是二次函数,那么需要使用二阶泰勒展开每次迭代到达近似二次函数的驻点,直至到达原函数驻点。
深度学习下的损失函数
在深度学习中,损失函数往往是高维的。
维度越高,最小值点出现的概率越来越低,鞍点出现的概率越来越高(呈指数级增大)。这和投硬币是一样的道理,在二维情况下,二阶导数矩阵的两个特征值都为正的概率(最小值点出现的概率)是1/4,在三维情况下,二阶导矩阵
的三个特征值都为正的概率(最小值点出现的概率)是1/8,等等......。在高维情况下,因为鞍点多,牛顿法有很大的概率会停在鞍点上。
并且在高维情况下,的特征值都为正的情况更有可能出现在损失函数低的地方,也就是说最小值点更有可能出现在损失函数低的地方,鞍点更有可能出现在损失函数高的地方。所以在高维情况下牛顿法不仅有很大的概率会停在鞍点上,并且这些鞍点还对应着较高的损失函数。
在高维的情况下,梯度下降法比牛顿法会取得更好的优化效果。因为梯度下降不断迭代寻找使得损失函数很低的点,而牛顿法不断迭代停留在某一驻点上(大概率是对应较高损失函数的鞍点)。
梯度下降法和牛顿法的对比
| 梯度下降法 | 牛顿法 | |
| 理念 | 不断迭代使损失函数下降,寻找损失函数值较低的点 | 不断迭代进行二阶泰勒近似,寻找驻点 |
| 优点 | 基本不会停留在鞍点 | 速度较快 |
| 缺点 | 速度较慢,需要选择合适的学习率 | 会停留在鞍点(损失函数较高) |
如果有不正确的地方,欢迎各位大佬留言呀~
相关文章:
梯度下降法和牛顿法
梯度下降法和牛顿法都是优化方法。 梯度下降法 梯度下降法和相关知识可以参考导数、偏导数、梯度、方向导数、梯度下降、二阶导数、二阶方向导数一文。梯度下降法是一种迭代地每次沿着与梯度相反方向前进的不断降低损失函数的优化方法。梯度下降只用到一阶导数的信息…...
elment-ui的侧边栏 开关及窗口联动
<template><div class"asders"><el-aside width"200px"><div class"boxbody"><div>源码外卖</div><el-switch v-model"isCollapse" :active-value"true" :inactive-value"fals…...

【从零开始学习JAVA | 第三十二篇】 异常(下)新手必学!
目录 前言: Exceptions(异常): 异常的两大作用: 异常的处理方式: 1.JVM默认处理 2.自己捕获异常 3.抛出处理 自定义异常: 异常的优点: 总结: 前言: 前…...

onnxruntime (C++/CUDA) 编译安装
一、克隆及编译 git clone --recursive https://github.com/Microsoft/onnxruntime cd onnxruntime/ git checkout v1.8.0如果克隆的时候报错: 执行以下: apt-get install gnutls-bin git config --global http.sslVerify false git config --global h…...

第三篇-Tesla P40+CentOS-7+CUDA 11.7 部署实践
第一篇-ChatGLM-webui-Windows安装部署-CPU版 第二篇-二手工作站配置 第三篇-Tesla P40CentOS-7CUDA 11.7 部署实践 硬件环境 系统:CentOS-7 CPU: 14C28T 显卡:Tesla P40 24G 准备安装 驱动: 515 CUDA: 11.7 cuDNN: 8.9.2.26 安装依赖 yum clean al…...
Unity游戏源码分享-ARPG游戏Darklight.rar
Unity游戏源码分享-ARPG游戏Darklight.rar 玩法 项目地址:https://download.csdn.net/download/Highning0007/88105464...

类型转换运算符
当我们想要将自定义类的对象转换为目标类型时,我们可以通过重载类型转换运算符(conversion operator)来实现。 以下是一个示例代码,展示了如何在 C 中定义一个自定义类,并重载类型转换运算符将对象转换为目标类型&…...

Kafka 入门到起飞系列 - 消费者组管理、位移管理
消费者组 - Consumer Group 上文我们已经讲过消费者组了,我们知道消费组的存在可以保证一个主题下一个分区的消息只会被组内一个消费者消费,从而避免了消息的重复消费 什么是消费组 - Consumer Group? 消费者组是Kafka 提供的可扩展且具有容…...

SpringBoot——数据层三组件之间的关系
简单介绍 在之前的文章中,我们介绍了一下SpringBoot中内置的几种数据层的解决方案,在数据层由三部分组成,分别是数据库,持久化技术以及数据源,但是我今天写着写着,突然就想不起来这三部分到底是干什么的了…...
LeetCode647.Palindromic-Substrings<回文子串>
题目: 思路: 错误代码:(缺少部分判断) 使用的是寻找回文子串的方法。以一个点为中心向两边扫描。但是有一点小问题。 因为回文子串是分奇偶的,所以需要两种判断方式。 看了下答案后发现我的代码距离答案一…...

React的hooks---useContext
Context 提供了一个无需为每层组件手动添加 props ,就能在组件树间进行数据传递的方法,useContext 用于函数组件中订阅上层 context 的变更,可以获取上层 context 传递的 value prop 值 useContext 接收一个 context 对象(React.…...
【Terraform学习】TerraformCloud入门介绍(快速入门)
TerraformCloud入门介绍 什么是 TerraformCloud? Terraform Cloud是Hashicorp Terraform的SaaS版本。 免费版功能 免费版功能包括版本控制集成、远程计划和实施远程计划和实施、通知及webhook、全http API驱动、状态管理、模拟计划、私有化模块注册器以及全HTTP界…...

linux实现运行java分包部署
1.打好包之后 找到bin文件夹下的 startup.sh文件 2.cd 进入bin文件夹下 3.执行 sh startup.sh 运行命令 4.如果出现此错误 是Windows和Linux的.sh脚本文件格式不同,如果在脚本中有空行,脚本是在Windows下进行编辑之后上传到linux上去执行的话,…...
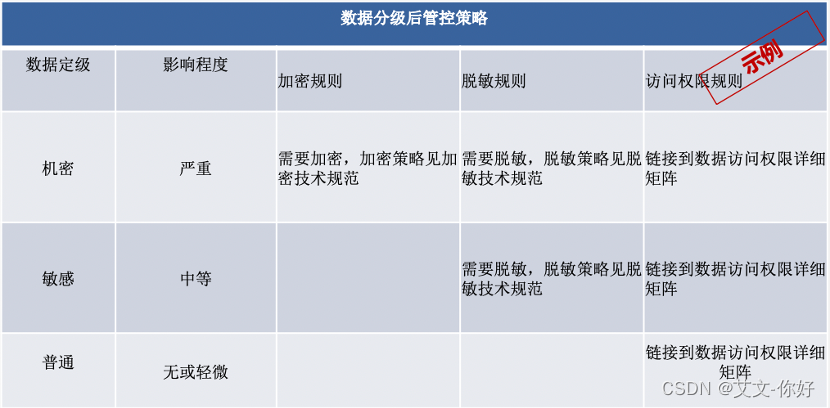
数据安全之全景图系列——数据分类分级落地实践
1、数据分类分级现状 我们正处于一个数据爆炸式增长的时代,随着产业数字化转型升级的推进,数据已被国家层面纳入生产要素,并且成为企业、社会和国家层面重要的战略资源。数据分类分级管理不仅是加强数据交换共享、提升数据资源价值的前提条件…...

C++实现MySQL数据库连接池
C实现MySQL数据库连接池 涉及技术 MySQL数据库编程、单例模式、STL容器、C11多线程(线程互斥、线程互斥、线程同步通信和unique_lock)、智能指针shared_ptr、lambda表达式、生产者-消费者线程模型。 项目背景 为了提升MySQL数据库(基于C/…...

day4 驱动开发 c语言学习
不利用系统提供的register_chrdev,自己实现字符设备的注册 底层代码 led.c #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include <linux/uaccess.h> #include <linux/io.h> #include "head.h…...
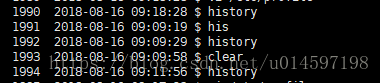
history命令:显示命令执行时间
1.修改配置文件 vim /etc/profile 添加内容 export HISTTIMEFORMAT"%Y-%m-%d %H:%M:%S " #注意:在末尾的“引号”与“S”之间,加入一位空格,将日期时间和历史命令用空格相隔开来。 你也可以换一种清晰的形式,效果…...

Django接口返回JSON格式数据报文
目录 遇到问题 Django返回json结构报文 不可行方式python json 可行方式JsonResponseQuerySet.values()。 python的两个web框架,flask和django,两者都具有view 模板的章节,但是当前开发一个应用,大部分采用前后端分离的合作方式。…...
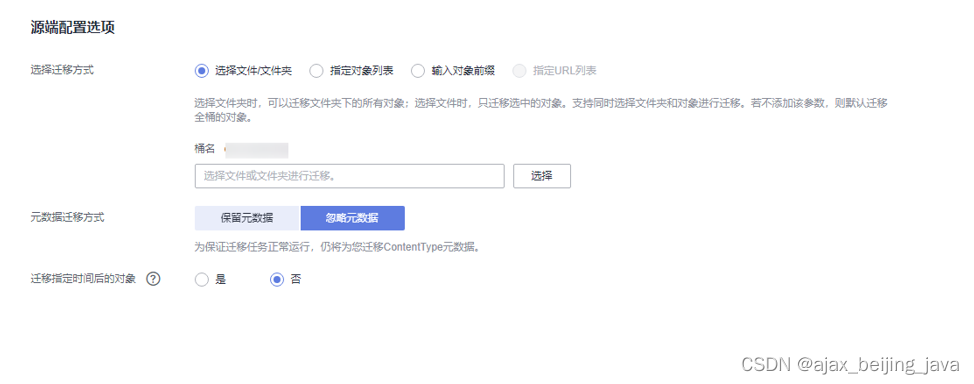
OBS 迁移--华为云
一、创建迁移i任务 1. 登录管理控制台。 2. 单击管理控制台左上角的 在下拉框中选择区域。 3. 单击“ 服务列表 ”,选择“ 迁移 > 对象存储迁移服务 OMS ”,进入“ 对象存储迁移服务 ”页面。 4. 单击页面右上角“ 创建迁移任务 ”。 5. 仔细阅读…...
【Docker consul的容器服务更新与发现】
文章目录 一、Consul 的简介(1)什么是服务注册与发现(2)什么是consul 二、consul 部署1、consul服务器1. 建立 Consul 服务2. 查看集群信息3. 通过 http api 获取集群信息 2、registrator服务器1. 安装 Gliderlabs/Registrator2. …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
