【T1】存货成本异常、数量为零金额不为零的处理方法。
【问题描述】
使用T1飞跃专业版的过程中,
由于业务问题或者是操作问题,
经常会遇到某个商品成本异常不准确,
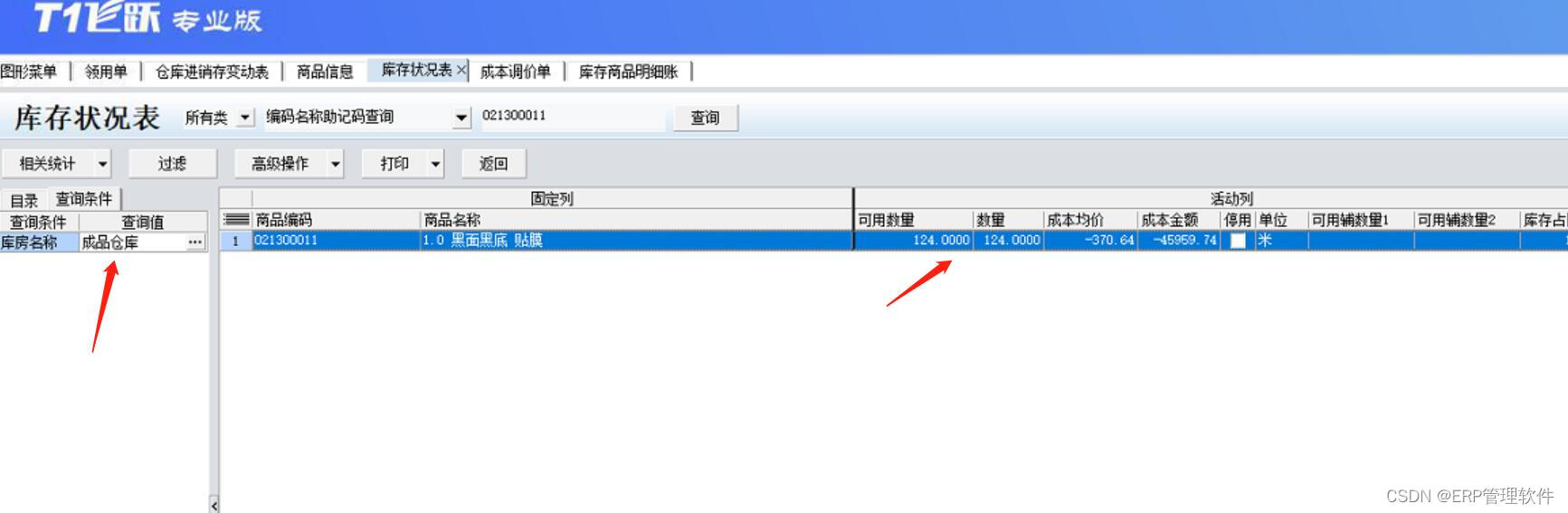
或者是遇到数量为0金额不为0的情况,需要将其成本调为0。
但是T1软件没有出入库调整单,并且结账无法针对数量为0金额不为0的商品,自动生成出库调整单。
【解决方法】
成本调整方法操作如下:
1、先在【业务单据】->【库存单据】下级菜单中点击【报溢单】,
录入商品后会自动弹出成本单价,录入报溢商品数量,此时录入数量应满足如下条件:
报溢单数量*成本单价>当前库存金额的绝对值
2、再次通过主菜单【业务单据】->【库存单据】->【调价单】功能录-<调价单>,
调整商品数量为当前仓库库存数,单价栏输入正确成本价。
3、然后录入-<报损单>(或<赠送单>)其商品数量等于原报溢数量过账后数据恢复正常。
相关文章:

【T1】存货成本异常、数量为零金额不为零的处理方法。
【问题描述】 使用T1飞跃专业版的过程中, 由于业务问题或者是操作问题, 经常会遇到某个商品成本异常不准确, 或者是遇到数量为0金额不为0的情况,需要将其成本调为0。 但是T1软件没有出入库调整单,并且结账无法针对数量…...
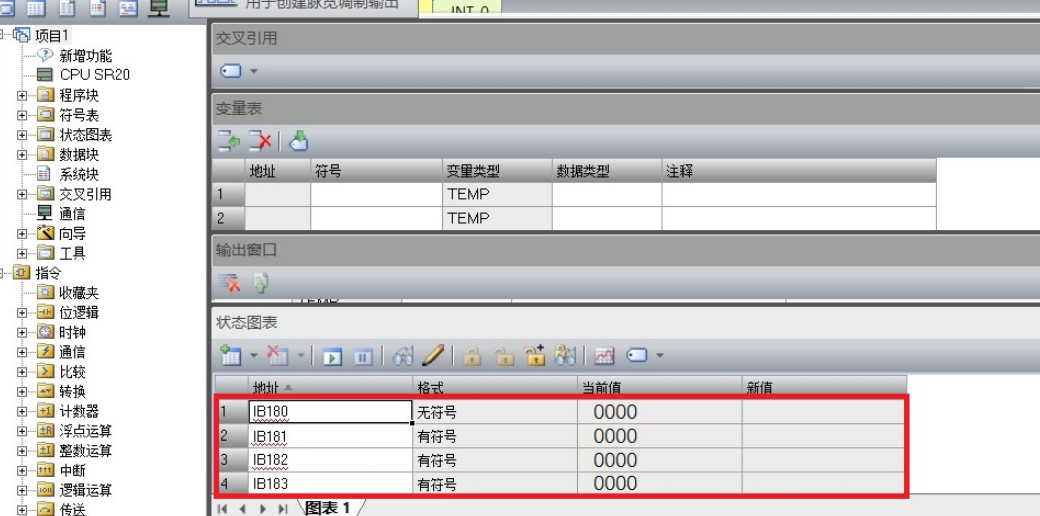
EtherNet IP转PROFINET网关连接西门子与欧姆龙方法
本文主要介绍了捷米特JM-PN-EIP(EtherNet/IP转PROFINET)网关西门子200智能PLC(PROFINET)和欧姆龙系统EtherNet/IP通信的配置过程。 1, 将 EDS 文件复制到欧姆龙软件的对应文件夹下 2, 首先添加捷米特JM-PN-EIP网关的全局变量&…...
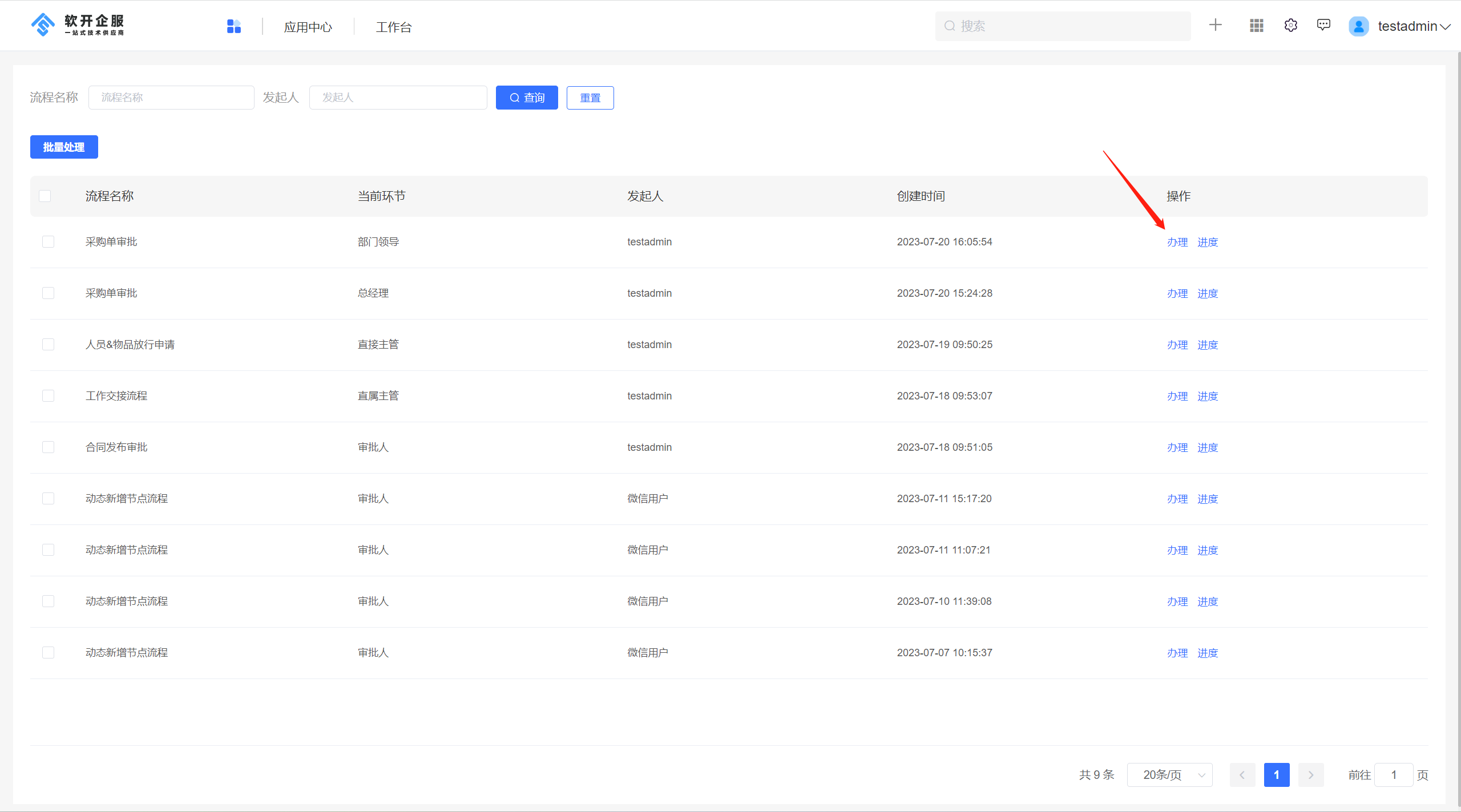
低代码开发重要工具:jvs-flow(流程引擎)审批功能配置说明
流程引擎场景介绍 流程引擎基于一组节点与执行界面,通过人机交互的形式自动地执行和协调各个任务和活动。它可以实现任务的分配、协作、路由和跟踪。通过流程引擎,组织能够实现业务流程的优化、标准化和自动化,提高工作效率和质量。 在企业…...

[SQL挖掘机] - GROUP BY语句
介绍: group by 是 sql 中用于对结果集进行分组的关键字。通过使用 group by,可以根据一个或多个列的值将结果集中的行分组,并对每个分组应用某种聚合函数(如 count、sum、avg 等)以生成汇总信息。这样可以方便地对数据进行分类、…...

【ubuntu|内核】ubuntu 22.04修改内核为指定版本
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 ubuntu 22.04 安装指定内核 1. 正文 查看已安装的内核镜像 dpkg --get-selections | grep linux-image1.1 安装指定版本的内核 安装镜像 sudo apt-g…...
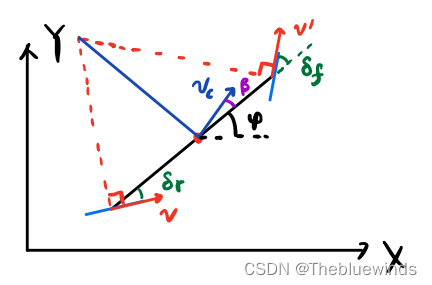
Carla教程一:动力学模型到LQR
Carla教程一、动力学模型到LQR 从运动学模型和动力学模型到LQR 模型就是可以描述车辆运动规律的模型。车辆建模都是基于自行车模型的设定,也就是将四个轮子抽象为自行车一样的两个轮子来建模。 1、运动学模型 运动学模型是基于几何关系分析出来的,一般适用于低俗情况下,…...
IDE/mingw下动态库(.dll和.a文件)的生成和部署使用(对比MSVC下.dll和.lib)
文章目录 概述问题的产生基于mingw的DLL动态库基于mingw的EXE可执行程序Makefile文件中使用Qt库的\*.a文件mingw下的*.a 文件 和 *.dll 到底谁起作用小插曲 mingw 生成的 \*.a文件到底是什么为啥mingw的dll可用以编译链接过程转换为lib引导文件 概述 本文介绍了 QtCreator mi…...
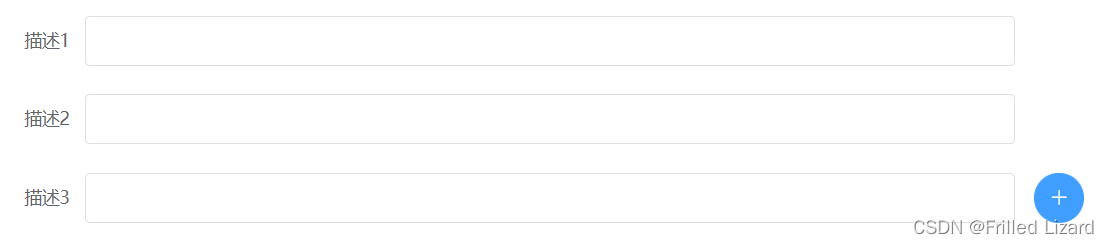
点击加号添加新的输入框
实现如上图的效果 html部分: <el-form-item class"forminput" v-for"(item,index) in formdata.description" :key"index" :label"描述(index1)" prop"description"><el-input v-model"formdata…...
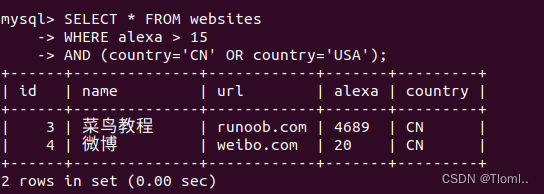
SQL AND OR 运算符
AND & OR 运算符用于基于一个以上的条件对记录进行过滤。 如果第一个条件和第二个条件都成立,则 AND 运算符显示一条记录。 如果第一个条件和第二个条件中只要有一个成立,则 OR 运算符显示一条记录。 下面是选自 "students" 表的数据&a…...

6、C++内存模型
原文: https://my.oschina.net/u/2516597/blog/805489 背景 C11开始支持多线程,其中提供了原子类型atomic, 和atomic关系比较密切的是memory_order,所有的内存模型都是指atomic类型 enum memory_order {memory_order_relaxed,memory_order…...
)
上海市青少年算法2023年1月月赛(丙组)
上海市青少年算法2023年1月月赛(丙组)T1 实验日志 题目描述 小爱正在完成一个物理实验,为期n天,其中第i天,小爱会记录ai条实验数据在实验日志中。 已知小爱的实验日志每一页最多纪录m条数据,每天做完实验后他都会将日志合上,第二天,他便从第一页开始依次翻页,直到找到…...
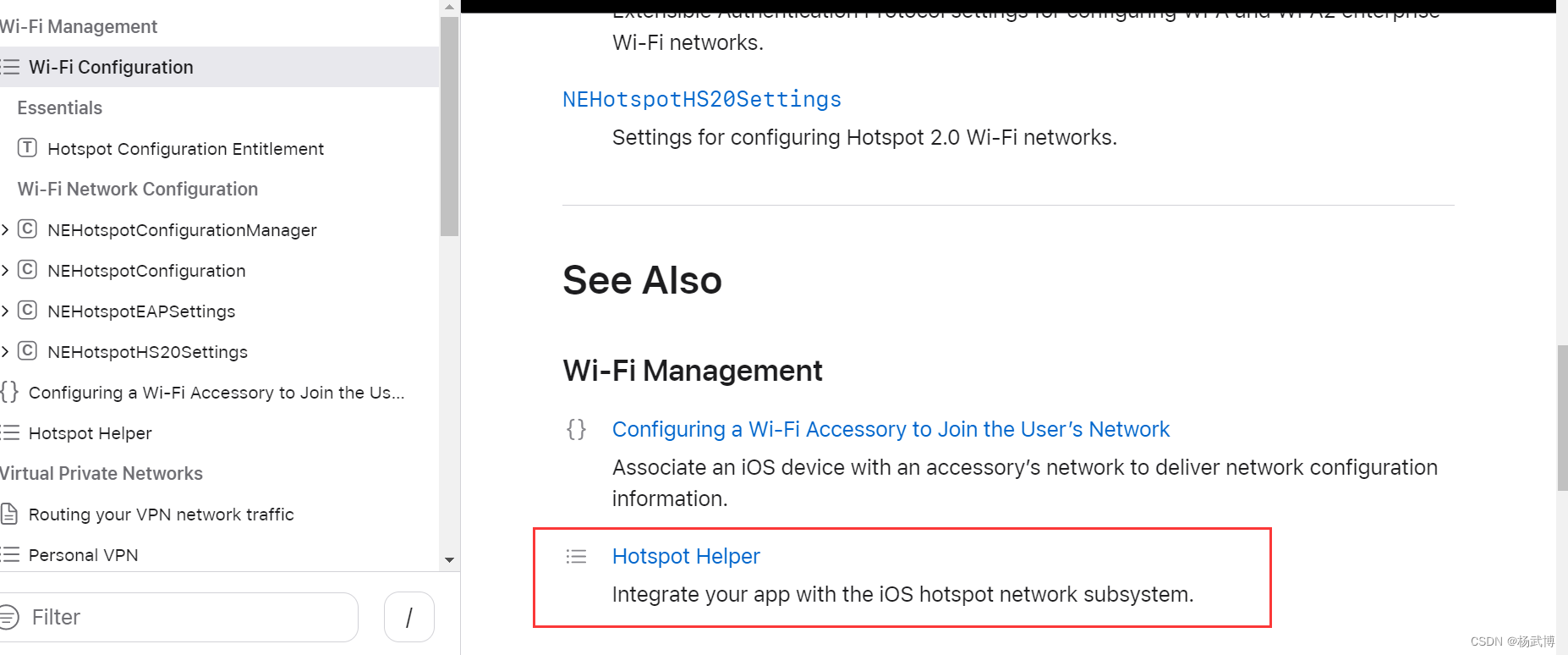
移动开发之Wifi列表获取功能
一、场景 业务需要通过App给设备配置无线网络连接,所以需要App获取附近的WiFi列表,并进行网络连接验证。 二、安卓端实现 1、阅读谷歌官网文档,关于Wifi 接口使用 https://developer.android.com/guide/topics/connectivity/wifi-scan?hl…...

MyBatisPlus - 实体类 的 常用注解
TableName(“表名”) 假设 表名是 book,实体类类名是 Book MyBatisPlus会进行自动映射 但如果 表名是 tab_book,实体类类名是 Book 那么MyBatisPlus就无法进行自动映射,需要我们使用 TableName注解 去指定实体类对应的表 如下 TableNa…...
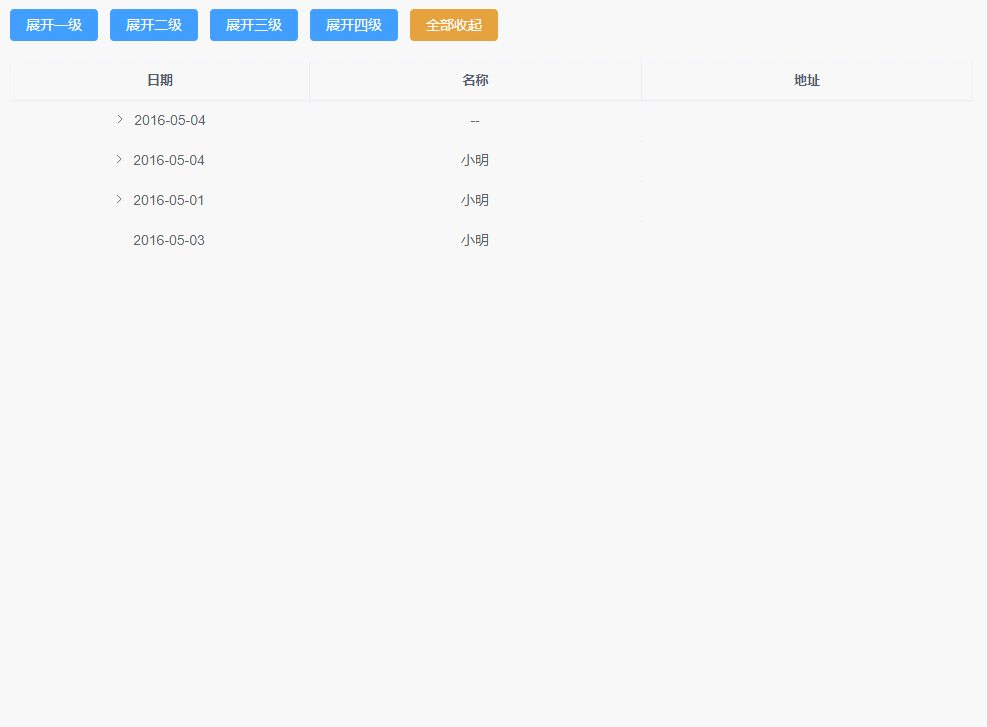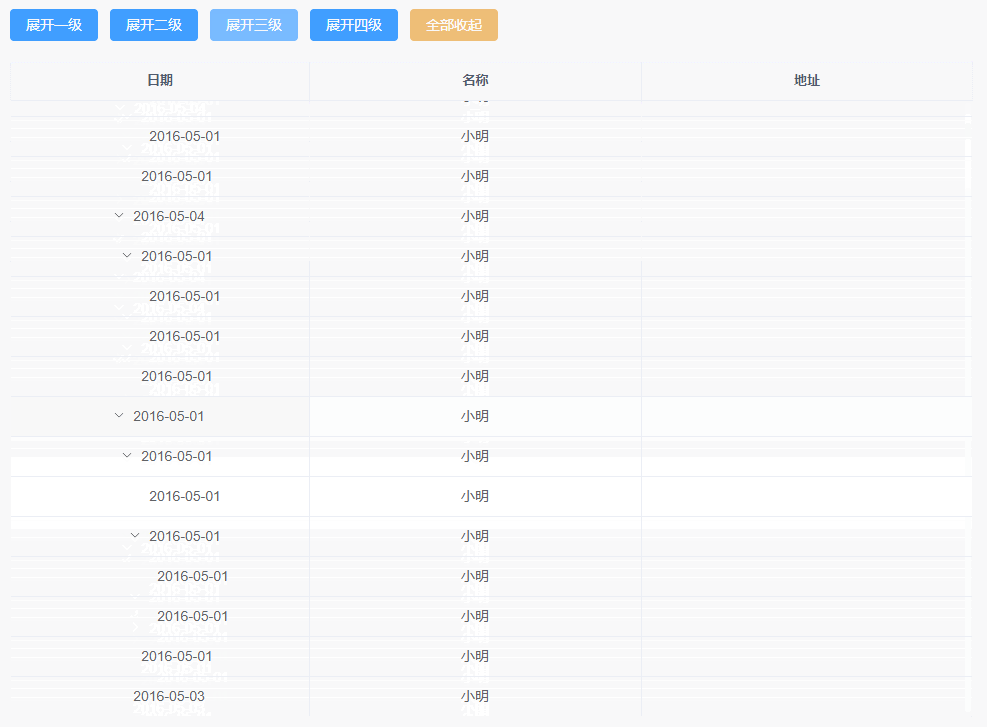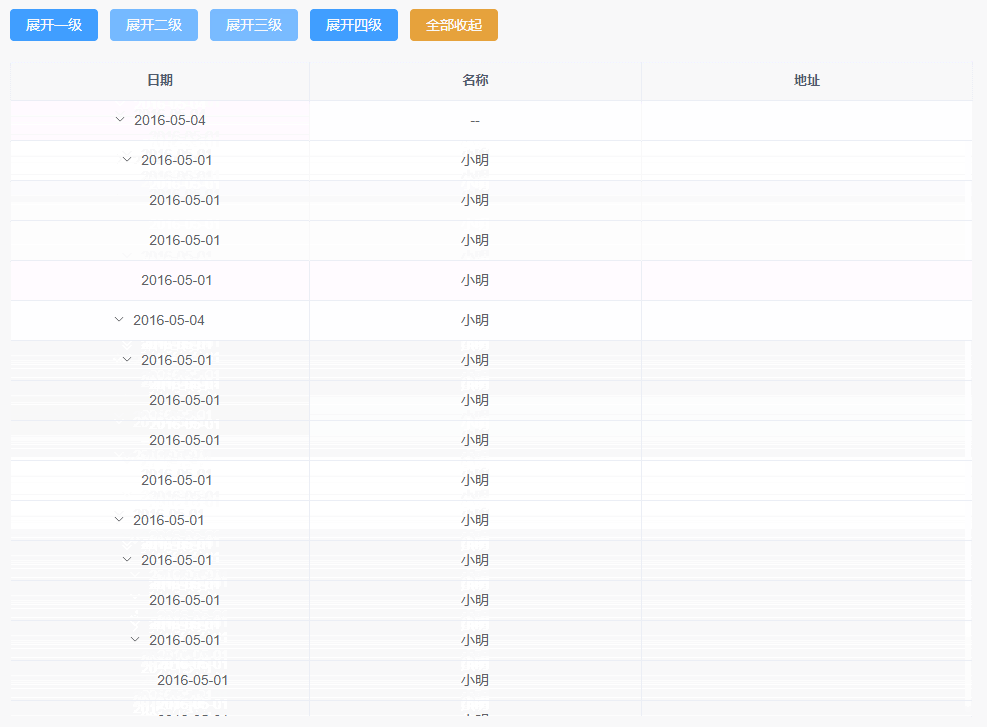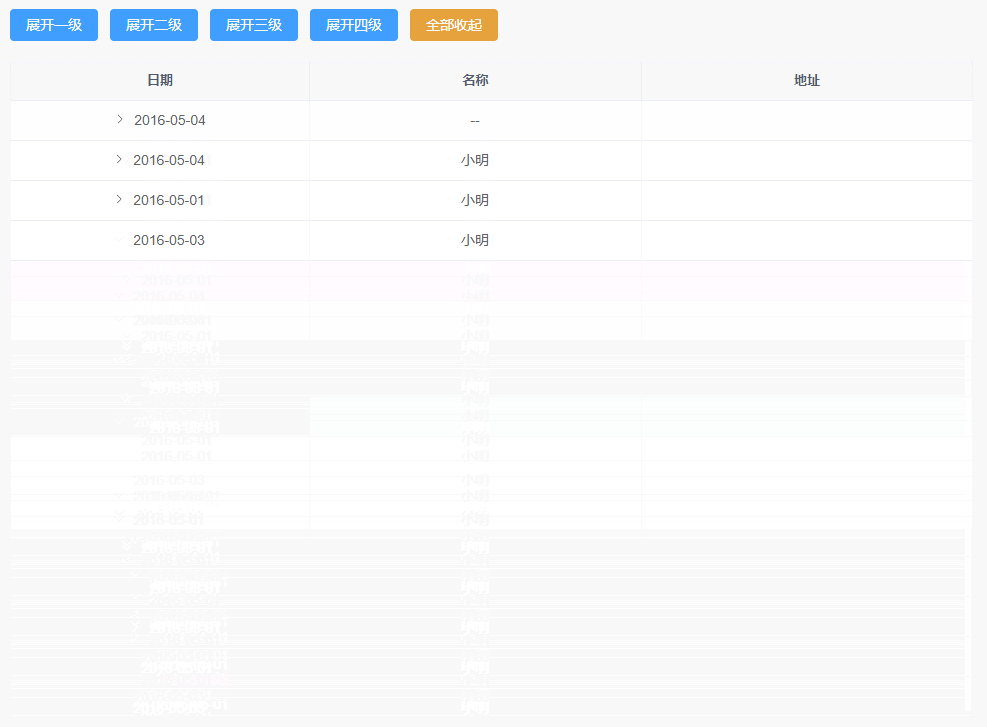
vue3+ts+elementui-plus二次封装树形表格实现不同层级展开收起的功能
一、TableTreeLevel组件 <template><div classmain><div class"btns"><el-button type"primary" click"expandLevel(1)">展开一级</el-button><el-button type"primary" click"expandLevel(2…...
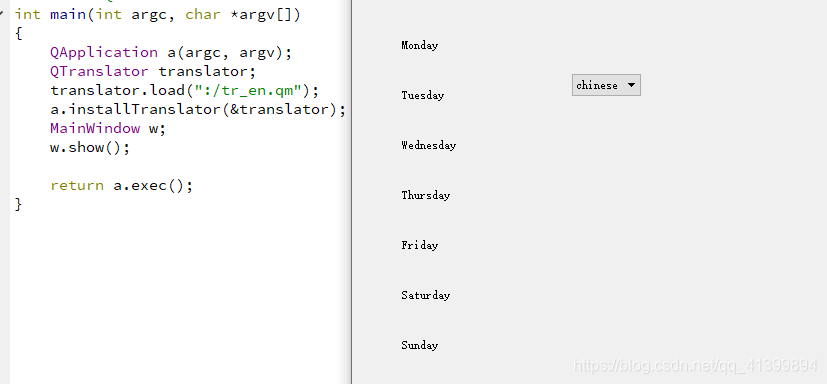
Qt之切换语言的方法(传统数组法与Qt语言家)
http://t.csdn.cn/BVigB 传统数组法: 定义一个字符串二维数组, QString weekStr[2][7] {"星期一","星期二","星期三","星期四","星期五","星期六","星期日",\ "Monday&…...

qt root start faild
深入解析chown -r root:root命令_笔记大全_设计学院 ffmpeg第五弹:QtSDLffmpeg视频播放演示_txp玩Linux的博客-CSDN博客...

数据结构—串
4.1串 4.1.1串的定义 串(String)——零个或多个任意字符组成的有限序列 S"a1 a2...an"串的定义——几个术语 子串:串中任意个连续字符组成的子序列称为该串的子串 例如,“abcde”的子串有: “ ”、“a”、…...

hive 全量表、增量表、快照表、切片表和拉链表
全量表:记录每天的所有的最新状态的数据,增量表:记录每天的新增数据,增量数据是上次导出之后的新数据。快照表:按日分区,记录截止数据日期的全量数据切片表:切片表根据基础表,往往只…...
数据结构07:查找[C++][B树Btree]
图源:文心一言 考研对于B树的要求重点在推理手算的部分,只参考王道论坛咸鱼老师的视频就可以了;若时间非常充裕的小伙伴,也可以往下滑了解一下代码~🥝🥝 备注: 这次的代码是从这里复制的&…...
)
在CSDN学Golang云原生(Kubernetes集群管理)
一,Node的隔离与恢复 在 Kubernetes 集群中,Node 的隔离与恢复通常可以通过以下方式实现: 使用 Taints 和 Tolerations 实现隔离 Taints 和 Tolerations 是 Kubernetes 中用于节点调度的机制。通过给节点添加 taints(污点&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
