Carla教程一:动力学模型到LQR
Carla教程一、动力学模型到LQR
从运动学模型和动力学模型到LQR
模型就是可以描述车辆运动规律的模型。车辆建模都是基于自行车模型的设定,也就是将四个轮子抽象为自行车一样的两个轮子来建模。
1、运动学模型
运动学模型是基于几何关系分析出来的,一般适用于低俗情况下,这种情况可以不考虑轮胎的侧偏特性。另外,这里假设前轮的方向就是当前车辆速度的方向。但是高速情况并非如此。整个控制量可以简化为加速度a和偏航角 δ \delta δ。其中油门代表a为正,刹车代表a为负。偏航角是方向盘的控制量。然后可以定义下面的几个状态量,用来描述车辆当前状态:
- x:车辆当前横轴坐标
- y:车辆纵轴坐标
- v: 车辆速度
- φ \varphi φ:车辆横摆角
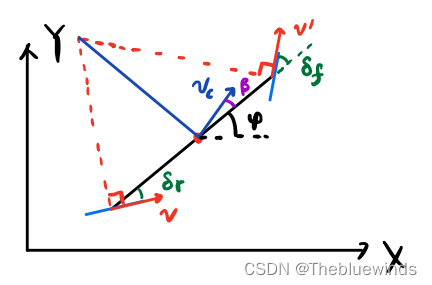
最后推导得到的动力学模型如下:
x ˙ = v cos φ y ˙ = v sin φ φ ˙ = v tan δ f L \dot{x}=v\cos \varphi \\ \dot{y}=v\sin \varphi \\ \dot{\varphi}=\frac{v\tan \delta _f}{L} x˙=vcosφy˙=vsinφφ˙=Lvtanδf
其中 δ f \delta_f δf是前轮的转向角。因为后轮一般都是不转向的,所以 δ r \delta_r δr是零。
2、动力学模型
需要考虑轮胎的侧偏性质。动力学模型是通过对轮胎和地面之间的相互作用来描述车辆的运动。动力学模型是基于车辆的动力学原理进行建模的,它考虑了车辆的质量、加速度、速度、转向等因素,可以更加精确地预测车辆的运动轨迹。动力学模型的优点在于可以考虑更多的因素,更加精确地预测车辆的运动轨迹,适用于高速行驶和紧急情况下的自动驾驶。但是,动力学模型对传感器的精度要求较高,对于复杂的路况和车辆之间的交互,需要更多的计算资源。
动力学模型可以将车辆运动的横纵向解耦,而运动学模型则无法解耦。
根据自行车动力学模型的推导,注意动力学模型中一个很关键的参数就是轮胎测偏参数,轮胎测偏力和轮胎测偏角度成正比。在实际中,测偏刚度是负数。
经过推导可以计算出关于横向速度和角速度作为状态变量,横向加速度和横向角速度变化量为因变量的状态方程。如下:
( y ¨ φ ¨ ) = ( C φ f + C φ r m v x a C φ f − b C φ r I v x a C φ f + b C φ r m v x − v x a 2 C φ f + b 2 C φ r I v x ) ( y ˙ φ ˙ ) + ( − C φ f m − a C φ f I ) δ \,\,\left( \begin{array}{c} \ddot{y}\\ \ddot{\varphi}\\ \end{array} \right) \,\,=\,\,\left( \begin{array}{c} \frac{C_{\varphi _f}+\,\,C_{\varphi _r}}{mv_x}\\ \frac{aC_{\varphi _f}-\,\,bC_{\varphi _r}}{Iv_x}\\ \end{array} \right. \left. \begin{array}{c} \frac{aC_{\varphi _f}+\,\,bC_{\varphi _r}}{mv_x}-v_x\\ \frac{a^2C_{\varphi _f}+\,\,b^2C_{\varphi _r}}{Iv_x}\\ \end{array} \right) \left( \left. \begin{array}{c} \dot{y}\\ \dot{\varphi}\\ \end{array} \right) \right. \,\,+\,\,\left( \begin{array}{c} -\frac{C_{\varphi _f}}{m}\\ -\frac{aC_{\varphi f}}{I}\\ \end{array} \right) \delta (y¨φ¨)=(mvxCφf+CφrIvxaCφf−bCφrmvxaCφf+bCφr−vxIvxa2Cφf+b2Cφr
相关文章:

Carla教程一:动力学模型到LQR
Carla教程一、动力学模型到LQR 从运动学模型和动力学模型到LQR 模型就是可以描述车辆运动规律的模型。车辆建模都是基于自行车模型的设定,也就是将四个轮子抽象为自行车一样的两个轮子来建模。 1、运动学模型 运动学模型是基于几何关系分析出来的,一般适用于低俗情况下,…...
IDE/mingw下动态库(.dll和.a文件)的生成和部署使用(对比MSVC下.dll和.lib)
文章目录 概述问题的产生基于mingw的DLL动态库基于mingw的EXE可执行程序Makefile文件中使用Qt库的\*.a文件mingw下的*.a 文件 和 *.dll 到底谁起作用小插曲 mingw 生成的 \*.a文件到底是什么为啥mingw的dll可用以编译链接过程转换为lib引导文件 概述 本文介绍了 QtCreator mi…...
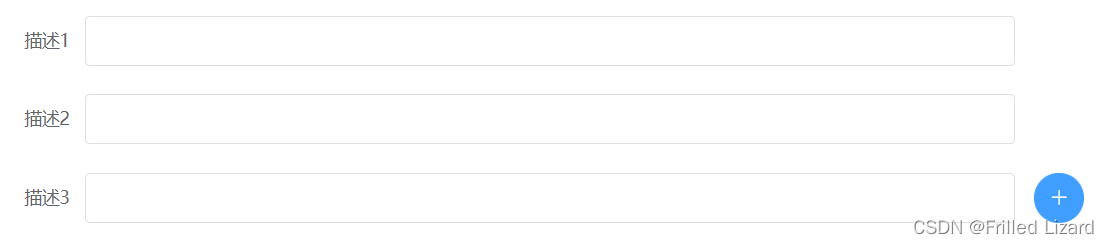
点击加号添加新的输入框
实现如上图的效果 html部分: <el-form-item class"forminput" v-for"(item,index) in formdata.description" :key"index" :label"描述(index1)" prop"description"><el-input v-model"formdata…...
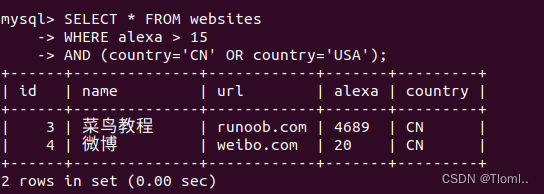
SQL AND OR 运算符
AND & OR 运算符用于基于一个以上的条件对记录进行过滤。 如果第一个条件和第二个条件都成立,则 AND 运算符显示一条记录。 如果第一个条件和第二个条件中只要有一个成立,则 OR 运算符显示一条记录。 下面是选自 "students" 表的数据&a…...

6、C++内存模型
原文: https://my.oschina.net/u/2516597/blog/805489 背景 C11开始支持多线程,其中提供了原子类型atomic, 和atomic关系比较密切的是memory_order,所有的内存模型都是指atomic类型 enum memory_order {memory_order_relaxed,memory_order…...
)
上海市青少年算法2023年1月月赛(丙组)
上海市青少年算法2023年1月月赛(丙组)T1 实验日志 题目描述 小爱正在完成一个物理实验,为期n天,其中第i天,小爱会记录ai条实验数据在实验日志中。 已知小爱的实验日志每一页最多纪录m条数据,每天做完实验后他都会将日志合上,第二天,他便从第一页开始依次翻页,直到找到…...
移动开发之Wifi列表获取功能
一、场景 业务需要通过App给设备配置无线网络连接,所以需要App获取附近的WiFi列表,并进行网络连接验证。 二、安卓端实现 1、阅读谷歌官网文档,关于Wifi 接口使用 https://developer.android.com/guide/topics/connectivity/wifi-scan?hl…...

MyBatisPlus - 实体类 的 常用注解
TableName(“表名”) 假设 表名是 book,实体类类名是 Book MyBatisPlus会进行自动映射 但如果 表名是 tab_book,实体类类名是 Book 那么MyBatisPlus就无法进行自动映射,需要我们使用 TableName注解 去指定实体类对应的表 如下 TableNa…...
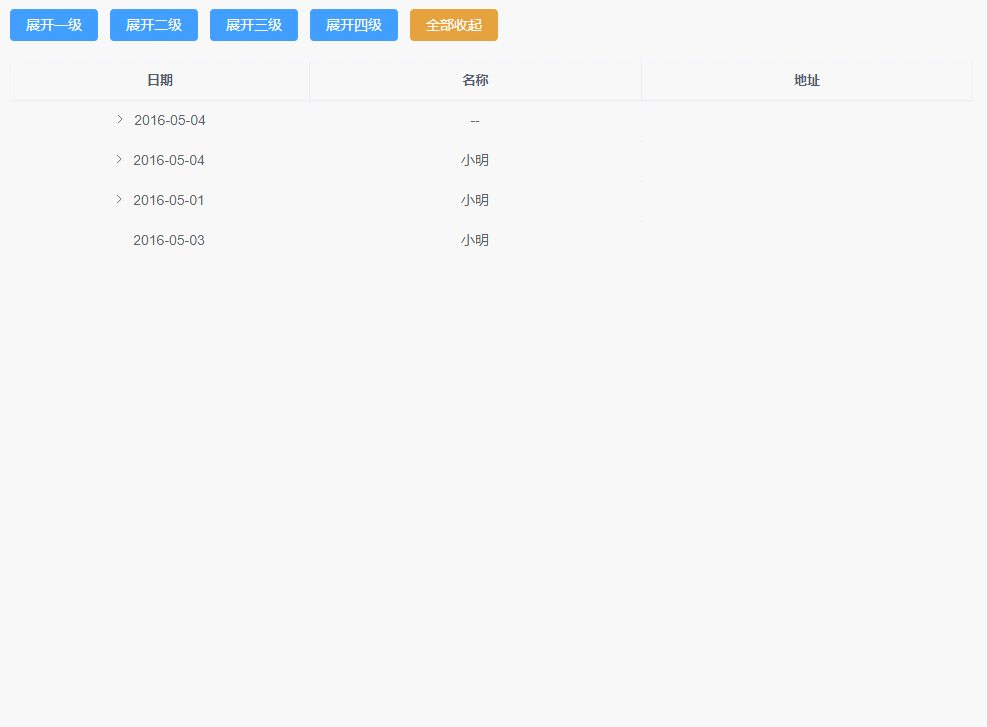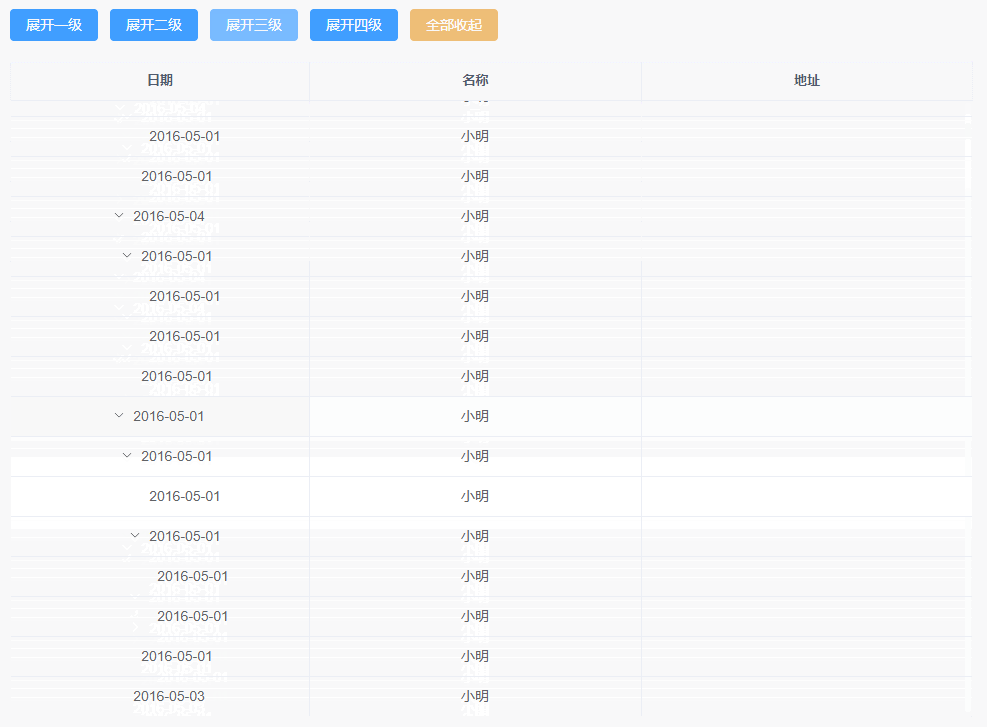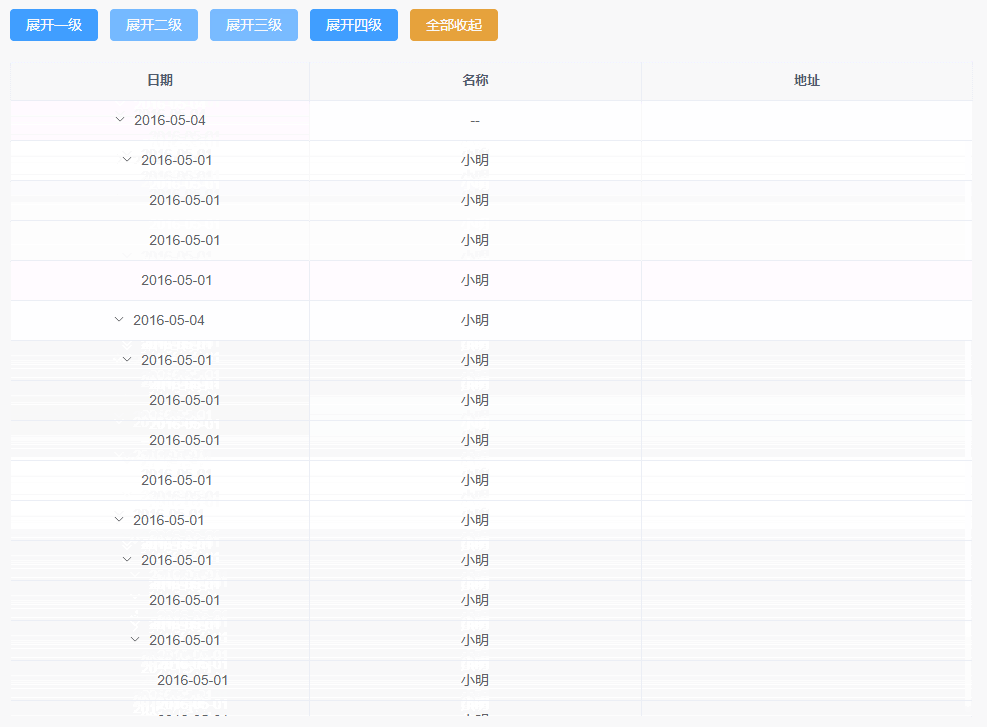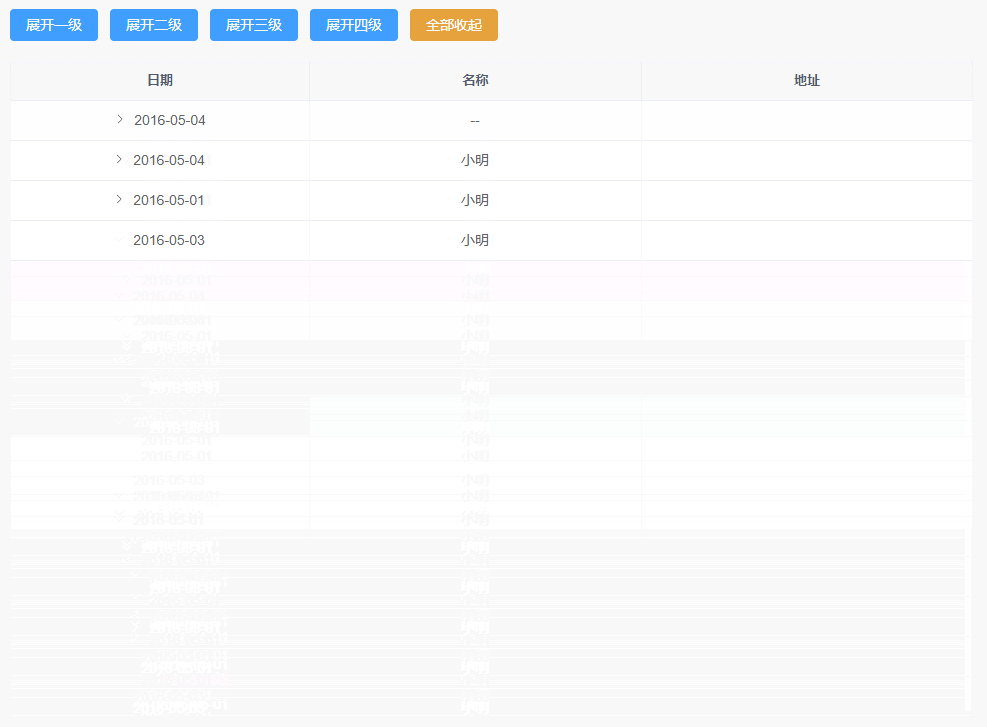
vue3+ts+elementui-plus二次封装树形表格实现不同层级展开收起的功能
一、TableTreeLevel组件 <template><div classmain><div class"btns"><el-button type"primary" click"expandLevel(1)">展开一级</el-button><el-button type"primary" click"expandLevel(2…...
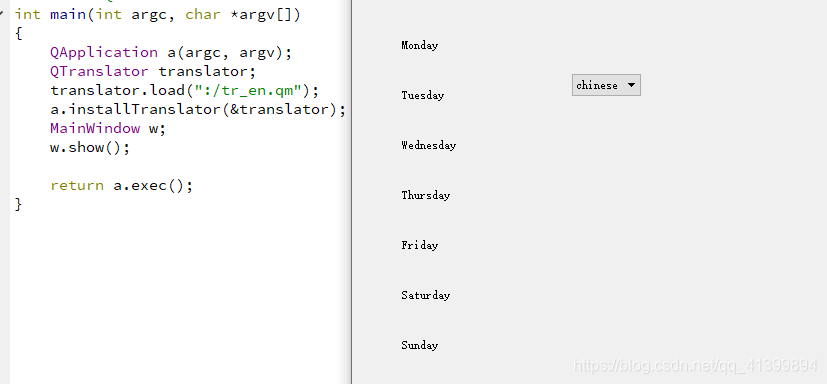
Qt之切换语言的方法(传统数组法与Qt语言家)
http://t.csdn.cn/BVigB 传统数组法: 定义一个字符串二维数组, QString weekStr[2][7] {"星期一","星期二","星期三","星期四","星期五","星期六","星期日",\ "Monday&…...

qt root start faild
深入解析chown -r root:root命令_笔记大全_设计学院 ffmpeg第五弹:QtSDLffmpeg视频播放演示_txp玩Linux的博客-CSDN博客...

数据结构—串
4.1串 4.1.1串的定义 串(String)——零个或多个任意字符组成的有限序列 S"a1 a2...an"串的定义——几个术语 子串:串中任意个连续字符组成的子序列称为该串的子串 例如,“abcde”的子串有: “ ”、“a”、…...

hive 全量表、增量表、快照表、切片表和拉链表
全量表:记录每天的所有的最新状态的数据,增量表:记录每天的新增数据,增量数据是上次导出之后的新数据。快照表:按日分区,记录截止数据日期的全量数据切片表:切片表根据基础表,往往只…...
数据结构07:查找[C++][B树Btree]
图源:文心一言 考研对于B树的要求重点在推理手算的部分,只参考王道论坛咸鱼老师的视频就可以了;若时间非常充裕的小伙伴,也可以往下滑了解一下代码~🥝🥝 备注: 这次的代码是从这里复制的&…...
)
在CSDN学Golang云原生(Kubernetes集群管理)
一,Node的隔离与恢复 在 Kubernetes 集群中,Node 的隔离与恢复通常可以通过以下方式实现: 使用 Taints 和 Tolerations 实现隔离 Taints 和 Tolerations 是 Kubernetes 中用于节点调度的机制。通过给节点添加 taints(污点&…...

WPF实战学习笔记18-优化设计TodoView
文章目录 优化设计TodoView修复新增项目无法编辑问题增加了对完成状态的区分增加了选项卡删除功能更新删除请求URI添加删除命令并初始化UI添加删除按钮更改控制器 增加查询结果为空的图片增加转换器修改UI添加资源、命名空间 添加相关元素 增加了根据状态查询的功能Mytodo.Serv…...

Python版day59
503. 下一个更大元素 II 给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。 数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数&…...

[SQL挖掘机] - 算术运算符
在 sql 中,算术运算符主要用于执行数值计算操作,并且在查询语句中具有重要的地位。下面是算术运算符在 sql 中的一些作用和地位: 进行数值计算:算术运算符可以对数值类型的数据进行加减乘除等数值计算操作。例如,可以…...

机器学习基础 数据集、特征工程、特征预处理、特征选择 7.27
机器学习基础 1. 数据集 2. 特征工程 3. 学习分类 4. 模型 5. 损失函数 6. 优化 7. 过拟合 8. 欠拟合数据集 又称资料集、数据集合或者资料集合,是一种由数据所组成的集合特征工程 1. 特征需求 2. 特征设计 3. 特征处理特征预处理、特征选择、特征降维 4. 特征验…...

Sass 常用的功能!
Sass 常用功能 Sass 功能有很多,这边只列举一些比较常用的。 嵌套规则 (Nested Rules) Sass 允许将一套 CSS 样式嵌套进另一套样式中,内层的样式将它外层的选择器作为父选择器。 编译前 .box {.box1 {background-color: red;}.box2 {background-col…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
