1300*B. T-primes

解析:
有且只有三个因数,当且仅当,完全平方数并且sqrt(n)为素数
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
ll t,n;
bool prime(ll x){if(x<2) return 0;for(int i=2;i<=x/i;i++) if(x%i==0) return 0;return 1;
}
bool f(ll x){if(x==1) return 0;ll s=sqrt(x);return s*s==x&&prime(s);
}
int main(){scanf("%lld",&t);while(t--){scanf("%lld",&n);if(f(n)) puts("YES");else puts("NO");}return 0;
}相关文章:

1300*B. T-primes
解析: 有且只有三个因数,当且仅当,完全平方数并且sqrt(n)为素数 #include<bits/stdc.h> using namespace std; typedef long long ll; const int N1e55; ll t,n; bool prime(ll x){if(x<2) return 0;for(int…...

重新C++系列之运算符重载
一、什么是运算符重载 简单来讲就是对运算符赋予新的意义,但是又不能改变原有的含义,它本身也就是一个函数。运算符重载的本质是以函数的方式来体现。 二、运算符重载有几种 1、按照作用域来划分,有全局操作符重载函数和成员函数操作符重载函…...

kotlin异常处理try-catch-finally
kotlin异常处理try-catch-finally fun main(args: Array<String>) {try {println("a")} catch (e: Exception) {//异常捕获println("a-catch: $e")} finally {//善后,无论是否异常,都会执行println("a-finally")}t…...

Pytorch在cuda、AMD DirectML和AMD CPU下性能比较
一、测试环境 CUDA环境: i7-8550u 16G DDR4 2133MHz nVidia MX150 2GB AMD DirectML环境: Ryzen 5 5600G 32G DDR4 3200MHz Vega7 4GB AMD 纯CPU环境:Ryzen 5 5600G 32G DDR4 3200MHz 其他硬件配置的硬盘、电源均一致。Pytorch版本为2.0.0,Pyt…...

哈工大计算机网络课程局域网详解之:交换机概念
哈工大计算机网络课程局域网详解之:交换机概念 文章目录 哈工大计算机网络课程局域网详解之:交换机概念以太网交换机(switch)交换机:多端口间同时传输交换机转发表:交换表交换机:自学习交换机互…...

Jenkins Pipeline的hasProperty函数
函数的作用 用于判断某个参数或者字段是否存在。 用法 例子一 def projectStr "P1,P2,P3" pipeline {agent anyparameters {extendedChoice(defaultValue: "${projectStr}",description: 选择要发布的项目,multiSelectDelimiter: ,,name: SELECT_PROJ…...

芯片制造详解.净洁室的秘密.学习笔记(三)
这是芯片制造系列的第三期跟学up主三圈,这里对其视频内容做了一下整理和归纳,喜欢的可以看原视频。 芯片制造详解03: 洁净室的秘密|为何芯片厂缺人? 芯片制造详解.净洁室的秘密.学习笔记 三 简介一、干净的级别二、芯片…...
可解释的 AI:在transformer中可视化注意力
Visualizing Attention in Transformers | Generative AI (medium.com) 一、说明 在本文中,我们将探讨可视化变压器架构核心区别特征的最流行的工具之一:注意力机制。继续阅读以了解有关BertViz的更多信息,以及如何将此注意力可视化工具整合到…...

k8s Webhook 使用java springboot实现webhook 学习总结
k8s Webhook 使用java springboot实现webhook 学习总结 大纲 基础概念准入控制器(Admission Controllers)ValidatingWebhookConfiguration 与 MutatingWebhookConfiguration准入检查(AdmissionReview)使用Springboot实现k8s-Web…...
JS逆向之猿人学爬虫第20题-wasm
文章目录 题目地址sign参数分析python算法还原往期逆向文章推荐题目地址 https://match.yuanrenxue.cn/match/20第20题被置顶到了第1页,题目难度 写的是中等 算法很简单,就一个标准的md5算法,主要是盐值不确定, 而盐值就在wasm里面,可以说难点就在于wasm分析 sign参数分…...

【双指针优化DP】The 2022 Hangzhou Normal U Summer Trials H
Problem - H - Codeforces 题意: 思路: 首先很明显是DP 因为只有1e6个站点,因此可以以站点作为阶段 注意到K很小,因此可以尝试把这个当作第二维 设dp[i][j]为到达第i个站点,已经花了j元钱的最小步数 然后就想了一…...

[论文笔记] LLM数据集——金融数据集
一、chatglm_金融 ModelScope 魔搭社区 请将modelscope sdk升级到v1.7.2rc0,执行: pip3 install "modelscope1.7.2rc0" -f https://modelscope.oss-cn-beijing.aliyuncs.com/releases/repo.html # 方式1 git clone http://www.modelscope…...

在亚马逊平台,如何有效举报违规行为?
众所周知,在每个行业都有一些违规现象,甚至这些违规现象还会给自己带来利益方面的损失,一旦触犯到自己的利益的话,那自己是需要想办法解决的,想办法规避。 就拿开亚马逊店铺来说,比较容易遇到的就是产品侵…...

深度学习入门教学——神经网络
深度学习就是训练神经网络。 1、神经网络 举个最简单的例子,以下是一个使用线性回归来预测房屋价格的函数。这样一个用于预测房屋价格的函数被称作是一单个神经元。大一点的神经网络,就是将这些单个神经元叠加起来。例如:神经网络根据多个相…...

阿里Java开发手册~OOP 规约
1. 【强制】避免通过一个类的对象引用访问此类的静态变量或静态方法,无谓增加编译器解析成 本,直接用 类名 来访问即可。 2. 【强制】所有的覆写方法,必须加 Override 注解。 说明: getObject() 与 get 0 bject() 的问题。…...

【Mysql数据库面试01】内连接 左连接 右连接 全连接
【Mysql数据库】内连接 左连接 右连接 全连接 0.准备1.内连接1.1 SQL(不带where)1.2 SQL(带where)1.3总结 2.左连接2.1SQL(不带where)2.2SQL(带where)2.3总结 3.右连接3.1 SQL(不带where&#x…...
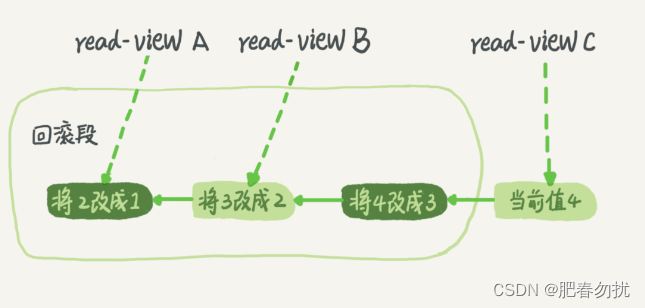
事务隔离:为什么你改了我还看不见
前提概要 你肯定不陌生,和数据库打交道的时候,我们总是会用到事务。最经典的例子就 是转账,你要给朋友小王转 100 块钱,而此时你的银行卡只有 100 块钱。 转账过程具体到程序里会有一系列的操作,比如查询余额、做加减法…...
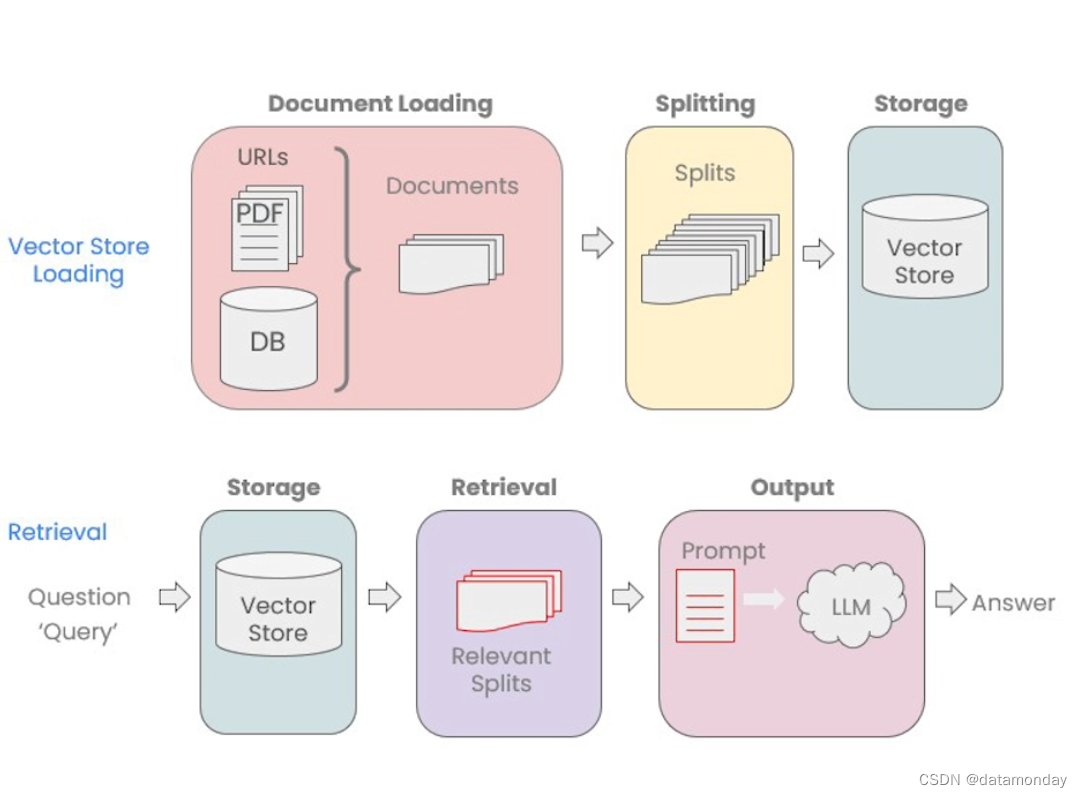
吴恩达ChatGPT《LangChain Chat with Your Data》笔记
文章目录 1. Introduction2. Document Loading2.1 Retrieval Augmented Generation(RAG)2.2 Load PDFs2.3 Load YouTube2.4 Load URLs2.5 Load Notion 3. Document Splitting3.1 Splitter Flow3.2 Character Splitter3.3 Token Splitter3.4 Markdown Spl…...

https和http有什么区别
https和http有什么区别 简要 区别如下: https的端口是443.而http的端口是80,且二者连接方式不同;http传输时明文,而https是用ssl进行加密的,https的安全性更高;https是需要申请证书的,而h…...
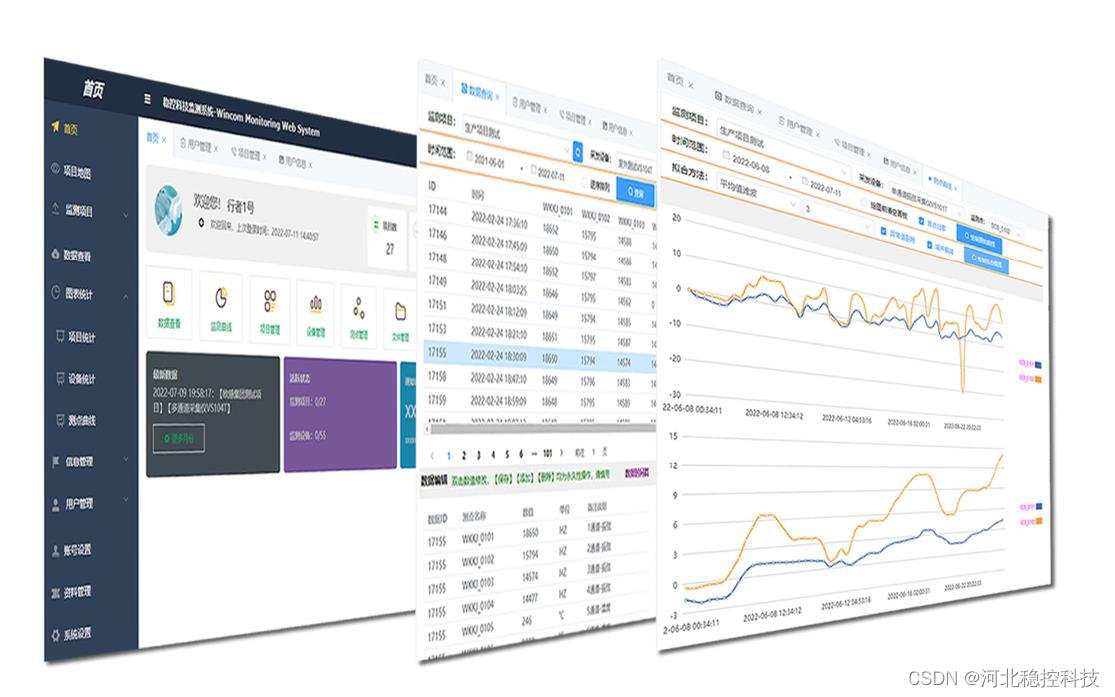
振弦采集仪及在线监测系统完整链条的岩土工程隧道安全监测
振弦采集仪及在线监测系统完整链条的岩土工程隧道安全监测 近年来,随着城市化的不断推进和基础设施建设的不断发展,隧道建设也日益成为城市交通发展的必需品。然而,隧道建设中存在着一定的安全隐患,如地质灾害、地下水涌流等&…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
