数据结构---并查集
目录标题
- 为什么会有并查集
- 并查集的原理
- 模拟实现并查集
- 准备工作
- 构造函数
- FindRoot
- Union
- SetCount
- 并查集实战
- 题目一:省份数量
- 题目解析
- 题目二:等式方程的可满足性
- 题目解析
为什么会有并查集
这里可以使用生活中的一个例子来带着大家理解并查集,大家在上学的过程中肯定会发现一种现象,在开学之前大家谁也不认识谁每个人都是一个小团体,可是开学之后因为座位旁边有一个同桌,所以开学没多久你和同桌就会互相认识并且开心的玩在一起,那么这时就是两个一个人的小团体融合成为了一个两个人的小团体,后来你可能会经常把头朝向后面看从而认识了你后面的人,经过了解之后你又跟你后桌的人相互认识从而带着你的同桌和他们玩在一起,那么这个时候两个两人的小团体就会融合成为一个4人的小团体,随着时间的流逝,不同人数的团体相互融合,最终一个班级的人从每个人都是一个小团体变成了一个所有人在一起成为一个大团体,那么为了描述不同团体进行融合的过程就有了查并集这个数据结构。
并查集的原理
我们先来看看并查集的比较官方的定义:在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。并查集是一个森林,所谓的森林就是指由多个树组成,比如说某公司今年校招全国总共招生10人,西安招4人,成都招3人,武汉招3人,10个人来自不同的学校,起先互不相识,每个学生都是一个独立的小团体,现给这些学生进行编号:{0, 1, 2, 3,4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体,数组中数字的绝对值代表:该小集体中具有成员的个数,那么这个数组就如下:

毕业后学生们要去公司上班,每个地方的学生自发组织成小分队一起上路,那么这个时候他们由一个人一个团体合并成为多个人一个团体,于是西安学生小分队s1={0,6,7,8},成都学生小分队s2={1,4,9},武汉学生小分队s3={2,3,5},10个人形成了三个小团体。假设右三个0,1,2担任队长,那么当前的结构就应该变成下面这样:
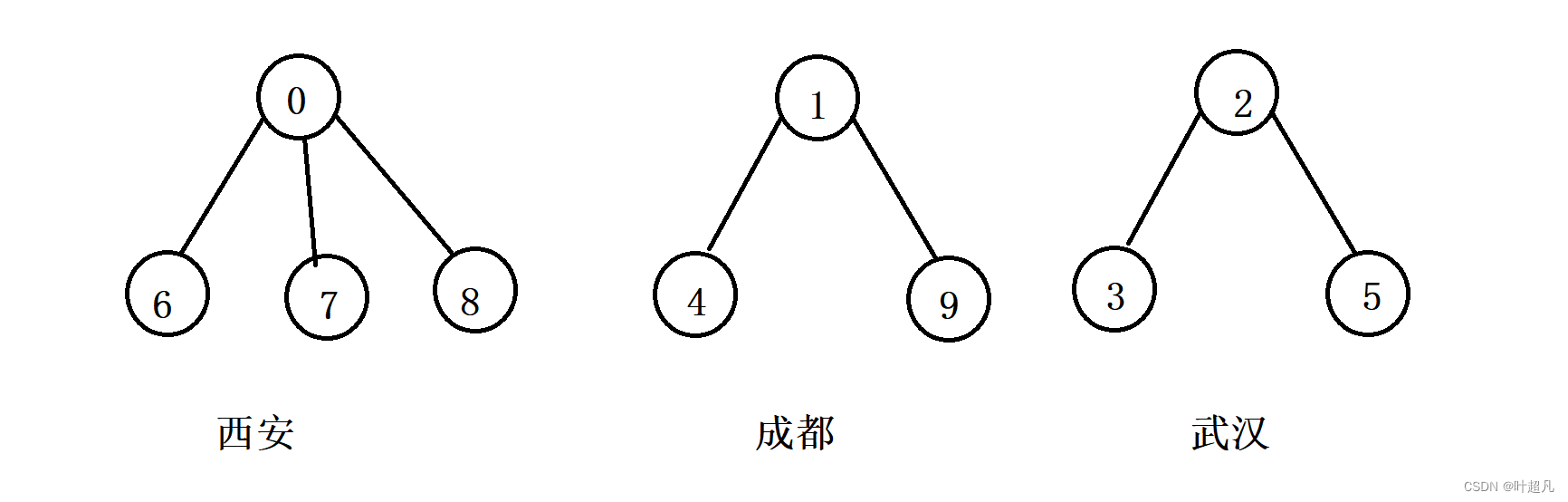
三个团体就是三个树,这三个树再构成一个森林,那么这里就有个问题我们如何把这三个树组合成为一个森林呢?答案是使用数组来对这些树进行合并,数组的下标对应着元素,下标对应的值就表示着不同元素之间的关系,如果你是根节点那么你下标对应的值就表示你这个树里面的节点个数,如果你是子树根节点或者子节点的话,那么你下标对应的值就是你父节点在数组中所在的位置,比如说元素0是西安这个树的根节点,元素0对应在数组中的下标为0,那么下标0中记录的数据就为-4表示西安这个树里面有4个节点,再比如说元素5对应的下标是5,那么在数组中下标5里面记录的数据就是2,表示当前的节点为子节点该节点的父节点在数组中的位置为5,那么其他节点也是依次类推,所以上面的数组就会变成下面这个样子:

知道了如何表示多棵树之后我们就来看看如何将两个树合并成为一棵树,比如说将上面的西安和成都进行合并那么我们就可以通过修改成都树中根节点的父节点,让其指向西安树的根节点来实现,那么这里的图片就变成下面这样:
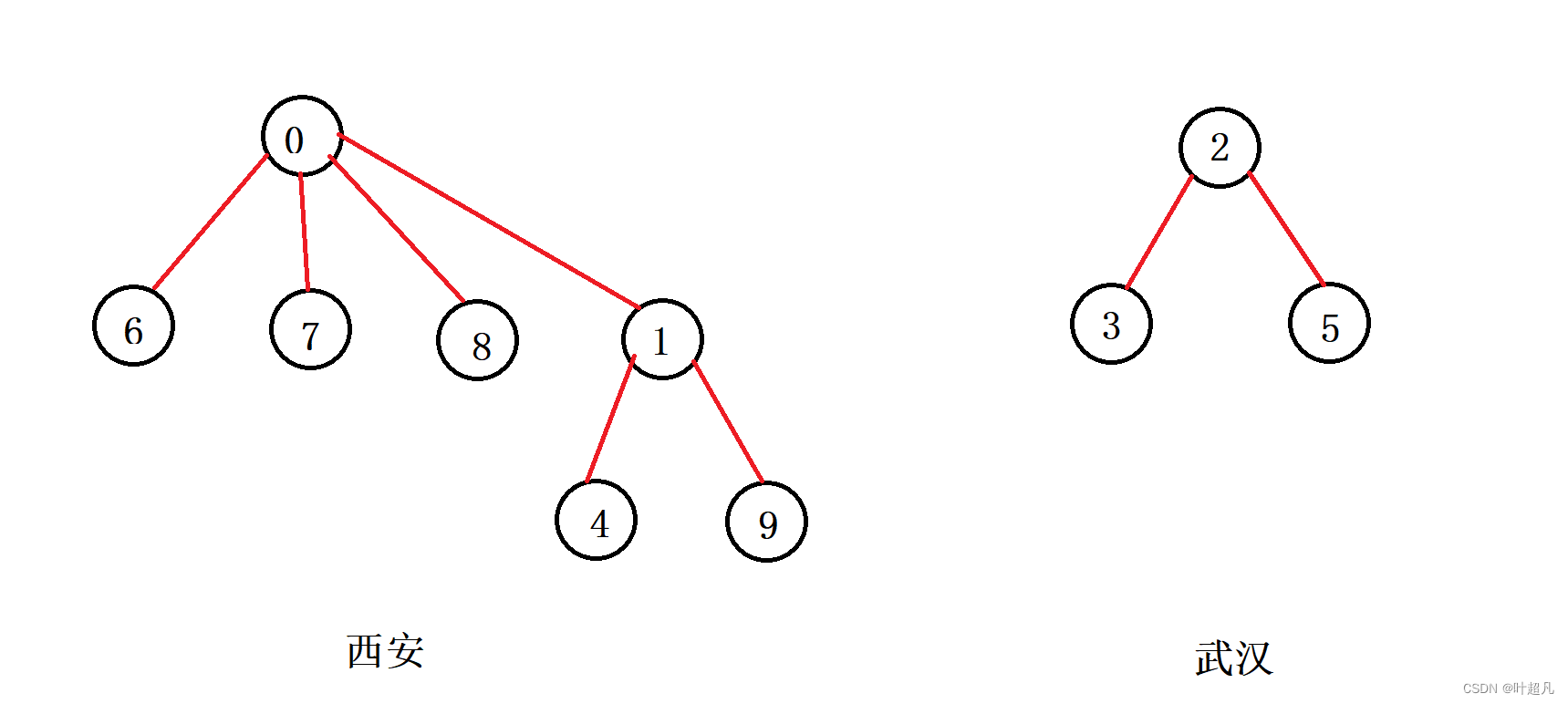
然后在数组中我们就得修改两个树的根节点所对应下标的值,首先将下标为1的值修改成为0表示节点1的父节点为0,将下标为0的值修改成为-7因为融合了一个新的树所以当前树中节点的个数就变多了,那么当前吧数组中的内容就变成下面这样,红色背景表示不同树的根节点,红色从原来的3个变成了2个,那么这就说名当前的森林只有两个树

知道了森林的表示方法和树融合的原理之后我们就可以来模拟实现并查集。
模拟实现并查集
准备工作
首先类里面得存在一个整型数组用来表示每个元素之间的关系:
class UnionFindSet
{
public:private:vector<int> _ufs;//用来表示元素之间的关系
};
但是这样做就会存在一个问题:我们怎么知道数组中的下标对应的是哪个元素呢?所以我们还得创建一个vector容器来方便我们查找下标所对应的元素,又因为元素可以是各种类型所以这里我们得添加一个类模板,模板中存在一个参数表示当前并查集处理的是哪种类型数据的关系,有了这个容器之后我们可以查看下标所对应的元素,那如果我们想查看元素对应的下标又该如何解决呢?所以我们还得创建一个map容器来记录每个元素所对应的下标,那么当前的代码就成为了下面这样:
template<class T>
class UnionFindSet
{
public:private:vector<int> _ufs;//用来表示元素之间的关系vector<T> _a;//根据下标找元素map<pair<T, int>> _indexmap;//根据元素找到下标
};
构造函数
构造函数需要两个参数,一个参数接收当前容器需要处理的数据数组,另外一个参数表示当前处理的数据个数:
UnionFindSet(const T* sorce, size_t num)
{}
然后我们就创建一个循环,在循环里面分别取参数数组的值将其插入到数组_a里面,因为循环是从0开始并且数组_a也是从下标为0的位置开始插入,所以在循环里面我们可以顺便往_indexmap容器种插入数据,那么这里的代码就如下:
UnionFindSet(const T* sorce, size_t num)
{for (size_t i = 0; i < num; i++){_a.push_back(sorce[i]);_indexmap[sorce[i]] = i;}
}
最后将容器_ufs的长度扩容到num,并将每个元素的值都初始化为-1,那么完整的代码就如下:
UnionFindSet(const T* sorce, size_t num):_ufs(num,-1)
{for (size_t i = 0; i < num; i++){_a.push_back(sorce[i]);_indexmap[sorce[i]] = i;}
}
我们可以使用下面的代码来进行以下测试:
int main()
{string s1[] = { "张三","李四","王五","赵六" };UnionFindSet<string> uf(s1, 4);return 0;
}
通过调试我们便可以看到这个容器里面的内容如下:
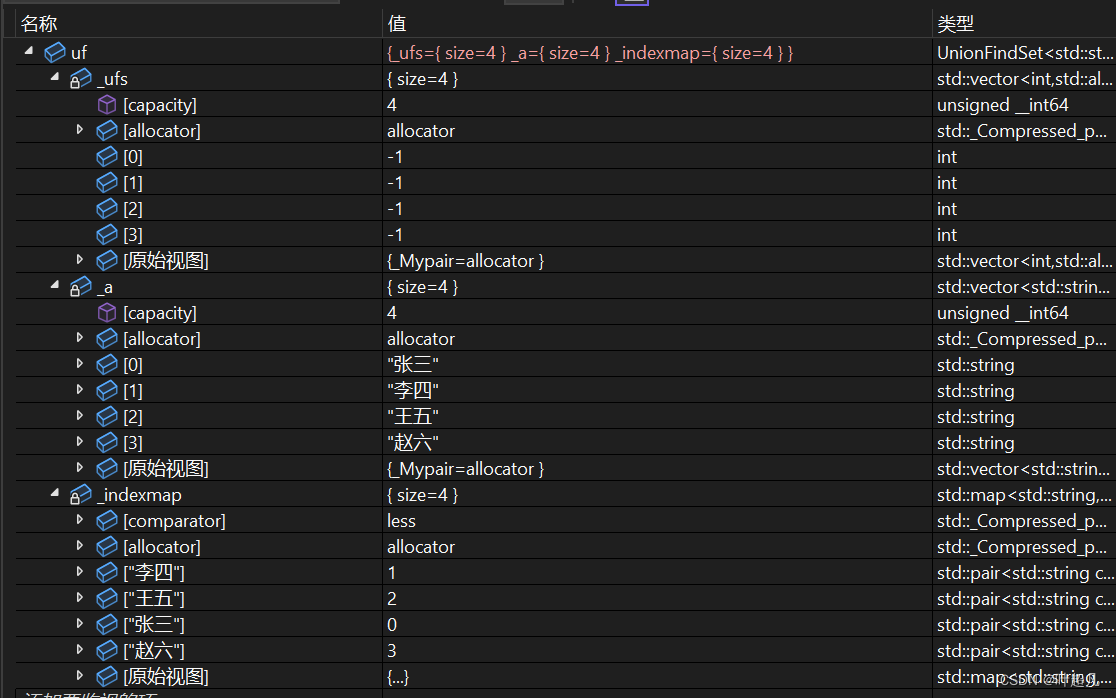
因为我们没有做出任何的合并操作所以ufs数组里面每个元素的值都是-1,_a数组里面记录的是下标所对应的元素,0对应的是张三,1对应的是李四,2对应的是王五,3对应的是赵六,然后_indexmap里面就记录的是元素对应的下标,经过仔细的对比可以看到里面记录的内容和数组中的内容相对应,那么我们的构造函数就实现完成了,接下来来看查找函数。
FindRoot
FindRoot函数就查找一个元素的根节点,如果一个节点不为根节点那么在数组里面它存储的就是它的父节点的下标,如果一个节点为根节点那么它存储的就是当前树种含有节点的个数的赋值,所以在函数里面我们可以创建一个while循环在循环里面一直提取数组中记录的下标,直到下标对应的值为负数位置,那么这里的代码就如下:
size_t FindRoot(T tmp)
{int x = _indexmap.find(tmp)->second;while (_ufs[x] >= 0){x = _ufs[x];}return x;
}
Union
传递两个元素给Union函数,那么该函数就能将两个元素所在的树进行合并,在函数的开始我们先判断一下这两个元素所在树的根节点是否相同,如果相同如果不相同的话我们就进行合并,那么这里的代码就如下:
void Union(T tmp1, T tmp2)
{size_t x1 = FindRoot(tmp1);size_t x2 = FindRoot(tmp2);if (x1 != x2){//根节点不相等才进行合并}
}
合并的过程很简单将某个根节点的值加到另外一个根节点上,然后将值更改成为另外一个根节点的下标即可,那么这里的代码就如下:
void Union(T tmp1, T tmp2)
{size_t x1 = FindRoot(tmp1);size_t x2 = FindRoot(tmp2);if (x1 != x2){//根节点不相等才进行合并_ufs[x1] += _ufs[x2];_ufs[x2] = x1;}
}
SetCount
这个函数的功能就是统计当前容器里面存在几棵树,那么这里我们直接通过循环遍历数组_ufs,里面存在几个元素为负数的节点就说明当前容器里面存在几棵树,那么这里的代码就如下:
size_t SetCount()
{size_t num = 0;for (auto ch : _ufs){if (ch < 0){num++;}}return num;
}
并查集实战
题目一:省份数量
题目详细:
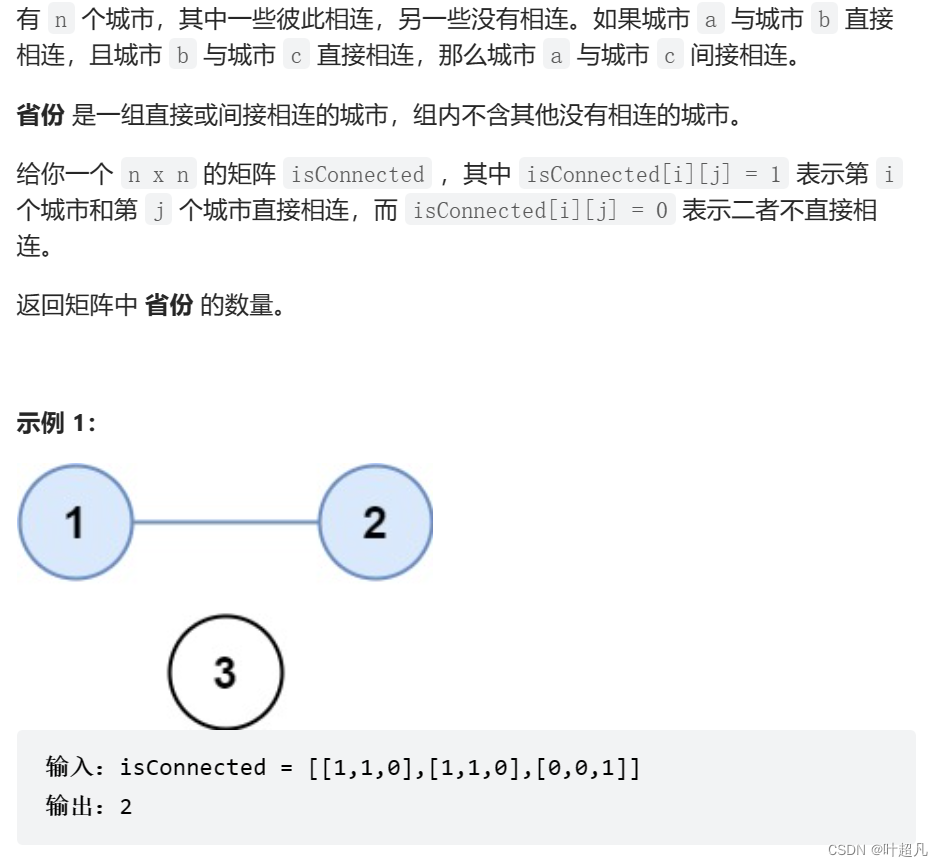
题目链接->点击此处尝试做题
题目解析
有了并查集之后做这种题简直就是小菜一碟,首先题目给了我们一个二维数组,这个数组里面表示各个城市之间的相连接情况,如果isConnected[0][1]等于1,那么这就表示1号城市和2号城市相联通,然后把一群相互联接的城市称为省份,最后题目要求我们根据一个二维数组来判断当前存在多少个省份,那么这里我们就可以先创建一个并查集对象,然后创建一个内嵌for循环判断二维数组中相互链接的城市,如果一个第i号城市和第j号城市相互连接的话就使用并查集对这两个城市进行合并,遍历完成之后就可以返回并查集中的SetCount函数来结束本题,因为题目传递的参数是一个vector<vector<int>>的容器,而我们上面实现的并查集的构造函数需要一个数组,所以为了方便我们对上面的类进行简化,让其专门服务于int类型的数据那么这里的代码如下:
class UnionFindSet
{
public:UnionFindSet(int size): _set(size, -1){}size_t FindRoot(int x){while(_set[x] >= 0)x = _set[x];return x;}void Union(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);if(root1 != root2){_set[root1] += _set[root2];_set[root2] = root1;}}size_t SetCount(){size_t count = 0;for(size_t i = 0; i < _set.size(); ++i){if(_set[i] < 0)count++;}return count;}private:std::vector<int> _set;
};
然后这道题的代码就如下:
int findCircleNum(vector<vector<int>>& isConnected) {UnionFindSet uf(isConnected.size());for(int i=0;i<isConnected.size();i++){for(int j=0;j<isConnected[0].size();j++){if(i!=j&&isConnected[i][j]==1){uf.Union(i, j);}}}return uf.SetCount();
}
测试的结果如下:
可以看到运行的结果是正确的。
题目二:等式方程的可满足性

题目链接->点击此处尝试做题
题目解析
这道题很明显也是使用并查集进行解决,数组中提供很多表达式,那么我们首先创建一个for循环将表达式中所用相等的元素都合并到一起,然后再创建一个循环判断每个不相等的表达式看两遍的元素是否属于同一个树,如果是树的话就直接返回false,如果不属于同一个树的话就接着往下进行判断,如果所有元素都判断完并且没有出错的话就返回true,题目给的参数形式如下:
bool equationsPossible(vector<string>& equations) {}
我们不知道元素个数,所以这里直接将空间拉到最大一共有26个因为字母,那么这里就开26个大小,然后使用相对映射法进行合并字符a对应的是0,字符b对应的是1这样一直往后,那么这里的代码就如下:
bool equationsPossible(vector<string>& equations) {UnionFindSet uf(26);for(auto ch:equations){if(ch[1]=='='){uf.Union(ch[0]-'a', ch[3]-'a');}}for(auto ch:equations){if(ch[1]=='!'){if(uf.FindRoot(ch[0]-'a')==uf.FindRoot(ch[3]-'a')){return false;}}}return true;}
代码的运行结果如下:
可以看到运行的结果是正常的。
相关文章:

数据结构---并查集
目录标题 为什么会有并查集并查集的原理模拟实现并查集准备工作构造函数FindRootUnionSetCount 并查集实战题目一:省份数量题目解析题目二:等式方程的可满足性题目解析 为什么会有并查集 这里可以使用生活中的一个例子来带着大家理解并查集,…...

iOS transform rotate总结
研究了一下transform的旋转设置,调了半天还以为是旋转写错了,发现是两个不同的view对象写错了,不管怎么说,还是记录一下旋转相关的操作吧。 参数都是弧度。 以一个图片来举例。 let img UIImageView.init() img.image UIImage…...

关于axios请求java接口中的@RequestParam、@PathVariable及@RequestBody不同接参类型的用法
一、前端传json对象,后端指定接收json对象中的哪个参数。 (1)前端请求 axios({//请求方式method:post,//后端接口路径url:http://127.0.0.1:8080/api/deleteUserById,//注意这里使用的是params,该属性负责把属性名和属性值添加到url后面,一般和get配合使…...
)
两个点云的重叠部分查找(附open3d python 代码)
方案1 使用 compute_point_cloud_distance: 它计算源点云中的每个点到目标点云中最近点的距离。距离近的点就是重叠点,距离远的点就是非重叠点 方案2 把两个点云变成2个集合set 数据类型,然后求集合的交集就行了,交集就是重叠点…...

PDF文件转换成word软件有哪些?分享两个文件格式转换软件
在日常办公中,我们经常使用各种办公软件,其中PDF和Word是最常见的两种格式。相较于Word文件,PDF文件具有更强的兼容性和安全性,因此我们通常会选择以PDF格式分享文件。然而,如果我们需要提取PDF文件中的部分内容&#…...

redis数据库
目录 1.关系型数据库与非关系型数据库 关系型数据库 非关系型数据库 区别 2.redis 3.安装redis 1.关系型数据库与非关系型数据库 关系型数据库 关系型数据库是一个结构化的数据库,创建在关系模型(二维表格模型)基础上,一般面向…...

SpringMVC-mybatis,SQL语句中误用了desc关键字,导致报错。
17-Jul-2023 21:26:22.295 淇℃伅 [RMI TCP Connection(2)-127.0.0.1] org.apache.catalina.core.ApplicationContext.log 1 Spring WebApplicationInitializers detected on classpath 17-Jul-2023 21:26:22.621 淇℃伅 [RMI TCP Connection(2)-127.0.0.1] org.apache.catalin…...

adb笔记
打开拨号盘 adb shell am start -a android.intent.action.DIAL -d tel:*该命令通过dumpsys window命令获取当前设备的窗口信息,并使用grep mCurrentFocus过滤出包含"mCurrentFocus"关键字的行,从而获取当前活动窗口或应用程序的名称和包名。…...

RocketMQ教程-(5)-功能特性-顺序消息
顺序消息为 Apache RocketMQ 中的高级特性消息,本文为您介绍顺序消息的应用场景、功能原理、使用限制、使用方法和使用建议。 应用场景 在有序事件处理、撮合交易、数据实时增量同步等场景下,异构系统间需要维持强一致的状态同步,上游的事…...
)
Oracle TNS侦听器远程中毒(CVE-2012-1675)
Oracle TNS侦听器远程中毒(CVE-2012-1675) [oracleorac bin]$ netca -silent -responsefile /home/oracle/netca.rspParsing command line arguments:Parameter "silent" trueParameter "responsefile" /home/oracle/netca.rsp Done parsing command li…...
Springboot+Netty
目录 一、netty入门 二、启动方式 三、netty服务启动类 四、handler链 五、具体业务 六、 线程或者非spring管理的bean中获取spring管理的bean 七、效果 一、netty入门 Netty-导学_哔哩哔哩_bilibili 入门视频量比较大,最主要是了解netty的架构 netty官网&am…...

window.location.href is not a function
在使用uniapp跳转到外部页面时,使用window.location.href报错 解决: 当出现"window.location.href is not a function"的错误时,这通常是因为在某些浏览器中,window.location.href被视为只读属性,而不是函…...

STM32+FPGA的导常振动信号采集存储系统
摘 要 : 针 对 工 厂 重 要 设 备 运 输 途 中 可 能 损 坏 的情 况 , 本 文 设计 了一 套 采 用 STM32F103+F࿳…...
Eclipse memory analyzer 分析GC dump日志定位代码问题
1、问题描述: 使用命令 jstat -gcutil [pid] 查看JVM GC日志,发现生产系统频繁FullGC,大概几分钟一次,而且系统响应速度变慢很多 再使用 free -g 查看服务器内存全部占用,猜测是内存溢出了 2、导出dump日志 jmap -du…...

DSA之图(3):图的遍历
文章目录 0 图的遍历1 图的遍历方法1.1 深度优先搜索DFS1.1.1 DFS的思想1.1.2 邻接矩阵DFS的实现1.1.3 邻接矩阵DFS的代码实现1.1.4 非连通图的DFS遍历1.1.5 DFS算法效率分析 1.2 广度优先搜索BFS1.2.1 BFS的思想(连通图)1.2.2 BFS的思想(非连…...
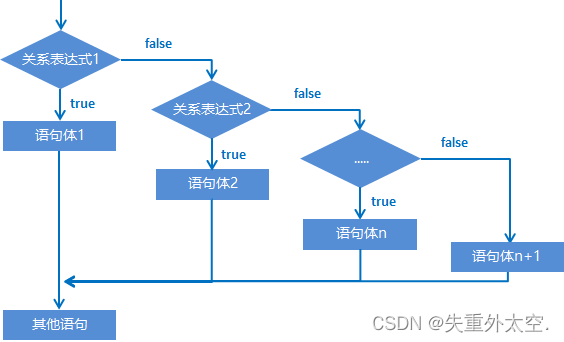
从零开始学习 Java:简单易懂的入门指南之for循环(四)
java基础知识 流程控制语句1.1 流程控制语句分类1.2 顺序结构 判断语句:if语句2.1 if语句格式1练习1:老丈人选女婿练习2:考试奖励第一种格式的细节: 2.2 if语句格式2练习1:吃饭练习2:影院选座 2.3 if语句格…...

Android 之 http/https原理和机制
http---HyperTextTransfer Protocol 超文本传输协议 超文本-文本、HTML http的工作方式 c/b结构 如浏览器访问到服务器。 即发送请求->相应。 Url-Http报文 http://www.baidu.com/path 协议类型:http or https or websocket 服务器地址 BaseUrl 路径&…...
mybatis源码研究、搭建mybatis源码运行的环境
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、有兴趣的可以关注一手。 前提 研究源码、对我们的技术提高还是很有帮助的。简单的源码建议从mybatis入手。涉及到的设计模式不是很多。需要下载mybatis的源码和父工程依赖。注意下载的mybatis中的父工程依…...

【算法基础:搜索与图论】3.5 求最小生成树算法(PrimKruskal)
文章目录 最小生成树介绍朴素Prim算法算法思路⭐例题:858. Prim算法求最小生成树 Kruskal算法算法思路⭐例题:859. Kruskal算法求最小生成树 最小生成树介绍 最小生成树 有关树的定义 生成子图:生成子图是从原图中选取部分节点以及这些节点…...
扩展Ceph集群实现高可用
...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
