选择适合产品需求管理的项目管理系统,打造完美项目流程!
一般来说,互联网产品经理收到的需求一般分为业务需求、用户需求和产品功能需求。业务需求主要包括战略和规则需求;用户需求一般是真实反馈、真实需求、吐槽、建议等。;功能需求主要围绕产品的旧功能问题进行升级,bug处理、技术问题、新功能实现需求等。当然,随着产品开发版本的迭代,对产品的需求会越来越大,最终形成一个完整的产品。要管理好这些需求,必须结合各开发阶段的实际情况。
在管理产品需求之前,我们应该优先考虑需求。不同阶段的产品需求也不同。一个产品成功上线,必须经历几个需求阶段:
第一阶段是初级产品(0-1产品)阶段。我们优先满足产品的基本需求或必要性,然后是先进的概念需求,最后是价值层面的需求。概念需求主要以战略需求和业务需求为出发点,所有需求都应围绕公司的战略发展目标确定,优先满足。
第二阶段是创意阶段。创意阶段的需求应根据公司现状、行业环境、市场环境和竞争产品环境综合考虑。本产品应具有创意模型。
第三阶段是研发阶段。几乎所有的产品经理和开发人员都参与到产品研发的每一个过程中来。这一阶段也是两者深度互动的阶段,需求管理也是最全面、最丰富、最严谨的。
第四阶段是内部测试阶段。本阶段的工作内容主要是发现和修改产品错误,首先是明确和验收现有需求是否正确。
第五阶段是产品发布后的需求。这个阶段主要是用户反馈。例如,收集用户对产品使用的真实反馈和建议,甚至取笑产品经理,做好信息收集和整理,研发人员应迅速给出合理的解决方案。
最后一个阶段是验收阶段。在这个阶段,产品的完整研发过程基本完成,整个项目几乎结束。在这个阶段,产品经理需要处理更多的事情,如验收测试、销售和市场推广。在验收的同时,我们需要做大量的文件沉淀,我们团队在 Zoho Projects项目管理系统上的文档沉淀和审查,后期和研发对接交付清单也非常清晰和简单。
在Zoho Projects项目管理系统的项目模块中,总结每一件事、重点、过程文档结构化沉淀、表格导出回顾更简单,项目成员对各环节沉淀确认文件一目了然,自然不会有争吵。
虽然每个阶段都有不同的需求,但我们的最终目标是尽快推出产品并顺利运行。只要围绕整体战略需求,分解为不同阶段的需求管理,这就是需求管理的完整过程。
需求管理的困难在于内容的描述和安排。产品人员和开发人员之间最有可能发生争议的是,开发的产品功能与原设计需求功能不一致。在大多数情况下,写需求的人是清楚的,看需求的人是清楚的,但产品不符合预期的要求。因为每个人对同一需求的理解都非常不同,我们需要面对面地同步需求,以确保理解一致,形成共识,而不是一劳永逸地发送文档进行云盘共享。
需求的变化来自很多因素,比如客户暂时无拘无束的想法,比如一开始没有形成共识文件,或者项目中的业务变化,以及负责人的变化。在开发过程中也可能会遇到无法控制的因素(这种情况很少)。每个因素都会导致需求的变化,这要求产品和开发人员在下一个版本迭代之前明确需求。
产品需求用什么项目管理系统做好?产品经理与开发和平共处并不难,各自做好本职工作,产品经理做好需求管理,多学习项目管理软件、待办工具(Zoho Projects等)。);开发人员认真了解需求,给出更多建议,耐心与产品经理深入互动。我相信开发人员不会因为产品人员不懂技术意孤行,产品人员也不会因为开发人员不懂客户就乱分配。如果他们想得到对方足够的信任,他们仍然需要长期的努力。
相关文章:
选择适合产品需求管理的项目管理系统,打造完美项目流程!
一般来说,互联网产品经理收到的需求一般分为业务需求、用户需求和产品功能需求。业务需求主要包括战略和规则需求;用户需求一般是真实反馈、真实需求、吐槽、建议等。;功能需求主要围绕产品的旧功能问题进行升级,bug处理、技术问题…...

@monaco-editor/react组件CDN加载失败解决办法
monaco-editor/react引入这个cdn资源会load失败 网上很多例子都是这样写的,我这样写monaco会报错 import * as monaco from monaco-editor; import { loader } from monaco-editor/react;loader.config({ monaco });改成这样 import * as monaco from monaco-edi…...

java对象的强引用,弱引用,软引用,虚引用
前言:java对象在java虚拟机中的生存状态,面试可能会有人问道,了解一下 这里大量引用 《疯狂Java讲义第4版》 书中的内容...
ubuntu ssh
前置 需要知道自己的ip 如果没有ifconfig sudo apt-get install net-tools然后 ifconfig中文用户 winr,输入 intl.cpl在git里,选zh_cn和UTF-8 安装 sudo apt-get install -y openssh-client openssh-server设置开机启动 sudo systemctl enable sshsudo nano…...

js:斐波那契额数列生成器Generator
请你编写一个生成器函数,并返回一个可以生成 斐波那契数列 的生成器对象。 斐波那契数列 的递推公式为 Xn Xn-1 Xn-2 。 这个数列的前几个数字是 0, 1, 1, 2, 3, 5, 8, 13 。 /*** return {Generator<number>}*/ var fibGenerator function*() {let pre…...
行列转换.
表abc: (建表语句在文章末尾) 想要得到: 方法一 with a as(select 年,产 from abc where 季1), b as(select 年,产 from abc where 季2), c as(select 年,产 from abc where 季3), d as(select 年,产 from abc where 季4) selec…...

CentOs 7利用iscaiadm工具发现并连接外接存储
CentOs 7利用iscaiadm工具发现并连接外接存储 1.1 使用iscsiadm发现存储 iscsiadm -m discovery -t st -p ${外接存储IP} # 执行结果may like ${外接存储IP}:3260,1 iqn.${存储唯一标识} 1.2 登入发现的存储 iscsiadm -m node -T iqn.${存储唯一标识} -p ${外接存储IP} -…...
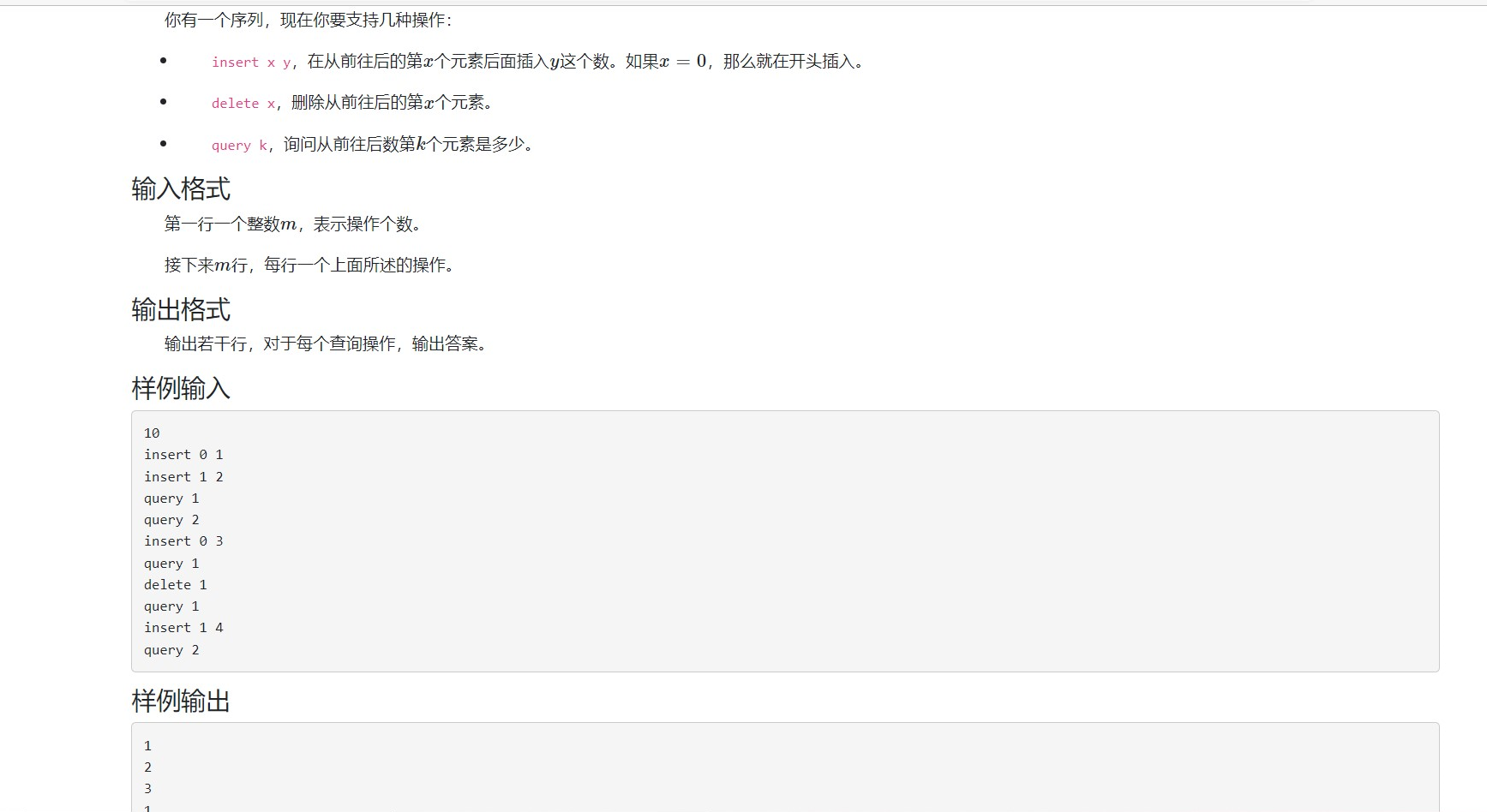
Java期末复习基础题编程题
文章目录 基础题记录实践题记录&&与C比较题目1:题目2:题目3: 基础题记录 编译型语言: 定义:在程序运行之前,通过编译器将源程序编译成机器码(可运行的二进制代码),以后执行这个程序时&…...
资深测试总结,自动化测试-ddt数据驱动yaml文件实战(详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 ddt 驱动 yaml/ym…...
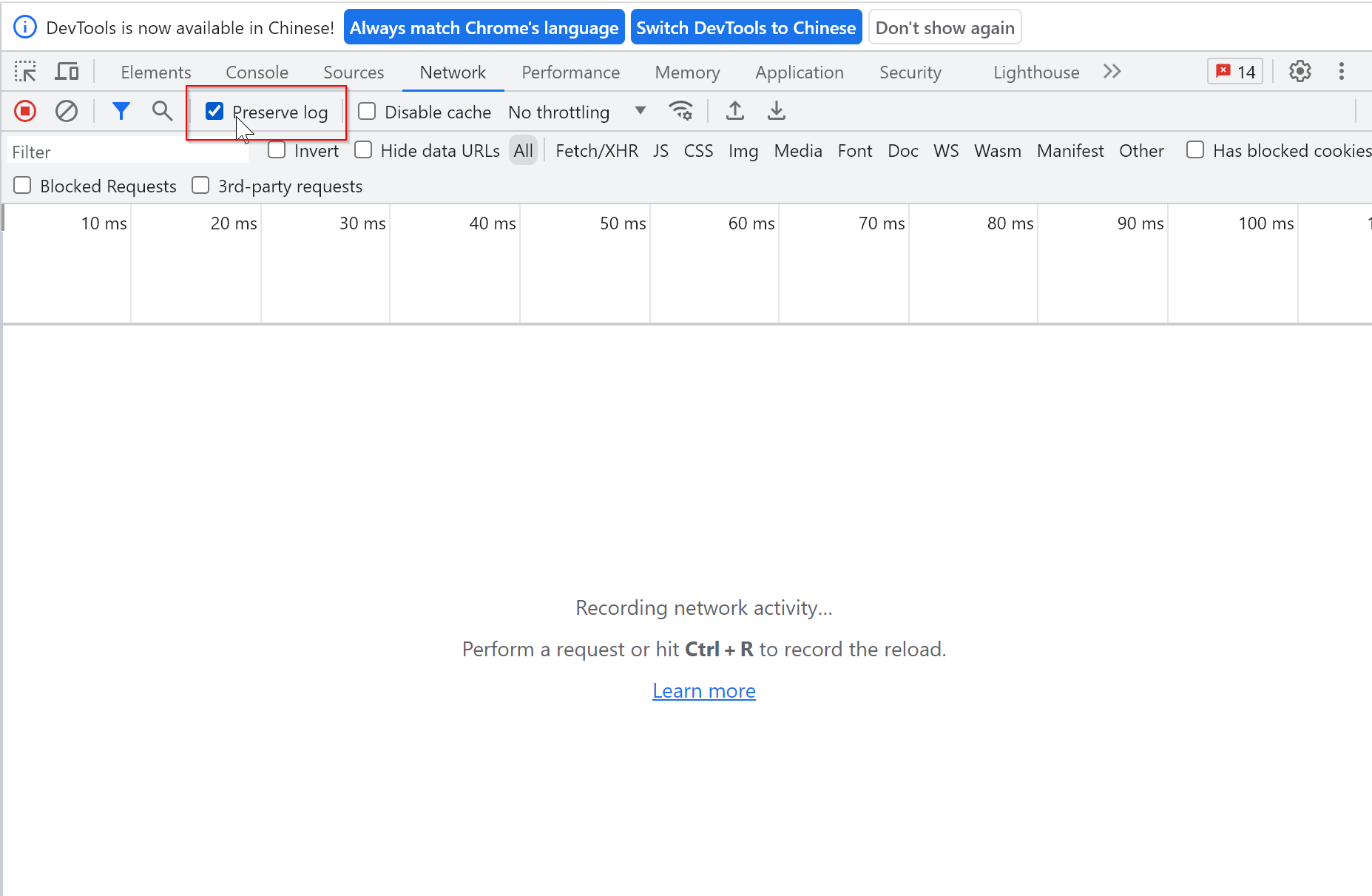
F12 浏览器调试模式页面刷新 network 日志刷新消失的解决办法
每次请求刷新后都把之前的请求记录刷新掉了,把preserve log勾选上后,所有的请求都会保留,再也不怕抓不到记录了。...
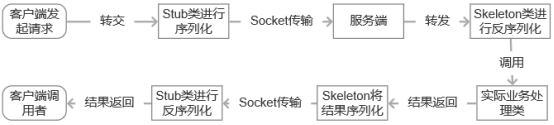
代理模式-对象的间接访问
现在朋友圈有好多做香港代购的微商,大部分网民无法自己去香港购买想要的商品,于是委托这些微商,告诉他们想要的商品,让他们帮我们购买。我们只需要付钱给他们,他们就会去香港购买,然后把商品寄给我们。这就…...

汽车产业链面临重大变革 大运乘用车加强产业布局 助力低碳出行
当前,国家“双碳”战略的全面实施,全球绿色产业发展理念的不断加深以及汽车产品形态、交通出行模式、能源消费结构变革所呈现的发展机遇等诸多因素,持续推动新能源汽车产业全面转型提速。据悉,2022年,中国新能源汽车销…...
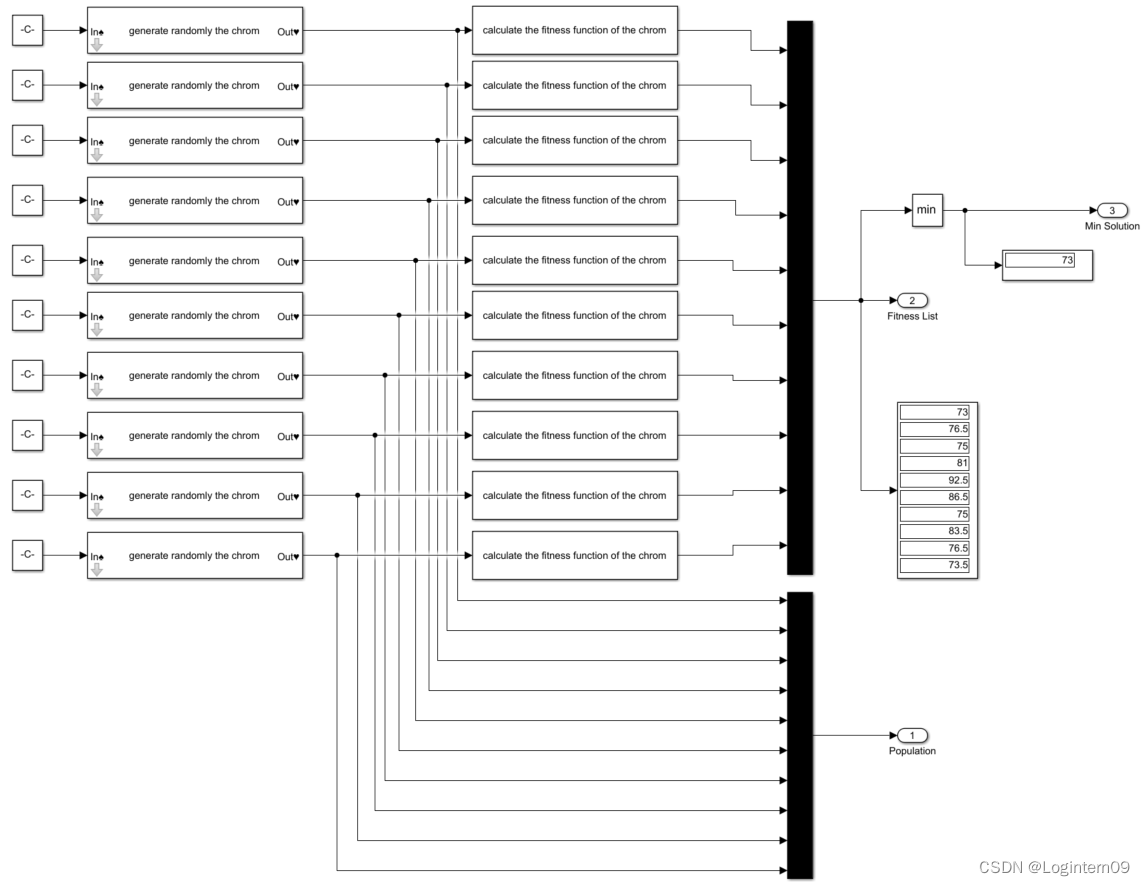
simulink与遗传算法结合求解TSP问题
前言:刚开始入门学习simulink,了解了基本的模块功能后想尝试从自己熟悉的领域入手,自己出题使用simulink搭建模型。选择的是TSP问题的遗传算法,考虑如何用simulink建模思想来实现一个简单TSP问题的遗传算法。 TSP问题描述 一个配…...

环境搭建-Ubuntu18.04.6系统TensorFlow BenchMark的GPU测试
1. 下载Ubuntu18.04.6镜像 登录阿里云官方镜像站:阿里巴巴开源镜像站-OPSX镜像站-阿里云开发者社区 2. 测试环境 Server OS:Ubuntu 20.04.6 LTS Kernel: Linux 5.4.0-155-generic x86-64 Docker Version:24.0.5, build ced0996 docker-com…...

C# 汇总区间
228 汇总区间 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区间范围…...
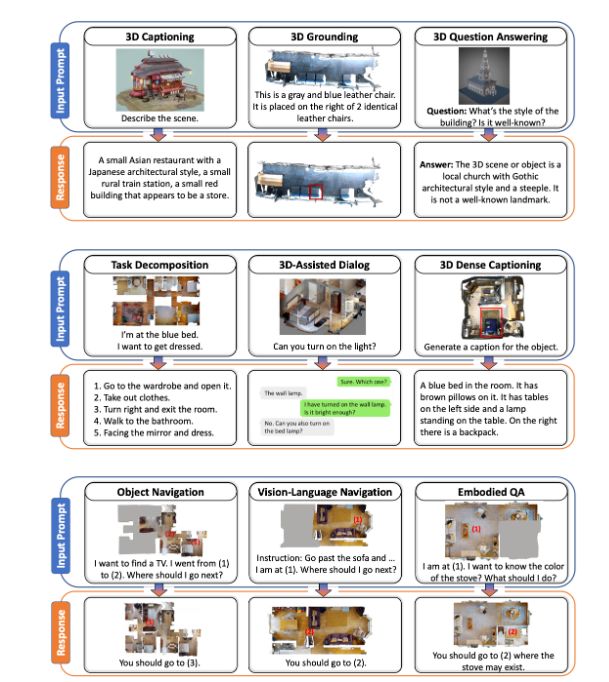
加利福尼亚大学|3D-LLM:将3D世界于大规模语言模型结合
来自加利福尼亚大学的3D-LLM项目团队提到:大型语言模型 (LLM) 和视觉语言模型 (VLM) 已被证明在多项任务上表现出色,例如常识推理。尽管这些模型非常强大,但它们并不以 3D 物理世界为基础,而 3D 物理世界涉及更丰富的概念…...
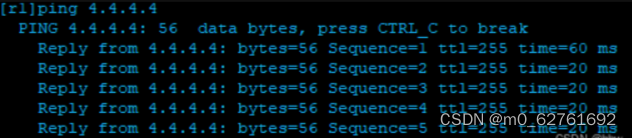
HCIA实验四
一.实验要求: 1、R4为ISP,其上只能配置IP地址;R4与其他所有直连设备间均使用共有IP; 2、R3 - R5/6/7为MGRE环境,R3为中心站点; 3、整个网络配置OSPF环境,IP基于172.16.0.0/16网段划分&#x…...

常见的算法
查找算法 基本查找 Demo1 public static boolean basicSearch(int index,int[] arr){for (int i 0; i < arr.length; i) {if (indexarr[i]){return true;}}return false; } Demo2 //顺序查找,考虑重复,返回查找内容的索引 public static ArrayLis…...
Jetbrains 2023.2教程
IDEA 2023.2 激活演示 Pycharm 2023.2 激活演示 WebStorm 2023.2 激活演示 Clion 2023.2 激活演示 DataGrip 2023.2 PhpStorm 2023.1.4 激活演示(2023.2尚未发布) RubyMine 2023.2 激活演示 获取方式 仔细看每一个工具演示的图片 本文由 mdnice …...

OpenLayers入门,OpenLayers地图初始化时如何设置默认缩放级别、设置默认地图中心点、最大缩放级别和最小缩放级别以及默认坐标系
专栏目录: OpenLayers入门教程汇总目录 前言 OpenLayers地图初始化时如何设置默认缩放级别、初始化时设置默认地图中心点、设置最大缩放级别和最小缩放级别,超过缩放级别用户无法再放大和缩小,和设置默认坐标系。 二、依赖和使用 "ol": "^6.15.1"使用…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
