杭州多校2023“钉耙编程”中国大学生算法设计超级联赛(4)
| 1003 | Simple Set Problem |
首先将元素的值 x 以及所属集合的编号 y 作为二元组 (x,y) 存入数组,然后按照 x 升序排列,
之后使用双指针扫描数组(尺取法),当区间内出现了所有编号时更新答案的最小值,
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <tuple>
#include<functional>
using namespace std;
const int N = 2e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
int n,k,m;
int a[N];
void solve()
{cin>>n;vector<PII> a;for(int i=1;i<=n;i++){int cnt;cin>>cnt;for(int j=1;j<=cnt;j++){int x;cin>>x;a.push_back({x,i});}}sort(a.begin(),a.end());int res=2e18;int l=0,r=0;vector<int> cnt(n+10,0);int now=0;m=a.size();while(r<m){if(cnt[a[r].second]==0) now++;cnt[a[r].second]++;while(now>=n){if(cnt[a[l].second]-1==0){break;} cnt[a[l].second]--;l++;}if(now==n){res=min(res,a[r].first-a[l].first);}r++;}cout<<res<<"\n";
}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();}| 1009 | WO MEI K |
k=2,相当于所有两个不同的点之间只出现过一条边的个数的和,可以考虑每条边的贡献,答案就是所有边的贡献的和,
大于2的时候只是乘上C(N-2,K-2)而已,因为求得是期望最后除上总数C(N,K)即可
所以问题就变成当k=2的时候如何求每个边的贡献和
首先因为是树,n点n-1边,我们可以把u-v的边,当成是v点的权值,把边权变成点权,
然后问题就可以转换成计算每个点不重复的情况下的贡献总和
我们可以使用树上启发式合并 DSG(英文好像是这样的忘了....)
我们每次把信息合并到父亲节点,且顺便计算子树节点中的贡献
我们需要一个cnt数组记录当前子树而言有多少个点是必定经过C边权的个数
sum数组记录当前子树而言没经过当前节点的边权
V容器是记录当前子树下每个不同权值c的最近儿子节点
每个合并信息的时候顺便计算出当前子树下面有多少个点的权值和其根节点权值一样,先把子树内的贡献先计算了,其贡献就是sum[v]*(siz[u]-cnt[col[u]]
然后把和根节点权值相同的信息给更新即可
树上启发式合并简单说就是优先遍历轻儿子,最后遍历重儿子,重儿子信息不清空,轻儿子信息清空
dfs0函数就是-1就是清空轻儿子信息,1是合并轻儿子信息
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <tuple>
#include<functional>
using namespace std;
const int N = 2e5+10,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
int n,k,m;
int a[N];
int fact[N],infact[N];
int son[N],siz[N],col[N],sum[N];
int tot,ans;
bool vis[N];
int cnt[N];
vector<PII> g[N];
vector<int> V[N];
int qmi(int a, int k, int p) // 求a^k mod p
{int res = 1 % p;while (k){if (k & 1) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1;}return res;
}
void init(){fact[0]=infact[0]=1;for(int i=1;i<N;i++){fact[i]=(LL)fact[i-1]*i%mod;infact[i]=(LL)infact[i-1]*qmi(i,mod-2,mod)%mod;}
}
int C(int n,int m){if(m<0||n<0||n<m) return 0;return (LL)fact[n] * infact[m] % mod * infact[n - m] % mod;
}
void dfs1(int u,int fa){siz[u]=1;son[u]=0;for(auto [v,w]:g[u]){if(v==fa) continue;dfs1(v,u);siz[u]+=siz[v];col[v]=w;if(siz[v]>siz[son[u]]) son[u]=v;}
}
void dfs0(int u,int fa,int ty){if(ty==-1){V[col[u]].clear();cnt[col[u]]-=sum[u];}else{//col[u]就是fa到u边的权值,把每个边的权值记录下来点if(!vis[u]) V[col[u]].push_back(u);cnt[col[u]]+=sum[u];}for(auto [v,w]:g[u]){if(v==fa) continue;dfs0(v,u,ty);}
}
void dfs2(int u,int fa){for(auto[v,w]:g[u]){if(v==fa||v==son[u]) continue;dfs2(v,u);dfs0(v,u,-1);}if(son[u]) dfs2(son[u],u);for(auto [v,w]:g[u]){if(v==fa||v==son[u]) continue;dfs0(v,u,1);}if(u==1) return ;sum[u]=siz[u]-cnt[col[u]];//sum[u]就是u子树的大小减去子树有多少条边是一样的权值for(auto v:V[col[u]]){vis[v]=true;tot=(tot+sum[v]*(siz[u]-cnt[col[u]]%mod))%mod;}V[col[u]].clear();V[col[u]].push_back(u);cnt[col[u]]=siz[u];
}
void solve()
{cin>>n;ans=tot=0;for(int i=1;i<=n;i++){cnt[i]=0;vis[i]=false;g[i].clear();}for(int i=1;i<n;i++){int x,y,w;cin>>x>>y>>w;g[x].emplace_back(y,w);g[y].emplace_back(x,w);}dfs1(1,0);dfs2(1,0);for(int i=1;i<=n;i++){for(auto v:V[i]){tot=(tot+sum[v]*(n-cnt[i])%mod)%mod;}//n-cnt[i] 就是除了这个子树外的点V[i].clear();}int d=qmi(n-1,mod-2,mod)*qmi(n,mod-2,mod)%mod;for(int i=2;i<=n;i++){int res=d*(i-1)%mod*i%mod*tot%mod;ans^=res;}cout<<ans<<"\n";
}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;init();cin>>t;while(t--) solve();}| 1011 | Circuit |
额题目就是个例题,有向图的最小环用弗洛伊德求解即可
把问题分解为一个dp问题,子集就是最大编号使用1,2,3,...,k的点
这些情况的总和相加
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <tuple>
#include<functional>
using namespace std;
const int N = 510,mod=998244353;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;
int n,k,m;
int sum[N][N];
int dis[N][N];
vector<PII> g1[N],g2[N];void solve()
{cin>>n>>m;int len=2e18;int ans=0;for(int i=1;i<=n;++i)for(int j=1;j<=n;++j){dis[i][j]=1e18;if(i==j) dis[i][j]=0;sum[i][j]=1;}for(int i=1;i<=n;++i) g1[i].clear(),g2[i].clear();for(int i=1;i<=m;++i){int x,y,w;cin>>x>>y>>w;dis[x][y]=w; sum[x][y]=1;g1[x].push_back({y,w});g2[y].push_back({x,w});}for(int k=1;k<=n;++k){for(int i=1;i<=n;++i)for(int j=1;j<=n;++j){if(i==k||j==k) continue;if(dis[i][j]<dis[i][k]+dis[k][j]) continue;if(dis[i][j]>dis[i][k]+dis[k][j]) sum[i][j]=0;dis[i][j]=dis[i][k]+dis[k][j];sum[i][j]=(sum[i][j]+sum[i][k]*sum[k][j]%mod)%mod;}for(auto x:g1[k])for(auto y:g2[k]){if(x.first>k) continue;if(y.first>k) continue;int C=dis[x.first][y.first]+x.second+y.second;int S=sum[x.first][y.first];if(C>len) continue;if(len>C) ans=0;len=C; ans=(ans+S)%mod;}}if(len>=1e15) cout<<"-1 -1\n";else cout<<len<<" "<<ans<<"\n";
}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();}| 1012 | a-b Problem |
首先贪心的想拿走一个石头,等于自己得到ai分,对面失去bi分
所以直接按照ai+bi大小拿即可,每次第一个人能这个总和最大,第二个人拿这个总和最小,我用平衡树来动态查找删除了
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <tuple>
#include<functional>
using namespace std;
const int N = 2e5+10,mod=1e9+7;
#define int long long
typedef long long LL;
typedef pair<int, int> PII;int n,m,k;
vector<PII>g[N];
PII a[N];
void solve()
{set<PII> st1,st2;cin>>n;for(int i=1;i<=n;i++){cin>>a[i].first>>a[i].second;st1.insert({a[i].first+a[i].second,i});st2.insert({-a[i].second-a[i].first,i});}int res=0;for(int i=1,now=0;i<=n;i++,now^=1){int id=0;if(now==0){auto it=st1.rbegin();id=(*it).second;res+=a[id].first;}else{auto it=st2.begin();id=(*it).second;res-=a[id].second;}st1.erase(st1.lower_bound({a[id].first+a[id].second,id}));st2.erase(st2.lower_bound({-a[id].second-a[id].first,id}));}cout<<res<<"\n";
}
signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t=1;cin>>t;while(t--) solve();}相关文章:
)
杭州多校2023“钉耙编程”中国大学生算法设计超级联赛(4)
1003Simple Set Problem 首先将元素的值 x 以及所属集合的编号 y 作为二元组 (x,y) 存入数组,然后按照 x 升序排列, 之后使用双指针扫描数组(尺取法),当区间内出现了所有编号时更新答案的最小值, #includ…...
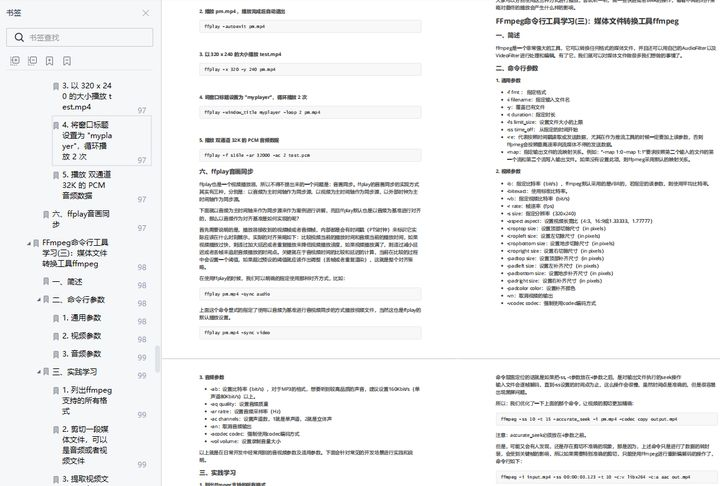
音视频入门之音频采集、编码、播放
作者:花海blog 今天我们学习音频的采集、编码、生成文件、转码等操作,我们生成三种格式的文件格式,pcm、wav、aac 三种格式,并且我们用 AudioStack 来播放音频,最后我们播放这个音频。 使用 AudioRecord 实现录音生成…...

在 Linux 系统中,如何发起POST/GET请求
在 Linux 系统中,可以使用命令行工具 curl 或者 wget 来发送 POST 请求。这两个工具都是非常常用的命令行工具,可以通过命令行直接发送 HTTP 请求。 1. 使用 curl 发送 POST 请求: curl -X POST -H "Content-Type: application/json&q…...
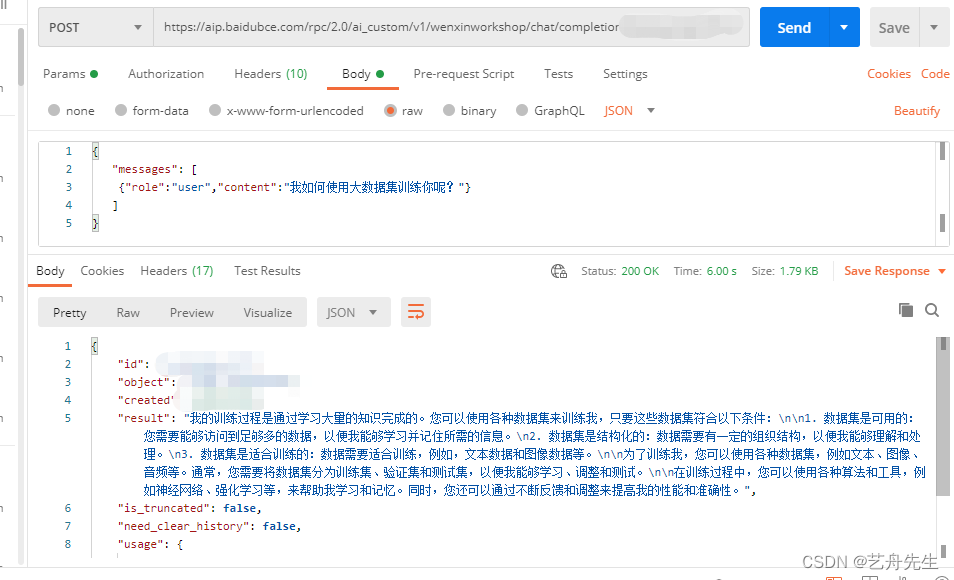
文心一言大数据模型-文心千帆大模型平台
官网: 文心千帆大模型平台 (baidu.com) 文心千帆大模型 (baidu.com) 模型优势 1、模型效果优:所需标注数据少,在各场景上的效果处于业界领先水平 2、生成能力强:拥有丰富的AI内容生成(AIGC)能力 3、应用…...
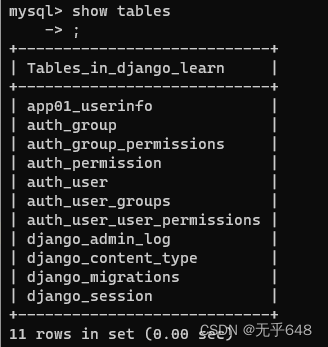
django学习笔记(1)
django创建项目 先创建一个文件夹用来放django的项目,我这里是My_Django_it 之后打开到该文件下,并用下面的指令来创建myDjango1项目 D:\>cd My_Django_itD:\My_Django_it>"D:\zzu_it\Django_learn\Scripts\django-admin.exe" startpr…...

postgresql主从搭建
postgresql主从搭建 主从服务器分别安装好postgresql 主库 创建数据库热备帐号replica,密码123456为例,则执行以下命令 create role replica login replication encrypted password 123456;打开 pg_hba.conf 配置文件,设置 replica 用户白…...

将Parasoft和ChatGPT相结合会如何?
ChatGPT是2023年最热门的话题之一,是OpenAI训练的语言模型。它能够理解和生成自然语言文本,并接受过大量数据的训练,包括用各种编程语言编写的许多开源项目的源代码。 软件开发人员可以利用大量的知识库来协助他们的工作,因为它具…...

Go text/template详解:使用指南与最佳实践
I. 简介 A. 什么是 Go text/template Go text/template 是 Go 语言标准库中的一个模板引擎,用于生成文本输出。它使用类似于 HTML 的模板语言,可以将数据和模板结合起来,生成最终的文本输出。 B. Go text/template 的优点 Go text/templa…...

Stable Diffusion在各种显卡上的加速方式测试,最高可以提速211.2%
Stable Diffusion是一种基于扩散模型的图像生成技术,能够从文本生成高质量的图像,适用于CG,插图和高分辨率壁纸等领域。 但是它计算过程复杂,使得它的生成速度较慢。所以研究人员就创造了各种提高其速度的方式,比如Xf…...

Java读取外链图片忽略ssl验证转为base64
最近在对接外部接口时遇到返回的图片所在的服务器全都没有ssl证书,导致在前端直接用img标签展示时图片开裂。于是转为通过后端获取,绕过ssl验证之后转为base64返回。记录一下代码段。 package com.sy.ai.common.utils;import cn.hutool.core.codec.Base…...
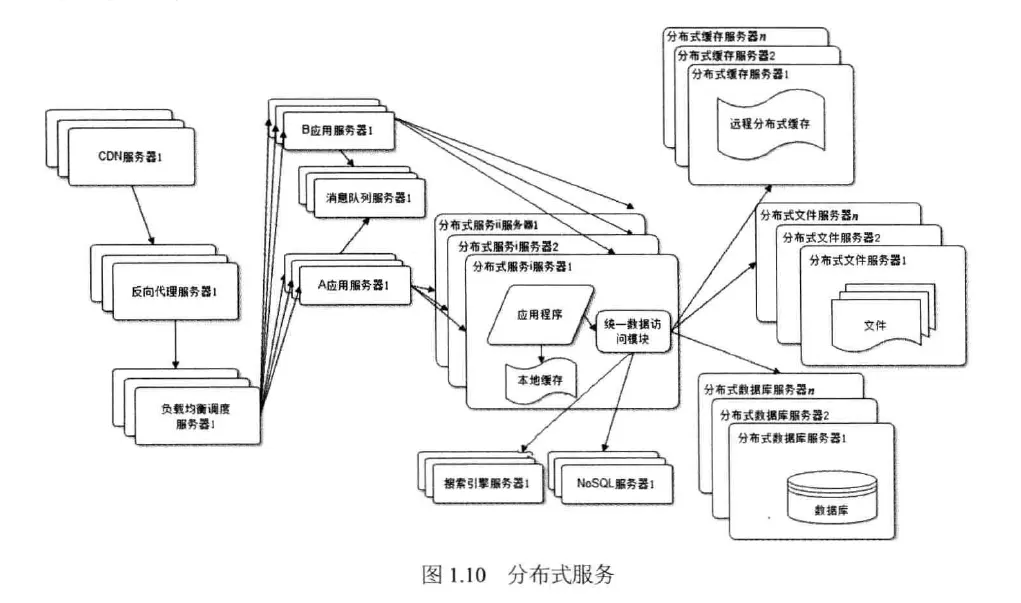
系统架构设计师 10:软件架构的演化和维护
一、软件架构演化 如果软件架构的定义是 SA{components, connectors, constraints},也就是说,软件架构包括组件、连接件和约束三大要素,这类软件架构演化主要关注的就是组件、连接件和约束的添加、修改与删除等。 二、面向对象软件架构演化…...
Windows 11 绕过 TPM 方法总结,通用免 TPM 镜像下载 (2023 年 7 月更新)
Windows 11 绕过 TPM 方法总结,通用免 TPM 镜像下载 (2023 年 7 月更新) 在虚拟机、Mac 电脑和 TPM 不符合要求的旧电脑上安装 Windows 11 的通用方法总结 请访问原文链接:https://sysin.org/blog/windows-11-no-tpm/,查看最新版。原创作品…...
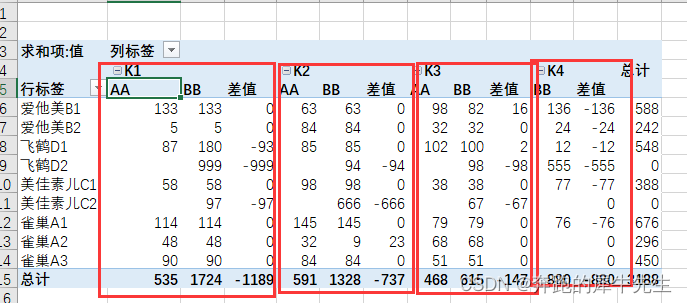
EXCEL,如何比较2个表里的数据差异(使用数据透视表)
目录 1 问题: 需要比较如下2个表的内容差异 1.1 原始数据喝问题 1.2 提前总结 2 使用EXCEL公式方法 2.1 新增辅助列: 辅助index 2.2 具体公式 配合条件格式 使用 3 数据透视表方法 3.1 新增辅助列: 辅助index 3.2 需要先打开 数据透视表向导 …...
字节抖音小程序,使用 uniapp 调起内置支付
字节抖音小程序,使用 uniapp 调起内置支付 第一步:提交订单 后端通过抖音预下单接口,提交支付订单信息。 预下单接口_小程序_抖音开放平台预下单接口 提交支付订单信息。 ## 使用限制 无 ## 接口说明 预下单接口需要保证同一app_id下每笔订…...

django模板继承和组件了解
1、模板继承 什么时候需要用到模板呢,比如我们在开发的页面的导航栏,你点不同的功能页面这个导航栏都是一样的,如果每个页面都要加上这个导航条会写重复代码,而且如果导航条有变化,每个页面都要修改,这个是…...

首屏优化,给以图片为背景的元素增加相似背景,优化用户体验,background-image 绘制规则
每日鸡汤:每个你想要学习的瞬间都是未来的你向自己求救 假设你的项目首页有个大大的图片作为背景,那么这个图片肯定会在网络不好的时候加载出来很慢,导致用户回看到一大片白屏,这样很影响体验。这也是老生常谈的首屏优化的问题。例…...
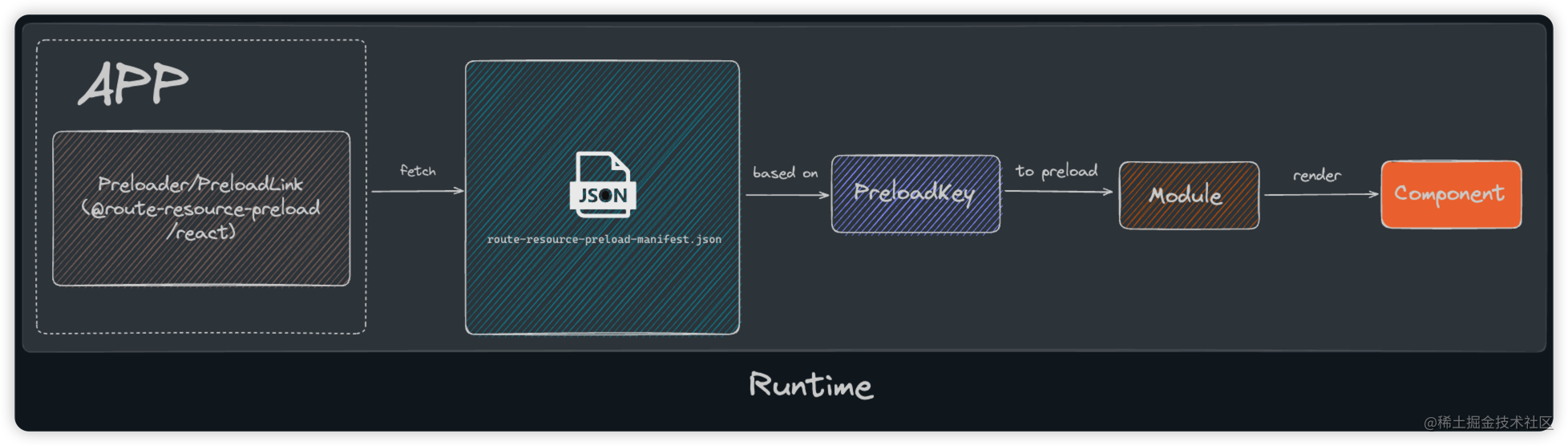
【用户体验分析报告】 按需加载组件,导致组件渲染卡顿,影响交互体验?组件拆包预加载方案来了!
首先,我们看一些针对《如何提升应用首屏加载体验》的文章,提到的必不可少的措施,便是减少首屏幕加载资源的大小,而减少资源大小必然会想到按需加载措施。本文提到的便是一个基于webpack 插件与 react 组件实现的一套研发高度自定义…...
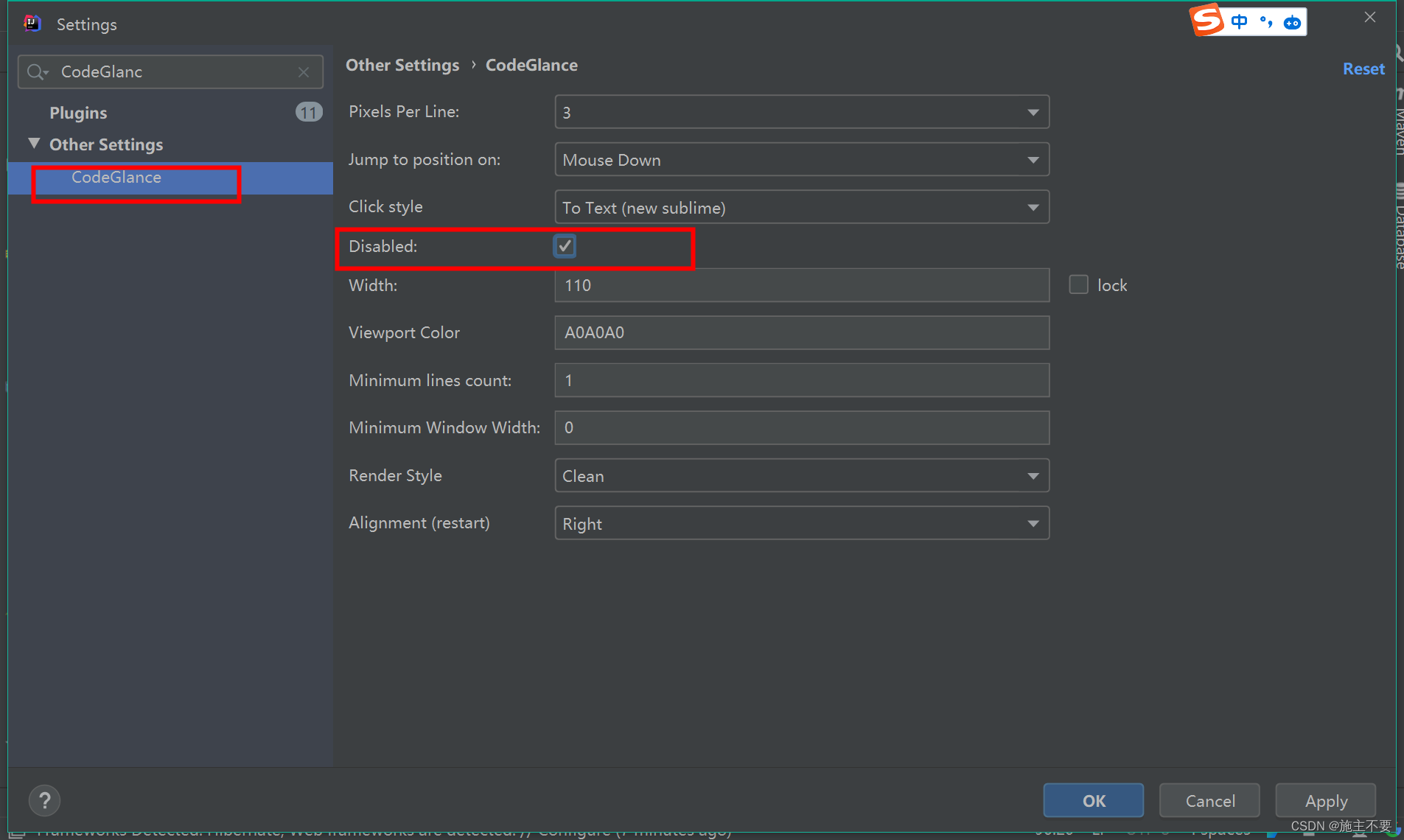
idea 关闭页面右侧预览框/预览条
idea 关闭页面右侧预览框 如图,预览框存在想去除 找了好多方法,什么去掉“setting->appearance里的show editor preview tooltips”的对钩;又或者在该预览区的滚动条上右键,“取消勾选show code lens on scrollbar hover”。都…...
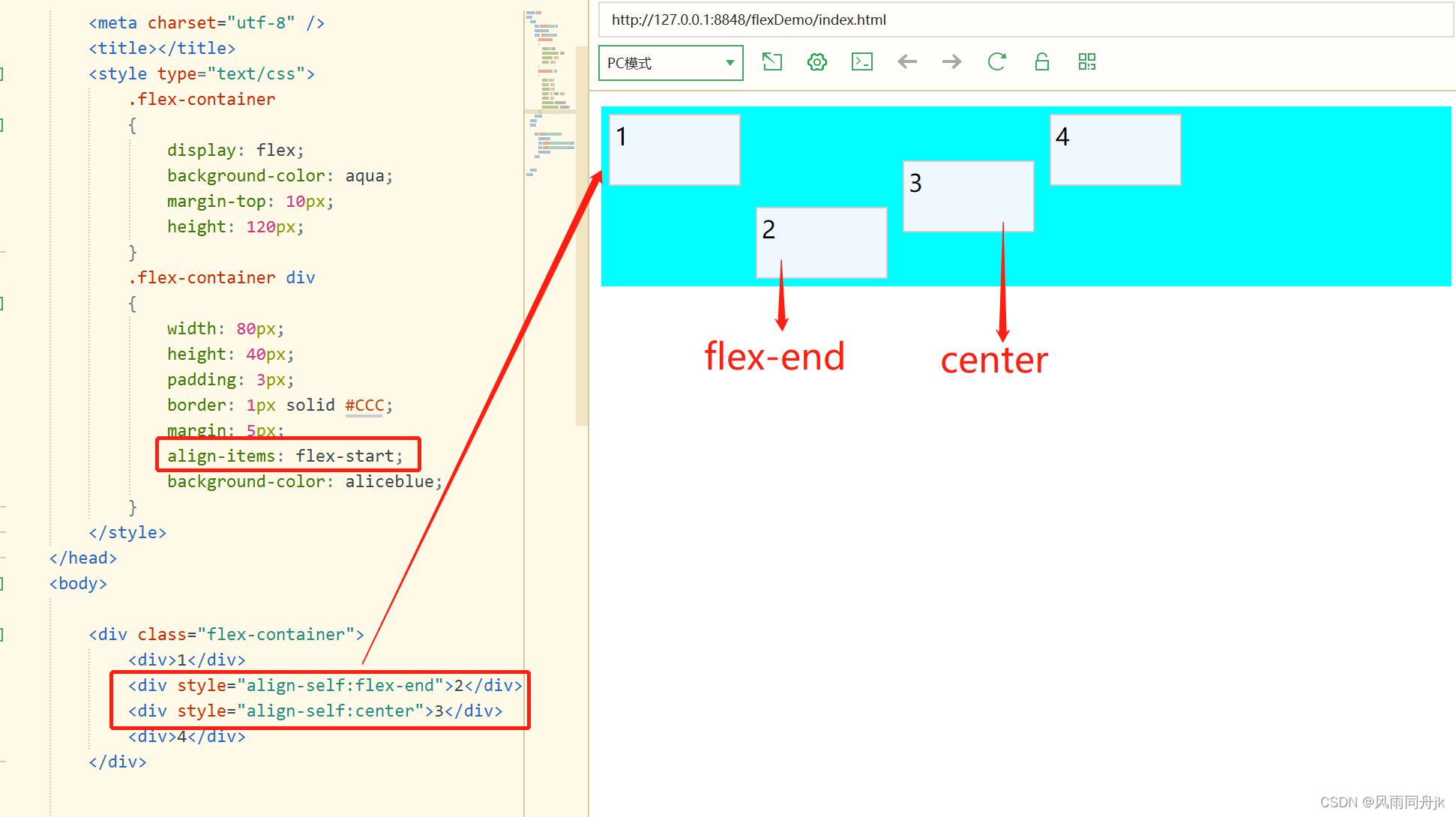
CSS3 Flexbox
Flex 是 Flexible Box 的缩写,意为弹性盒子布局。 CSS3中一种新的布局模式:W3C在2009年提出的一种布局方案,一种当页面需要适应不同的屏幕大小以及设备类型时确保元素拥有恰当的行为的布局方式。其目的是提供一种更加有效的方式来对一个容器…...
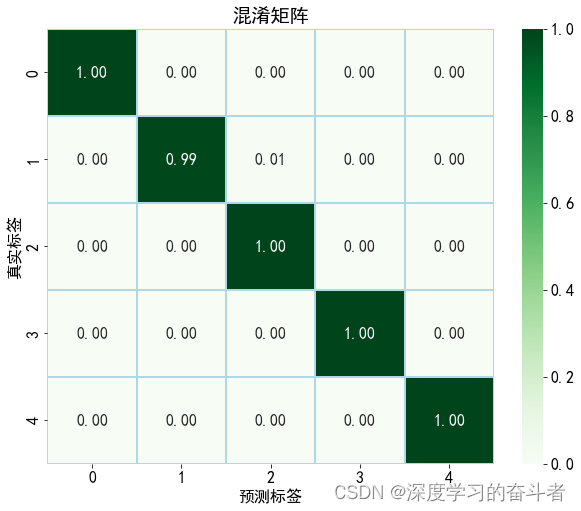
东南大学轴承故障诊断(Python代码,CNN模型,适合复合故障诊断研究)
运行代码要求: 代码运行环境要求:Keras版本>2.4.0,python版本>3.6.0 本次实验主要是在两种不同工况数据下,进行带有复合故障的诊断实验,没有复合故障的诊断实验。 实验结果证明,针对具有复合故障的…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

day51 python CBAM注意力
目录 一、CBAM 模块简介 二、CBAM 模块的实现 (一)通道注意力模块 (二)空间注意力模块 (三)CBAM 模块的组合 三、CBAM 模块的特性 四、CBAM 模块在 CNN 中的应用 一、CBAM 模块简介 在之前的探索中…...
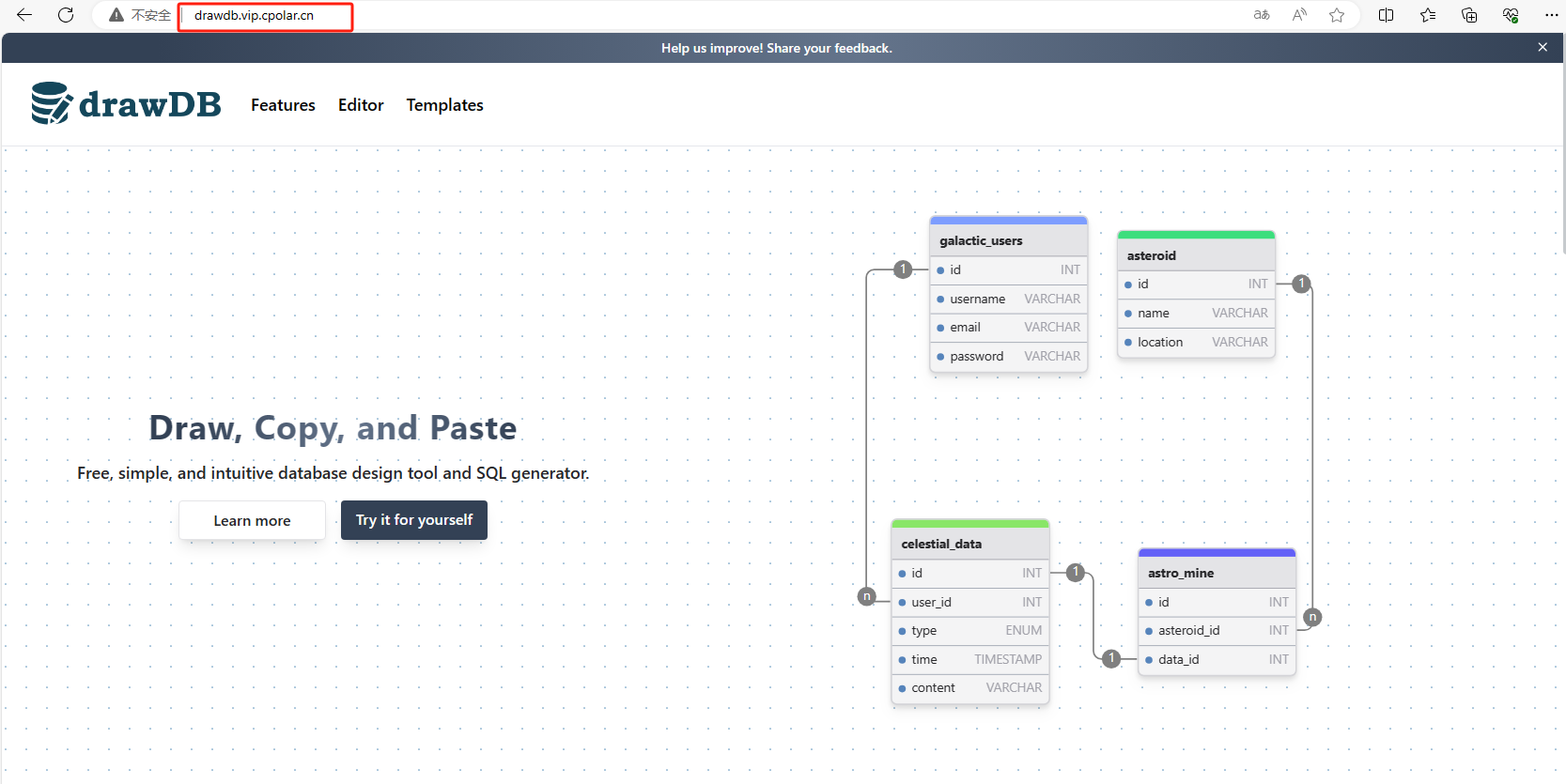
本地部署drawDB结合内网穿透技术实现数据库远程管控方案
文章目录 前言1. Windows本地部署DrawDB2. 安装Cpolar内网穿透3. 实现公网访问DrawDB4. 固定DrawDB公网地址 前言 在数字化浪潮席卷全球的背景下,数据治理能力正日益成为构建现代企业核心竞争力的关键因素。无论是全球500强企业的数据中枢系统,还是初创…...
