【视觉SLAM入门】4.3. (非线性最小二乘问题)优化算法实现-ceres和g2o, 图优化理论
"天道不争而善胜"
- 1. Ceres库
- 1.1 名词解释
- 1.2 具体例子
- 1.3 C++实现
- 1. 定义代价函数
- 2. 构建最小二乘问题
- 3. 配置求解器,开始优化
- 4. 优化完毕,查看结果
- 2. G2O(General Graphic Optimization)
- 2.1 图优化
- 2.2 具体例子
- 2.3 C++实现
- 1. 定义顶点
- 2. 定义边
- 3. 配置求解器
- 4. 配置图模型
- 5. 向图添加边
- 6. 执行优化
- 7. 查看
- 3. 总结
注意:有个概念需要通俗的了解一下
-
非线性最小二乘:它属于一种优化问题。即用一个模型来描述现实中的一系列数据时,模型的预测结果与实际的测量结果总会存在一定偏差,这一偏差就称为残差。非线性最小二乘的目的就是,调整模型的参数,使得总的残差最小。
-
优化算法:为获得更好的结果,而采取的方法
1. Ceres库
1.1 名词解释
Ceres求解最小二乘的问题通用形式如下:
min x 1 2 ∑ i ρ i ( ∣ ∣ f i ( x i 1 , . . . , x i n ∣ ∣ 2 ) s . t . l j ≤ x j ≤ u j \min\limits_x \;\frac{1}{2}\sum\limits_i\rho_i\Big(||f_i(x_{i_1},...,x_{i_n}||^2\Big) \\ s.t. \quad l_j \le x_j \le u_j xmin21i∑ρi(∣∣fi(xi1,...,xin∣∣2)s.t.lj≤xj≤uj
- 核函数: ρ ( ⋅ ) \rho(\cdot) ρ(⋅),用于在计算残差时对其进行加权,以减小噪声的影响。暂时取恒等函数
- 优化变量: min \min min 底下的,即 x 1 , . . . , x n x_1,...,x_n x1,...,xn
- 目标函数: 总的大式子,核函数取恒等函数的时候,它是许多项的平方和;
- 代价函数: f i f_i fi, SLAM中的误差项
- 边界: l j l_j lj 和 u j u_j uj 是优化变量的取值范围,分别是下界和上界,暂时取正负无穷
当核函数恒等时,整个问题就是无约束的最小二乘问题。
1.2 具体例子
设待估计曲线为:
y = e x p ( a x 2 + b x + c ) + w w 为误差,满足高斯分布 y = exp(ax^2+bx+c)+w\qquad\qquad w为误差,满足高斯分布 y=exp(ax2+bx+c)+ww为误差,满足高斯分布
我们现在有很多 x i , y i x_i, y_i xi,yi 点,待估计变量为 a , b , c a, b, c a,b,c。
则我们要求解的最小二乘问题为:
min a , b , c 1 2 ∑ i = 1 N ( ∣ ∣ y i − e x p ( a x i 2 + b x i + c ) ∣ ∣ 2 ) \min\limits_{a,b,c} \;\frac{1}{2}\sum\limits_{i=1}^N\Big(||y_i-exp(ax_i^2+bx_i+c)||^2\Big) a,b,cmin21i=1∑N(∣∣yi−exp(axi2+bxi+c)∣∣2)
可以看到 y i y_i yi 和 x i x_i xi 已知,误差就是真实值和待估计曲线的估计值的残差。
1.3 C++实现
按照以下步骤来,基本是个通式(只有关键的几步): 仍然以 1.2 的例子进行
1. 定义代价函数
struct CURVE_FITTING_COST
{CURVE_FITTING_COST(double x, double y) : _x(x), _y(y) {}// 残差的计算template <typename T>bool operator()( // 重载括号运算符const T *const abc, // 模型参数,有3维T *residual) const // 残差{residual[0] = T(_y) - ceres::exp(abc[0] * T(_x) * T(_x) + abc[1] * T(_x) + abc[2]); // y-exp(ax^2+bx+c)return true;}const double _x, _y; // x,y数据
};
- 也就是这么构造cost_function,重要的是残差函数
residual[0]定义在重载小括号中, - 将其封装成这样的结构体后,加入cost_function后,残差函数是优化过程中后台调用的
2. 构建最小二乘问题
ceres::Problem problem;for (int i = 0; i < N; i++){problem.AddResidualBlock( new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(new CURVE_FITTING_COST(x_data[i], y_data[i])), nullptr, abc );}
- 不同问题,构建的形式也是很固定的,首先创建
problem对象 - 依次向
problem对象中添加误差项。具体的: AddResidualBlock函数的三个参数分别为cost_function类,核函数,待估计参数的地址。不同的是,这里的cost_function类用的是模板类AutoDiffCostFunction,详细解释下这个AutoDiffCostFunctionAutoDiffCostFunction的模板参数为:函数结构体类型CostFunctor,待估计参数块的维度,待估计参数块的数量- 在 Ceres 中,
cost_function结构体的实例必须通过ceres::AutoDiffCostFunction或ceres::NumericDiffCostFunction对象来进行封装,以便 Ceres 能够自动计算其梯度 - Ceres 会自动计算残差函数关于每个参数块的偏导数,从而得到残差函数的梯度。
3. 配置求解器,开始优化
//配置求解器,这里有很多options的选项,自查
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR; //增量方程如何求解,QR分解的方法
options.minimizer_progress_to_stdout = true; //输出到命令行ceres::Solver::Summary summary; // 优化信息
ceres::Solve(options, &problem, &summary); // 开始优化
- options求解器配置还有很多选项,自行了解
- 将其输出到命令行,保存迭代信息
4. 优化完毕,查看结果
cout << summary.BriefReport() << endl;cout << "estimated a,b,c = ";for (auto i : abc)cout << i << " ";cout << endl;
- summary中包含迭代次数,误差等信息
- 迭代完成后,数值会保存在待优化变量中,查看即可
2. G2O(General Graphic Optimization)
2.1 图优化
直观的观察到优化问题的样貌。
- 顶点(Vertex): 优化变量
- 边(Edge): 误差项
一个简单的图的例子:
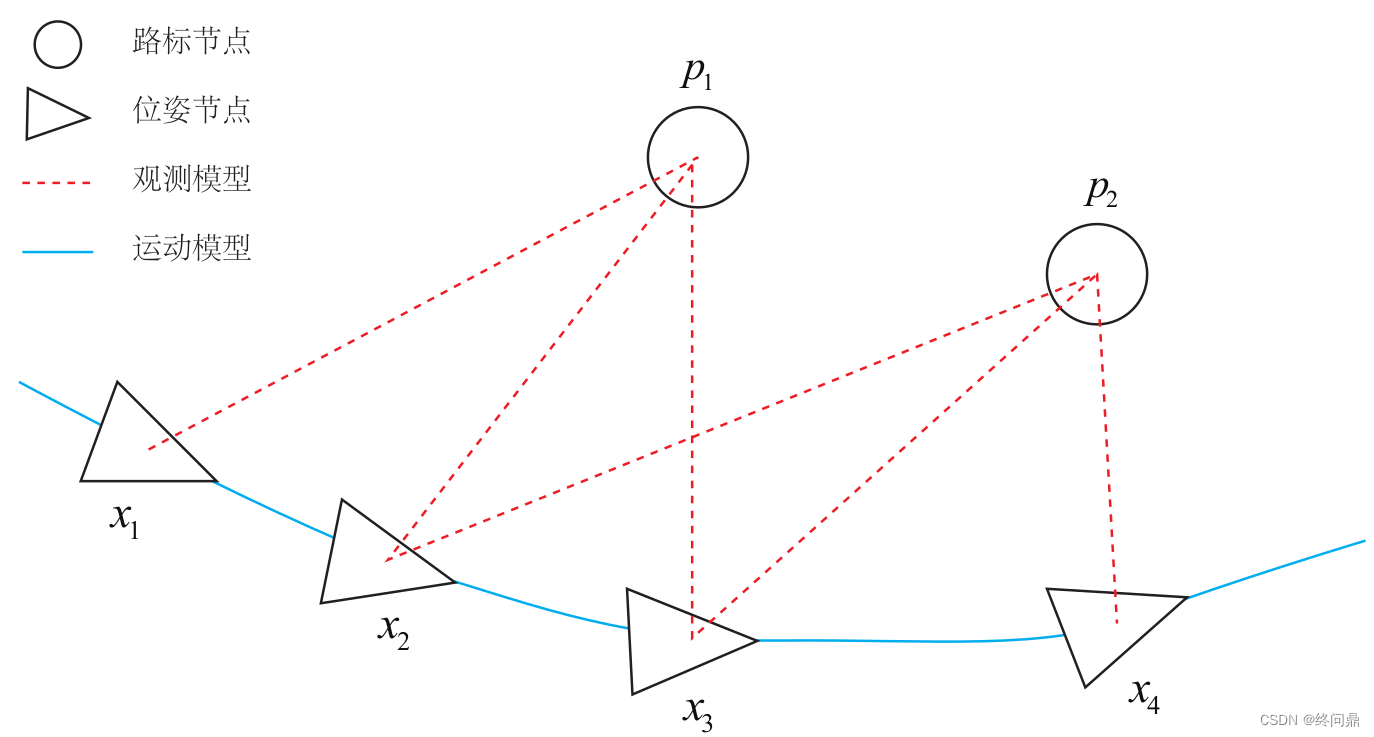
图优化的边:
- 蓝色线相机运动模型
- 红色虚线观测模型
2.2 具体例子
我们要求解的最小二乘问题为:
min a , b , c 1 2 ∑ i = 1 N ( ∣ ∣ y i − e x p ( a x i 2 + b x i + c ) ∣ ∣ 2 ) \min\limits_{a,b,c} \;\frac{1}{2}\sum\limits_{i=1}^N\Big(||y_i-exp(ax_i^2+bx_i+c)||^2\Big) a,b,cmin21i=1∑N(∣∣yi−exp(axi2+bxi+c)∣∣2)
我们的问题是曲线拟合问题,需要把它抽象成图优化的图。原则:节点为优化变量,边为误差项。则,不难将图优化为如下的样子:
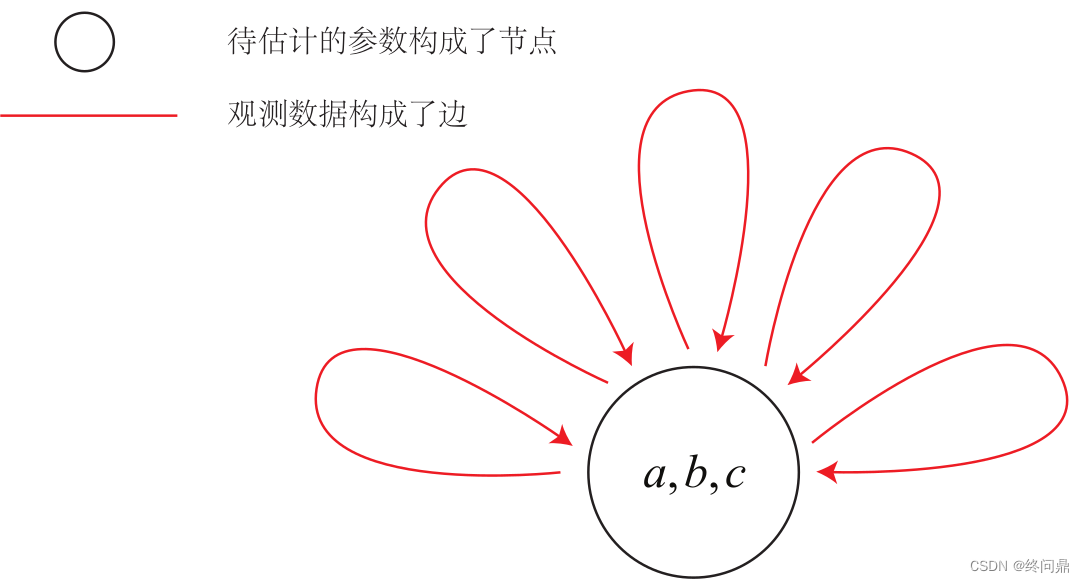
- 整个问题只有一个顶点:曲线模型参数 a , b , c a, b, c a,b,c
- 都是一元边: 每个数据点构成了一个个误差项
2.3 C++实现
按照以下步骤来,基本是个通式(只有关键的几步): 仍然以 2.2 的例子进行
1. 定义顶点
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWvirtual void setToOriginImpl() // 重置{_estimate << 0,0,0;}virtual void oplusImpl( const double* update) // 更新{_estimate += Eigen::Vector3d(update);}
};
EIGEN_MAKE_ALIGNED_OPERATOR_NEW的加入是解决字节对其问题,具体看Eigen字节对其- 第一个函数是第一次给初始值
- 第二个函数是以后更新的过程
- 该函数是顶点基函数的共有继承类,
<3, Eigen::Vector3d>模板中给出了<优化变量维度, 数据类型> oplusImpl函数很重要,是增量 Δ x \Delta x Δx的计算,即 x k + 1 = x k + Δ x x_{k+1} = x_k + \Delta x xk+1=xk+Δx 的过程
2. 定义边
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW
1. CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}// 计算曲线模型误差void computeError(){
2. const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);
3. const Eigen::Vector3d abc = v->estimate();
4. _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ; }virtual bool read( istream& in ) {}virtual bool write( ostream& out ) const {}
public:double _x;
};
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>是基类一元边的共有继承,模板<1,double,CurveFittingVertex>中的内容分别是观测值维度,观测值类型,该边要连接的顶点类型(也就是上边1.中定义的)2.代码static_cast是强制类型转换符,将顶点转成我们自定义支持的类型3.代码表示提取当前值,estimate()就是查看现在V中的值4.代码就是误差,由于我们只有一个顶点,所以过程略微简单些
3. 配置求解器
typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block;
- BlockSolver类模板的使用了3X3的稠密矩阵块储存海森矩阵,每个块的大小为1X1的求解器
- 每个误差项优化变量维度(顶点参数数量)为3,误差值维度为1
std::unique_ptr<Block::LinearSolverType> linearSolver ( new g2o::LinearSolverDense<Block::PoseMatrixType>());
- 线性方程求解器
LinearSolverType是线性求解器的类型:用于指定解线性方程的算法。 - 用
new创建LinearSolverDense实例,是G2O库中用于求解稠密矩阵的线性求解器,PoseMatrixType指定了矩阵块的类型,也就是上边BlockSolverTraits中的类型 - 最后
linearSolver现在是一个std::unique_ptr(Block::LinearSolverType)对象,它有一个LinearSolverDense类的实例 LinearSolverDense是LinearSolverType类的一种实现
std::unique_ptr<Block> solver_ptr (new Block ( std::move(linearSolver)));// 梯度下降方法,从GN, LM, DogLeg 中选
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( std::move(solver_ptr));
- 还可以用其他方法,如下两句替换上边的也可以
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( std::move(solver_ptr));
g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( std::move(solver_ptr));
4. 配置图模型
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm( solver ); // 设置求解器
optimizer.setVerbose( true ); // 打开调试输出
// 往图中增加顶点
CurveFittingVertex* v = new CurveFittingVertex();
//设置位姿估计值,V一个位姿估计器(pose estimater),这里是0初始位姿
v->setEstimate( Eigen::Vector3d(0,0,0) );
//区分不同的位姿估计器,一个估计器一个id
v->setId(0);optimizer.addVertex(v);
- 除最后一句,其他的都是将顶点按照图要求的配置
- 最后一句将
v加入图中,告诉优化器应该优化该机器人的pose
5. 向图添加边
for ( int i=0; i<N; i++ ){
1. CurveFittingEdge* edge = new CurveFittingEdge(x_data[i]); //残差做边
2. edge->setId(i); // 该残差边的id
3. edge->setVertex(0, v); // 设置连接的顶点,v就是顶点,就是要优化的系数a,b,c,通过优化器估计顶点值
4. edge->setMeasurement(y_data[i]); // 观测数值y,也许是为了弥补构造函数中计算代价函数时候没有y(_measurement)的原因
5. edge->setInformation(Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma)); // 信息矩阵,也就是边的权重:协方差矩阵之逆,也就是高斯分布最大似然里边的那个
6. optimizer.addEdge(edge);}
1.残差做边2.设置该残差边的id3.设置连接的顶点v,即包含a,b,c的4.向边加入观测值/真实值 y(_measurement)5.设置该边的权重,也称信息矩阵6.边配置完毕,将该边加入图中。其实这个配置点和边,最后一步加入途中的步骤很像。
6. 执行优化
1. optimizer.initializeOptimization(); //对图模型初始化
2. optimizer.optimize(100); //最大迭代次数,每次迭代会更新顶点
1.初始化图模型,为顶点和边分配内存空间2.对图模型进行优化,设置最大迭代次数为100.每次迭代都会更新图模型中的顶点
7. 查看
Eigen::Vector3d abc_estimate = v->estimate();
cout<<"estimated model: "<<abc_estimate.transpose()<<endl;
3. 总结
- 实际上G2O并不是用来做曲线拟合的,在SLAM中带有多个相机位姿和空间点较为复杂,在G2O中有很好的定义,而CERES中需要自己实现
Cost function - 基本处理这种东西,该库是通式,多看两遍就熟悉了
- 在G2O的顶点定义中有 Δ x \Delta x Δx 的计算,但是在SLAM中,它不仅仅是数值的加法,要用到李群李代数的左乘或者右乘更新了。
本节主要介绍了非线性优化问题:许多个误差项平方组成的最小二乘问题。(SLAM中较为常见)
相关文章:

【视觉SLAM入门】4.3. (非线性最小二乘问题)优化算法实现-ceres和g2o, 图优化理论
"天道不争而善胜" 1. Ceres库1.1 名词解释1.2 具体例子1.3 C实现1. 定义代价函数2. 构建最小二乘问题3. 配置求解器,开始优化4. 优化完毕,查看结果 2. G2O(General Graphic Optimization)2.1 图优化2.2 具体例子2.3 C实现1. 定义顶点2. 定义边…...

vue Can‘t resolve ‘path‘
BREAKING CHANGE: webpack < 5 used to include polyfills for node.js core modules by default. This is no longer the case. Verify if you need this module and configure a polyfill for it. 这句话的意思是webpack 5之前是自动导入node一些核心模块的垫片…...

【JavaEE初阶】——第七节.Servlet入门学习笔记
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:JavaEE进阶 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!! 文章目录 前…...
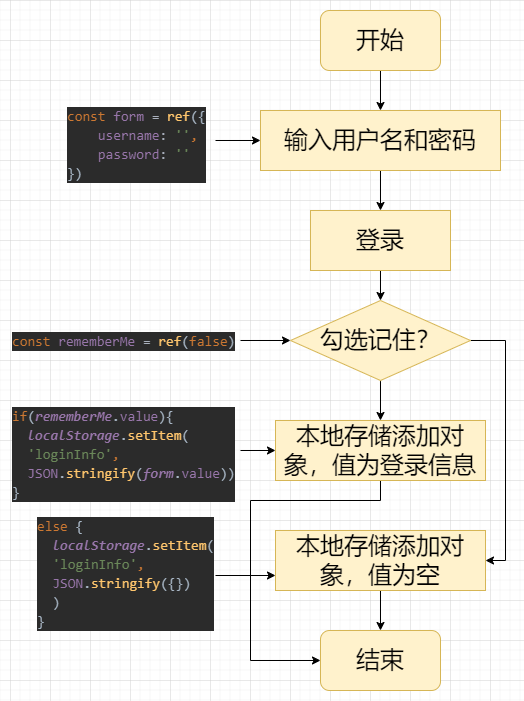
vue项目登录页面实现记住用户名和密码
vue项目登录页面实现记住用户名和密码 记录一下实现的逻辑,应该分两步来理解这个逻辑 首次登录,页面没有用户的登录信息,实现逻辑如下: 用户输入用户名和密码登录,用户信息为名为form的响应式对象,v-model…...
数学建模-MATLAB三维作图
导出图片用无压缩tif会更清晰 帮助文档:doc 函数名 matlab代码导出为PDF 新建实时脚本或右键文件转换为实时脚本实时编辑器-全部运行-内嵌显示保存为PDF...

pytorch工具——使用pytorch构建一个神经网络
目录 构建模型模型中的可训练参数假设输入尺寸为32*32损失函数反向传播更新网络参数 构建模型 import torch import torch.nn as nn import torch.nn.functional as Fclass Net(nn.Module):def __init__(self):super(Net,self).__init__()#定义第一层卷积层,输入维…...
)
在CSDN学Golang云原生(Kubernetes Pod)
一,pod的定义与基本用法 在 Kubernetes 中,Pod 是最小的可部署单元,它包含一个或多个容器。使用 Golang 来定义和操作 Pod 时,需要使用 kubernetes/client-go 包提供的 API。 以下是 Golang 定义和基本用法 Pod 的示例ÿ…...

我开源了团队内部基于SpringBoot Web快速开发的API脚手架v1.7.0更新
什么是 rest-api-spring-boot-starter rest-api-spring-boot-starter 适用于SpringBoot Web API 快速构建让开发人员快速构建统一规范的业务RestFull API 不在去关心一些繁琐。重复工作,而是把重点聚焦到业务。 动机 每次Web API常用功能都需要重新写一遍。或者复…...
excel要如何自动累加某个单元格上方的所有单元格?
输入公式 SUM(INDIRECT("A1:A"&ROW()-1)) 运行实例如下图 注意图中b4,和b5单元格都输入相同的公式。 此方法可以避免写vba,以前此类问题的解决都是通过vba代码进行处理 对函数进行解析 主要使用了 INDIRECT() 2、公式说明:…...

广州道可维斯受邀参加首届金蝶暨佛山数字化生态峰会
2023首届金蝶暨佛山数字化生态峰会,于7月28日在佛山隆重举行。此次大会由金蝶软件集团主办,共有超150家软件行业企业莅临参与,共同探讨数字化行业的最新动态和趋势。 活动当日,道可维斯的客户成功中心主任梁健,做了以“企业内容管…...

ubuntu远程控制小车 运行rviz时报错
我买的是wheeltec的小车,测试rgbd相机时想在ubuntu上的rviz中显示小车的姿态和看到的rgb和depth图,但是ubuntu中rostopic list和rviz都找不到小车发布的话题信息,运行rqt_image_view时可以显示图片信息。 最终wheeltec的技术人员lucas帮我找了…...

轻松实现自定义数据脱敏返回
学习目标: 实现简单的数据脱敏功能 例如: 学习自定义数据脱敏 学习内容: 使用到:泛型、反射 /*** * param obj 需要数据脱敏的对象* param par 那些字段需要脱敏* param <T>* return* throws Exception*/public static …...
函数)
pytorch 中_call_impl()函数
记录pytorch 版本中的 nn.Module() 重要函数 1. _call_impl() 1.1 torch1.7.1 版本 def _call_impl(self, *input, **kwargs):for hook in itertools.chain(_global_forward_pre_hooks.values(),self._forward_pre_hooks.values()):result hook(self, input)if result is n…...

openGauss学习笔记-22 openGauss 简单数据管理-HAVING子句
文章目录 openGauss学习笔记-22 openGauss 简单数据管理-HAVING子句22.1 语法格式22.2 参数说明22.3 示例 openGauss学习笔记-22 openGauss 简单数据管理-HAVING子句 HAVING子句可以让我们筛选分组后的各组数据。 WHERE子句在所选列上设置条件,而HAVING子句则在由…...
干货 | 常见电路板GND与外壳GND之间接一个电阻一个电容,为什么?
干货 | 常见电路板GND与外壳GND之间接一个电阻一个电容,为什么? 外壳是金属的,中间是一个螺丝孔,也就是跟大地连接起来了。这里通过一个1M的电阻跟一个0.1uF的电容并联,跟电路板的地连接在一起,这样有什么好…...

网络层协议总览
网络层协议总览 IPARP(地址解析协议)ICMP(网际控制报文协议)路由选择协议NAT(网络地址转换协议) 网络层的主要协议包括IP、ARP、RARP、ICMP、IGMP以及各种路由选择协议等。 IP IP协议是TCP/IP协议簇中的核…...

C++模拟实现list
1.首先要了解到vs底层的list链表是带头双向循环的链表。 所以首先就要看成员变量 那么就说明我们还需要构造一个Node的结构体,(typedef一下就好了,名字不影响) 现在就可以完成间的push_back函数了。 1.list的iterator 我们之前模…...

PostgreSQL PG16 逻辑复制在STANDBY 上工作 (译)
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...

《零基础入门学习Python》第058讲:论一只爬虫的自我修养6:正则表达式2
上一节课我们通过一个例子(匹配 ip 地址)让大家初步了解到正则表达式的魔力,也让大家充分了解到学习正则表达式是一个相对比较困难的事情。所以这一节课我们将继续学习 正则表达式的语法。 我们依稀还记得在Python中,正则表达式是…...
第一堂棒球课:MLB棒球大联盟的主要战术·棒球1号位
MLB棒球大联盟的主要战术 攻击战术run-and-foul(跑垒战术):以速度为优势,在适当的时机发动进攻,争取在一回合内完成得分。 grounder(阻截战术):队员在垒包之间阻止对手的跑垒和传球。…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
