论文笔记--Skip-Thought Vectors
论文笔记--Skip-Thought Vectors
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
- 3.1 Skip Thought Vectors
- 3.2 词表拓展
- 4. 文章亮点
- 5. 原文传送门
- 6. References
1. 文章简介
- 标题:Skip-Thought Vectors
- 作者:Ryan Kiros, Yukun Zhu, Ruslan Salakhutdinov, Richard S. Zemel, Antonio Torralba, Raquel Urtasun, Sanja Fidler
- 日期:2015
- 期刊:NIPS
2. 文章概括
文章提出了Skip Thought模型,旨在提供一种句向量的预训练方式。文章的核心思想类似于Word2Vec的skip-gram方法,即通过当前句子预测上下文句子。整体架构如下

3 文章重点技术
3.1 Skip Thought Vectors
文章的整体架构选用基于GRU的encoder-decoder网络架构。给定输入的句子三元组 ( s i − 1 , s i , s i + 1 ) (s_{i-1}, s_{i}, s_{i+1}) (si−1,si,si+1),令 w i t w_i^t wit表示句子 s i s_i si的第 t t t个单词, x i t x_i^t xit表示其对应的单词嵌入。
首先模型对输入的句子 s i s_i si进行编码,encoder国策可表示为下面的GRU公式: r t = σ ( W r x t + U r h t − 1 ) ∈ ( 0 , 1 ) , z t = σ ( W z x t + U z h t − 1 ) ∈ ( 0 , 1 ) , h ‾ t = tanh ( W x t + U ( r t ⊙ h t − 1 ) ) , h t = ( 1 − z t ) ⊙ h t − 1 + z t ⊙ h ‾ t r^t = \sigma (W_r x^t + U_r h^{t-1}) \in (0, 1), \\z^t = \sigma (W_z x^t + U_z h^{t-1}) \in (0, 1), \\\overline{h}^t = \tanh (Wx^t + U(r^t \odot h^{t-1})) ,\\ h^t = (1-z^t)\odot h^{t-1} + z^t \odot \overline{h}^t rt=σ(Wrxt+Urht−1)∈(0,1),zt=σ(Wzxt+Uzht−1)∈(0,1),ht=tanh(Wxt+U(rt⊙ht−1)),ht=(1−zt)⊙ht−1+zt⊙ht,其中 r t , z t ∈ ( 0 , 1 ) r^t, z^t \in (0, 1) rt,zt∈(0,1)表示重置门和更新门, h ‾ t \overline{h}^t ht表示候选的隐藏状态,其更新到 t t t时刻的隐藏层比例由更新门 z t z^t zt确定,其从上一个时刻隐藏层输入的比例由重置门 r t r^t rt确定。
接下来将句子编码分别传入到解码GRU中,用于预测当前句子相邻的上/下一个句子 s i − 1 , s i + 1 s_{i-1}, s_{i+1} si−1,si+1,省略角标 i − 1 , i + 1 i-1, i+1 i−1,i+1,相邻两个句子的解码公式均为 r t = σ ( W r d x t − 1 + U r d h t − 1 + C r h i ) ∈ ( 0 , 1 ) , z t = σ ( W z d x t + U z d h t − 1 ) + C z h i ∈ ( 0 , 1 ) , h ‾ t = tanh ( W d x t + U d ( r t ⊙ h t − 1 ) + C h i ) , h t = ( 1 − z t ) ⊙ h t − 1 + z t ⊙ h ‾ t r^t = \sigma (W_r^d x^{t-1} + U_r^d h^{t-1} + C_r h_i )\in (0, 1), \\z^t = \sigma (W_z^d x^t + U_z^d h^{t-1}) + C_z h_i \in (0, 1), \\\overline{h}^t = \tanh (W^dx^t + U^d(r^t \odot h^{t-1}) + Ch_i) ,\\ h^t = (1-z^t)\odot h^{t-1} + z^t \odot \overline{h}^t rt=σ(Wrdxt−1+Urdht−1+Crhi)∈(0,1),zt=σ(Wzdxt+Uzdht−1)+Czhi∈(0,1),ht=tanh(Wdxt+Ud(rt⊙ht−1)+Chi),ht=(1−zt)⊙ht−1+zt⊙ht,即计算当前时刻的解码输出时,会考虑上一时刻的输入词嵌入和当前时刻的编码输出 h i h_i hi。给定 h i + 1 t h_{i+1}^t hi+1t,训练目标为通过前面时刻的单词预测(输入单词及对应编码嵌入)当前时刻 t t t的单词: P ( w i + 1 t ∣ w i + 1 < t , h i ) ∝ exp ( v w i + 1 t , h i + 1 t ) P(w_{i+1}^t|w_{i+1}^{<t}, h_i) \propto \exp (v_{w_{i+1}^t}, h_{i+1}^t) P(wi+1t∣wi+1<t,hi)∝exp(vwi+1t,hi+1t),其中 v w i + 1 t v_{w_{i+1}^t} vwi+1t表示 w i + 1 t w_{i+1}^t wi+1t对应的词表矩阵的行向量。
总结来说,模型会首先对输入句子进行编码,然后将该编码得到的隐藏状态输入到其相邻句子的解码GRU中,尝试生成与其相邻的句子。类似于word2vec中的通过中心词预测上下文,只是上下文窗口固定为1。
最终训练的目标函数即为相邻句子解码的目标函数之和: ∑ t log P ( w i + 1 t ∣ w i + 1 < t , h i ) + log P ( w i − 1 t ∣ w i − 1 < t , h i ) \sum_t \log P(w_{i+1}^t|w_{i+1}^{<t}, h_i) + \log P(w_{i-1}^t|w_{i-1}^{<t}, h_i) t∑logP(wi+1t∣wi+1<t,hi)+logP(wi−1t∣wi−1<t,hi)
3.2 词表拓展
为了处理词表中未出现的单词,文章选择采用Word2Vec等较全的预训练单词嵌入进行补充。由于该单词嵌入和Skip-thought训练的单词嵌入有一定的偏差,所以文章先训练一个从Word2Vec到RNN(Skip-thought)的l2线性回归: f : V w 2 v → V r n n f: \mathcal{V}_{w2v}\to \mathcal{V}_{rnn} f:Vw2v→Vrnn。推理阶段,针对词表中未出现的单词 v v v,会首先查找其在Word2Vec下的嵌入 v w 2 v v_{w2v} vw2v,再通过学习好的映射 f f f预测其在文章训练的空间下的嵌入表达; v r n n ≈ f ( v w 2 v ) v_{rnn} \approx f(v_{w2v}) vrnn≈f(vw2v)。
4. 文章亮点
文章参考Skip-gram的思想,通过训练一个基于RNN的编码-解码模型,得到句子的预训练嵌入。实验证明,只需要在预训练的嵌入上增加一个简单的Logistic Regression,就可以持平针对下游任务精心设计的模型的表现,在当下(2015年)达到了SOTA水平。且文章通过t-SNE方法对训练的句向量进行了可视化表达,发现训练的句向量在多个数据集上呈现较为理想(按照标签组团)的分布,如下图所示。

文章给出的Skip-thought向量可以较好的捕捉到句子特征,可供开发人员在此基础上进一步研究基于句向量的NLP任务。
5. 原文传送门
Skip-Thought Vectors
6. References
[1] 论文笔记–Efficient Estimation of Word Representations in Vector Space
相关文章:

论文笔记--Skip-Thought Vectors
论文笔记--Skip-Thought Vectors 1. 文章简介2. 文章概括3 文章重点技术3.1 Skip Thought Vectors3.2 词表拓展 4. 文章亮点5. 原文传送门6. References 1. 文章简介 标题:Skip-Thought Vectors作者:Ryan Kiros, Yukun Zhu, Ruslan Salakhutdinov, Rich…...

1400*B. Karen and Coffee
Examples input 3 2 4 91 94 92 97 97 99 92 94 93 97 95 96 90 100 output 3 3 0 4 input 2 1 1 1 1 200000 200000 90 100 output 0 解析: 题意为,给你多个区间(会有重叠),每个区间的每个值都会为这个值累加…...

【业务功能篇54】Springboot项目常用工具类:HTTP状态码/客户端request
状态码常量类 /*** 返回状态码**/ public class HttpStatus {/*** 操作成功*/public static final int SUCCESS 200;/*** 对象创建成功*/public static final int CREATED 201;/*** 请求已经被接受*/public static final int ACCEPTED 202;/*** 操作已经执行成功࿰…...

Fine Logic
登录—专业IT笔试面试备考平台_牛客网 题目大意:有n个数分别为1~n,有m个数值对(u,v)表示u要排在v左边,问至少要多少个排列才能满足所有数值对至少一次 2<n<1e6;1<m<1e6 思路:如果数值对中要求u在v左边,…...

Neo4j图数据基本操作
Neo4j 文章目录 Neo4jCQL结点和关系增删改查匹配语句 根据标签匹配节点根据标签和属性匹配节点删除导入数据目前的问题菜谱解决的问题 命令行窗口 neo4j.bat console 导入rdf格式的文件 :GET /rdf/ping CALL n10s.graphconfig.init(); //初始化 call n10s.rdf.import.fetch(&q…...
)
前端JavaScript面试100问(中)
31、http 的理解 ? HTTP 协议是超文本传输协议,是客户端浏览器或其他程序“请求”与 Web 服务器响应之间的应用层通信协议。HTTPS主要是由HTTPSSL构建的可进行加密传输、身份认证的一种安全通信通道。32、http 和 https 的区别 ? 1、https协议需要到ca申请证书&…...

Docker 安全及日志管理与https部署
容器的安全性问题的根源在于容器和宿主机共享内核。如果容器里的应用导致Linux内核崩溃,那么整个系统可能都会崩溃。与虚拟机是不同的,虚拟机并没有与主机共享内核,虚拟机崩溃一般不会导致宿主机崩溃。 Docker 容器与虚拟机的区别 虚拟机通…...

2.3 HLSL常用函数
一、函数介绍 函数图像参考网站:Graphtoy 1.基本数学运算 函数 含义 示例图 min(a,b) 返回a、b中较小的数值 mul(a,b) 两数相乘用于矩阵计算 max(a,b) 返回a、b中较大的数值 abs(a) 返回a的绝对值 round(x) 返回与x最近的整数 sqrt(x) 返回x的…...

互联网的发展
概述 互联网是现代社会中举足轻重的一个领域,它的发展对于人类的生活和工作方式产生了深远的影响。互联网的发展经历了几个阶段,从初创阶段到如今的高度普及和深入应用,本文将详细介绍互联网的发展状况。 第一阶段:互联网的起源…...
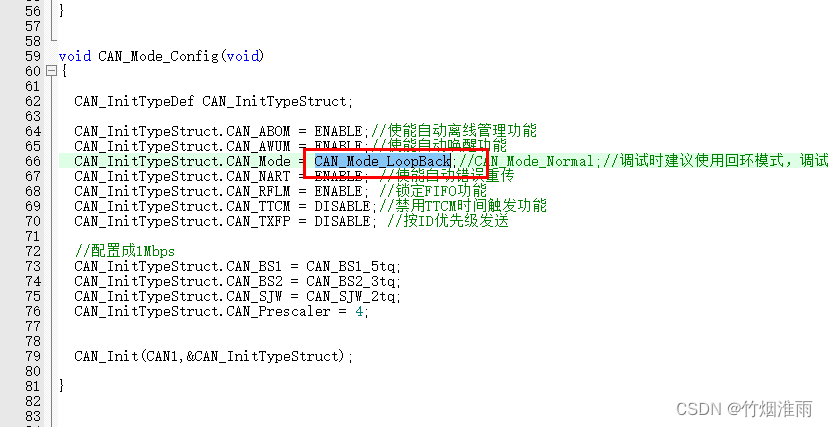
STM32 CAN通讯实验程序
目录 STM32 CAN通讯实验 CAN硬件原理图 CAN外设原理图 TJA1050T硬件描述 实验线路图 回环实验 CAN头文件配置 CAN_GPIO_Config初始化 CAN初始化结构体 CAN筛选器结构体 接收中断优先级配置 接收中断函数 main文件 实验现象 补充 STM32 CAN通讯实验 CAN硬件原理图…...

Python代码片段之Django静态文件URL的配置
首先要说明这段python代码并不完整,而且我也没有做过测试,只是我在工作时参考了其中的一些个方法。这是我在找python相关源码资料里看到的一段代码,是Django静态文件URL配置代码片段2,代码中有些方法还是挺技巧的,做其…...

基于飞桨paddle的极简方案构建手写数字识别模型测试代码
基于飞桨paddle的极简方案构建手写数字识别模型测试代码 原始测试图片为255X252的图片 因为是极简方案采用的是线性回归模型,所以预测结果数字不一致 本次预测的数字是 [[3]] 测试结果: PS E:\project\python> & D:/Python39/python.exe e:/pro…...

soft ip与hard ip
ip分soft和hard两种,soft就是纯代码,买过来要自己综合自己pr。hard ip如mem和analog与工艺有关。 mem的lib和lef是memory compiler产生的,基于bitcell,是foundry给的。 我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起…...
MyBatisPlus从入门到精通-2
接着上一讲的Mp的分页功能 下面我们讲解条件查询功能和其他功能 解决一下日志输出和banner问题 每次卞就会输出这些日志 很不美观,现在我们关闭一下 这样建个xml,文件名为logback.xml 文件内容改成这样 配置了logback但是里面什么都没写就不会说有日…...
)
AI面试官:Asp.Net 中使用Log4Net (一)
AI面试官:Asp.Net 中使用Log4Net (一) 当面试涉及到使用log4net日志记录框架的相关问题时,通常会聚焦在如何在.NET或.NET Core应用程序中集成和使用log4net。以下是一些关于log4net的面试题目,以及相应的解答、案例和代码: 文章目…...

Selenium自动化元素定位方式与浏览器测试脚本
Selenium八大元素定位方法 Selenium可以驱动浏览器完成各种操作,比如模拟点击等。要想操作一个元素,首先应该识别这个元素。人有各种的特征(属性),我们可以通过其特征找到人,如通过身份证号、姓名、家庭住…...

人机交互与人机混合智能的区别
人机交互和人机融合智能是两个相关但不完全相同的概念: 人机交互是指人与计算机之间的信息交流和互动过程。它关注的是如何设计和实现用户友好的界面,以便人们能够方便、高效地与计算机进行沟通和操作。人机交互通常强调用户体验和界面设计,旨…...

【项目】轻量级HTTP服务器
文章目录 一、项目介绍二、前置知识2.1 URI、URL、URN2.2 CGI2.2.1 CGI的概念2.2.2 CGI模式的实现2.2.3 CGI的意义 三、项目设计3.1 日志的编写3.2 套接字编写3.3 HTTP服务器实现3.4 HTTP请求与响应结构3.5 EndPoint类的实现3.5.1 EndPoint的基本逻辑3.5.2 读取请求3.5.3 构建响…...

sketch如何在线打开?有没有什么软件可以辅助
Sketch 在线打开的方法有哪些?这个问题和我之前回答过的「Sketch 可以在线编辑吗?」是一样的答案,没有。很遗憾,Sketch 没有在线打开的方法,Sketch 也做不到可以在线编辑。那么,那些广告里出现的设计软件工…...

CSS Flex 笔记
1. Flexbox 术语 Flex 容器可以是<div> 等,对其设置属性:display: flex, justify-content 是沿主轴方向调整元素,align-items 是沿交叉轴对齐元素。 2. Cheatsheet 2.1 设置 Flex 容器,加粗的属性为默认值 2.1.1 align-it…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
