打卡一个力扣题目
目录
一、问题
二、解题办法一
三、解题方法二
四、对比分析
关于 ARTS 的释义 —— 每周完成一个 ARTS:
● Algorithm: 每周至少做一个 LeetCode 的算法题
● Review: 阅读并点评至少一篇英文技术文章
● Tips: 学习至少一个技术技巧
● Share: 分享一篇有观点和思考的技术文章
希望通过此次活动能聚集一波热爱技术的人,延续好奇、探索、实践、分享的精神。
一、问题
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
二、解题办法一
def max_profit(prices):if not prices:return 0min_price = prices[0]max_profit = 0for price in prices:min_price = min(min_price, price)profit = price - min_pricemax_profit = max(max_profit, profit)return max_profit
这段代码实现了一个函数 `max_profit`,用于计算在给定的股票价格数组中,选择某一天买入并在未来某一个不同的日子卖出所能获取的最大利润。
首先判断输入的价格数组是否为空,如果为空则直接返回 0。
然后定义两个变量 `min_price` 和 `max_profit`,分别表示当前遍历到的价格中的最低价格和最大利润。初始时将它们都设置为数组的第一个元素。
接下来使用循环遍历整个价格数组,对于每个遍历到的价格,先更新 `min_price` 为当前遍历到的价格和之前记录的最低价格中的较小值,这样可以保证后续计算利润时使用的是更小的价格。
然后计算当前遍历到的价格与 `min_price` 之间的差值,即当前可以选择的利润。将这个利润与之前记录的最大利润比较,取较大值作为新的 `max_profit`。
最后返回 `max_profit` 作为结果。
需要注意的是,这段代码的时间复杂度为 O(n),其中 n 是输入的价格数组的长度。
提示:可简单介绍学习打卡过程中遇到的困难和对应的解决方法~
三、解题方法二
以下是另一种解题思路,使用动态规划的方法实现。
def max_profit(prices):if not prices:return 0n = len(prices)dp = [[0] * 2 for _ in range(n)]dp[0][0] = -prices[0]dp[0][1] = 0for i in range(1, n):dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])return dp[n-1][1]这段代码中,我们定义了一个二维数组 `dp`,其中 `dp[i][j]` 表示在第 i 天买入并在第 j 天卖出所能获取的最大利润。由于题目要求选择某一天买入并在未来某一个不同的日子卖出,因此我们在计算 `dp[i][j]` 时需要同时考虑两种情况,即在第 i 天买入或在第 i-1 天买入。这样就得到了一个二维的动态规划状态转移方程。
首先初始化 `dp[0][0]` 为 `-prices[0]`,表示如果不进行任何操作,则第一天亏损了价格;初始化 `dp[0][1]` 为 0,表示如果在第一天买入,则第一天没有获得利润。
然后从第 1 天开始遍历到第 n-1 天,对于每个遍历到的天数 i,分别计算在第 i 天买入和在第 i-1 天买入所能获取的最大利润,并取其中的较大值作为当前状态的最优解。具体来说,如果在第 i 天买入,则 `dp[i][0]` 可以取到 `dp[i-1][1] - prices[i]`;如果在第 i-1 天买入,则 `dp[i][1]` 可以取到 `dp[i-1][0] + prices[i]`。最后返回 `dp[n-1][1]` 作为结果。
四、对比分析
这两种方法的时间复杂度都是 O(n),其中 n 是输入的价格数组的长度。因此它们的时间复杂度是相同的,都可以在较短的时间内解决问题。
但是从代码实现的角度来看,这两种方法有一些不同之处。第一种方法使用了循环遍历整个价格数组,并在遍历过程中不断更新最小价格和最大利润。这种方法比较直观,易于理解,但是当价格数组很大时,可能会导致内存占用过高。
第二种方法使用了动态规划的思想,将问题分解为若干个子问题,并通过状态转移方程求解出每个子问题的最优解。这种方法可以有效地减少重复计算,避免了空间复杂度过高的问题。同时,由于动态规划的状态转移方程较为简单,因此代码实现也相对简洁。
综上所述,两种方法各有优缺点,可以根据具体的情况选择适合的方法来解决问题。
相关文章:

打卡一个力扣题目
目录 一、问题 二、解题办法一 三、解题方法二 四、对比分析 关于 ARTS 的释义 —— 每周完成一个 ARTS: ● Algorithm: 每周至少做一个 LeetCode 的算法题 ● Review: 阅读并点评至少一篇英文技术文章 ● Tips: 学习至少一个技术技巧 ● Share: 分享一篇有观点…...
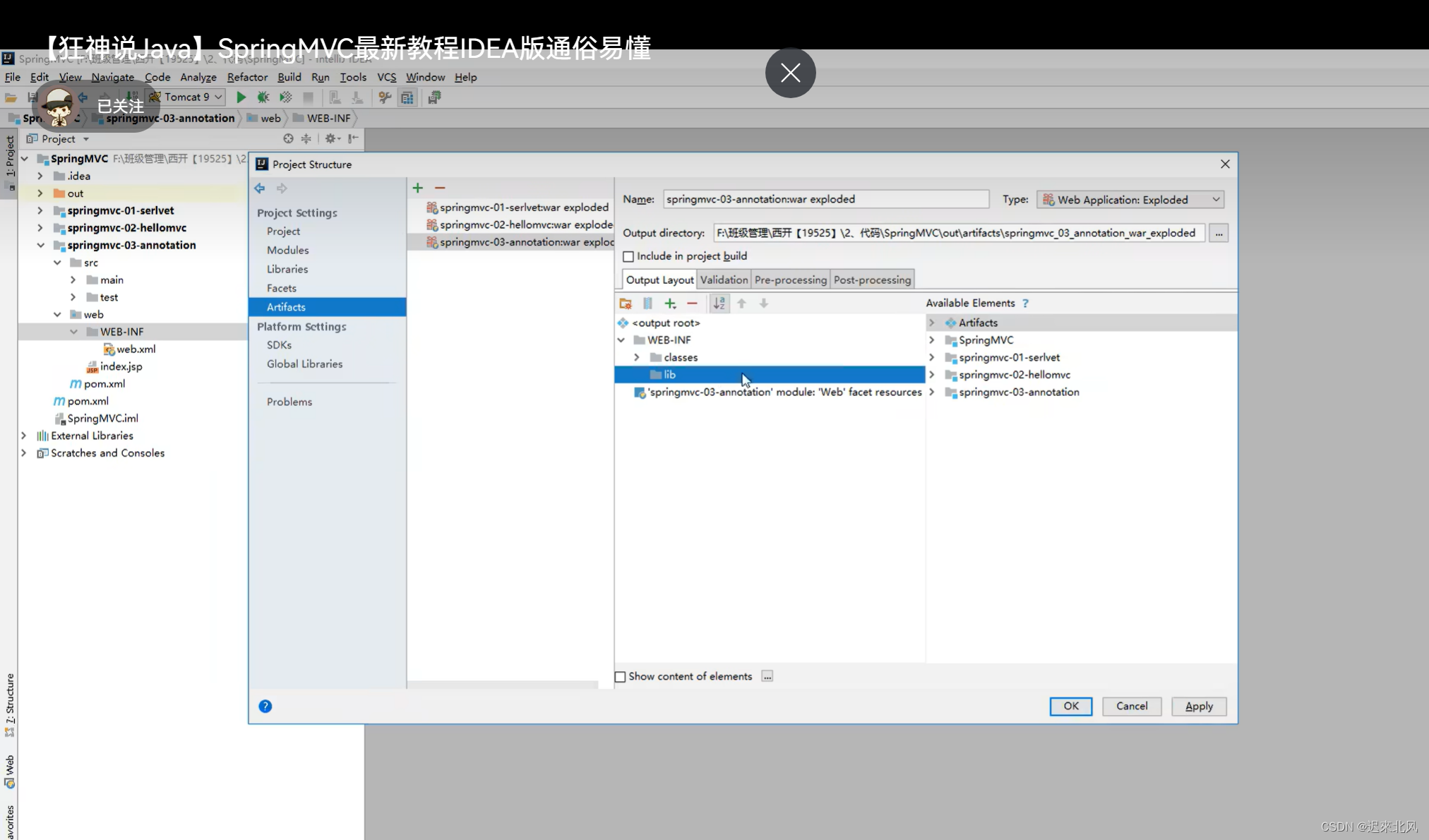
【SSM—SpringMVC】 问题集锦(持续更新)
目录 1.Tomcat启动,部署工件失败 1.Tomcat启动,部署工件失败 解决:使用SpringMVC,添加Web支持,要将项目结构进行添加WEB-INF下添加lib目录,将依赖添进去...
“软件测试”赛项接口测试任务书)
2022年全国职业院校技能大赛(高职组)“软件测试”赛项接口测试任务书
任务七 接口测试 执行接口测试 本部分按照要求,执行接口测试;使用接口测试工具PostMan,编写脚本、配置参数、执行接口测试并且截图,截图需粘贴在接口测试总结报告中。 接口测试具体要求如下: 题目1:资产…...
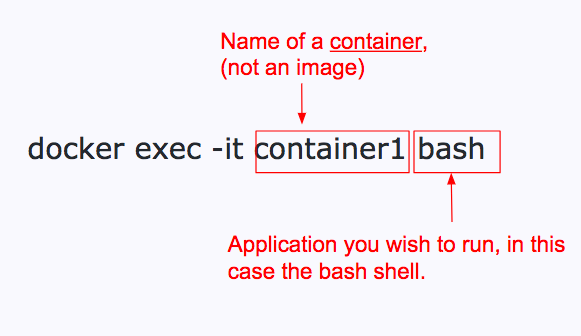
Docker 如何助您成为数据科学家
一、说明 在过去的 5 年里,我听到了很多关于 docker 容器的嗡嗡声。似乎我所有的软件工程朋友都在使用它们来开发应用程序。我想弄清楚这项技术如何使我更有效率,但我发现网上的教程要么太详细:阐明我作为数据科学家永远不会使用的功能&#…...

机器学习01 -Hello World(对鸢尾花(Iris Flower)进行训练及测试)
什么是机器学习? 机器学习是一种人工智能(AI)的子领域,它探索和开发计算机系统,使其能够从数据中学习和改进,并在没有明确编程指令的情况下做出决策或完成任务。 传统的程序需要程序员明确编写指令来告诉…...
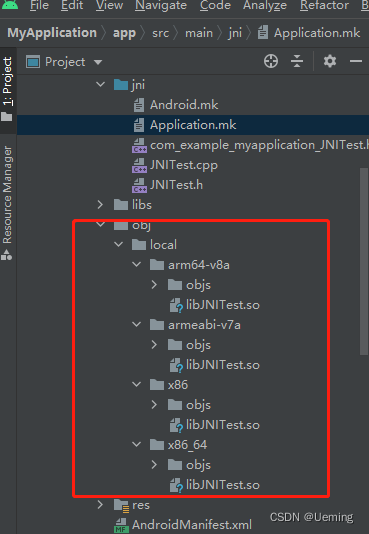
android studio JNI开发
一、JNI的作用: 1.使Java与本地其他类型语言(C、C)交互; 2.在Java代码调用C、C等语言的代码 或者 C、C调用Java代码。 由于JAVA具有跨平台的特点,所以JAVA与本地代码的交互能力弱,采用JNI特性可以增强JA…...
CSS 高频按钮样式
矩形与圆角按钮 正常而言,我们遇到的按钮就这两种 -- 矩形和圆角: 它们非常的简单,宽高和圆角和背景色。 <div classbtn rect>rect</div><div classbtn circle>circle</div>.btn {margin: 8px auto;flex-shrink: 0;…...
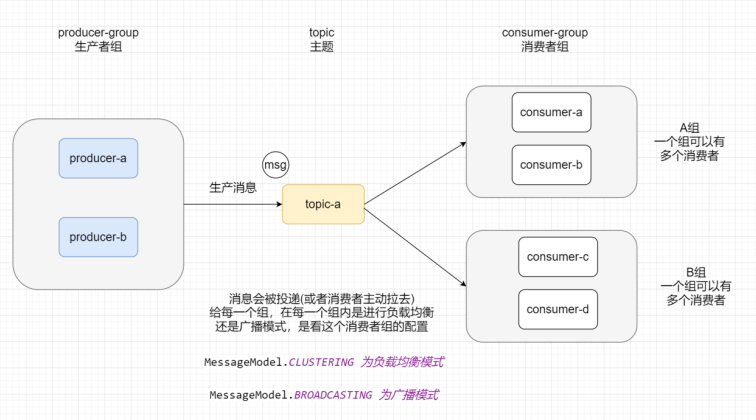
系列二、RocketMQ简介
一、概述 RocketMQ是一款阿里巴巴开源的消息中间件。2016年11月28日,阿里巴巴向Apache软件基金会捐赠RabbitMQ,成为Apache孵化项目。2017年9月25日,Apache宣布RocketMQ孵化成为Apache顶级项目(TLP),成为国内…...

论文笔记--Skip-Thought Vectors
论文笔记--Skip-Thought Vectors 1. 文章简介2. 文章概括3 文章重点技术3.1 Skip Thought Vectors3.2 词表拓展 4. 文章亮点5. 原文传送门6. References 1. 文章简介 标题:Skip-Thought Vectors作者:Ryan Kiros, Yukun Zhu, Ruslan Salakhutdinov, Rich…...

1400*B. Karen and Coffee
Examples input 3 2 4 91 94 92 97 97 99 92 94 93 97 95 96 90 100 output 3 3 0 4 input 2 1 1 1 1 200000 200000 90 100 output 0 解析: 题意为,给你多个区间(会有重叠),每个区间的每个值都会为这个值累加…...

【业务功能篇54】Springboot项目常用工具类:HTTP状态码/客户端request
状态码常量类 /*** 返回状态码**/ public class HttpStatus {/*** 操作成功*/public static final int SUCCESS 200;/*** 对象创建成功*/public static final int CREATED 201;/*** 请求已经被接受*/public static final int ACCEPTED 202;/*** 操作已经执行成功࿰…...

Fine Logic
登录—专业IT笔试面试备考平台_牛客网 题目大意:有n个数分别为1~n,有m个数值对(u,v)表示u要排在v左边,问至少要多少个排列才能满足所有数值对至少一次 2<n<1e6;1<m<1e6 思路:如果数值对中要求u在v左边,…...

Neo4j图数据基本操作
Neo4j 文章目录 Neo4jCQL结点和关系增删改查匹配语句 根据标签匹配节点根据标签和属性匹配节点删除导入数据目前的问题菜谱解决的问题 命令行窗口 neo4j.bat console 导入rdf格式的文件 :GET /rdf/ping CALL n10s.graphconfig.init(); //初始化 call n10s.rdf.import.fetch(&q…...
)
前端JavaScript面试100问(中)
31、http 的理解 ? HTTP 协议是超文本传输协议,是客户端浏览器或其他程序“请求”与 Web 服务器响应之间的应用层通信协议。HTTPS主要是由HTTPSSL构建的可进行加密传输、身份认证的一种安全通信通道。32、http 和 https 的区别 ? 1、https协议需要到ca申请证书&…...

Docker 安全及日志管理与https部署
容器的安全性问题的根源在于容器和宿主机共享内核。如果容器里的应用导致Linux内核崩溃,那么整个系统可能都会崩溃。与虚拟机是不同的,虚拟机并没有与主机共享内核,虚拟机崩溃一般不会导致宿主机崩溃。 Docker 容器与虚拟机的区别 虚拟机通…...

2.3 HLSL常用函数
一、函数介绍 函数图像参考网站:Graphtoy 1.基本数学运算 函数 含义 示例图 min(a,b) 返回a、b中较小的数值 mul(a,b) 两数相乘用于矩阵计算 max(a,b) 返回a、b中较大的数值 abs(a) 返回a的绝对值 round(x) 返回与x最近的整数 sqrt(x) 返回x的…...

互联网的发展
概述 互联网是现代社会中举足轻重的一个领域,它的发展对于人类的生活和工作方式产生了深远的影响。互联网的发展经历了几个阶段,从初创阶段到如今的高度普及和深入应用,本文将详细介绍互联网的发展状况。 第一阶段:互联网的起源…...
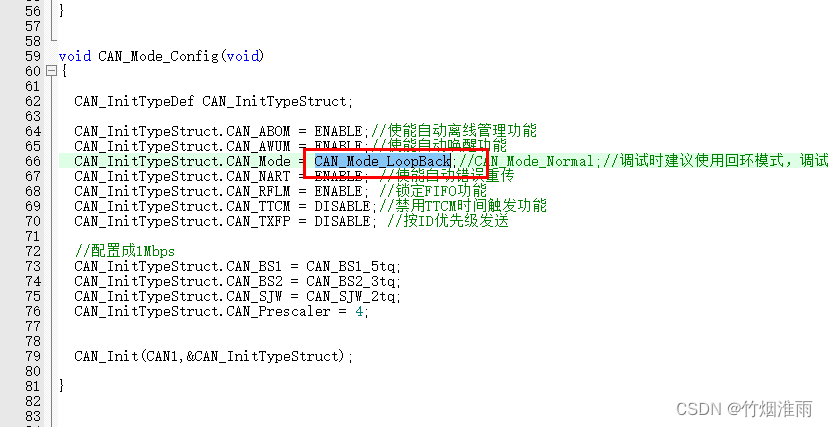
STM32 CAN通讯实验程序
目录 STM32 CAN通讯实验 CAN硬件原理图 CAN外设原理图 TJA1050T硬件描述 实验线路图 回环实验 CAN头文件配置 CAN_GPIO_Config初始化 CAN初始化结构体 CAN筛选器结构体 接收中断优先级配置 接收中断函数 main文件 实验现象 补充 STM32 CAN通讯实验 CAN硬件原理图…...

Python代码片段之Django静态文件URL的配置
首先要说明这段python代码并不完整,而且我也没有做过测试,只是我在工作时参考了其中的一些个方法。这是我在找python相关源码资料里看到的一段代码,是Django静态文件URL配置代码片段2,代码中有些方法还是挺技巧的,做其…...

基于飞桨paddle的极简方案构建手写数字识别模型测试代码
基于飞桨paddle的极简方案构建手写数字识别模型测试代码 原始测试图片为255X252的图片 因为是极简方案采用的是线性回归模型,所以预测结果数字不一致 本次预测的数字是 [[3]] 测试结果: PS E:\project\python> & D:/Python39/python.exe e:/pro…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
