【C++之容器篇】二叉搜索树的理论与使用
目录
- 前言
- 一、二叉搜索树的概念
- 二、二叉搜素树的模拟实现(增删查非递归实现)
- 1. 二叉搜素树的结点
- 2. 二叉搜索树的实现
- (1). 二叉搜索树的基本结构
- (2)构造函数
- (3)查找函数
- (4)插入函数
- (5) 删除函数
- (6)中序遍历
- (7)析构函数
- (8)拷贝构造函数
- (9)赋值运算符重载(现代写法)
- 三、二叉搜索树的模拟实现(增删查递归实现)
- 1. 查找函数
- 2. 插入函数
- 3. 删除函数
前言
在数据结构初阶我们学习了二叉树的相关知识,普通的二叉树的作用只是用来存储数据,并没有任何的性质,所以在任何方面都没有什么优势,今天学习的二叉搜索树是在普通的二叉树的基础上加上了一些性质,使整体的搜索效率大大提升。
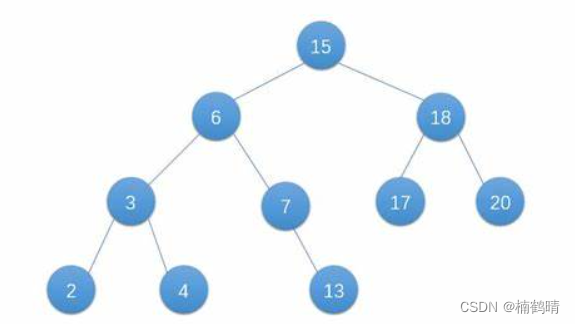
一、二叉搜索树的概念
二叉搜索树可能是一棵空树,也可能是一棵具有以下性质的二叉树:
- 如果左子树存在,则左子树所有结点的值都比根节点的值小
- 如果右子树存在,则右子树所有结点的值都比根节点的值大
- 树是递归创建的,所以二叉搜索树中的每一棵子树都要满足以上性质
二、二叉搜素树的模拟实现(增删查非递归实现)
1. 二叉搜素树的结点
// 二叉搜索树的结点
template <class K>
struct BSTreeNode
{// 成员函数//成员变量BSTreeNode<K>* _left;// 指向左孩子的指针(指针域)BSTreeNode<K>* _right;// 指向右孩子的指针(指针域)K _key;// 存储数据的地方(数据域)
};
二叉搜索树的结点中需要包含三个内容:
- _left:指向左孩子的结点的指针,通过这个指针找到左孩子,如果这个指针为空指针,说明当前这棵树不存在左子树
- _right:指向右孩子的结点的指针,通过这个指针找到右孩子,如果这个指针为空指针,说明当前这棵树不存在右子树
- _key:数据域,存放结点的数据的,一般也称为是二叉搜索树的关键字,二叉搜索树的性质就是以这个关键字为准的
2. 二叉搜索树的实现
(1). 二叉搜索树的基本结构
// 二叉搜素树的基本结构
template <class K>
class BSTree
{// 需要使用结点类型typedef BSTreeNode<T> Node;public:// 成员函数private:// 成员变量Node* _root = nullptr;
};
二叉搜索树的底层本质上就是一个根节点,然后通过这个根节点无限去创建其左右子树,在树中需要使用树的结点类型,所以为了方便表示,可以在树中对树的结点类型进行重定义(这个技巧在list的实现中也用到过)。刚开始_root的值默认为nullptr。
(2)构造函数
树不需要实现构造函数,只需要给_root一个缺省值即可。
(3)查找函数
// 查找函数bool find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_key;}else if(key>cur->_key){cur = cur->_right;}else{// 找到了return true;}}// 找不到return false;}
上面这个代码中是不需要单独判断树为空树的情况的,因为当树为空树的时候,那么_root = nullptr,此时cur = nullptr,所以循环压根不会进去,直接返回false。
(4)插入函数
// 插入函数bool insert(const K& key){if (_root == nullptr){// 空树_root = new Node(key);return true;}// 非空树// 找到插入的地方Node* cur = _root;// 找插入的位置Node* parent = nullptr;// 记录cur的父亲while (cur){if (key < cur->_key){// 左子树找parent = cur;cur = cur->_left;}else if (key > cur->_key){// 右子树找parent = cur;cur = cur->_right;}else{// 找到相等的值,不允许插入return false;}}// 当cur为空的时候,跳出循环,找到插入的位置cur = new Node(key);if (key < parent->_key){// 插在左子树parent->_left = cur;}else{parent->_right = cur;}return true;}
思路:
主题判断空树的情况,如果是空树,将结点直接插入在根,其他情况:先找到插入的位置,使用一个cur结点指针去标识找插入的位置,parent结点指针去记录cur的父亲结点,所以在cur找到了插入的位置之后,那么parent就是插入位置的父亲,查找的过程中,如果key的值比cur的值小,那么就是插入在左子树,如果key的值比cur的值大,那么就是插入在右子树,如果出现key的值和cur的值是相等的,则说明树中存在该值,不允许插入。最终当cur走到空的时候,则找到插入的位置,此时需要判断cur应该插入在parent的左边还是右边,可以通过插入的值和parent的值进行对比,如果插入的值比parent的值小,则插入在左子树,否则插入在右边。
- 测试查找和插入函数
代码:
void test_BSTree1()
{BSTree<int> t;t.insert(1);t.insert(3);t.insert(2);t.insert(6);t.insert(5);t.insert(9);// 查找cout << "1:" << t.find(1) << endl;cout << "2:" << t.find(2) << endl;cout << "3:" << t.find(3) << endl;cout << "4:" << t.find(4) << endl;cout << "5:" << t.find(5) << endl;cout << "6:" << t.find(6) << endl;}
运行结果:
(5) 删除函数
// 删除函数bool erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){// 找删除的值if (key < cur->_key){// 左子树找parent = cur;cur = cur->_left;}else if (key > cur->_key){// 右子树找parent = cur;cur = cur->_right;}else{// 找到了// 分类讨论// 1. 左孩子空:包含叶子节点// 2. 右孩子为空:不包含叶子节点// 3. 左右孩子都不为空if (cur->_left == nullptr){// 左子树为空,右子树不一定为空if (cur == _root){// cur就是根结点_root = cur->_right;}else{// cur不是根,cur的父亲结点是parentif (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){// 右子树为空,左子树一定不为空if (cur == _root){// cur是根节点_root = cur->_left;}else{// cur不是根节点,cur的父亲就是parentif (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 左子树和右子树都不为空// 找到删除结点所在树的右子树中的最小值Node* minRight = cur->_right;Node* minparent = cur;while (minRight->_left){minparent = minRight;minRight = minRight->_left;}swap(cur->_key, minRight->_key);if (minparent->_left == minRight){minparent->_left = minRight->_right;}else{minparent->_right = minRight->_right;}delete minRight;}return true;}}// cur走到空,说明树中不存在这个值,所以删除是被==失败return false;}
思路: 找到删除的值的结点,如果找不到,则删除失败,空树也是属于找不到的一种情况,如果找到了,需要对删除的结点进行分类讨论:
- 左孩子为空:不存在左子树,右子树是否存在不一定,可能存在也可能不存在,当右子树不存在的时候,此时该结点的左右子树均不存在,属于叶子结点
- 右孩子为空:此时左孩子一定不为空,因为左孩子为空的情况属于上面的请情况,所以这种情况的结点只存在右子树
- 左右孩子均不为空:同时存在左右子树的结点,需要采取替换法,然后转化为第一或者第二种情况进行删除。
细节:
- 在第一种情况和第二种情况中,删除的可能是根节点,当根节点没有左子树的时候,就属于第一种情况,当根节点没有右子树的时候,就属于第二种情况,如果删除的是根节点,该结点左子树为空时,则需要更新根节点到删除结点的右子树,该结点的右子树为空的时候,需要更新根节点到该节点的左子树。
- 第三种情况采取替换法,先找到删除的结点的左子树的最大值结点或者右子树的最小值结点,找这两种结点的原因是这个结点和删除的结点交换后可以保证该值比左子树的所有结点值都大,比右子树所有结点值都小。迭代的过程中一定要记录minRight的父亲,最终才能让该父亲去托管minRight的右子树,这个minparent一定是从删除的结点开始,因为minRight可能就是删除结点的右子树的根节点,这种情况就是删除结点的右子树的根节点没有左孩子的,此时循环是不会进去的,这种情况的minRight就是删除结点的右子树的根节点,那么其父亲就是删除的结点,所以在交换删除结点的值和minRight的值之后,问题就转化为删除minRight,此时minRight的左子树一定是空的,所以就算删除情况的第一种情况。
(6)中序遍历
// 中序遍历void InOrder(){// 因为在类外的对象不方便使用根节点,所以需要套一层进行递归_InOrder(_root);cout << endl;}// 中序遍历的子函数void _InOrder(Node* root){if (root == nullptr){return;}// 先遍历左子树_InOrder(root->_left);// 再访问根节点cout << root->_key << " ";// 最后遍历右子树_InOrder(root->_right);}
思路:在我们之前学习的二叉树的中序遍历中是直接进行递归的,因为C语言实现的二叉树并不是封装的,也就是对象可以直接访问树中的任何成员,但是C++不同,C++采用类对象进行封装的结构,类外的对象是不能访问类中的私有成员的,所以在类外不能访问到树的根节点,所以我们采取的方法就算套一层进行递归。递归的思路和之前一样:中序遍历就算先递归左子树,再访问根节点的值,再递归右子树。
(7)析构函数
二叉树中的结点都需要析构函数进行释放,所以析构函数需要我们自己实现,编译器形成析构函数无法完成这项工作。析构函数的实现思想同样采用递归的思路,而且采用的是后序递归,就是先将树的左子树递归,再递归右子树,最后将根节点释放。还有代码中的析构函数是public的,DestroyTree函数是私有的,析构函数是要给类外的对象进行使用的
public:
// 析构函数~BSTree(){DestroyTree(_root);}private:
void DestroyTree(Node* root){if (root == nullptr){// 空树return;}// 通过后序递归的方法将树中的每一个结点释放DestroyTree(root->_left);DestroyTree(root->_right);delete root;}
(8)拷贝构造函数
编译器默认生成的拷贝构造函数完成浅拷贝,如果采用拷贝,会导致两棵树中的根节点指针指向同一个根节点,也就是最终的两棵树是同一棵树,但是有两个对象,所以最终两个对象在生命周期到的时候都会调用析构函数清理资源,所以会出现同一棵树被清理两次,从而使程序崩溃。
void test_BSTree4()
{int a[] = { 2,3,7,1,5,9 };BSTree<int> t;for (auto& e : a){t.insert(e);}t.InOrder();cout << endl;BSTree<int> t1 = t;t1.InOrder();
}
运行结果:

- 深拷贝
代码:
// 拷贝构造函数
public:BSTree(const BSTree<K>& t){_root = copyTree(t._root);}private:
// copy函数Node* copyTree(const Node* root){if (root == nullptr){return nullptr;}Node* newnode = new Node(root->_key);newnode->_left = copyTree(root->_left);newnode->_right = copyTree(root->_right);return newnode;}
// 测试代码:
void test_BSTree4()
{int a[] = { 2,3,7,1,5,9 };BSTree<int> t;for (auto& e : a){t.insert(e);}t.InOrder();cout << endl;BSTree<int> t1 = t;// 调用拷贝构造函数t1.InOrder();
}
运行结果:

(9)赋值运算符重载(现代写法)
// 赋值运算符重载BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}void test_BSTree5()
{int a[] = { 2,3,7,1,5,9 };BSTree<int> t;for (auto& e : a){t.insert(e);}t.InOrder();cout << endl;BSTree<int> t1;t1 = t;// 调用赋值运算符重载t1.InOrder();
}
运行结果:

三、二叉搜索树的模拟实现(增删查递归实现)
1. 查找函数
public:// 递归版本bool FindR(const K& key){return _FindR(_root,key);}
private:// 查找函数的子函数(递归版本)bool _FindR(Node* root,const K& key){if (root == nullptr){// 空树return false;}// 非空树if (key < root->_key){// 左子树找return _FindR(root->_left, key);}else if (key > root->_key){// 右子树找return _FindR(root->_right, key);}else{// 找到了return true;}}
//测试代码:
void test_BSTree6()
{// 测试树的非递归查找函数int a[] = { 2,3,7,1,5,9 };BSTree<int> t;for (auto& e : a){t.insert(e);}t.InOrder();for (auto& e : a){cout << t.FindR(e) << " ";}
}运行结果:
2. 插入函数
public:
// 插入函数(递归版本)bool InsertR(const K& key){return _InsertR(_root, key);}
private:// 插入函数递归版本的子函数bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}// 查找插入的位置if (key < root->_key){// 插入在当前树的左子树return _InsertR(root->_left, key);}else if (key > root->_key){// 插入在当前树的右子树return _InsertR(root->_right, key);}else{// 该值在树中已经存在,插入失败return false;}}
// 测试代码
void test_BSTree7()
{// 测试插入函数的递归版本int a[] = { 2,3,7,1,5,9 };BSTree<int> t;for (auto& e : a){t.InsertR(e);}t.InOrder();}运行结果:

3. 删除函数
public:
// 删除函数的递归版本bool EraseR(const K& key){return _EraseR(_root, key);}
private:// 删除函数递归版本的子函数bool _EraseR(Node*& root, const K& key){if (root == nullptr){// 空树return false;}// 非空树,找删除的结点if (key < root->_key){// 到左子树找return _EraseR(root->_left, key);}else if (key > root->_key){// 到右子树找return _EraseR(root->_right, key);}else{// 找到了// 分类讨论Node* del = root;if (root->_left == nullptr){// 左子树为空root = root->_right;}else if (root->_right == nullptr){// 右子树为空root = root->_left;}else{// 左右子树均不为空// 替换法Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}swap(minRight->_key, root->_key);// 转化为第一种情况return _EraseR(root->_right, key);}delete del;return true;}}
// 测试代码:void test_BSTree8()
{// 测试插入函数的递归版本int a[] = { 2,3,7,1,5,9 };BSTree<int> t;for (auto& e : a){t.InsertR(e);}t.InOrder();t.EraseR(7);t.InOrder();t.EraseR(1);t.InOrder();for (auto& e : a){t.EraseR(e);}t.InOrder();
}运行结果:

相关文章:

【C++之容器篇】二叉搜索树的理论与使用
目录前言一、二叉搜索树的概念二、二叉搜素树的模拟实现(增删查非递归实现)1. 二叉搜素树的结点2. 二叉搜索树的实现(1). 二叉搜索树的基本结构(2)构造函数(3)查找函数(4…...

爬虫神级解析工具之XPath:用法详解及实战
一、XPATH是什么 Xpath最初被设计用来搜寻XML文档,但它同样适用于HTML文档的搜索。通过简洁明了的路径选择表达式,它提供了强大的选择功能;同时得益于其内置的丰富的函数,它可以匹配和处理字符串、数值、时间等数据格式,几乎所有节点我们都可以通过Xpath来定位。 在Pyth…...
Markdown编辑器
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注…...
数据结构<堆>
🎇🎇🎇作者: 小鱼不会骑车 🎆🎆🎆专栏: 《数据结构》 🎓🎓🎓个人简介: 一名专科大一在读的小比特,努力学习编程是我唯一…...
Linux下Socket编程利用多进程实现一台服务器与多台客户端并发通信
文章目录前言一、服务器 server二、客户端 client三、并发通信演示四、程序源码前言 前些日子同“ Linux应用编程 ”专栏中发布过的TCP及UDP在Linux或Windows下的通信都为单进程下的Socket编程,若还存在一些套接字相关函数模糊不清,读者可移步“Socket编…...

【MySQL】数据库基础
目录 1、什么是数据库 2、 数据库基本操作 2.1 查看当前数据库 2.2 创建一个数据库 2.3 选中数据库 2.4 删除数据库 3、常见的数据类型 3.1 数值类型 3.2 字符串类型 3.3 日期类型 4、表的操作 4.1 创建表 4.2 查看指定数据库下的所有表 4.3 查看表的结构 4.…...

Microsoft Office 2021 / 2019 Direct Download Links
前言 微软Office在很长一段时间内都是最常用和最受欢迎的软件。从小型创业公司到大公司,它的使用比例相当。它可以很容易地从微软的官方网站下载。但是,微软只提供安装程序,而不提供完整的软件供下载。这些安装文件通常比较小。下载并运行后,安装的文件将从后端服务器安装M…...

XX 系统oracle RAC+ADG 数据库高可用容灾演练记录
停止备库监听,避免强制关机时切换到备库 su - grid lsnrctl stop 主库高可用重启测试 /u01/app/19c/grid/bin/crsctl stop crs sync;sync;reboot --/u01/app/19c/grid/bin/crsctl start crs 机器重启后自动起的 /u01/app/19c/grid/bin/crsctl stat res -t 主库容…...
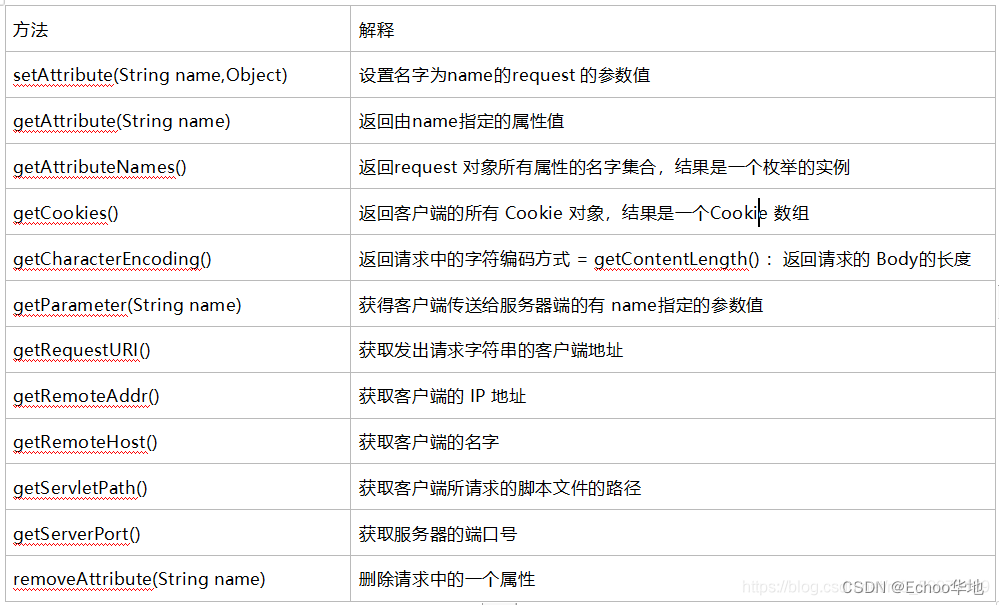
JSP与Servlet
一、什么是JSP? JSP(java Service Pages)是由Sun Microsystems公司倡导、许多公司参与一起建立的动态技术标准。 在传统的HTML文件(*.htm 、 *.html)中加入Java程序片段(Scriptlet)和JSP标签,构成了JSP网页。 1.1 JSP页面的运行原理 客户…...
C++之迭代器
迭代器C中,迭代器就是类似于指针的对象,但比指针的功能更丰富,它提供了对对象的间接访问,每个迭代器对象代表容器中一个确定的地址。举个例子:void test() {vector<int> vv{1,2,3,4,5};for(vector<int>::i…...
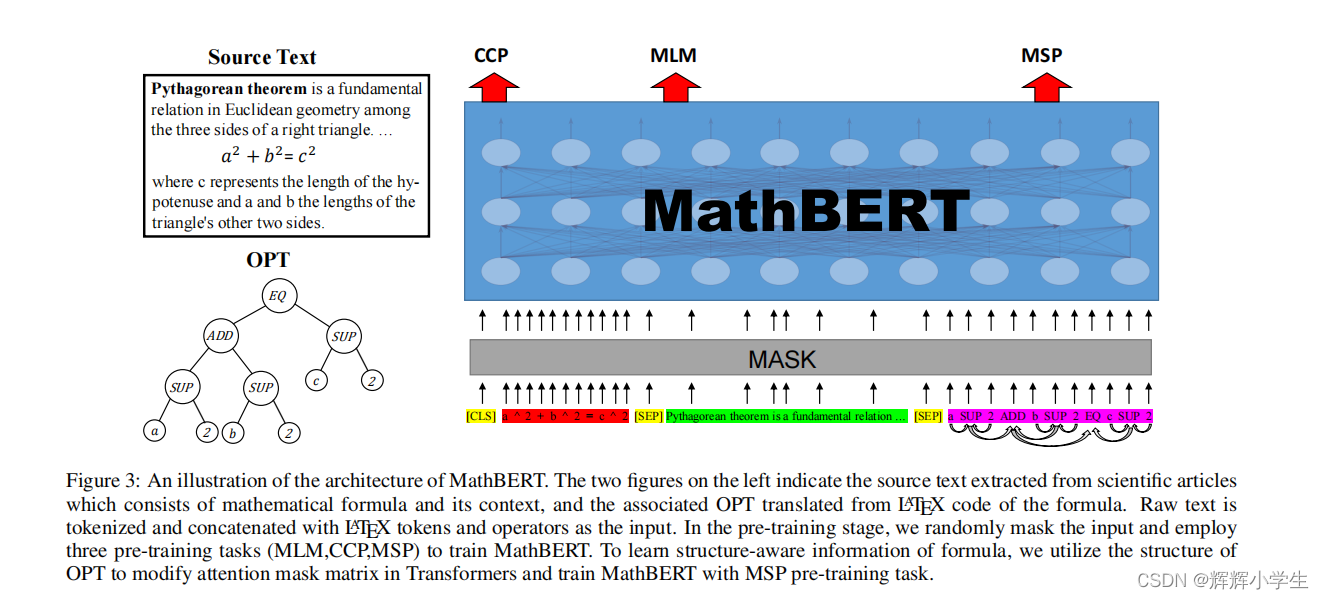
2023-02-16:干活小计
数学公式表示学习: 大约耗时:2 hours 在做了一些工作后重读论文:MathBERT: A Pre-Trained Model for Mathematical Formula Understanding 这是本篇论文最重要的idea:Current pre-trained models neglect the structural featu…...

Linux上安装LaTeX
Linux上安装LaTeX1. 安装1.1 下载安装texlive1.2 配置中文1.3 安装XeLatex1.4 安装编辑器1.5 设置默认支持中文编译1.6 配置环境路径2. latex配置2.1 latex自动安装宏包2.2 latex手动安装宏包2.2.1. 查找包2.2.2. 生成.sty文件2.2.3. 复制到配置文件夹3. 更新包3. 卸载参考链接…...
webpack -- 无法将“webpack”项识别为 cmdlet
webpack : 无法将“webpack”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写,如果包括路径,请确保路径正确,然后再试一次。 1.检测是否是版本太高而只能使用脚手架进行打包 webpack4.x的打包已经不能用webpack 文件a …...

对齐与非对齐访问
对齐与非对齐访问 什么是非对齐访问 在机器指令层面,当尝试从不能被 N 整除 (addr % N ! 0) 的起始地址读取 N 字节的数据时即发生了非对齐内存访问。举例而言,从地址 0x10004 读取 4 字节是可以的,然而从地址 0x10005 读取 4 字节数据将会…...
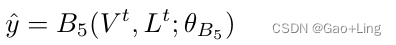
基于感知动作循环的层次推理用于视觉问答
title:Hierarchical Reasoning Based on Perception Action Cycle for Visual Question Answering 基于感知动作循环的层次推理用于视觉问答 文章目录title:[Hierarchical Reasoning Based on Perception Action Cycle for Visual Question Answering](…...

python中的.nc文件处理 | 05 NetCDF数据的进一步分析
NetCDF数据的进一步分析 比较不同数据集、不同季节的气候数据 import os import numpy as np import pandas as pd import matplotlib.pyplot as plt import cartopy.crs as ccrs import cartopy.feature as cfeature import seaborn as sns import geopandas as gpd import…...

GGX发布全新路线图,揭示具备 Layer0 特性且可编程的跨链基建生态
据彭博社报道,具备跨链通信且可编程的 Layer0 基础设施协议 Golden Gate (GGX) 已进行了 两年的线下开发,于近日公开发布了最新的路线图,该路线图不仅显示了该生态在过去两年的发展历程,也披露了 2023 年即将实现的重要里程碑。 G…...

taro+vue3 搭建一套框架,适用于微信小程序和H5
这里写tarovue3 搭建一套框架,适用于微信小程序和H5TaroVue3 搭建适用于微信小程序和 H5 的框架的大致步骤:TaroVue3 搭建适用于微信小程序和 H5 的框架的大致步骤: 安装 Taro。可以在终端输入以下命令进行安装: npm install -g…...

C++:模板初阶(泛型编程、函数模板、类模板)
文章目录1 泛型编程2 函数模板2.1 函数模板概念2.2 函数模板格式2.3 函数模板的原理2.4 函数模板的实例化2.5 模板参数的匹配原则3 类模板3.1 类模板的定义格式3.2 类模板的实例化1 泛型编程 所谓泛型,也就是通用型的意思。 在以往编写代码时,我们常常…...
)
把数组排成最小的数 AcWing(JAVA)
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。 例如输入数组 [3,32,321][3,32,321],则打印出这 33 个数字能排成的最小数字 321323321323。 数据范围 数组长度 [0,500][0,500]。 样例&#x…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
