当前位置：首页 > news >正文

【Python机器学习】实验04(2) 机器学习应用实践--手动调参

news 2026/5/28 20:10:28

文章目录

机器学习应用实践
- 1.1 准备数据
- - 此处进行的调整为：要所有数据进行拆分
- 1.2 定义假设函数
- - - Sigmoid 函数
- 1.3 定义代价函数
- 1.4 定义梯度下降算法
- - - gradient descent(梯度下降)
  - 此处进行的调整为：采用train_x, train_y进行训练
- 1.5 绘制决策边界
- 1.6 计算准确率
- - 此处进行的调整为：采用X_test和y_test来测试进行训练
- 1.7 试试用Sklearn来解决
- - 此处进行的调整为：采用X_train和y_train进行训练
  - 此处进行的调整为：采用X_test和y_test进行训练
- 1.8 如何选择超参数？比如多少轮迭代次数好？
- 1.9 如何选择超参数？比如学习率设置多少好？
- 1.10 如何选择超参数？试试调整l2正则化因子
- 实验4(2) 完成正则化因子的调参，下面给出了正则化因子lambda的范围，请参照学习率的调参，完成下面代码

机器学习应用实践

上一次练习中，我们采用逻辑回归并且应用到一个分类任务。

但是，我们用训练数据训练了模型，然后又用训练数据来测试模型，是否客观？接下来，我们仅对实验1的数据划分进行修改

需要改的地方为：下面红色部分给出了具体的修改。

1 训练数据数量将会变少

2 评估模型时要采用测试集

1.1 准备数据

本实验的数据包含两个变量(评分1和评分2，可以看作是特征),某大学的管理者，想通过申请学生两次测试的评分，来决定他们是否被录取。因此，构建一个可以基于两次测试评分来评估录取可能性的分类模型。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#利用pandas显示数据
path = 'ex2data1.txt'
data = pd.read_csv(path, header=None, names=['Exam1', 'Exam2', 'Admitted'])
data.head()

	Exam1	Exam2	Admitted
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

positive=data[data["Admitted"].isin([1])]
negative=data[data["Admitted"].isin([0])]

#准备训练数据
col_num=data.shape[1]
X=data.iloc[:,:col_num-1]
y=data.iloc[:,col_num-1]

X.insert(0,"ones",1)
X.shape

(100, 3)

X=X.values
X.shape

(100, 3)

y=y.values
y.shape

(100,)

此处进行的调整为：要所有数据进行拆分

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test =train_test_split(X,y,test_size=0.2,random_state=0)

train_x,test_x,train_y,test_y

(array([[ 1.        , 82.36875376, 40.61825516],[ 1.        , 56.2538175 , 39.26147251],[ 1.        , 60.18259939, 86.3085521 ],[ 1.        , 64.03932042, 78.03168802],[ 1.        , 62.22267576, 52.06099195],[ 1.        , 62.0730638 , 96.76882412],[ 1.        , 61.10666454, 96.51142588],[ 1.        , 74.775893  , 89.5298129 ],[ 1.        , 67.31925747, 66.58935318],[ 1.        , 47.26426911, 88.475865  ],[ 1.        , 75.39561147, 85.75993667],[ 1.        , 88.91389642, 69.8037889 ],[ 1.        , 94.09433113, 77.15910509],[ 1.        , 80.27957401, 92.11606081],[ 1.        , 99.27252693, 60.999031  ],[ 1.        , 93.1143888 , 38.80067034],[ 1.        , 70.66150955, 92.92713789],[ 1.        , 97.64563396, 68.86157272],[ 1.        , 30.05882245, 49.59297387],[ 1.        , 58.84095622, 75.85844831],[ 1.        , 30.28671077, 43.89499752],[ 1.        , 35.28611282, 47.02051395],[ 1.        , 94.44336777, 65.56892161],[ 1.        , 51.54772027, 46.85629026],[ 1.        , 79.03273605, 75.34437644],[ 1.        , 53.97105215, 89.20735014],[ 1.        , 67.94685548, 46.67857411],[ 1.        , 83.90239366, 56.30804622],[ 1.        , 74.78925296, 41.57341523],[ 1.        , 45.08327748, 56.31637178],[ 1.        , 90.44855097, 87.50879176],[ 1.        , 71.79646206, 78.45356225],[ 1.        , 34.62365962, 78.02469282],[ 1.        , 40.23689374, 71.16774802],[ 1.        , 61.83020602, 50.25610789],[ 1.        , 79.94481794, 74.16311935],[ 1.        , 75.01365839, 30.60326323],[ 1.        , 54.63510555, 52.21388588],[ 1.        , 34.21206098, 44.2095286 ],[ 1.        , 90.54671411, 43.39060181],[ 1.        , 95.86155507, 38.22527806],[ 1.        , 85.40451939, 57.05198398],[ 1.        , 40.45755098, 97.53518549],[ 1.        , 32.57720017, 95.59854761],[ 1.        , 82.22666158, 42.71987854],[ 1.        , 68.46852179, 85.5943071 ],[ 1.        , 52.10797973, 63.12762377],[ 1.        , 80.366756  , 90.9601479 ],[ 1.        , 39.53833914, 76.03681085],[ 1.        , 52.34800399, 60.76950526],[ 1.        , 76.97878373, 47.57596365],[ 1.        , 38.7858038 , 64.99568096],[ 1.        , 91.5649745 , 88.69629255],[ 1.        , 99.31500881, 68.77540947],[ 1.        , 55.34001756, 64.93193801],[ 1.        , 66.74671857, 60.99139403],[ 1.        , 67.37202755, 42.83843832],[ 1.        , 89.84580671, 45.35828361],[ 1.        , 72.34649423, 96.22759297],[ 1.        , 50.4581598 , 75.80985953],[ 1.        , 62.27101367, 69.95445795],[ 1.        , 64.17698887, 80.90806059],[ 1.        , 94.83450672, 45.6943068 ],[ 1.        , 77.19303493, 70.4582    ],[ 1.        , 34.18364003, 75.23772034],[ 1.        , 66.56089447, 41.09209808],[ 1.        , 74.24869137, 69.82457123],[ 1.        , 82.30705337, 76.4819633 ],[ 1.        , 78.63542435, 96.64742717],[ 1.        , 32.72283304, 43.30717306],[ 1.        , 75.47770201, 90.424539  ],[ 1.        , 33.91550011, 98.86943574],[ 1.        , 89.67677575, 65.79936593],[ 1.        , 57.23870632, 59.51428198],[ 1.        , 84.43281996, 43.53339331],[ 1.        , 42.26170081, 87.10385094],[ 1.        , 49.07256322, 51.88321182],[ 1.        , 44.66826172, 66.45008615],[ 1.        , 97.77159928, 86.72782233],[ 1.        , 51.04775177, 45.82270146]]),array([0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0,1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0,0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0,1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0], dtype=int64),array([[ 1.        , 80.19018075, 44.82162893],[ 1.        , 42.07545454, 78.844786  ],[ 1.        , 35.84740877, 72.90219803],[ 1.        , 49.58667722, 59.80895099],[ 1.        , 99.8278578 , 72.36925193],[ 1.        , 74.49269242, 84.84513685],[ 1.        , 69.07014406, 52.74046973],[ 1.        , 60.45788574, 73.0949981 ],[ 1.        , 50.28649612, 49.80453881],[ 1.        , 83.48916274, 48.3802858 ],[ 1.        , 34.52451385, 60.39634246],[ 1.        , 55.48216114, 35.57070347],[ 1.        , 60.45555629, 42.50840944],[ 1.        , 69.36458876, 97.71869196],[ 1.        , 75.02474557, 46.55401354],[ 1.        , 61.37928945, 72.80788731],[ 1.        , 50.53478829, 48.85581153],[ 1.        , 77.92409145, 68.97235999],[ 1.        , 52.04540477, 69.43286012],[ 1.        , 76.0987867 , 87.42056972]]),array([1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1],dtype=int64))

X_train.shape, X_test.shape, y_train.shape, y_test.shape

((80, 3), (20, 3), (80,), (20,))

train_x.shape,train_y.shape

((80, 3), (20, 3))

1.2 定义假设函数

Sigmoid 函数

$g$ 代表一个常用的逻辑函数（logistic function）为 $S$ 形函数（Sigmoid function），公式为： $g\left( z \right)=\frac{1}{1+{{e}^{-z}}}$
合起来，我们得到逻辑回归模型的假设函数：
${{h}}\left( x \right)=\frac{1}{1+{{e}^{-{{w }^{T}}x}}}$

def sigmoid(z):return 1 / (1 + np.exp(-z))

让我们做一个快速的检查，来确保它可以工作。

w=np.zeros((X.shape[1],1))

#定义假设函数h(x)=1/(1+exp^(-w.Tx))
def h(X,w):z=X@wh=sigmoid(z)return h

1.3 定义代价函数

 y_hat=sigmoid(X@w)

X.shape,y.shape,np.log(y_hat).shape

((100, 3), (100,), (100, 1))

现在，我们需要编写代价函数来评估结果。
代价函数：
$J\left(w\right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{({{y}^{(i)}}\log \left( {h}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h}\left( {{x}^{(i)}} \right) \right))}$

#代价函数构造
def cost(X,w,y):#当X(m,n+1),y(m,),w(n+1,1)y_hat=h(X,w)right=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())cost=-np.sum(right)/X.shape[0]return cost

#设置初始的权值
w=np.zeros((X.shape[1],1))
#查看初始的代价
cost(X,w,y)

0.6931471805599453

看起来不错，接下来，我们需要一个函数来计算我们的训练数据、标签和一些参数 $w$ 的梯度。

1.4 定义梯度下降算法

gradient descent(梯度下降)

这是批量梯度下降（batch gradient descent）
转化为向量化计算： $\frac{1}{m} X^T( Sigmoid(XW) - y )$
$\frac{\partial J\left( w \right)}{\partial {{w }_{j}}}=\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}}\left( {{x}^{(i)}} \right)-{{y}^{(i)}})x_{_{j}}^{(i)}}$

h(X,w).shape

(100, 1)

def grandient(X,y,iter_num,alpha):y=y.reshape((X.shape[0],1))w=np.zeros((X.shape[1],1))cost_lst=[]for i in range(iter_num):y_pred=h(X,w)-ytemp=np.zeros((X.shape[1],1))for j in range(X.shape[1]):right=np.multiply(y_pred.ravel(),X[:,j])gradient=1/(X.shape[0])*(np.sum(right))temp[j,0]=w[j,0]-alpha*gradientw=tempcost_lst.append(cost(X,w,y.ravel()))return w,cost_lst

此处进行的调整为：采用train_x, train_y进行训练

train_x.shape,train_y.shape

((80, 3), (20, 3))

iter_num,alpha=100000,0.001
w,cost_lst=grandient(X_train, y_train,iter_num,alpha)

cost_lst[iter_num-1]

0.38273008292061245

plt.plot(range(iter_num),cost_lst,"b-o")

[<matplotlib.lines.Line2D at 0x1d0f1417d30>]

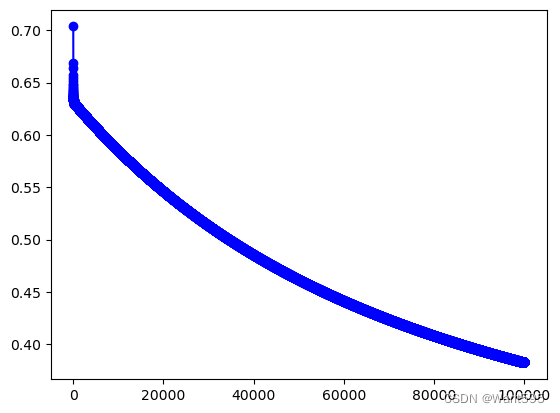
Xw—X(m,n) w (n,1)

array([[-4.86722837],[ 0.04073083],[ 0.04257751]])

1.5 绘制决策边界

高维数据的决策边界无法可视化

1.6 计算准确率

此处进行的调整为：采用X_test和y_test来测试进行训练

如何用我们所学的参数w来为数据集X输出预测，来给我们的分类器的训练精度打分。
逻辑回归模型的假设函数：
${{h}}\left( x \right)=\frac{1}{1+{{e}^{-{{w }^{T}}X}}}$
当 ${{h}}$ 大于等于0.5时，预测 y=1

当 ${{h}}$ 小于0.5时，预测 y=0 。

#在训练集上的准确率
y_train_true=np.array([1 if item>0.5 else 0 for item in h(X_train,w).ravel()])
y_train_true

array([1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0,1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1,1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0,1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0])

#训练集上的误差
np.sum(y_train_true==y_train)/X_train.shape[0]

0.9125

#在测试集上的准确率
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w).ravel()])
y_p_true

array([1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1])

y_test

array([1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1],dtype=int64)

np.sum(y_p_true==y_test)/X_test.shape[0]

0.95

1.7 试试用Sklearn来解决

此处进行的调整为：采用X_train和y_train进行训练

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression()
clf.fit(X_train,y_train)

LogisticRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

LogisticRegression

LogisticRegression()

#在训练集上的准确率为
clf.score(X_train,y_train)

0.9125

此处进行的调整为：采用X_test和y_test进行训练

#在测试集上却只有0.8
clf.score(X_test,y_test)

0.8

1.8 如何选择超参数？比如多少轮迭代次数好？

#1 利用pandas显示数据
path = 'ex2data1.txt'
data = pd.read_csv(path, header=None, names=['Exam1', 'Exam2', 'Admitted'])
data.head()

	Exam1	Exam2	Admitted
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

positive=data[data["Admitted"].isin([1])]
negative=data[data["Admitted"].isin([0])]
col_num=data.shape[1]
X=data.iloc[:,:col_num-1]
y=data.iloc[:,col_num-1]
X.insert(0,"ones",1)
X=X.values
y=y.values

# 1 划分数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.2, random_state=1)

X_train.shape,X_test.shape,X_val.shape

((64, 3), (20, 3), (16, 3))

y_train.shape,y_test.shape,y_val.shape

((64,), (20,), (16,))

# 2 修改梯度下降算法，为了不改变原有函数的签名，将训练集传给X,y
def grandient(X,y,X_val,y_val,iter_num,alpha):y=y.reshape((X.shape[0],1))w=np.zeros((X.shape[1],1))cost_lst=[]cost_val=[]lst_w=[]for i in range(iter_num):y_pred=h(X,w)-ytemp=np.zeros((X.shape[1],1))for j in range(X.shape[1]):right=np.multiply(y_pred.ravel(),X[:,j])gradient=1/(X.shape[0])*(np.sum(right))temp[j,0]=w[j,0]-alpha*gradientw=tempcost_lst.append(cost(X,w,y.ravel()))cost_val.append(cost(X_val,w,y_val.ravel()))lst_w.append(w)return lst_w,cost_lst,cost_val

#调用梯度下降算法
iter_num,alpha=6000000,0.001
lst_w,cost_lst,cost_val=grandient(X_train,y_train,X_val,y_val,iter_num,alpha)

plt.plot(range(iter_num),cost_lst,"b-+")
plt.plot(range(iter_num),cost_val,"r-^")
plt.legend(["train","validate"])
plt.show()

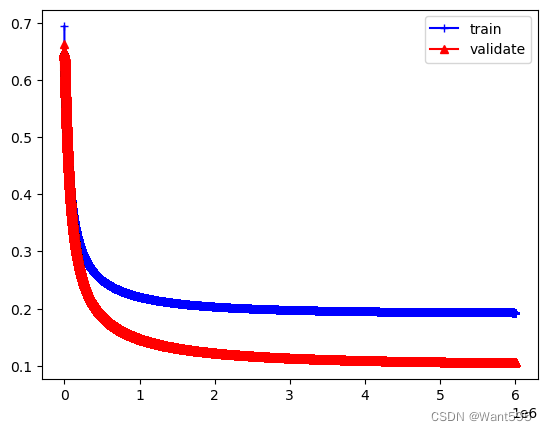
#分析结果,看看在300万轮时的情况
print(cost_lst[500000],cost_val[500000])

0.24994786329203897 0.18926411883434127

#看看5万轮时测试误差
k=50000
w=lst_w[k]
print(cost_lst[k],cost_val[k])
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w).ravel()])
y_p_true
np.sum(y_p_true==y_test)/X_test.shape[0]

0.45636730725628694 0.45732791872411350.7

#看看8万轮时测试误差
k=80000
w=lst_w[k]
print(cost_lst[k],cost_val[k])
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w).ravel()])
y_p_true
np.sum(y_p_true==y_test)/X_test.shape[0]

0.40603054170171965 0.394247838217765160.75

#看看10万轮时测试误差
k=100000
print(cost_lst[k],cost_val[k])
w=lst_w[k]
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w).ravel()])
y_p_true
np.sum(y_p_true==y_test)/X_test.shape[0]

0.381898564816469 0.363559834652638970.8

#分析结果,看看在300万轮时的情况
k=3000000
print(cost_lst[k],cost_val[k])
w=lst_w[k]
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w).ravel()])
y_p_true
np.sum(y_p_true==y_test)/X_test.shape[0]

0.19780791870188535 0.114326801305738750.85

#分析结果,看看在500万轮时的情况
k=5000000
print(cost_lst[k],cost_val[k])
w=lst_w[k]
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w).ravel()])
y_p_true
np.sum(y_p_true==y_test)/X_test.shape[0]

0.19393055410160026 0.107541811991899470.85

#在500轮时的情况
k=5999999print(cost_lst[k],cost_val[k])
w=lst_w[k]
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w).ravel()])
y_p_true
np.sum(y_p_true==y_test)/X_test.shape[0]

0.19319692059853838 0.106027626172624680.85

1.9 如何选择超参数？比如学习率设置多少好？

#1 设置一组学习率的初始值，然后绘制出在每个点初的验证误差，选择具有最小验证误差的学习率
alpha_lst=[0.1,0.08,0.03,0.01,0.008,0.003,0.001,0.0008,0.0003,0.00001]

def grandient(X,y,iter_num,alpha):y=y.reshape((X.shape[0],1))w=np.zeros((X.shape[1],1))cost_lst=[]for i in range(iter_num):y_pred=h(X,w)-ytemp=np.zeros((X.shape[1],1))for j in range(X.shape[1]):right=np.multiply(y_pred.ravel(),X[:,j])gradient=1/(X.shape[0])*(np.sum(right))temp[j,0]=w[j,0]-alpha*gradientw=tempcost_lst.append(cost(X,w,y.ravel()))return w,cost_lst


lst_val=[]
iter_num=100000
lst_w=[]
for alpha in alpha_lst:w,cost_lst=grandient(X_train,y_train,iter_num,alpha)lst_w.append(w)lst_val.append(cost(X_val,w,y_val.ravel()))
lst_val

C:\Users\sanly\AppData\Local\Temp\ipykernel_8444\2221512341.py:5: RuntimeWarning: divide by zero encountered in logright=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())
C:\Users\sanly\AppData\Local\Temp\ipykernel_8444\2221512341.py:5: RuntimeWarning: invalid value encountered in multiplyright=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())[nan,nan,nan,1.302365681883988,0.9807991089640924,0.6863333276415668,0.3635612014705094,0.3942497801600069,0.5169328809489743,0.6448319202310255]

np.array(lst_val)

array([       nan,        nan,        nan, 1.30236568, 0.98079911,0.68633333, 0.3635612 , 0.39424978, 0.51693288, 0.64483192])

lst_val[3:]

[1.302365681883988,0.9807991089640924,0.6863333276415668,0.3635612014705094,0.3942497801600069,0.5169328809489743,0.6448319202310255]

np.argmin(np.array(lst_val[3:]))

#最好的学习率为
alpha_best=alpha_lst[3+np.argmin(np.array(lst_val[3:]))]
alpha_best

0.001

#可视化各学习率对应的验证误差
plt.scatter(alpha_lst[3:],lst_val[3:])

<matplotlib.collections.PathCollection at 0x1d1d48738b0>

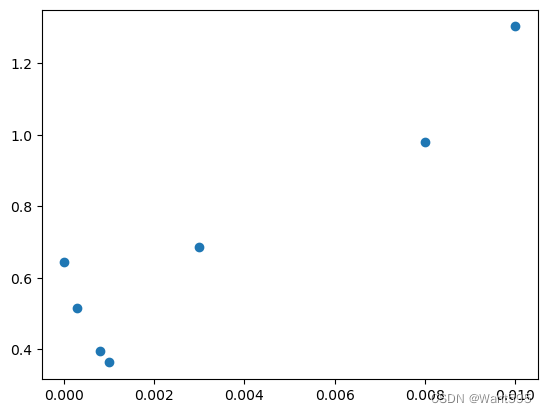
#看看测试集的结果
#取出最好学习率对应的w
w_best=lst_w[3+np.argmin(np.array(lst_val[3:]))]
print(w_best)
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w_best).ravel()])
y_p_true
np.sum(y_p_true==y_test)/X_test.shape[0]

[[-4.72412058][ 0.0504264 ][ 0.0332232 ]]0.8

#查看其他学习率对应的测试集准确率
for w in lst_w[3:]:y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w).ravel()])print(np.sum(y_p_true==y_test)/X_test.shape[0])

0.75
0.75
0.6
0.8
0.75
0.6
0.55

1.10 如何选择超参数？试试调整l2正则化因子

实验4(2) 完成正则化因子的调参，下面给出了正则化因子lambda的范围，请参照学习率的调参，完成下面代码

# 1正则化的因子的范围可以比学习率略微设置的大一些
lambda_lst=[0.001,0.003,0.008,0.01,0.03,0.08,0.1,0.3,0.8,1,3,10]

# 2 代价函数构造
def cost_reg(X,w,y,lambd):#当X(m,n+1),y(m,),w(n+1,1)y_hat=sigmoid(X@w)right1=np.multiply(y.ravel(),np.log(y_hat).ravel())+np.multiply((1-y).ravel(),np.log(1-y_hat).ravel())right2=(lambd/(2*X.shape[0]))*np.sum(np.power(w[1:,0],2))cost=-np.sum(right1)/X.shape[0]+right2return cost

def grandient_reg(X,w,y,iter_num,alpha,lambd):y=y.reshape((X.shape[0],1))w=np.zeros((X.shape[1],1))cost_lst=[] for i in range(iter_num):y_pred=h(X,w)-ytemp=np.zeros((X.shape[1],1))for j in range(0,X.shape[1]):if j==0:right_0=np.multiply(y_pred.ravel(),X[:,j])gradient_0=1/(X.shape[0])*(np.sum(right_0))temp[j,0]=w[j,0]-alpha*(gradient_0)else:right=np.multiply(y_pred.ravel(),X[:,j])reg=(lambd/X.shape[0])*w[j,0]gradient=1/(X.shape[0])*(np.sum(right))temp[j,0]=w[j,0]-alpha*(gradient+reg)          w=tempcost_lst.append(cost_reg(X,w,y,lambd))return w,cost_lst

# 3 调用梯度下降算法用l2正则化
iter_num,alpha=100000,0.001
cost_val=[]
cost_w=[]
for lambd in lambda_lst:w,cost_lst=grandient_reg(X_train,w,y_train,iter_num,alpha,lambd)cost_w.append(w)cost_val.append(cost_reg(X_val,w,y_val,lambd))

cost_val

[0.36356132605416125,0.36356157522133403,0.3635621981384864,0.36356244730503007,0.36356493896065706,0.3635711680214138,0.36357365961439897,0.3635985745598491,0.3636608540941533,0.36368576277656284,0.36393475122711266,0.36480480418120226]

# 4 查找具有最小验证误差的索引，从而求解出最优的lambda值
idex=np.argmin(np.array(cost_val))
print("具有最小验证误差的索引为{}".format(idex))
lamba_best=lambda_lst[idex]
lamba_best

具有最小验证误差的索引为00.001

# 5 计算最好的lambda对应的测试结果
w_best=cost_w[idex]
print(w_best)
y_p_true=np.array([1 if item>0.5 else 0 for item in h(X_test,w_best).ravel()])
y_p_true
np.sum(y_p_true==y_test)/X_test.shape[0]

[[-4.7241201 ][ 0.05042639][ 0.0332232 ]]0.8

【Python机器学习】实验04(2) 机器学习应用实践--手动调参

文章目录机器学习应用实践1.1 准备数据此处进行的调整为：要所有数据进行拆分 1.2 定义假设函数Sigmoid 函数 1.3 定义代价函数1.4 定义梯度下降算法gradient descent(梯度下降) 此处进行的调整为：采用train_x, train_y进行训练 1.5 绘制决策边界1.6 计算…...

编程日记 2023/7/29 9:57:36

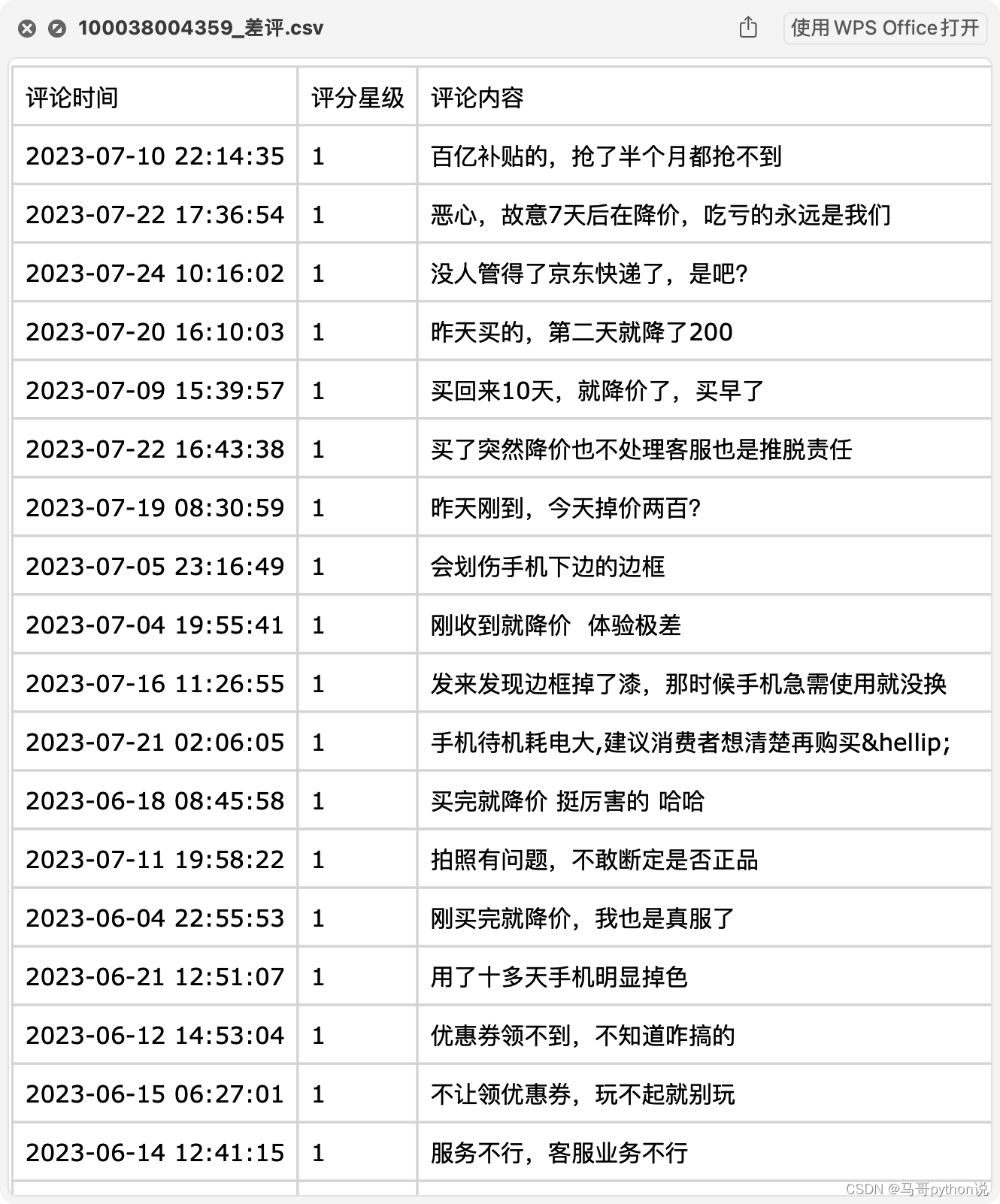
【爬虫案例】用Python爬取iPhone14的电商平台评论

用python爬取某电商网站的iPhone14评论数据， 爬取目标： 核心代码如下： 爬取到的5分好评： 爬取到的3分中评： 爬取到的1分差评： 所以说，用python开发爬虫真的很方面！ 您好&…...

编程日记 2023/7/29 9:56:34

01)docker学习 centos7离线安装docker

docker学习 centos7离线安装docker 在实操前可以先看下docker教程，https://www.runoob.com/docker/docker-tutorial.html ，不过教程上都是在线安装方式，很方便，离线安装肯定比如在线麻烦点。一、什么是Docker 在学习docker时，在网上看到一篇博文讲得很好，自己总结一下…...

编程日记 2023/7/29 9:55:33

前端 - 实习两个星期总结

文章目录吐槽总结新人建议项目学习到的今天已经是菜鸟实习的第二个星期了，怎么说呢，反正就是进的一个不大不小的厂，做着不难不易的事，菜鸟现在主要做的就是适配！现在就来总结一下，不过这之前，…...

编程日记 2023/7/29 9:54:32

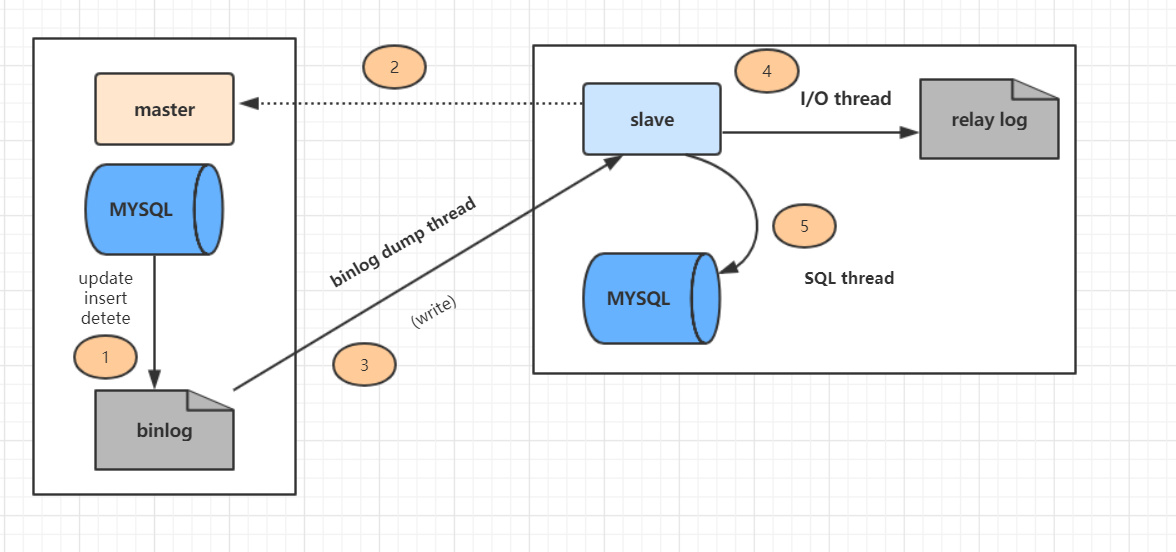
MySQL——主从复制

1.理解MySQL主从复制原理。 2.完成MySQL主从复制。 1.理解MySQL主从复制原理。 1）、MySQL支持的复制类型 （1）、基于语句（ statement ）的复制在主服务器上执行SQL 语句，在从服务器上执行同样的语句。 My…...

编程日记 2023/7/29 9:53:31

报表下载工具

1.需求说明我有一堆文件的Url地址， 现在需要按照企业，项目和报表类型分类下载到对应的文件夹中 2.相关实体类企业文件夹定义 package com.vz.utils.report;import lombok.Data; import java.util.ArrayList; import java.util.List; import java.uti…...

编程日记 2023/7/29 9:52:29

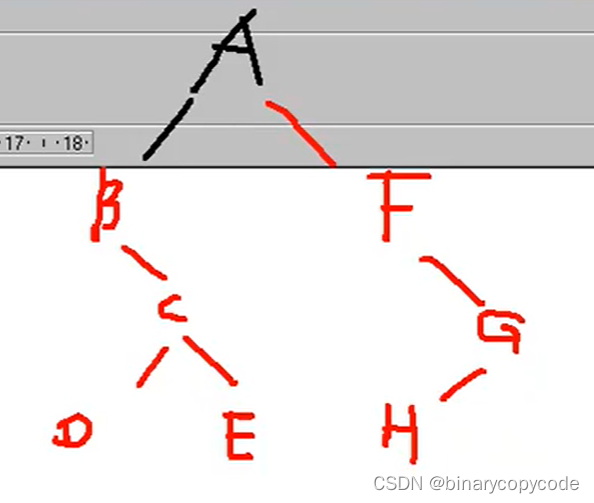
树及其遍历

文章目录树树定义专业术语树分类二叉树分类存储连续存储（完全二叉树）链式存储一般树的存储森林的存储线索二叉树哈夫曼树构造步骤遍历先序遍历中序遍历后续遍历链式二叉树遍历具体代码已知两种遍历序列求原始二叉树已知先序和中序求后序已知中序和后…...

编程日记 2023/7/29 9:51:27

Qt报错解决办法

anaconda环境安装qt报错解决办法报错：thresholdGap: 20 pointsShape: 164142 qt.qpa.plugin: Could not find the Qt platform plugin “wayland” in “/home/tianhailong/anaconda3/envs/edge_algorithm/lib/python3.8/site-packages/cv2/qt/plugins” This app…...

编程日记 2023/7/29 9:50:26

Python（四十七）列表对象的创建

❤️ 专栏简介：本专栏记录了我个人从零开始学习Python编程的过程。在这个专栏中，我将分享我在学习Python的过程中的学习笔记、学习路线以及各个知识点。 ☀️ 专栏适用人群 ：本专栏适用于希望学习Python编程的初学者和有一定编程基础的人。无…...

编程日记 2023/7/29 9:49:25

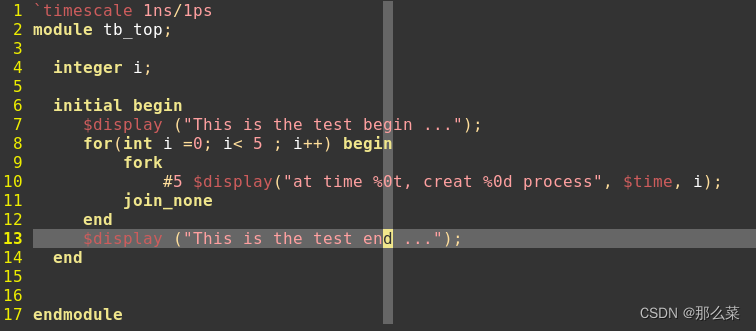
#systemverilog# 说说Systemverilog中《automatic》那些事儿

前面我们学习了有关systemverilog语言中有关《static》的一些知识，同static 关系比较好的哥们，那就是《automatic》。今天，我们了解认识一下。在systemveriog中，存在三种并发执行语句，分别是fork..join，fork...join_any和fork..join_none，其中只有fork...join_none不…...

编程日记 2023/7/29 9:48:24

C/C++ 动态内存分配与它的指针变量

一、什么是内存的动态分配全局变量分配在内存中的静态存储区。局部变量（包括形参）分配在内存中的动态存储区，这个存储区是一个称为栈的区域。除此之外，C语言还允许建立内存动态分配区域，以存放一些临时用的数据&…...

编程日记 2023/7/29 9:47:23

UE5初学者快速入门教程

虚幻引擎是一系列游戏开发工具，能够将 2D 手机游戏制作为 AAA 游戏机游戏。虚幻引擎 5 用于开发下一代游戏，包括Senuas Saga: Hellblade 2、Redfall（来自 Arkane Austin 的合作射击游戏）、Dragon Quest XII: The Flames of Fate、…...

编程日记 2023/7/29 9:46:19

论文笔记--FEDERATED LEARNING: STRATEGIES FOR IMPROVING COMMUNICATION EFFICIENCY

论文笔记--FEDERATED LEARNING: STRATEGIES FOR IMPROVING COMMUNICATION EFFICIENCY 1. 文章简介2. 文章概括3 文章重点技术3.1 联邦学习(federated learning, FL)3.2 Structured updates3.3 Sketched Update 4. 文章亮点5. 原文传送门 1. 文章简介标题：FEDERATE…...

编程日记 2023/7/29 9:45:18

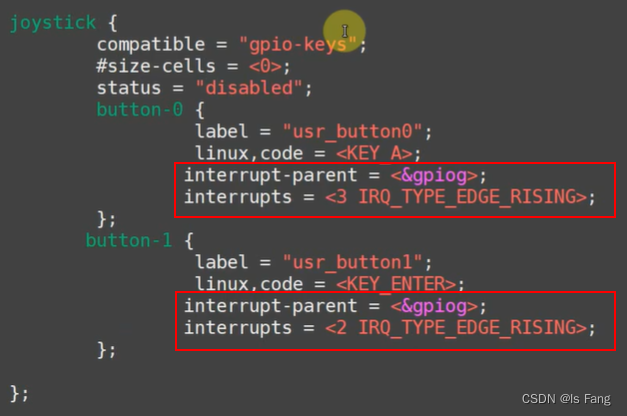
STM32MP157驱动开发——按键驱动（异步通知）

文章目录 “异步通知 ”机制：信号的宏定义：信号注册 APP执行过程驱动编程做的事应用编程做的事异步通知方式的按键驱动程序(stm32mp157)button_test.cgpio_key_drv.cMakefile修改设备树文件编译测试 “异步通知 ”机制： 信号的宏定义&#x…...

编程日记 2023/7/29 9:44:16

医疗器械维修工程师心得

彩虹医械维修技能班9月将开展本年第三期长期班，目前咨询人员也陆续多了起来，很多刚了解到医疗行业的，自身也没有多少相关的基础，在咨询时会问到没有基础能否学的会？ 做了这行业的都知道，无论多么复杂的设备…...

编程日记 2023/7/29 9:43:12

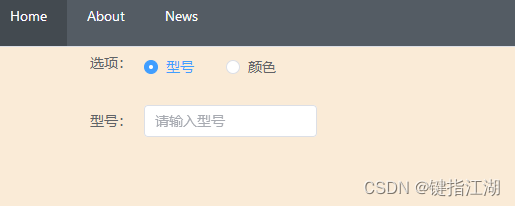
Vue3 Radio单选切换展示不同内容

Vue3 Radio单选框切换展示不同内容环境：vue3tsviteelement plus 技巧：v-if，v-show的使用实现功能：点击单选框展示不同的输入框效果实现前的代码： <template><div class"home"><el-row …...

编程日记 2023/7/29 9:42:11

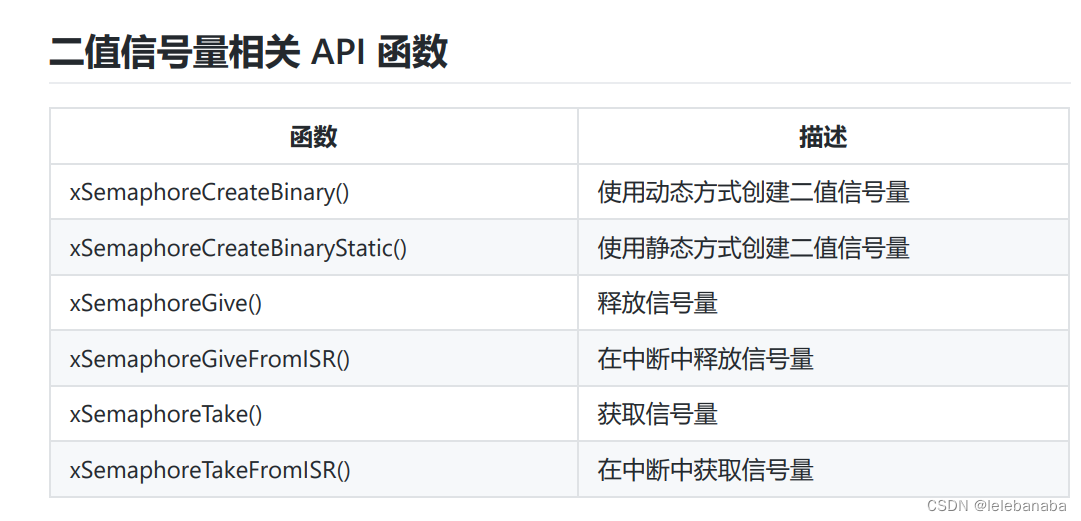
FreeRTOS之二值信号量

什么是信号量？ 信号量（Semaphore），是在多任务环境下使用的一种机制，是可以用来保证两个或多个关键代码段不被并发调用。信号量这个名字，我们可以把它拆分来看，信号可以起到通知信号的作用&am…...

编程日记 2023/7/29 9:41:09

ChatGPT API进阶调用指南

原文：ChatGPT API进阶调用指南 ChatGPT API 进阶调用指南 ChatGPT API 是基于 OpenAI 的 GPT模型的一个强大工具，可以用于构建各种对话式应用。以下是一些使用 Markdown 语法的进阶调用指南，以帮助您更好地利用 ChatGPT API。设置用户角色…...

编程日记 2023/7/29 9:40:08

人工智能术语翻译（四）

文章目录摘要MNOP 摘要人工智能术语翻译第四部分，包括I、J、K、L开头的词汇！ M 英文术语中文翻译常用缩写备注Machine Learning Model机器学习模型Machine Learning机器学习ML机器学习Machine Translation机器翻译MTMacro Average宏平均Macro-F1宏…...

编程日记 2023/7/29 9:39:07

kubernetes持久化存储卷

kubernetes持久化存储卷 kubernetes持久化存储卷一、存储卷介绍二、存储卷的分类三、存储卷的选择四、本地存储卷之emptyDir五、本地存储卷之 hostPath六、网络存储卷之nfs七、PV(持久存储卷)与PVC(持久存储卷声明)7.1 认识pv与pvc7.2 pv与pvc之间的关系7.3 实现nfs类型pv与pvc…...

编程日记 2023/7/29 9:38:06

Jetson Orin Nano 升级jetpack5.1.2刷机过程记录

一.刷机起因 orin nano 接了个IMX477的摄像头,用命令行DISPLAY:0.0 nvgstcapture-1.0 显示的画面有撕裂,让卖家查问题,卖家测试没有撕裂,对比环境,orin nano出厂默认的是jetpack5.1.1,卖家用的jetpack5.1.2版本,为了解决差异,要升级jetpack版本,前后搞了2天半,记录一下. 另外…...

编程新知 2026/5/26 4:48:24

T型翼/尾板导向的穿浪双体船姿态控制【附代码】

✨ 长期致力于穿浪双体船、T型翼、尾板、多自由度姿态控制、舒适性评估研究工作，擅长数据搜集与处理、建模仿真、程序编写、仿真设计。 ✅ 专业定制毕设、代码 ✅ 如需沟通交流，点击《获取方式》 （1）动态水翼升力模型与耦合运动方…...

编程新知 2026/5/26 4:32:22

告别沉浸式白屏！UniApp中iOS/Android底部安全区与顶部状态栏颜色自定义全攻略

告别沉浸式白屏！UniApp中iOS/Android底部安全区与顶部状态栏颜色自定义全攻略当开发者尝试在UniApp中实现沉浸式设计时，往往会遇到一个令人头疼的问题——默认的白色安全区和状态栏导致界面元素（如电池图标、信号强度）几乎不可见。…...

编程新知 2026/5/26 3:13:58

如何快速掌握开源UE资产编辑器：UAssetGUI完整配置与实战指南

如何快速掌握开源UE资产编辑器：UAssetGUI完整配置与实战指南【免费下载链接】UAssetGUI A tool designed for low-level examination and modification of Unreal Engine game assets by hand. 项目地址: https://gitcode.com/gh_mirrors/ua/UAssetGUI UAss…...

编程新知 2026/5/26 1:33:08

2605.VGGT-Omega 论文解读: 3D重建的Scaling Law, Register Attention效率革命 | Oxford+Meta CVPR26 Oral

VGGT-Omega: Scaling Feed-Forward 3D Reconstruction Jianyuan Wang, Minghao Chen, Shangzhan Zhang, Nikita Karaev, Johannes Schonberger, et al. Visual Geometry Group, Oxford Meta AI | CVPR 2026 Oral | arXiv 2605.15195 Paper | Project Page 一句话总结 VGGT-Om…...