一起学数据结构(1)——复杂度
目录
1. 时间复杂度:
1.1 时间复杂度的概念:
1.2 时间复杂度的表示及计算:
1.3 较为复杂的时间复杂度的计算:
2. 空间复杂度:
2.1 空间复杂度的概念:
2.2 空间复杂度的计算:
1. 时间复杂度:
1.1 时间复杂度的概念:
时间复杂度是一个函数,用于衡量一个算法的运行快慢,对于一个算法而言,在不同配置上的机器运行的速度是不一样的,所以,并不能简单的用运行的时间来衡量算法的运行快慢。虽然用时间来表示并不合理,但是,一个算法运行的时间与这个算法中基本操作的次数成正比,所以,将一个算法中的基本操作的运行次数定义为时间复杂度。
1.2 时间复杂度的表示及计算:
上面给出了时间复杂度的概念后,这里给出一个例子:
void Func1(int N)
{ int count = 0;for (int i = 0; i < N ; ++ i)
{for (int j = 0; j < N ; ++ j){++count;}
}for (int k = 0; k < 2 * N ; ++ k)
{++count;
}int M = 10;
while (M--)
{++count;
}
通过上面给出的定义可以知道,时间复杂度是一个关于算法中基本操作运行次数的函数,对上述代码,如果将它的运行次数用函数表示,即:
不过,实际中计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要知道执行的大概次数,并且取对结果有决定性因素的一样来表示。例如,对于上面的函数式,取决定性作用的一项是。在表示时,采用 大O的渐进表示法 ,对于上述代码,可以表示为O(N^2).
对于时间复杂的的计算,在不同的情况下有不同的规则,下面通过举例来引出这些规则:
例1:
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}
}
int M = 10;
while (M--){++count;}
printf("%d\n", count);
按照上面所说的方法,用函数来表示上述代码中基本操作的运行次数,即:
取函数中有决定性因素的项,即:,不过在用大O的渐进法进行表示时,在N的前面存在一个常数,需要满足用常数1取代运行时间中的所有加法常数这个规则,所以,时间复杂度表示为O(N).
例2:
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}
}for (int k = 0; k < N ; ++ k){++count;}
printf("%d\n", count);
此时的时间复杂度为:,因为不能分辨,M、N二者的大小,所以也就不能分辩二者谁在时间复杂度中起决定性作用。
如果给出的条件足以分别二者之间的大小关系:
当时,时间复杂度可以表示为:
当时,时间复杂度可以表示为:
当时,时间复杂度可以表示为;
或者
例3:
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
对于例3所给出的代码,执行次数为100次,并不是一个函数式,对于这种只有常数的类型,用来表示。
例4:
const char * strchr ( const char * str, int character );strchr函数的功能实在一个字符串中,寻找和某个目标字符相同的字符。假设,字符串的长度为N,查找的次数表示为K对于在这个字符串中查找目标字符,可以分为三种情况:
第一种情况: 第一次就找到目标字符,执行次数为1.
第二种情况:在时找到目标字符。
第三种情况: 最坏的情况,即时找到目标字符。
对于这种多情况的代码的时间复杂度,按照最坏的情况进行表示,所以,例4的时间复杂度为。
在了解了时间复杂度的基本运算规则即表示后,下面引入一些较为复杂的时间复杂度的计算:
1.3 较为复杂的时间复杂度的计算:
例1:
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end) {int exchange = 0;for (size_t i = 1; i < end; ++i){(a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}
if (exchange == 0)
break}
}对于例1,即冒泡排序的复杂度的计算:需要注意,当有循环嵌套时,时间复杂度的计算应按照累加,而不是累乘,对于冒泡排序,可以理解为,共有N中情况,每种情况中代码的基本操作的执行次数一次为,即满足一个等差数列。但是需要注意,冒泡排序的执行次数依旧有三种情况,假设代码的执行次数为K:
第一种情况:最好的情况,给定的数组有序。此时
第二种情况:
第三种情况:最坏的情况,此时
通过前面对时间复杂度的介绍,可以得出,冒泡排序的时间复杂度为:
例2:
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;
// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}
return -1;
对于二分查找的时间复杂度的计算: 假设,数据的总量为N,每次查找后,数据的总量会/2,也就是说,查找K次后的数据总量为,对于二分查找而言,最坏的情况就是查找K次后,
此时,K和N的关系可以表示为 (注:此时的log以2为底)。由于文本编辑的原因,以2为底的对数不容易编写,所以,将以2为底的对数写成
,对非2为底的对数不成立!
例3:
long long Fac(size_t N)
{if(0 == N)return 1;
}return Fac(N-1)*N;
}
对于递归算法,其时间复杂度是多次调用的代码的次数的累加,所以,对于例3给出的递归,调用的次数最大是次,所以,时间复杂度是
。
如果,对于例3中的代码做一点简单的修改,即:
long long Fac(size_t N)
{if(0 == N)return 1;
}for( size_t i = 0; i < N; i++){.......}return Fac(N-1)*N;
}与例3不同的是,在例3中的最后一行代码表达的意思就是递归运算后的结果×,时间复杂度
只与递归的调用次数有关,对于递归后面×的N,只是对结果进行乘法。
但是,在这个例子中,递归的次数一共是次,但是,在每次递归的时候,中间会有一个
循环,所以,代码一共会递归
次,但是,每次在递归中,循环的次数是
次,前面说到对于递归算法的时间复杂度,是多次调用的代码的次数的累加,并不是类乘,因此,对于次代码整体的逻辑可以理解为一个等差数列,时间复杂度为
例4:
long long Fib(size_t N)
{if(N < 3)return 1;
}return Fib(N-1) + Fib(N-2);
}
例4是一个双动递归,对于这种递归的时间复杂度的运算,由下面的一张图来表示:
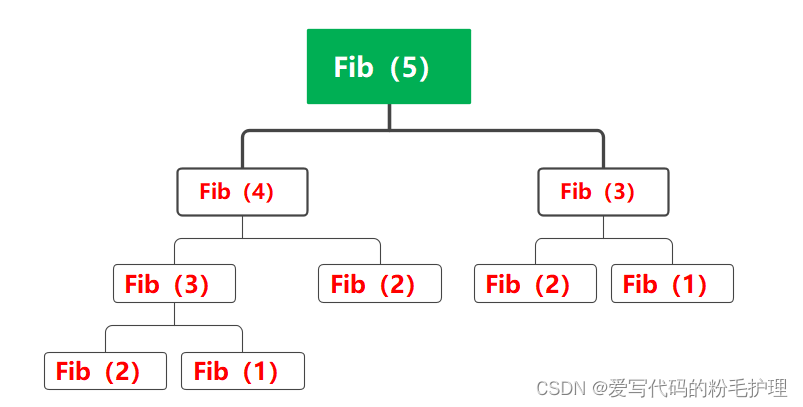
如图所示是参数为5时的调用情况。如果,当参数为时,调用情况会变成下图所示:
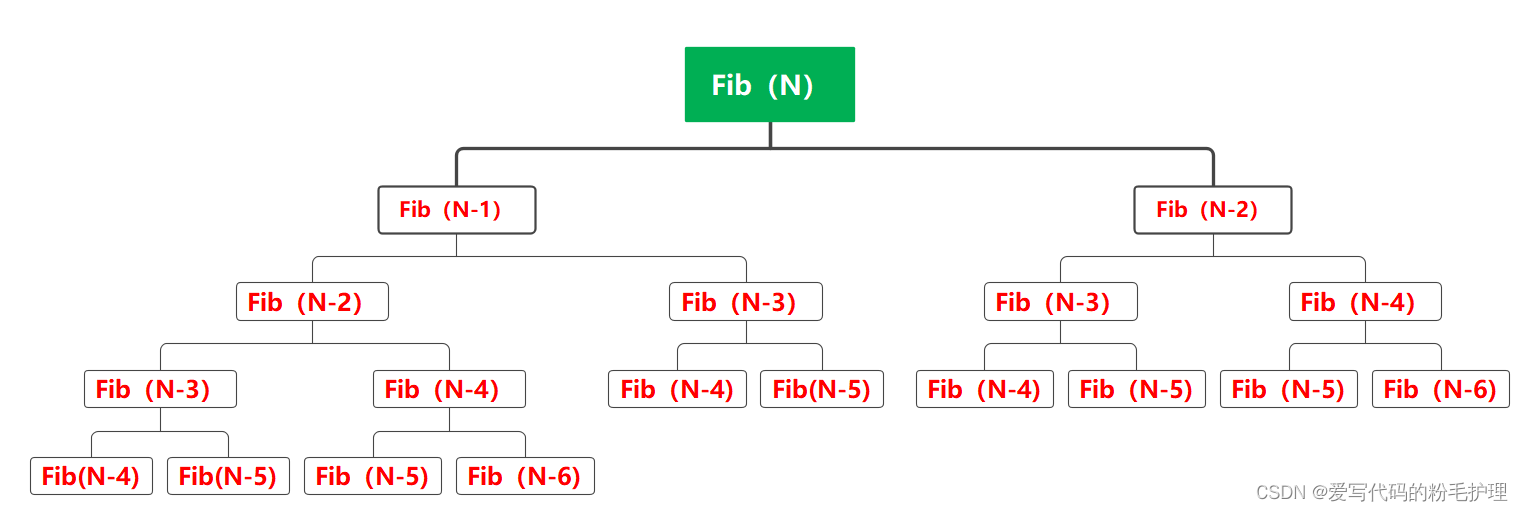
稍加观察会发现,图中每一行的项的个数都满足的数量。再结合上面的图像不难得出一个结论,如果按照图中的计算方法一直进行下去,右边数据到达
的速度大于左边,所以,当所有的项都变成
时,图形的结构可以用下面的图片表示:
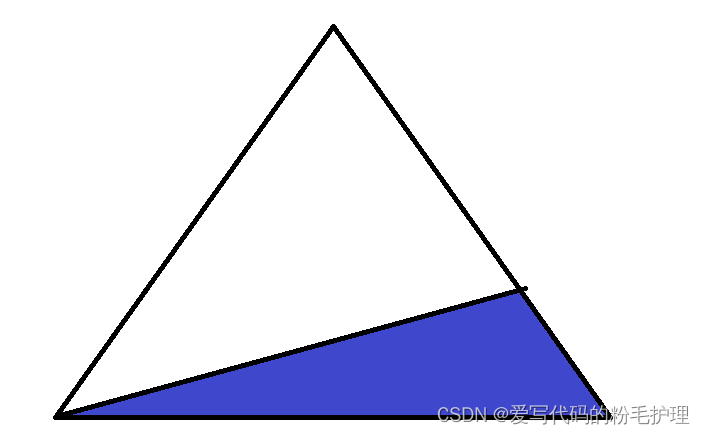
其中白色和蓝色的交界处表示此时递归变成了 。蓝色部分表示下面没有项,所以,当蓝色部分出现后,每一行的元素数量不再严格的满足
.但是,当
很大是,即使缺少了一部分,此时所有项之和的数量级,依旧和
类似,在此处也可以理解为,三角形项的和的极限无限趋近于
。 所以,对于上面给出的递归,其时间复杂度为
2. 空间复杂度:
2.1 空间复杂度的概念:
在介绍时间复杂度的概念时说过,时间复杂度是一个函数表达式,同样,对于空间复杂度来说也是一个函数表达式 ,对算法运行过程中临时占用存储空间大小的量度。但是对于空间复杂度,并不是指程序占用了多少bytes的空间,空间复杂度针对的目标是变量的个数。
2.2 空间复杂度的计算:
对于空间复杂度的计算,依旧通过给出例子来计算不同情况下的空间复杂度:
例1:
void BubbleSort(int* a, int n){assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}}
还是拿冒泡排序举例,在计算时间复杂度时,最后得出冒泡排序的时间复杂度是。
对于冒泡排序时间复杂度的计算,通过上面给出的概念,可以知道,时间复杂度针对的对象是代码中临时占用内存空间的变量,可以理解为,为了解决某个问题或者为了完成代码而创建的变量,对于上面的代码,可以看出,为了完成冒泡排序,创建了三个变量分别是。所以,上述代码中临时占用内存空间的变量的数量为3,所以,冒泡排序的空间复杂度为
。
例2:
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}
return fibArray;
例2中,为了完成代码,所以,利用动态内存函数malloc创建了个临时占用空间的变量。下面虽然也创建了变量i,但是,空间复杂度仍然是取起决定性作用的值,所以,例2的空间复杂度为
。
例3:
long long Fac(size_t N){{if(N == 0)return 1;}return Fac(N-1)*N;}
对于递归而言,每次运算都要开辟常数量的空间,需要开辟次,所以,空间复杂度为
。
例4:
long long Fib(int N)
{{ if(N < 3)return 1;}return Fib(N-1) + Fib(N-2);
}
在计算双动递归的空间复杂度之前,需要了解一个概念,及:时间是累加的,空间是可以重复利用的。对于这句话和求双动递归的空间复杂度有什么关系,可以用计算双动递归的时间复杂度的图来解释:

图反应的只是双动递归执行的大体结构,但是,不反应双动递归运行时的顺序,对于双动递归运行时的顺序,是。当
运行后,加上
所占用的空间,可以看成一共占用了5个内存空间。返回
,此时
所占用的内存空间还给操作系统,下次执行时,再执行
,但是对于
的使用,并不会再开辟一个新的内存空间,而是将
还给操作系统的空间再给
使用,这也就对应了上面的话:空间是可以重复利用的。对于其他元素,同样出现重复利用内存空间的情况。所以,计算双动递归的空间复杂度时,计算的应该是递归一直向下执行时(即不出现上面所说的重复利用空间的情况)所占用内存的最大值,所以,对于
,向下执行时所占用内存空间的最大值为
。因此,双动递归的空间复杂度为
。
相关文章:
一起学数据结构(1)——复杂度
目录 1. 时间复杂度: 1.1 时间复杂度的概念: 1.2 时间复杂度的表示及计算: 1.3 较为复杂的时间复杂度的计算: 2. 空间复杂度: 2.1 空间复杂度的概念: 2.2 空间复杂度的计算: 1. 时间复杂度…...
<el-date-picker>组件选择开始时间,结束时间自动延长30min
背景:选择开始时间,结束时间自动增加30分钟,结束时间也可重新选择,如图: <el-form-item label"预约开始时间" prop"value1"><el-date-pickersize"large"v-model"ruleForm…...

eslint-webpack-plugin
说明:现在eslint已经弃用了eslint-loader,如果要安装来使用的话,会报错,烦死人 大概的报错信息如下: ERROR in ./src/index.js Module build failed (from ./node_modules/eslint-loader/dist/cjs.js): TypeError: Cannot read …...

logback中文一直是乱码,logback中文问号
logback一直是乱码 方案一加上UTF-8 方案二我这边方案一不行 在启动参数加上 -Dfile.encodingutf-8 这个竟然就可以了...
C++之文件操作
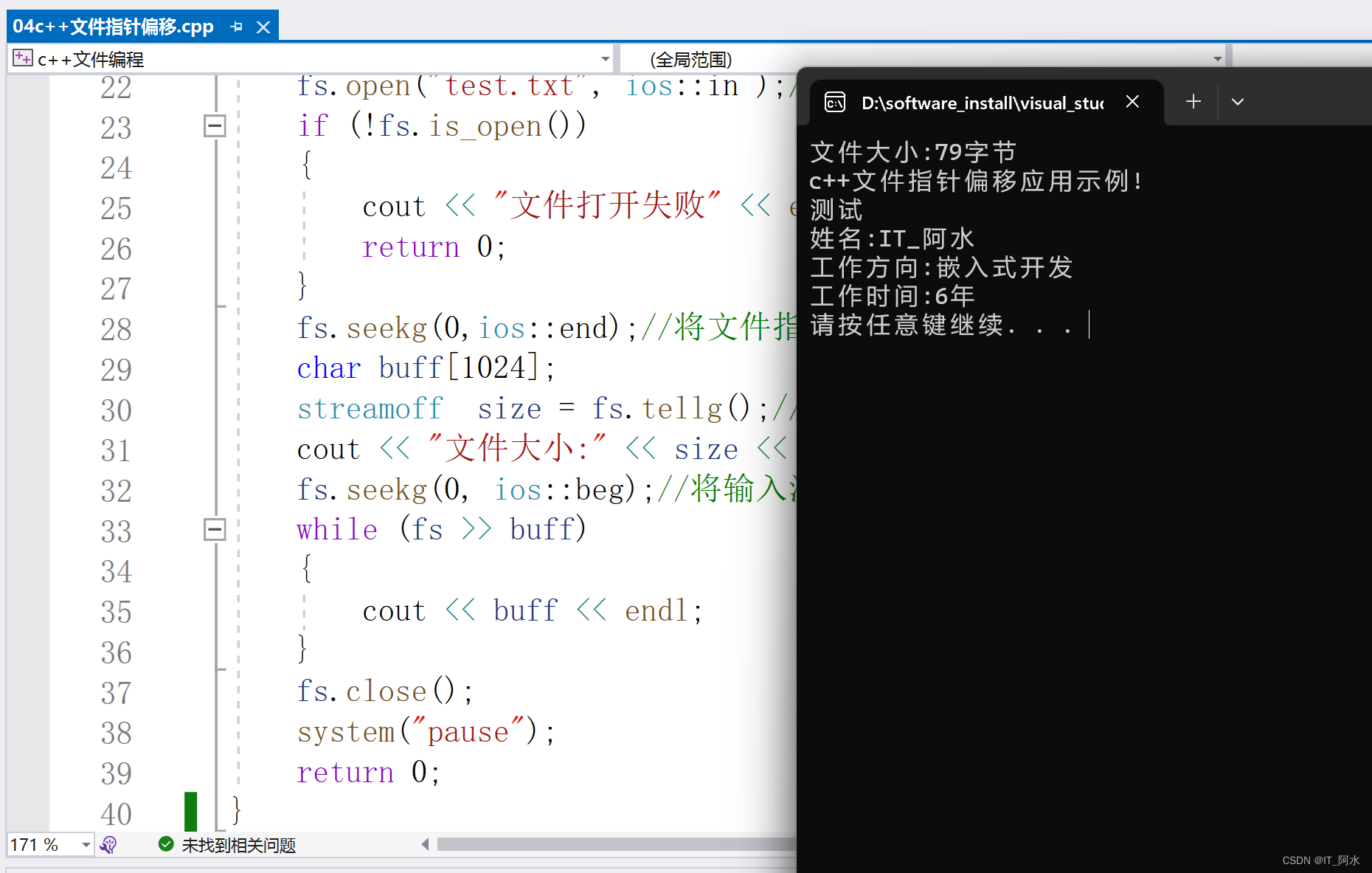
1.C文件操作 C中文件操作头文件:fstream。 文件类型:文件文件和二进制文件。 文件操作三大类: ofstream 写操作 ifstream 读操作 fstream:读写操作 文件打开方式: 标志说明ios::in只读ios::out只写,文件不存在则…...

CentOS 7.6安装 MongoDB 5.0.2
https://developer.aliyun.com/article/983777 我遇到的问题:如何以集群的方式启动,使用replSet的方式进行启动: 需要在配置文件上加上replSet的信息 port27017 #端口 bind_ip0.0.0.0 #默认是127.0.0.1 dbpath/usr/local/mongodb/data #数据…...
Windows下安装python3教程
参考:https://blog.csdn.net/kailingr/article/details/128193083 一、安装步骤图解 准备工作: 进官网https://www.python.org/下载Python 安装包,注意:Python 3.9不能在Windows 7或更早版本上使用 安装: 1.下载完之后双击该文…...
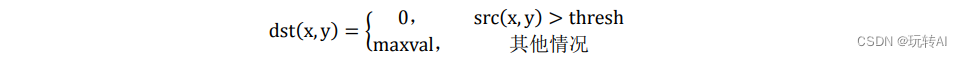
opencv-27 阈值处理 cv2.threshold()
怎么理解阈值处理? 阈值处理(Thresholding)是一种常用的图像处理技术,在机器学习和计算机视觉中经常被用于二值化图像或二分类任务。它基于设定一个阈值来将像素值进行分类,将像素值大于或小于阈值的部分分为两个不同的类别&…...
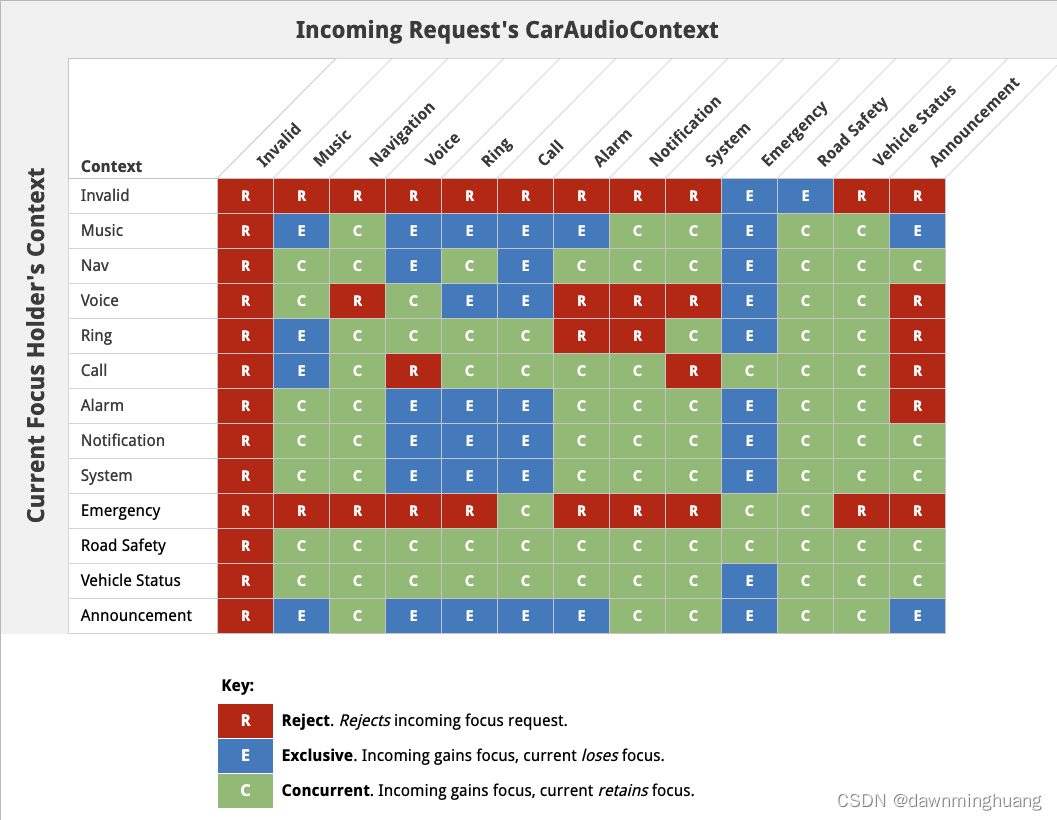
AAOS 音频焦点请求
文章目录 前言基本概念提供给应用来获取音频焦点的apiAAOS中的音频焦点管理交互矩阵duck的实现流程AAOS 测试应用kitchensink焦点相关 前言 本文章的目标是首先了解Android中音频焦点的基本概念,理解代码中相关音频焦点的使用方法。其次理解AAOS 中相关交互矩阵概念…...

订单系统中的幂等实现
一.订单提交的例子 一个订单生成并支付的过程,大致为:用户点击前端页面提交订单->后端根据此次提交信息生成订单->用户确认订单并进行支付操作->支付成功。 主要分为前端层面,后端系统层面,数据库层面。前端层面不详述…...
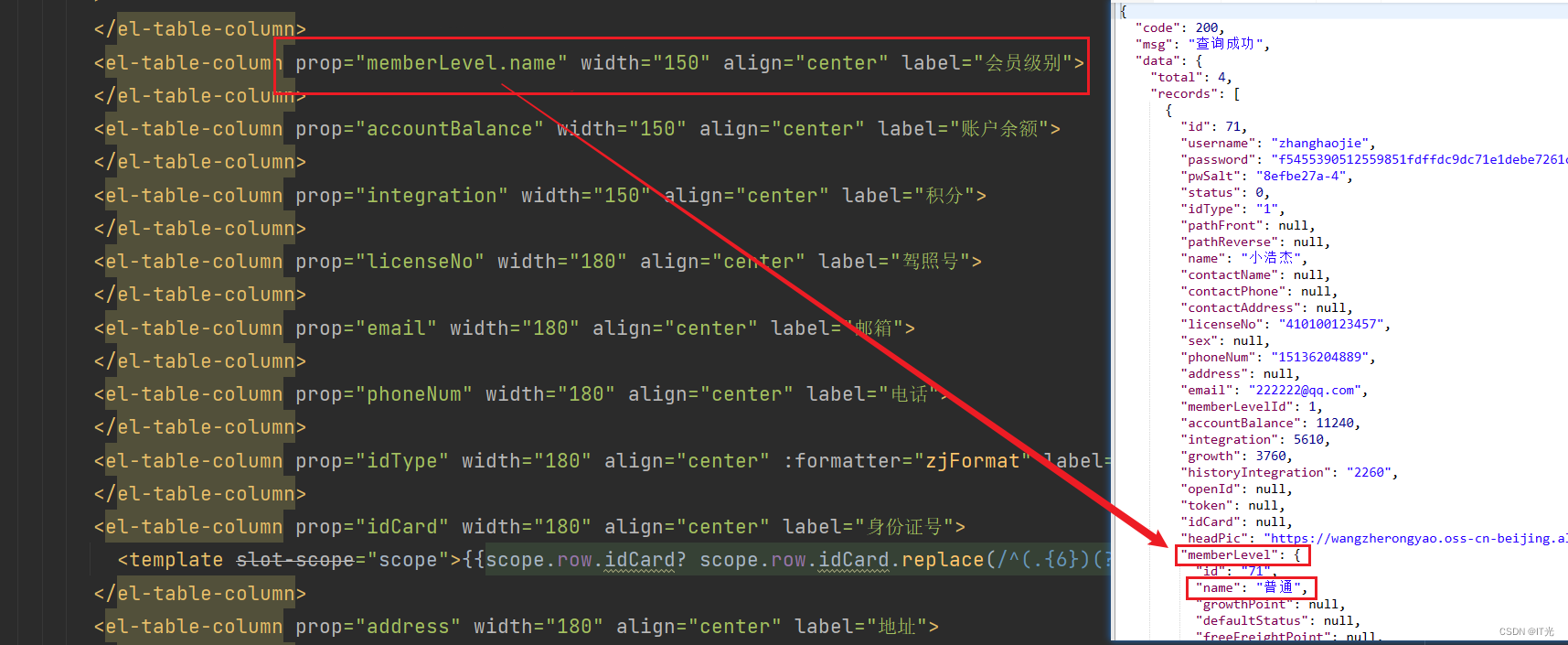
三个常用查询:根据用户名 / token查询用户信息+链表分页条件查询
目录 1.根据用户名或者token查询用户信息 会员信息实体类 统一状态Result类 controller层 service层及实现类 dao层 测试: 2.链表分页条件查询 会员等级实体类 封装条件类PageVo controller层 service层及实现类 dao层 Mapper.xml层 测试 vue前端参考 1.根据用户名…...

列表、张量、向量和矩阵的关系
在数学和编程中,列表、张量、向量和矩阵之间有一定的关系。这些概念在不同领域和语境中有略微不同的定义和用法,以下是它们之间的一般关系: 列表(List): 列表是编程语言中的一种数据结构,用于存…...
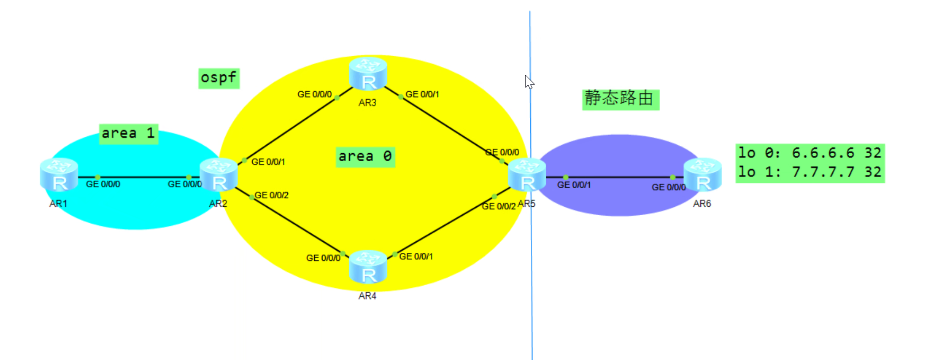
华为数通HCIP-ISIS高级
isis区域间的互访 1、L2区域 to L1区域 在L1区域发布的路由会以L1-LSP在L1区域内传递,到达L1-2路由器时,L1-2路由器会将该L1-LSP转换为L2-LSP在L2区域内传递; 因此L2区域的设备可以学习到L1区域的明细路由,进行访问;…...
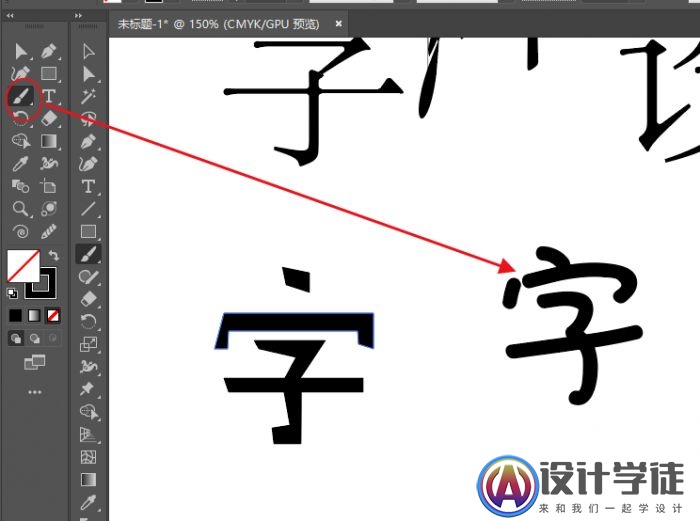
CorelDraw怎么做立体字效果?CorelDraw制作漂亮的3d立体字教程
1、打开软件CorelDRAW 2019,用文本工具写上我们所需要的大标题。建议字体选用比较粗的适合做标题的字体。 2、给字填充颜色,此时填充的颜色就是以后立体字正面的颜色。我填充了红色,并加上了灰色的描边。 3、选中文本,单击界面左侧…...
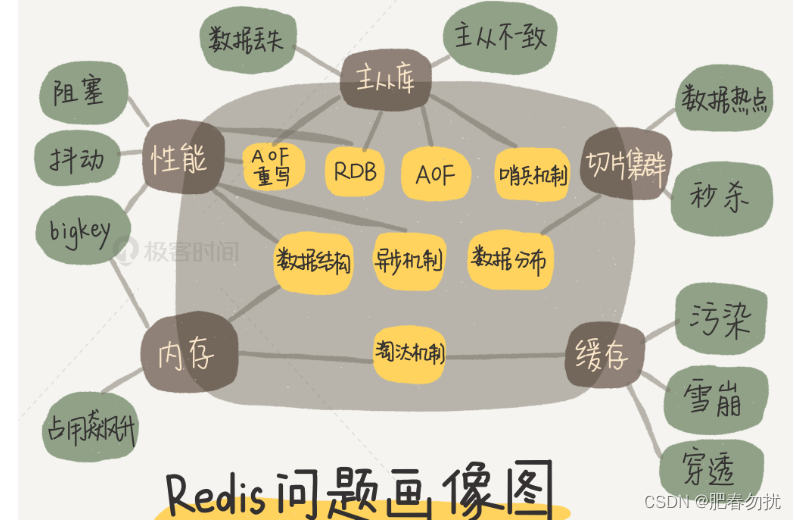
大致了解Redis
为了保证数据的可靠性,Redis 需要在磁盘上读写 AOF 和 RDB,但在高并发场景里,这就会直接带来两个新问题:一个是写 AOF 和RDB 会造成 Redis 性能抖动,另一个是 Redis 集群数据同步和实例恢复时,读 RDB 比较慢…...

javaweb会话技术
cookie的入门使用 package com.hspedu.cookie;import javax.servlet.ServletException; import javax.servlet.http.Cookie; import javax.servlet.http.HttpServlet; import javax.servlet.http.HttpServletRequest; import javax.servlet.http.HttpServletResponse; import …...
android app控制ros机器人三(android登录界面)
接下来是二次开发的具体环节了,由于存在用户需求,用到ros-mobile不多,更偏向于android开发。 用ppt画了简单的展示界面,与用后交流界面的功能布局。先开发一代简易版本的app,后续可以丰富完善。ctrlcv上线。 登录界面…...
Android版本的发展4-13
Android 4.4 KitKat 1、通过主机卡模拟实现新的 NFC 功能。 2、低功耗传感器,传感器批处理,步测器和计步器。 3、全屏沉浸模式,隐藏所有系统 UI,例如状态栏和导航栏。它适用于鲜艳的视觉内容,例如照片、视频、地图、…...

【2023.7.29】浅谈手办——新人入坑指南
目录 前言入坑指南1.声明2.介绍3.树状图 总结参考文章 前言 出于对动漫的热爱,相信很多人都会买手办,本人在大一时开始入手了第一个手办,超大猿王路飞(高约50cm),当时对手办还不是很了解,只知道…...
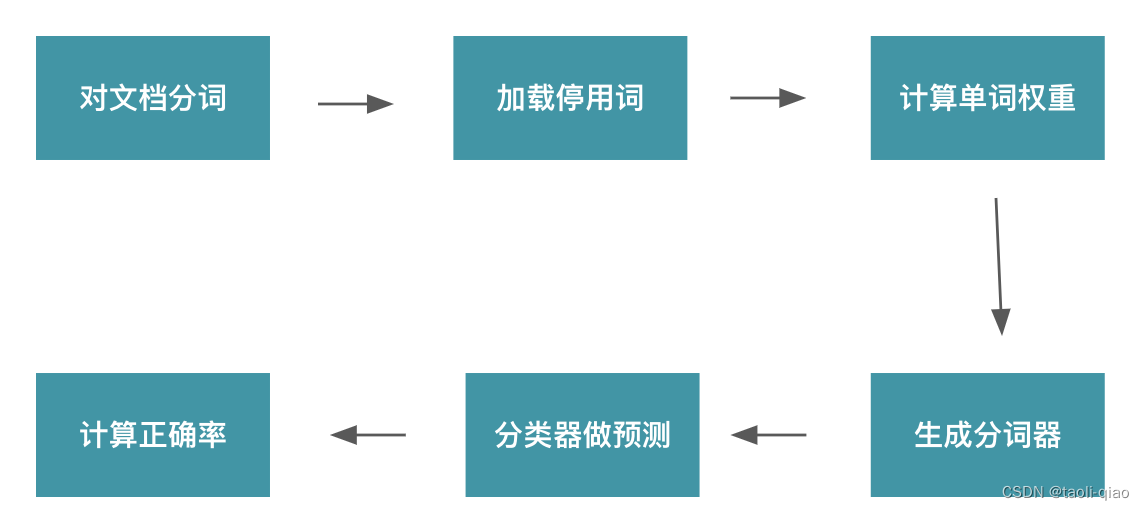
使用贝叶斯算法完成文档分类问题
贝叶斯原理 贝叶斯原理(Bayes theorem)是一种用于计算条件概率的数学公式。它是以18世纪英国数学家托马斯贝叶斯(Thomas Bayes)的名字命名的。贝叶斯原理表达了在已知某个事件发生的情况下,另一个事件发生的概率。具体…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
