列表、张量、向量和矩阵的关系
在数学和编程中,列表、张量、向量和矩阵之间有一定的关系。这些概念在不同领域和语境中有略微不同的定义和用法,以下是它们之间的一般关系:
-
列表(List):
列表是编程语言中的一种数据结构,用于存储多个元素。列表中的元素可以是任意数据类型,包括数字、字符串、布尔值等。在Python中,列表用方括号[]表示。列表是一维的,也就是说它只有一个维度。 -
张量(Tensor):
张量是多维数组(或多维矩阵)的一般化。它是深度学习框架(如PyTorch和TensorFlow)中最基本的数据结构。张量可以是零维(标量)、一维(向量)、二维(矩阵)或更高维。在机器学习和深度学习中,张量通常用于表示数据和模型的参数。 -
向量(Vector):
向量是一种特殊的张量,它是一维的数组。向量通常用于表示方向和大小,其中每个元素表示在某个方向上的数值。在数学中,向量可以表示为行向量或列向量。在深度学习中,向量通常用于表示样本的特征或模型的参数。 -
矩阵(Matrix):
矩阵是一种特殊的张量,它是二维的数组。矩阵通常用于表示线性映射或多个向量的组合。在数学中,矩阵由行和列组成,通常表示为大写字母。在深度学习中,矩阵通常用于表示权重矩阵、卷积核等。
在深度学习中,通常使用张量来表示数据和模型的参数,其中:
- 零维张量就是标量,即一个单独的数值。
- 一维张量就是向量,表示为一串数值。
- 二维张量就是矩阵,表示为一个二维数组。
- 更高维度的张量可以看作是多个矩阵堆叠而成的。
在深度学习中,对于数据的处理和计算都是基于张量来进行的,因此张量是非常重要的概念。向量和矩阵是张量的一种特殊形式,它们在深度学习中具有重要的应用和意义。
相关文章:

列表、张量、向量和矩阵的关系
在数学和编程中,列表、张量、向量和矩阵之间有一定的关系。这些概念在不同领域和语境中有略微不同的定义和用法,以下是它们之间的一般关系: 列表(List): 列表是编程语言中的一种数据结构,用于存…...
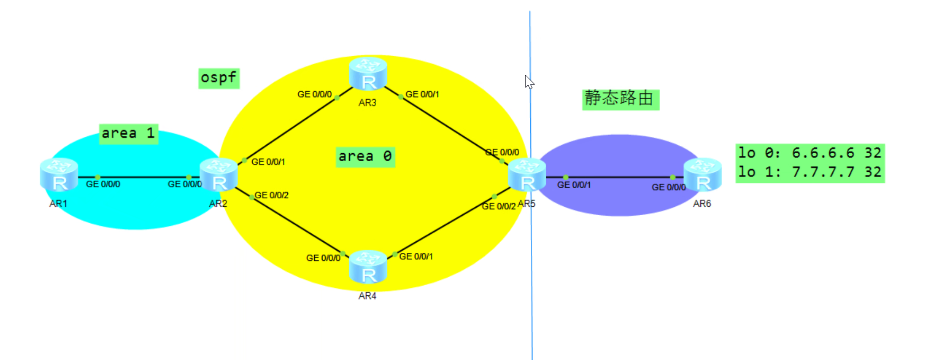
华为数通HCIP-ISIS高级
isis区域间的互访 1、L2区域 to L1区域 在L1区域发布的路由会以L1-LSP在L1区域内传递,到达L1-2路由器时,L1-2路由器会将该L1-LSP转换为L2-LSP在L2区域内传递; 因此L2区域的设备可以学习到L1区域的明细路由,进行访问;…...
CorelDraw怎么做立体字效果?CorelDraw制作漂亮的3d立体字教程
1、打开软件CorelDRAW 2019,用文本工具写上我们所需要的大标题。建议字体选用比较粗的适合做标题的字体。 2、给字填充颜色,此时填充的颜色就是以后立体字正面的颜色。我填充了红色,并加上了灰色的描边。 3、选中文本,单击界面左侧…...
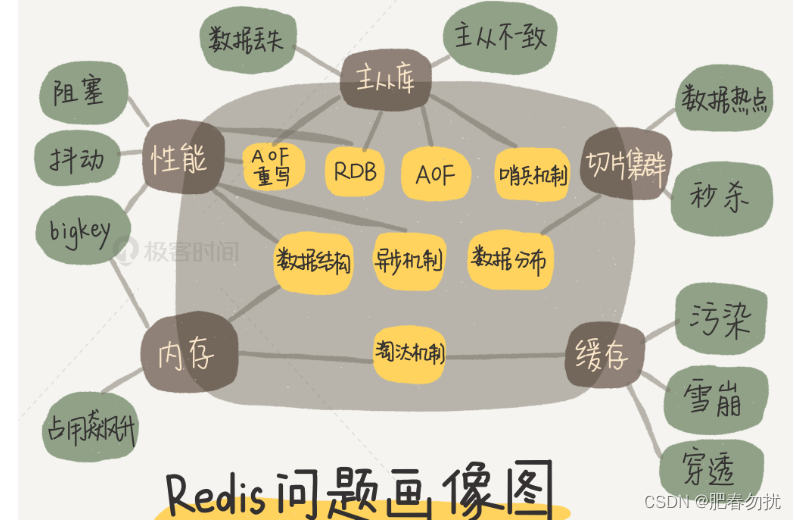
大致了解Redis
为了保证数据的可靠性,Redis 需要在磁盘上读写 AOF 和 RDB,但在高并发场景里,这就会直接带来两个新问题:一个是写 AOF 和RDB 会造成 Redis 性能抖动,另一个是 Redis 集群数据同步和实例恢复时,读 RDB 比较慢…...

javaweb会话技术
cookie的入门使用 package com.hspedu.cookie;import javax.servlet.ServletException; import javax.servlet.http.Cookie; import javax.servlet.http.HttpServlet; import javax.servlet.http.HttpServletRequest; import javax.servlet.http.HttpServletResponse; import …...
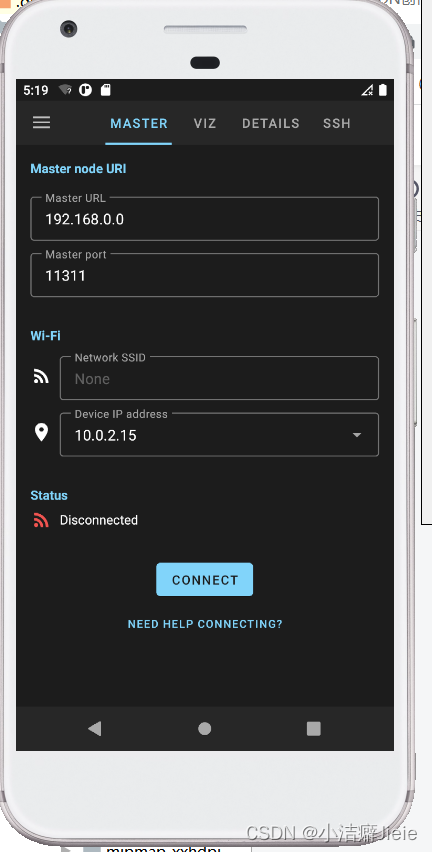
android app控制ros机器人三(android登录界面)
接下来是二次开发的具体环节了,由于存在用户需求,用到ros-mobile不多,更偏向于android开发。 用ppt画了简单的展示界面,与用后交流界面的功能布局。先开发一代简易版本的app,后续可以丰富完善。ctrlcv上线。 登录界面…...
Android版本的发展4-13
Android 4.4 KitKat 1、通过主机卡模拟实现新的 NFC 功能。 2、低功耗传感器,传感器批处理,步测器和计步器。 3、全屏沉浸模式,隐藏所有系统 UI,例如状态栏和导航栏。它适用于鲜艳的视觉内容,例如照片、视频、地图、…...

【2023.7.29】浅谈手办——新人入坑指南
目录 前言入坑指南1.声明2.介绍3.树状图 总结参考文章 前言 出于对动漫的热爱,相信很多人都会买手办,本人在大一时开始入手了第一个手办,超大猿王路飞(高约50cm),当时对手办还不是很了解,只知道…...
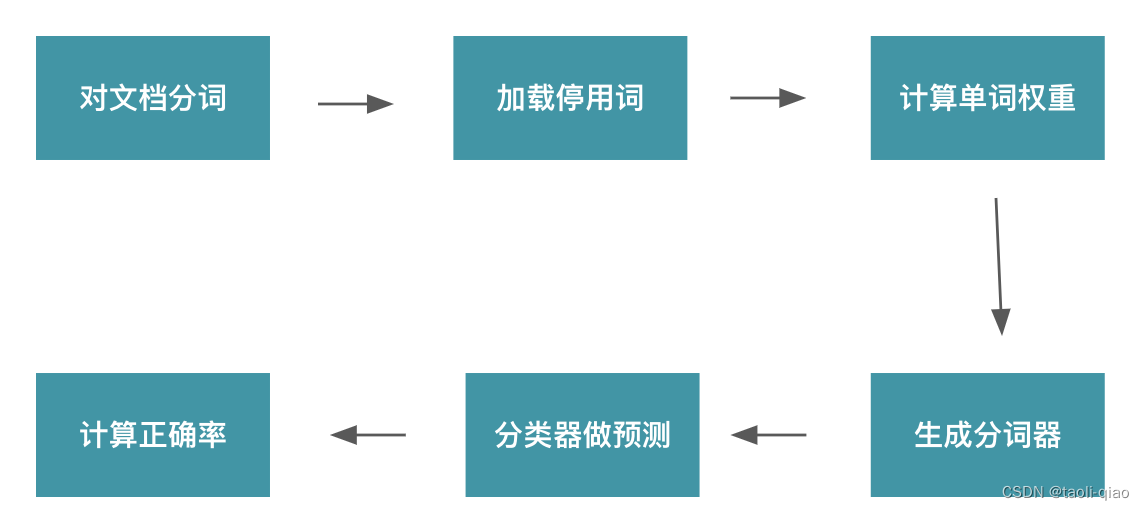
使用贝叶斯算法完成文档分类问题
贝叶斯原理 贝叶斯原理(Bayes theorem)是一种用于计算条件概率的数学公式。它是以18世纪英国数学家托马斯贝叶斯(Thomas Bayes)的名字命名的。贝叶斯原理表达了在已知某个事件发生的情况下,另一个事件发生的概率。具体…...

【Kafka】消息队列Kafka进阶
目录 Kafka分区机制生产者分区写入策略轮询策略随机策略(不用)按key分配策略乱序问题自定义分区策略 消费者组Rebalance机制消费者分区分配策略Range范围分配策略RoundRobin轮询策略Stricky粘性分配策略 Kafka副本机制producer的ACKs参数acks配置为0acks…...

学习day55
消息订阅与发布 消息订阅与发布是一种组件间通信的方式,适用于任意组件间通信 使用步骤: 安装pubsub:npm i pubsub-js 引入:import pubsub from pubsub-js 接收数据:A组件想接收数据,则在A组件中订阅消息…...

C++-Rust-一次性掌握两门语言
C-Rust-一次性掌握两门语言 简介特色数据类型声明常量、变量判断与循环函数抽象化的对象:类与接口枚举模板与泛型Lambda匿名函数表达式 简介 本文主要是通过介绍C和Rust的基础语法达成极速入门两门开发语言。 C是在C语言的基础之上添加了面向对象的类、重载、模板等…...

汇编调用C语言定义的全局变量
在threadx移植中,系统的systick通过了宏定义的方式定义,很难对接库函数的时钟频率,不太利于进行维护 所以在C文件中自己定义了一个systick_Div的变量,通过宏定义方式设定systick的时钟频率 在汇编下要加载这个systick分频系数 …...

WEB 文件包含 /伪协议
首先谈谈什么是文件包含 WEB入门——文件包含漏洞与PHP伪协议_文件包含php伪协议_HasntStartIsOver的博客-CSDN博客 文件包含 程序员在编写的时候 可能写了自己的 函数 如果想多次调用 那么就需要 重新写在源代码中 太过于麻烦了只需要写入 funcation.php然后在需要引用的地…...
)
ComPDFKit PDF SDK库(支持Windows、Web、Android、iOS、Mac等平台)
ComPDFKit提供专业、全平台支持的PDF开发库,包括Windows、Mac、Linux、Android、iOS、Web平台。开发者可以快速、灵活整合PDF功能到各开发平台的软件、程序、系统中。丰富的功能,多种开发语言,灵活的部署方案可供选择,满足您对PDF…...

微服务契约测试框架-Pact
契约测试 契约测试的思想就是将原本的 Consumer 与 Provider 间同步的集成测试,通过契约进行解耦,变成 Consumer 与 Provider 端两个各自独立的、异步的单元测试。 契约测试的优点: 契约测试与单元测试以及其它测试之间没有重复,…...
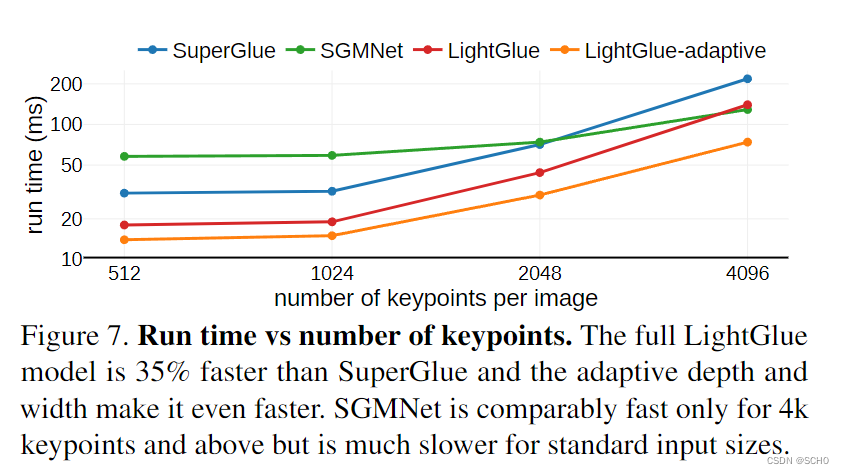
LightGlue论文翻译
LightGlue:光速下的局部特征匹配 摘要 - 我们介绍 LightGlue,一个深度神经网络,学习匹配图像中的局部特征。我们重新审视 SuperGlue 的多重设计决策,稀疏匹配的最新技术,并得出简单而有效的改进。累积起来,它们使 Lig…...

iOS开发-CAShapeLayer与UIBezierPath实现微信首页的下拉菜单效果
iOS开发-CAShapeLayer与UIBezierPath实现微信首页的下拉菜单效果 之前开发中遇到需要使用实现微信首页的下拉菜单效果。用到了CAShapeLayer与UIBezierPath绘制菜单外框。 一、效果图 二、CAShapeLayer与UIBezierPath 2.1、CAShapeLayer是什么? CAShapeLayer继承自…...

《Elasticsearch 源码解析与优化实战》第5章:选主流程
《Elasticsearch 源码解析与优化实战》第5章:选主流程 - 墨天轮 一、简介 Discovery 模块负责发现集群中的节点,以及选择主节点。ES 支持多种不同 Discovery 类型选择,内置的实现称为Zen Discovery ,其他的包括公有云平台亚马逊的EC2、谷歌…...

Spring Cloud Alibaba - Nacos源码分析(三)
目录 一、Nacos客户端服务订阅的事件机制 1、监听事件的注册 2、ServiceInfo处理 serviceInfoHolder.processServiceInfo 一、Nacos客户端服务订阅的事件机制 Nacos客户端订阅的核心流程:Nacos客户端通过一个定时任务,每6秒从注册中心获取实例列表&…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
