[nlp] tokenizer加速:fast_tokenizer=True
fast_tokenizer 是一个布尔值参数,用于指定是否使用快速的 tokenizer。在某些情况下,使用快速的 tokenizer 可以加快模型训练和推理速度。如果 fast_tokenizer 参数为 True,则会使用快速的 tokenizer;否则,将使用默认的 tokenizer。
快速的 tokenizer 通常使用一些技巧来减少 tokenization 过程中的计算量,以便更快地处理文本数据。其中一种常见的技巧是使用字典或哈希表来存储单词,而不是使用字符串。这样可以避免在字符串中搜索和替换子字符串的操作,从而提高 tokenization 的速度。
另外,快速的 tokenizer 还可以使用一些预处理技术,例如将单词转换为其基本形式(即去掉后缀或前缀),或者将多个连续的空格或标点符号合并为一个空格或标点符号。
总之,快速的 tokenizer 通过使用一些优化技巧和预处理技术来减少计算量,从而提高 tokenization 的速度。
tokenizer = load_hf_tokenizer(args.model_name_or_path_baseline, fast_tokenizer=True)def load_hf_tokenizer(model_name_or_path, fast_tokenizer=True):if os.path.exists(model_name_or_path):# Locally tokenizer loading has some issue, so we need to forc相关文章:

[nlp] tokenizer加速:fast_tokenizer=True
fast_tokenizer 是一个布尔值参数,用于指定是否使用快速的 tokenizer。在某些情况下,使用快速的 tokenizer 可以加快模型训练和推理速度。如果 fast_tokenizer 参数为 True,则会使用快速的 tokenizer;否则,将使用默认的 tokenizer。 快速的 tokenizer 通常使用一些技巧来减…...
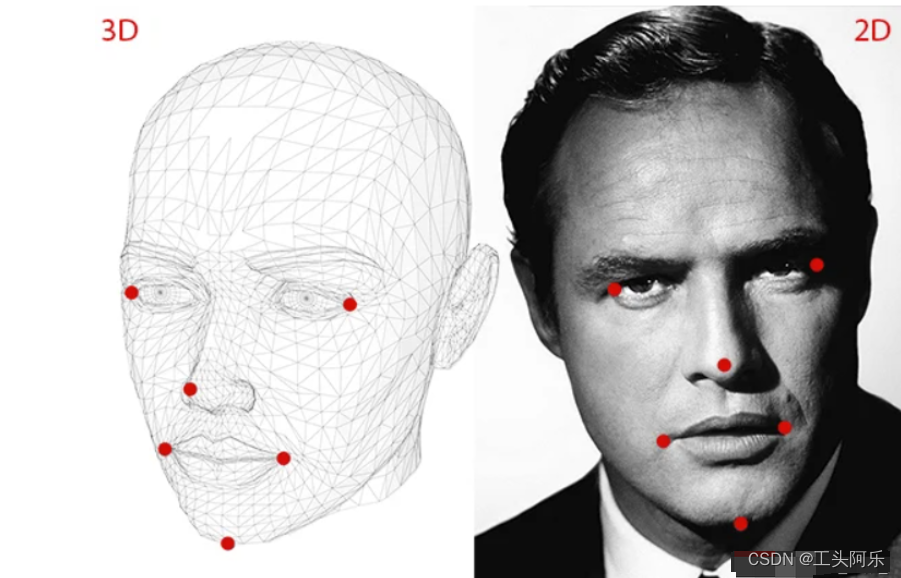
基于OpenCV solvePnP函数估计头部姿势
人脸识别 文章目录 人脸识别一、姿势估计概述1、概述2、姿态估计3、在数学上表示相机运动4、姿势估计需要什么5、姿势估计算法6、Levenberg-Marquardt 优化 二、solvePnP函数1、函数原型2、参数详解 三、OpenCV源码1、源码路径 四、效果图像示例参考链接 一、姿势估计概述 1、…...

STC12C5A系列单片机内部 EEPROM 的应用
参考范例程序。 eeprom.c #include "eeprom.h"/*---------------------------- Disable ISP/IAP/EEPROM function Make MCU in a safe state ----------------------------*/ void IapIdle() {IAP_CONTR 0; //Close IAP functionIAP_CMD 0; …...
搭建测试平台开发(一):Django基本配置与项目创建
一、安装Django最新版本 1 pip install django 二、创建Django项目 首先进入要存放项目的目录,再执行创建项目的命令 1 django-admin startproject testplatform 三、Django项目目录详解 1 testplatform 2 ├── testplatform # 项目的容器 3 │ ├──…...
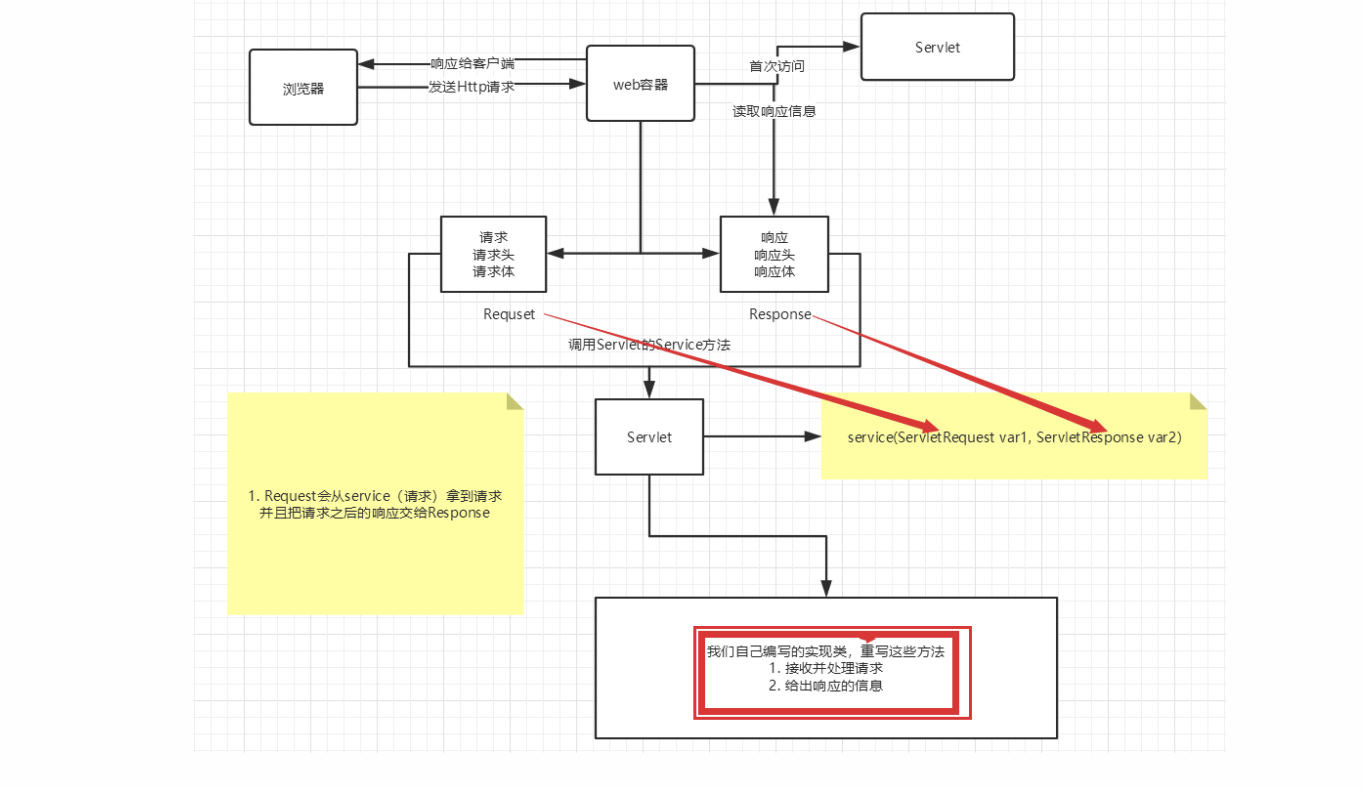
JavaWeb教程笔记
JavaWeb Java Web 1、基本概念 1.1、前言 web开发: web,网页的意思 , www.baidu.com静态web html,css提供给所有人看的数据始终不会发生变化! 动态web 淘宝,几乎是所有的网站;提供给所有人…...

数据库压力测试方法小结
一、前言 在前面的压力测试过程中,主要关注的是对接口以及服务器硬件性能进行压力测试,评估请求接口和硬件性能对服务的影响。但是对于多数Web应用来说,整个系统的瓶颈在于数据库。 原因很简单:Web应用中的其他因素,…...
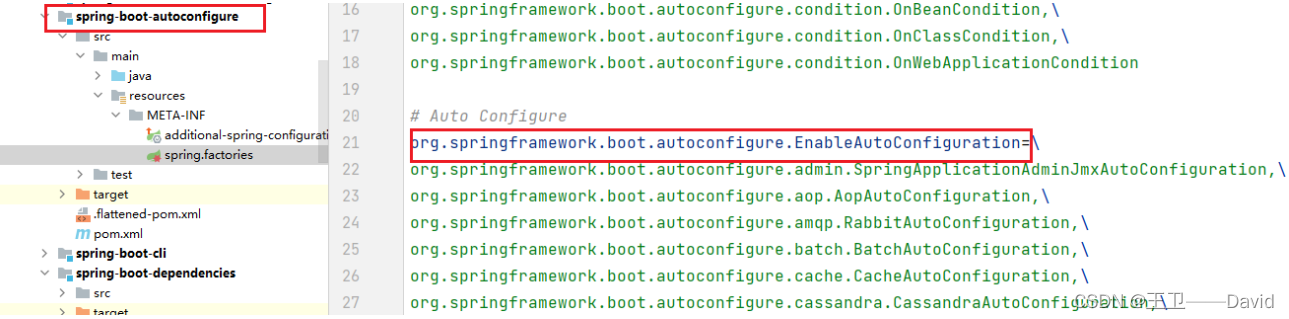
Spring Boot——Spring Boot自动配置原理
系列文章目录 Spring Boot启动原理 Spring Boot自动配置原理 系列文章目录前言一、Spring Boot自动配置原理剖析二、自动配置生效三、总结: 前言 一直在使用Spring Boot特别好奇的是为什么Spring Boot比Spring在项目构建和开发过程中要方便很多,无需编…...
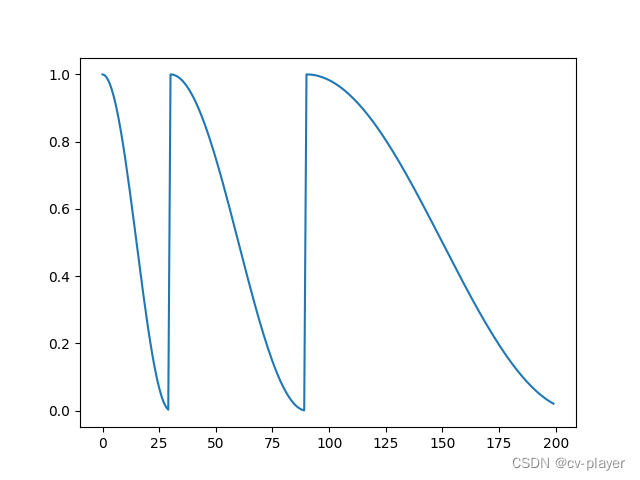
深度学习:Pytorch最全面学习率调整策略lr_scheduler
深度学习:Pytorch最全面学习率调整策略lr_scheduler lr_scheduler.LambdaLRlr_scheduler.MultiplicativeLRlr_scheduler.StepLRlr_scheduler.MultiStepLRlr_scheduler.ConstantLRlr_scheduler.LinearLRlr_scheduler.ExponentialLRlr_scheduler.PolynomialLRlr_sched…...
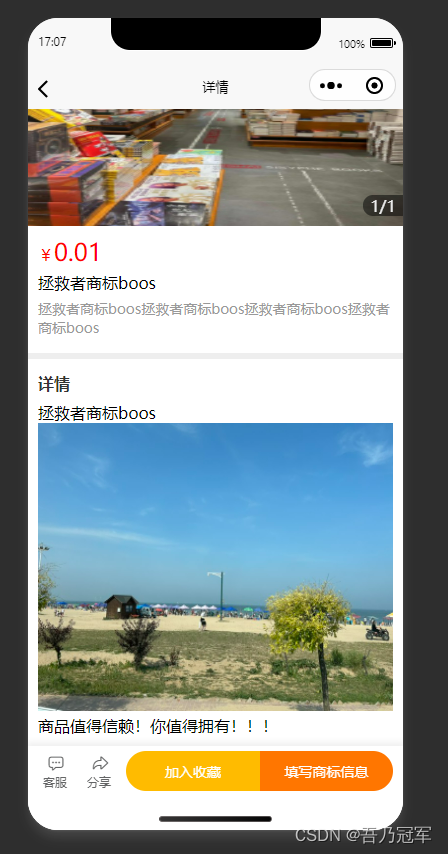
【uniapp】更改富文本编辑器图片大小
代码块 //<view v-html"productDetails"></view><rich-text :nodes"productDetails"></rich-text>// 假设htmlContent字段是后台返回的富文本字段var htmlContent res.result.productDetailsconst regex new RegExp(<img, gi…...
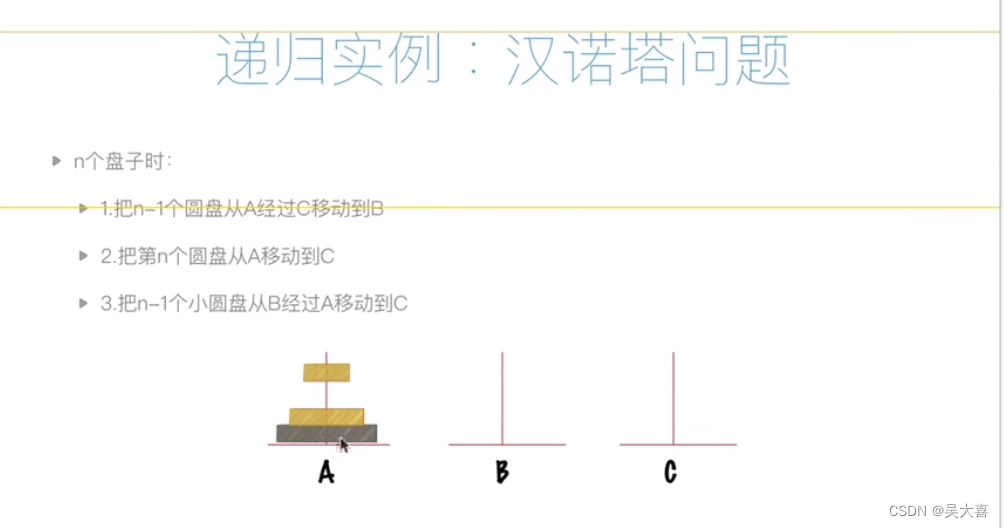
数据结构和算法一(空间复杂度、时间复杂度等算法入门)
时间复杂度: 空间复杂度: 时间比空间重要 递归: 递归特征: 递归案例: 汉诺塔问题: def hanoi(n,A,B,C):if n>0:hanoi(n-1,A,C,B)print("moving from %s to %s"%(A,C))hanoi(n-1,B,A,C)hanoi…...
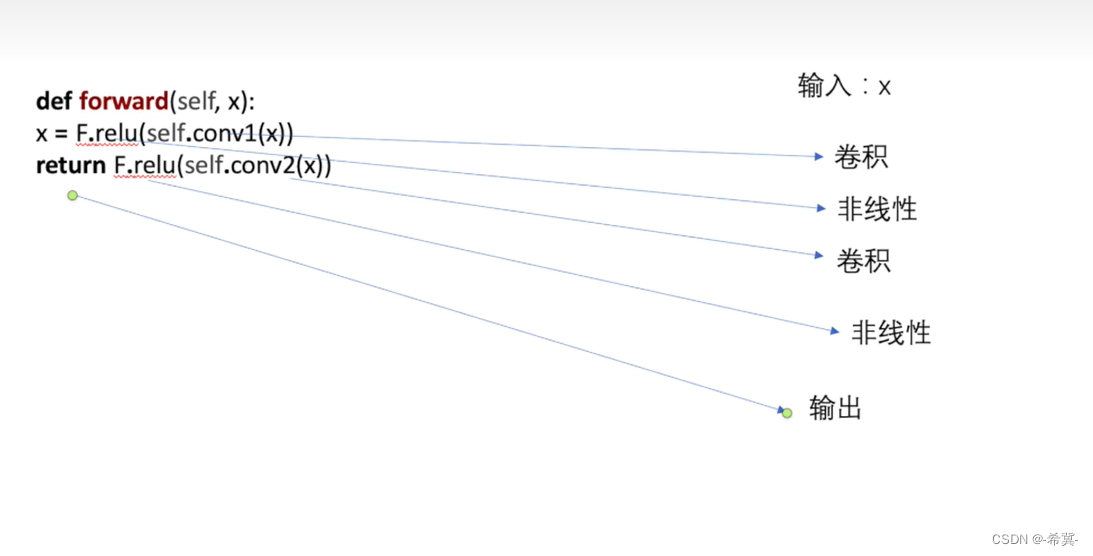
Pytorch深度学习-----神经网络的基本骨架-nn.Module的使用
系列文章目录 PyTorch深度学习——Anaconda和PyTorch安装 Pytorch深度学习-----数据模块Dataset类 Pytorch深度学习------TensorBoard的使用 Pytorch深度学习------Torchvision中Transforms的使用(ToTensor,Normalize,Resize ,Co…...

QT开发快捷键
QT开发快捷键 alt enter // 自动创建类的定义 Ctrl / 注释当前行 或者选中的区域 Ctrl R 运行程序 Ctrl B Build 项目 CtrlShiftF 查找内容 F5 开始调试 ShiftF5 停止调试 F9 设置和取消断点 F10 单步前进 F11 单步进入函数 Shift F11 单步跳出函数 F1 // 查看帮助&#…...
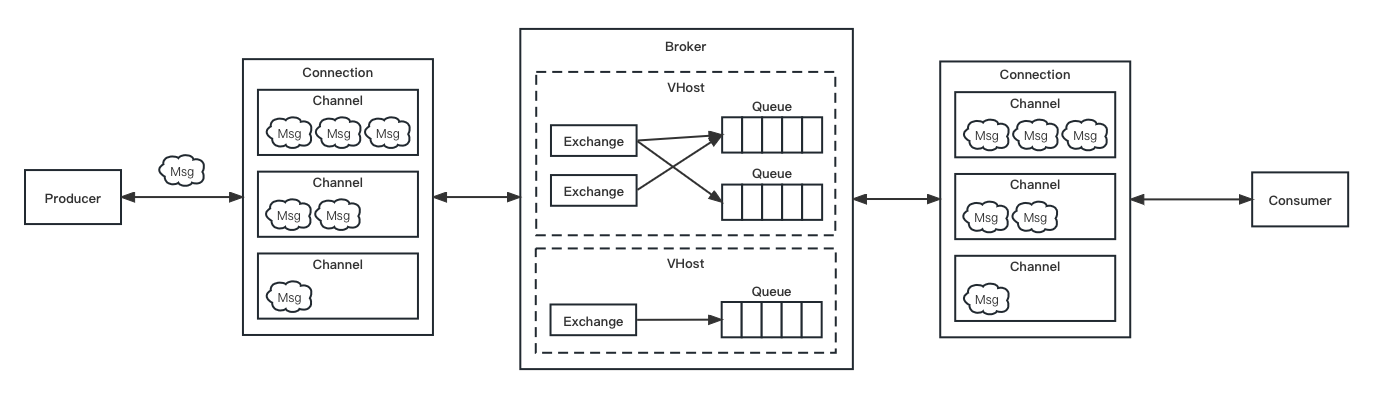
RabbitMQ 教程 | RabbitMQ 入门
👨🏻💻 热爱摄影的程序员 👨🏻🎨 喜欢编码的设计师 🧕🏻 擅长设计的剪辑师 🧑🏻🏫 一位高冷无情的编码爱好者 大家好,我是 DevO…...
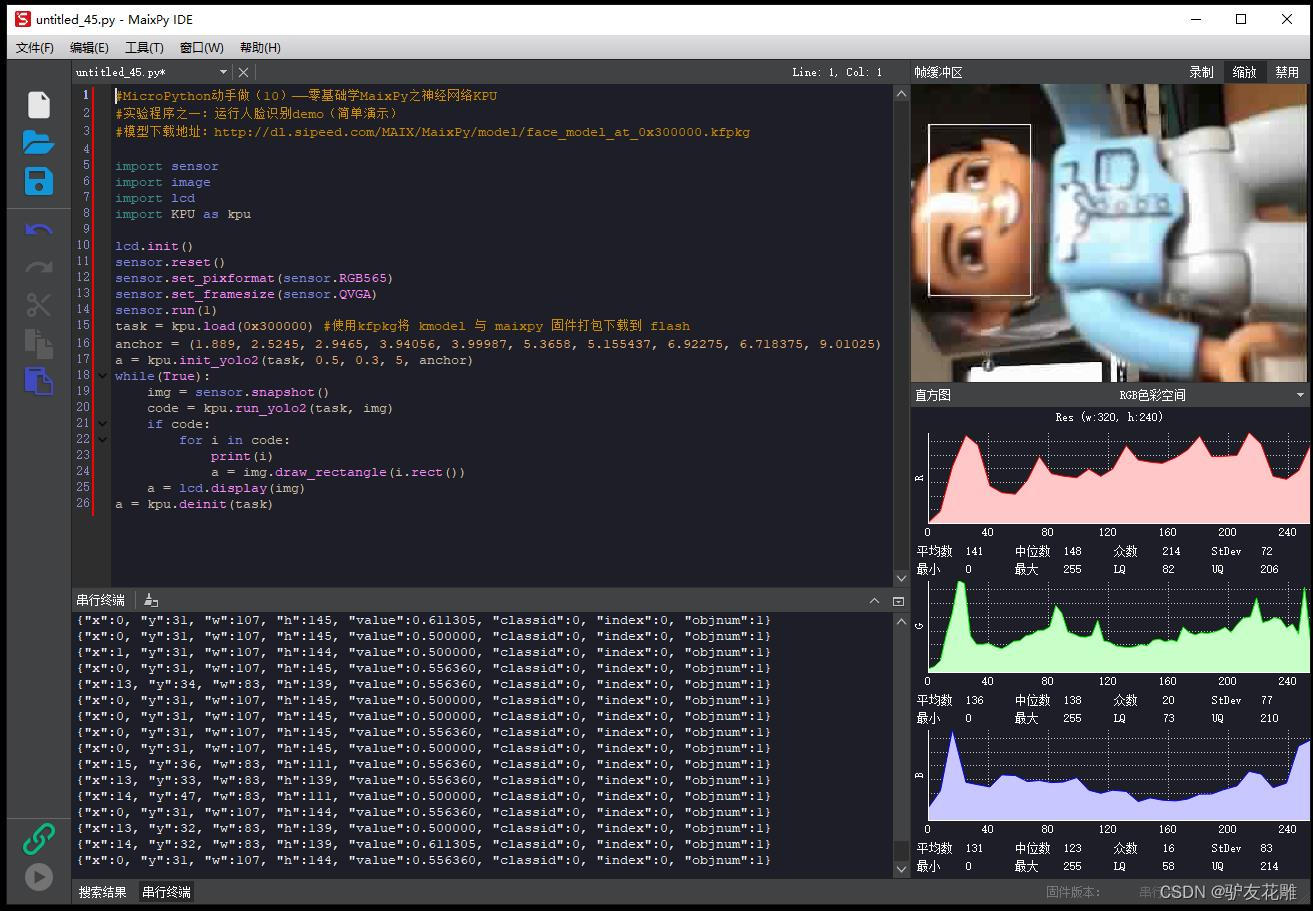
【雕爷学编程】MicroPython动手做(10)——零基础学MaixPy之神经网络KPU2
KPU的基础架构 让我们回顾下经典神经网络的基础运算操作: 卷积(Convolution):1x1卷积,3x3卷积,5x5及更高的卷积 批归一化(Batch Normalization) 激活(Activate) 池化&…...
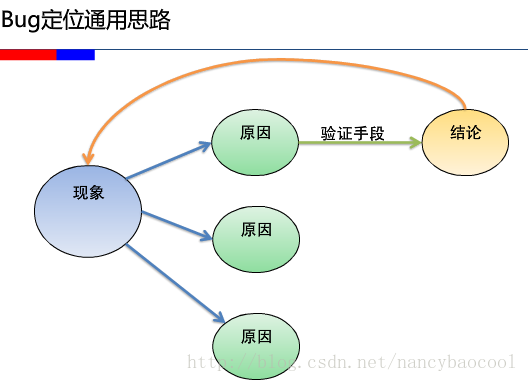
BUG分析以及BUG定位
一般来说bug大多数存在于3个模块: 1、前台界面,包括界面的显示,兼容性,数据提交的判断,页面的跳转等等,这些bug基本都是一眼可见的,不太需要定位,当然也不排除一些特殊情况…...
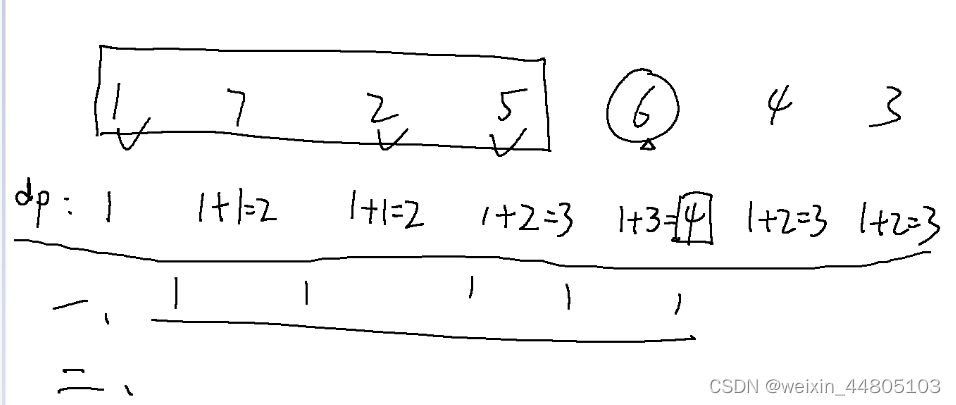
Day46 算法记录| 动态规划 13(子序列)
这里写目录标题 300.最长递增子序列 674. 最长连续递增序列718. 最长重复子数组 300.最长递增子序列 视频解析: 第一层for循环遍历每一个元素, ------- 第二层for循环找到当前元素前面有几个小于该值的元素 结尾需要统计最多的个数 class Solution {pu…...
)
结构型-桥接模式(Bridge Pattern)
概述 桥接模式(Bridge Pattern)是一种结构型设计模式,将抽象部分和实现部分分离,使它们可以独立地变化。桥接模式通过将继承关系转化为关联关系,将抽象部分和实现部分分离开来,从而使它们可以独立地变化。…...
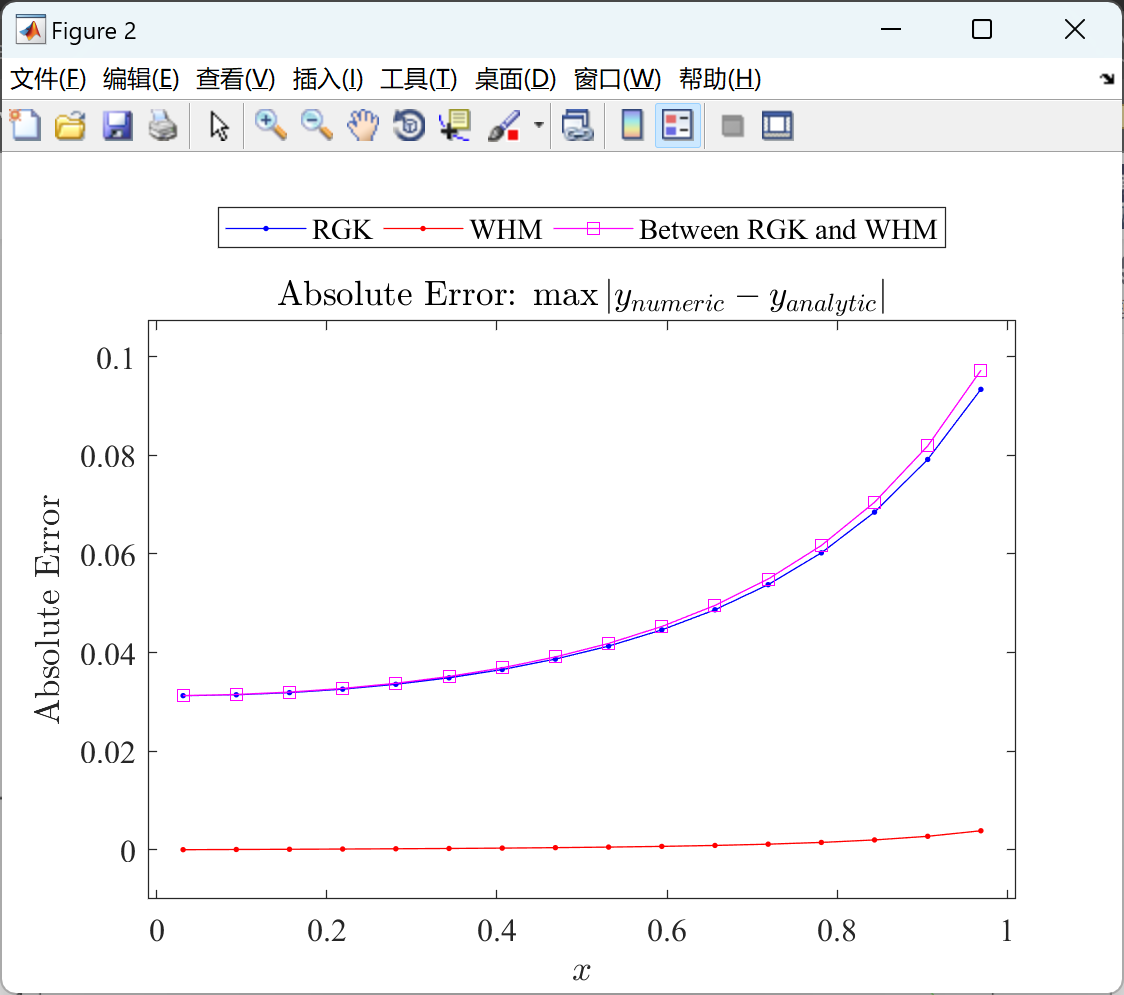
基于小波哈尔法(WHM)的一维非线性IVP测试问题的求解(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码实现 💥1 概述 小波哈尔法(WHM)是一种求解一维非线性初值问题(IVP)的数值方法。它基于小波分析的思想…...
如何读取本地配置文件)
前端(Electron Nodejs)如何读取本地配置文件
使用electron封装了前端界面之后,最终打包为一个客户端(exe)。但是,最近项目组内做CS(c开发)的,想把所有的配置都放进安装目录的配置文件中(比如config.json)。这做法&am…...

没有 telnet 不能测试端口?容器化部署最佳的端口测试方式
写在前面 生产中遇到,整理笔记在容器中没有 telnet ,如何测试远程端口理解不足小伙伴帮忙指正 他的一生告诉我们,不能自爱就不能爱人,憎恨自己也必憎恨他人,最后也会像可恶的自私一样,使人变得极度孤独和悲…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
