2023杭电多校第一场部分题解
还有些没补的题以后回来补。
索引
- 1001
- 1002
- 1003
- 1005
- 1009
- 1010
- 1012
1001
感觉是大暴力题,数据范围给的很小所以每次可以暴力求出两人的路径。枚举路径的交集里的点然后看看两个人在这个点相遇需要的最短时间就可以了。确定了具体的点之后求 4 4 4 次exgcd即可知道答案(分别看两个人是在 来/回 的路上相遇)。
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define maxn 200010
#define inf 999999999#define cn getchar
template<class TY>void read(TY &x){x=0;int f1=1;char ch=cn();while(ch<'0'||ch>'9'){if(ch=='-')f1=-1;ch=cn();}while(ch>='0'&&ch<='9')x=x*10+(ch-'0'),ch=cn(); x*=f1;
}
template<class TY>void write2(TY x){if(x>9)write2(x/10);putchar(x%10+'0');
}
template<class TY>void write(TY x){if(x<0)putchar('-'),x=-x;write2(x);
}
int T,n,m;
struct edge{int y,next;}e[maxn<<1];
int first[maxn],et;
void buildroad(int x,int y){e[++et]=(edge){y,first[x]};first[x]=et;
}
int fa[maxn],dep[maxn];
void dfs(int x){for(int i=first[x];i;i=e[i].next){int y=e[i].y;if(y==fa[x])continue;fa[y]=x;dep[y]=dep[x]+1;dfs(y);}
}
vector<int> A,B;
int sta[maxn],t=0;
void get_path(int S,int T,vector<int> &d){int x=S,y=T;d.clear();while(dep[x]>dep[y])d.push_back(x),x=fa[x];while(dep[x]<dep[y])sta[++t]=y,y=fa[y];while(x!=y){d.push_back(x);x=fa[x];sta[++t]=y;y=fa[y];}d.push_back(x);while(t)d.push_back(sta[t--]);
}
int inA[maxn],inB[maxn];
int exgcd(int a,int b,int &x,int &y){if(b==0){x=1;y=0;return a;}int g=exgcd(b,a%b,y,x);return y-=a/b*x,g;
}
int calc(int a,int l1,int b,int l2){int x,y;a<<=1;b<<=1;int g=exgcd(a,b,x,y);if(abs(l2-l1)%g)return inf;x*=(l2-l1)/g,y*=(l2-l1)/g;x-=x/(b/g)*(b/g);if(x<0)x+=b/g;return a*x+l1;
}int main()
{read(T);while(T--){read(n);read(m);for(int i=1;i<=n;i++)first[i]=0;et=0;for(int i=1;i<n;i++){int x,y;read(x);read(y);buildroad(x,y);buildroad(y,x);}dfs(1);for(int i=1;i<=m;i++){int Sa,Ta,Sb,Tb;read(Sa);read(Ta);read(Sb);read(Tb);get_path(Sa,Ta,A);get_path(Sb,Tb,B);for(int j=1;j<=n;j++)inA[j]=inB[j]=-1;for(int j=0;j<A.size();j++)inA[A[j]]=j;for(int j=0;j<B.size();j++)inB[B[j]]=j;int lenA=A.size()-1,lenB=B.size()-1;int ans=inf;for(int j=1;j<=n;j++)if(inA[j]!=-1&&inB[j]!=-1){ans=min(ans,calc(lenA,inA[j],lenB,inB[j]));if(inA[j]!=0&&inA[j]!=lenA)ans=min(ans,calc(lenA,2*lenA-inA[j],lenB,inB[j]));if(inB[j]!=0&&inB[j]!=lenB)ans=min(ans,calc(lenA,inA[j],lenB,2*lenB-inB[j]));if(inA[j]!=0&&inA[j]!=lenA && inB[j]!=0&&inB[j]!=lenB)ans=min(ans,calc(lenA,2*lenA-inA[j],lenB,2*lenB-inB[j]));}if(ans==inf)puts("-1");else{ans%=lenA*2;if(ans>lenA)write(A[2*lenA-ans]);else write(A[ans]);puts("");}}}
}
1002
很裸的树形dp,感觉应该有原题叭(
设 f i , 0 / 1 / 2 f_{i,0/1/2} fi,0/1/2 表示 i i i 点没有被cover, i i i 自己这里放了路由器, i i i 被某个儿子cover了的情况,转移可以看代码:
#include <bits/stdc++.h>
using namespace std;
#define maxn 200010int n,a[maxn];
vector<int> to[maxn];
long long f[maxn][3];
void dfs(int x,int fa){f[x][0]=f[x][2]=0;f[x][1]=a[x];long long mi=1e10;//注意这个inf值别给太大了,之前给1e18还WA了一发,因为假如有一个点下面挂了很多个叶子那他的f[x][0]就会爆炸了for(int y:to[x])if(y!=fa){dfs(y,x);f[x][0]+=f[y][2];f[x][1]+=min(min(f[y][0],f[y][1]),f[y][2]);if(f[y][1]<=f[y][2])f[x][2]+=f[y][1],mi=0;else f[x][2]+=f[y][2],mi=min(mi,f[y][1]-f[y][2]);}f[x][2]+=mi;
}int main()
{int T;cin>>T;while(T--){scanf("%d",&n);for(int i=1;i<=n;i++)scanf("%d",&a[i]),to[i].clear();for(int i=1;i<n;i++){int x,y;scanf("%d %d",&x,&y);to[x].push_back(y);to[y].push_back(x);}dfs(1,0);printf("%lld\n",min(f[1][1],f[1][2]));}
}
1003
这题其实不是很难,但赛时看过的人少就没怎么看,最后一点时间看的时候就感觉应该可以做,但是dp方向想错了一点,时间不够接着思考了。
实际上就是考虑dp, f l , r , k , r f_{l,r,k,r} fl,r,k,r 表示 [ l , r ] [l,r] [l,r] 区间内消得只剩一张 k k k 类 r r r 级牌的最优贡献,另外多一种状态是 f l , r , 0 , 0 f_{l,r,0,0} fl,r,0,0 表示 [ l , r ] [l,r] [l,r] 区间内啥也不剩的最优贡献,很容易就能得到转移,复杂度是 P ( n 3 m R ) P(n^3mR) P(n3mR),无压力过。
代码如下:
#include <bits/stdc++.h>
using namespace std;
#define ll long longint n,m,R,P;
int a[110],V[110];
ll f[110][110][21][8];
int pw[9];int main()
{int T;cin>>T;while(T--){cin>>n>>m>>R>>P;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=m;i++)cin>>V[i];R=min(R,6);for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)for(int k=0;k<=m;k++)//注意初始化别忘记 f[i][j][0][0] 的情况for(int r=0;r<=R;r++)f[i][j][k][r]=-1e13;for(int i=1;i<=n;i++)f[i][i][a[i]][1]=0,f[i][i][0][0]=V[a[i]];pw[0]=1;for(int i=1;i<=R;i++)pw[i]=pw[i-1]*P;for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++){int j=i+len-1;for(int k=1;k<=m;k++)for(int r=1;r<=R&&(1<<r-1)<=len;r++){for(int p=i;p<j;p++){f[i][j][k][r]=max(f[i][j][k][r],f[i][p][k][r]+f[p+1][j][0][0]);f[i][j][k][r]=max(f[i][j][k][r],f[i][p][0][0]+f[p+1][j][k][r]);f[i][j][k][r]=max(f[i][j][k][r],f[i][p][k][r-1]+f[p+1][j][k][r-1]);}if(f[i][j][k][r]>=0)f[i][j][0][0]=max(f[i][j][0][0],f[i][j][k][r]+1ll*V[k]*pw[r-1]);}}}cout<<f[1][n][0][0]<<'\n';}
}
1005
将每个已知串哈希一下放到map里,每次O(1)查询即可。
但是似乎没有什么很好的环哈希技术,只能先求个最小表示法再用串哈希了。
代码很简单就不贴了。
1009
用鸽巢原理判断一下即可,
1010
x j ≥ x j + 1 x_j\geq x_{j+1} xj≥xj+1可以得到一个很经典的性质: [ a i ≥ x j ] [a_i\geq x_j] [ai≥xj] 的值,只可能形如 1 , 1 , 1 , 0 , 0 , 0 , 0 , . . . 1,1,1,0,0,0,0,... 1,1,1,0,0,0,0,...,也就是至多发生一次转换。
那么也很经典的用线段树来维护就行, a i ≥ x j a_i\geq x_j ai≥xj 时每次操作相当于区间减,每次看看区间内最小值是否 < x j <x_j <xj,是的话暴力进去修改成 a i < x j a_i<x_j ai<xj 类的点,这一类点每次操作相当于区间取反并且 + x j +x_j +xj。
队友写的代码,有空再补。
1012
是一类很经典的博弈的几乎板子题,但我居然没见过啊可恶,
一棵树每次删掉一条边 以及去掉所有不和根节点相连的点,不能操作者败。
考虑SG函数,假如子树是一条链,那么SG值显然是总边数,这个相当于 Nim 游戏只有一堆石子的情况。
对于一个点,如果有多个儿子,先递归进去求他们的SG值,假如一个儿子SG值为 p p p,那么其实可以直接将子树看做一条长度为 p p p 的链,那么这个点的SG值就是 S G x = ⊕ y ∈ s o n ( S G y + 1 ) SG_x=\oplus_{y\in son} (SG_y+1) SGx=⊕y∈son(SGy+1),因为每个儿子的链相当于多了一条边,那么SG值自然就+1,然后根据经典的博弈结论,直接将他们的新SG值异或起来就得到这个点的SG值了。
看回这个题,每次删掉一棵子树+不可操作者获胜其实等价于上面的每次删掉一条边以及对应的子树+不可操作者失败。
所以用一个换根dp求一下每个点的SG值即可求出答案。
代码很简单就不贴了。
相关文章:

2023杭电多校第一场部分题解
还有些没补的题以后回来补。 索引 1001100210031005100910101012 1001 感觉是大暴力题,数据范围给的很小所以每次可以暴力求出两人的路径。枚举路径的交集里的点然后看看两个人在这个点相遇需要的最短时间就可以了。确定了具体的点之后求 4 4 4 次exgcd即可知道答…...

算法38:反转链表【O(n)方案】
一、需求 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2] 输出:[2,1] 示例3ÿ…...

redis基本架构:一个键值数据库包含什么?(这篇文章主要是一个引导的作用)
我们设计一个简单的smpliekv数据库,来体验简直数据库包含什么 体来说,一个键值数据库包括了访问框架、索引模块、操作模块和存储模块四部分(见 下图)。接下来,我们就从这四个部分入手,继续构建我们的 Simpl…...

HIS信息管理系统 HIS源码
HIS(Hospital Information System)是覆盖医院所有业务和业务全过程的信息管理系统。 HIS系统以财务信息、病人信息和物资信息为主线,通过对信息的收集、存储、传递、统计、分析、综合查询、报表输出和信息共享,及时为医院领导及各…...

微信小程序之富文本那些事
文章目录 前言一、video的处理二、img的处理总结 前言 小程序中使用富文本编辑器,由于rich-text受限 部分富文本内容无法渲染或排版错乱。以img和video为例,处理起来让人头疼。网上各种长篇大论,实际上没有任何帮助。接下来我们就一起聊聊im…...

kaggle新赛:RSNA 2023 腹部创伤检测大赛赛题解析(CV)
赛题名称:RSNA 2023 Abdominal Trauma Detection 赛题链接: https://www.kaggle.com/competitions/rsna-2023-abdominal-trauma-detection 赛题背景 腹部钝力创伤是最常见的创伤性损伤类型之一,最常见的原因是机动车事故。腹部创伤可能导致…...
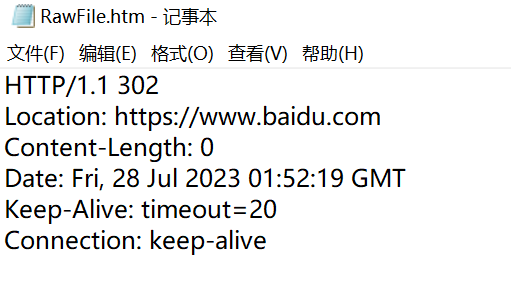
【JavaEE初阶】Servlet (二) Servlet中常用的API
文章目录 HttpServlet核心方法 HttpServletRequest核心方法 HttpServletResponse核心方法 Servlet中常用的API有以下三个: HttpServletHttpServletRequestHttpServletResponse HttpServlet 我们写 Servlet 代码的时候, 首先第一步就是先创建类, 继承自 HttpServlet, 并重写其…...
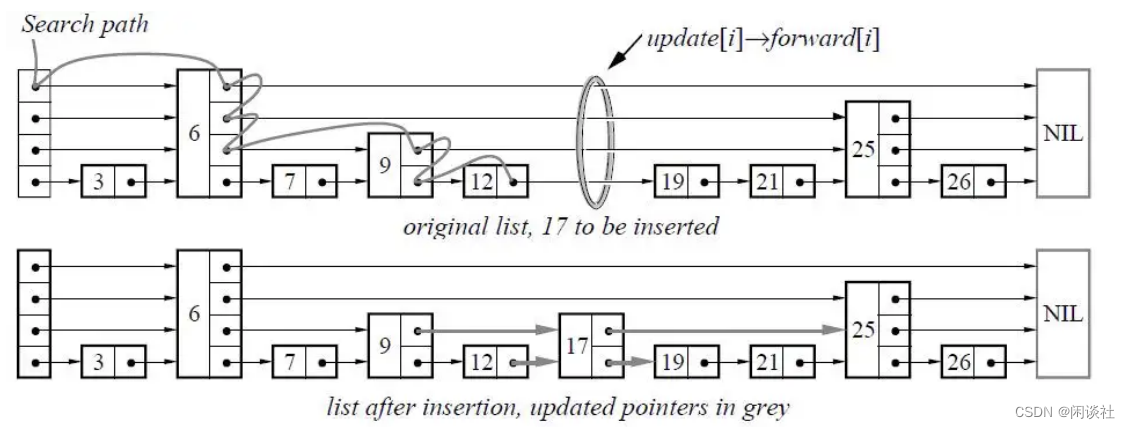
redis 存储原理与数据模型
文章目录 一、redis的存储结构1.1 存储结构1.2 存储转换 二、字典(dict)实现2.1 数据结构2.2 哈希冲突2.3 扩容2.4 缩容2.5 渐进式rehash2.6 scan 命令2.7 expire机制 三、跳表(skiplist)实现3.1 理想跳表3.2 redis跳表 一、redis的存储结构 1.1 存储结构 1.2 存储转换 二、字…...
初识mysql数据库之事务的隔离性
目录 一、理解隔离性 二、隔离级别 1. 不同的隔离级别的简单概述 2. 查看隔离级别 2.1 查看全局隔离级别 2.2 查看会话隔离级别 3. 设置隔离界别 4. 读未提交(Read Uncommitted) 4.1 读未提交测试 5. 读提交(Read Committed&#x…...

今天学学消息队列RocketMQ:消息类型
RocketMQ支持的消息类型有三种:普通消息、顺序消息、延时消息、事务消息。以下内容的代码部分都是基于rocketmq-spring-boot-starter做的。 普通消息 普通消息是一种无序消息,消息分布在各个MessageQueue当中,以保证效率为第一使命。这种消息…...

小程序附件下载并预览功能
一、实现的功能: 1、word、excel、图片等实现下载并预览 2、打开文件后显示文件名称 二、代码: // 判断文件类型whatFileType(url) {let sr url.lastIndexOf("."); // 最后一次出现的位置let fileType url.substr(sr 1); // 截取url的…...

数据库缓存服务——NoSQL之Redis配置与优化
目录 一、缓存概念 1.1 系统缓存 1.2 缓存保存位置及分层结构 1.2.1 DNS缓存 1.2.2 应用层缓存 1.2.3 数据层缓存 1.2.4 硬件缓存 二、关系型数据库与非关系型数据库 2.1 关系型数据库 2.2 非关系型数据库 2.3 关系型数据库和非关系型数据库区别: 2.4 非…...

【雕爷学编程】MicroPython动手做(13)——掌控板之RGB三色灯
知识点:什么是掌控板? 掌控板是一块普及STEAM创客教育、人工智能教育、机器人编程教育的开源智能硬件。它集成ESP-32高性能双核芯片,支持WiFi和蓝牙双模通信,可作为物联网节点,实现物联网应用。同时掌控板上集成了OLED…...

.Net Core上传组件_.Net Core图片上传组件_Uploader7.0
一、.Net Core上传组件Uploader7.0简介 1.当前版本v7.0,前端框架丰富升级 2.前端jquery框架封装,cover.js, 腾讯云cos-js-sdk-v5.min.js 3.后端,支持Asp.Net 和 Asp.Net Core 矿建 4.数据传输模式支持:WebScoket 、Ajax、Form 模式上传到…...

Exadata磁盘损坏导致磁盘组无法mount恢复(oracle一体机磁盘组异常恢复)---惜分飞
Oracle Exadata客户,在换盘过程中,cell节点又一块磁盘损坏,导致datac1磁盘组(该磁盘组是normal方式冗余)无法mount Thu Jul 20 22:01:21 2023 SQL> alter diskgroup datac1 mount force NOTE: cache registered group DATAC1 number1 incarn0x0728ad12 NOTE: ca…...

左值引用与右值引用的区别?右值引用的意义?
左值引用与右值引用的区别?右值引用的意义? 1 区别1.1 功能差异1.2 左值引用1.3 右值引用1.3.1 实现移动语义1.3.2 实现完美转发 2 引用的作用3 区分左值和右值3.1 左值3.2 右值 1 区别 左值引用是对左值的引用;右值引用是对右值的引用。 &…...
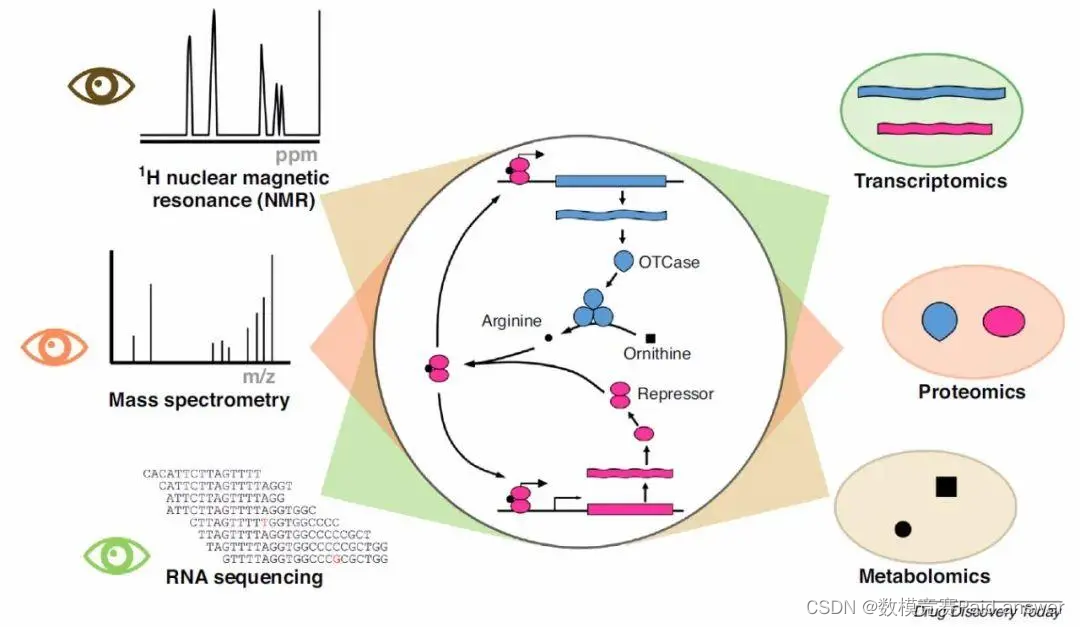
2023年深圳杯数学建模D题基于机理的致伤工具推断
2023年深圳杯数学建模 D题 基于机理的致伤工具推断 原题再现: 致伤工具的推断一直是法医工作中的热点和难点。由于作用位置、作用方式的不同,相同的致伤工具在人体组织上会形成不同的损伤形态,不同的致伤工具也可能形成相同的损伤形态。致伤…...

Vue的router学习
,前端路由的核心是什么呢?改变URL,但是页面不进行整体的刷新。 vue-router是基于路由和组件的 路由用于设定访问路径, 将路径和组件映射起来; 在vue-router的单页面应用中, 页面的路径的改变就是组件的切换; 使用router需要…...
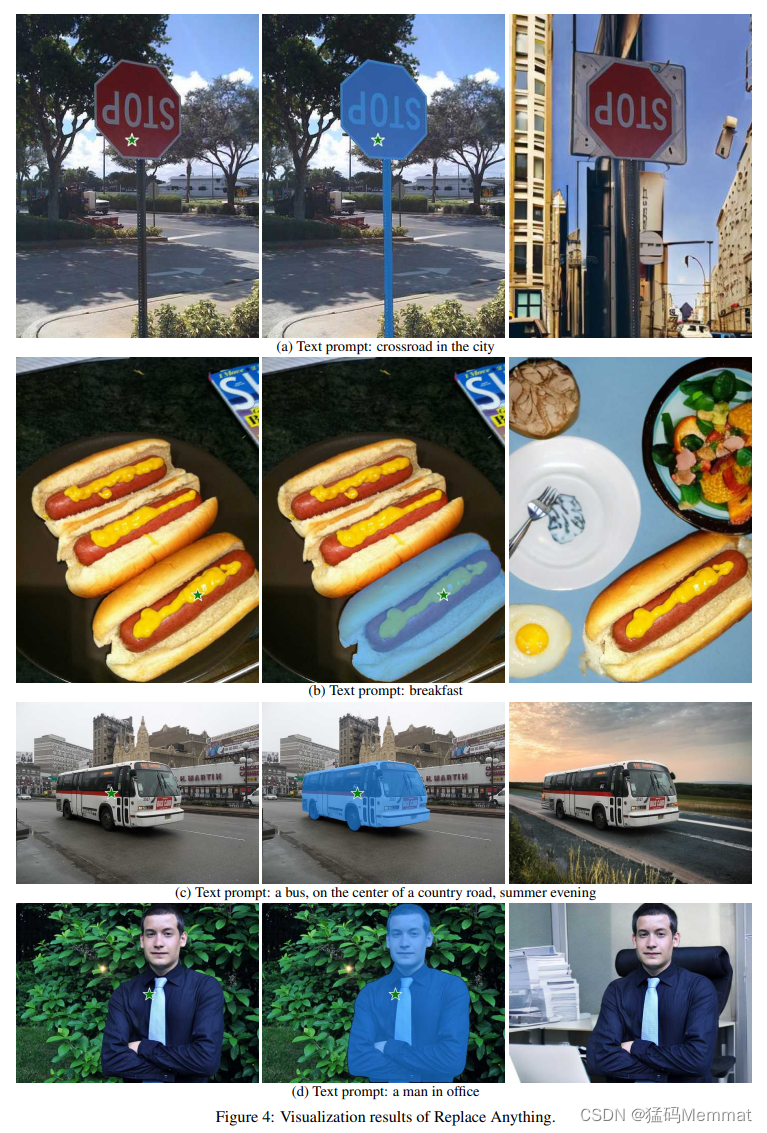
Inpaint Anything: 自动化抹除视频元素
自动化抹除视频元素 不用逐帧抠图,直接SAM Tracking Video Inpainting就能实现自动化抹除奔跑吧idol。 https://github.com/geekyutao/Inpaint-Anything 目录 网站演示参考文献 网站 https://huggingface.co/spaces/InpaintAI/Inpaint-Anything 演示 原理就是&a…...
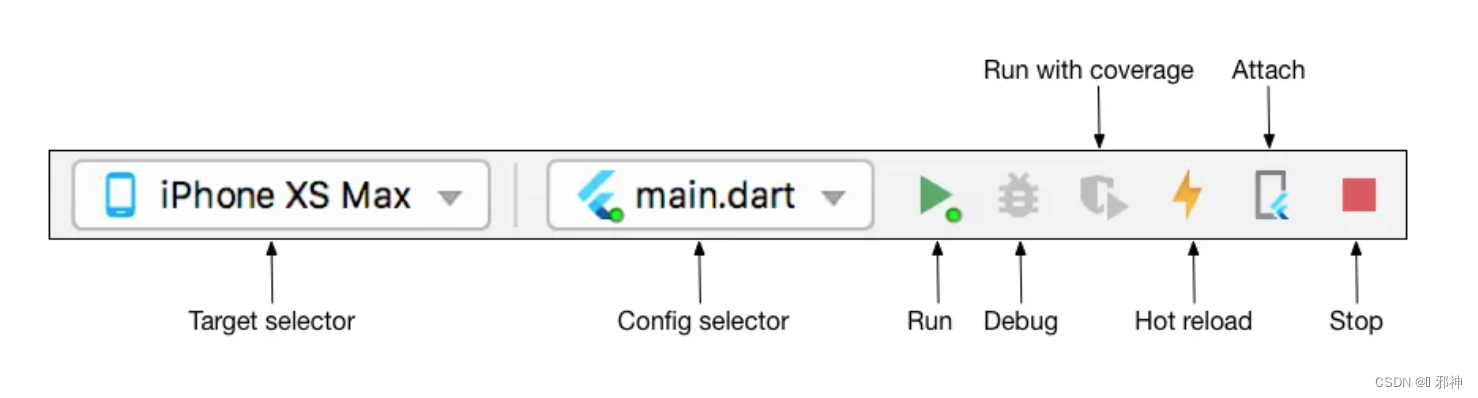
Flutter 开发者工具 Android Studio 开发Flutter应用
Flutter 开发者工具 在 Android Studio 开发Flutter应用 🔥 Android Studio 版本更新 🔥 Android Studio Check for Update Connection failed 解决方案 如果是运行的是32位的android studio需要在andriod studio的启动目录下找到studio.exe.vmoptio…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
