【数据结构】树与森林
目录
树的存储方法
双亲表示法
孩子表示法
孩子兄弟表示法
树、森林与二叉树的转换
树转换成二叉树
森林转换成二叉树
二叉树转换成森林
树与森林的遍历
树的遍历
森林的遍历
树的存储方法
双亲表示法
这种存储结构采用一组连续空间来存储每个结点,同时在每个结点中增设一个伪指针,指示其双亲结点在数组中的位置,根结点下标为0,其伪指针域为-1。

孩子表示法
孩子表示法是将每个结点的孩子结点视为一个线性表,且以单链表作为存储结构,则n个结点就有n个孩子链表(叶结点的孩子链表为空表)。而n个头指针又组成一个线性表,为便于查找,可采用顺序存储结构。

孩子兄弟表示法
孩子兄弟表示法又称二叉树表示法,即以二叉链表作为树的存储结构。孩子兄弟表示法使每个结点包括三部分内容:结点值、指向结点第一个孩子结点的指针,以及指向结点下一个兄弟结点的指针,其中左指针指向第一个孩子,右指针指向第一个兄弟。

孩子兄弟表示法比较灵活,其最大的优点是可以方便地实现树转换为二叉树的操作,易于查找结点的孩子等,但缺点是从当前结点查找其双亲结点比较麻烦。若为每个结点增设一个parent域指向其父结点,则查找结点的父结点也很方便。
孩子兄弟表示法代码如下:
typedef struct CSNode{int data;struct CSNode *firstchild, *nextsibling;
}CSNode,*CSTree;树、森林与二叉树的转换
树转换成二叉树
树转换为二叉树的规则是:每个节点的左指针指向它的第一个孩子,右指针指向它在树中的相邻右兄弟。这种规则也被称为“左孩子右兄弟”表示法。由于根节点在树中没有兄弟,因此树转换得到的二叉树的根节点没有右子树。
将树转换为二叉树的画法可以按照以下步骤进行:
1. 在兄弟节点之间加连线:对于树中的每个节点,将其所有子节点(即兄弟节点)之间用线连接起来。
2. 保留第一个孩子的连线,删除其他孩子的连线:对于每个节点,只保留它与第一个孩子的连线,而删除与其他子节点的连线。
3.顺时针旋转 45°:以树的根节点为轴心,将整个结构顺时针旋转 45°,使得转换后的二叉树符合“左孩子右兄弟”的规则。
示例如下:


森林转换成二叉树
将森林转换为二叉树的规则与树转换为二叉树类似,具体步骤如下:
1. 先将森林中的每棵树分别转换为二叉树,转换规则遵循“左孩子右兄弟”原则,即每个节点的左指针指向其第一个孩子,右指针指向其相邻的右兄弟。
2. 连接各二叉树:由于每棵树转换为二叉树后,其右子树必定为空,因此可以将森林中第二棵树的根节点视为第一棵树根节点的右兄弟,即将第二棵树对应的二叉树作为第一棵二叉树根的右子树;同理,将第三棵树对应的二叉树作为第二棵二叉树根的右子树,依次类推,最终将整个森林连接成一棵二叉树。
二叉树转换成森林
二叉树转换为森林的规则如下:
1. 确定第一棵树:如果二叉树非空,那么二叉树的根节点及其左子树对应森林中的第一棵树。因此,需要将根节点的右链断开。
2. 递归处理剩余部分:断开右链后,二叉树根的右子树可以看作是由森林中除第一棵树之外的其余树转换而来的二叉树。对这个右子树重复上述操作,即继续断开右链,提取下一颗树,直到最后只剩下一棵没有右子树的二叉树为止。
3.转换为树:将每棵提取出的二叉树依次转换为树。最终,这些树组合起来就是原森林。
二叉树转换为树或森林的过程是唯一的。
树与森林的遍历
树的遍历
树的遍历是指按照某种顺序访问树中的每个节点,并且每个节点只被访问一次。主要的遍历方式有两种:
先根遍历
- 如果树非空,先访问根节点。
- 然后依次遍历根节点的每棵子树,在遍历子树时仍然按照“先根后子树”的规则进行。
- 先根遍历的序列与这棵树转换为二叉树后的先序遍历序列相同。
后根遍历:
- 如果树非空,先依次遍历根节点的每棵子树,在遍历子树时仍然按照“先子树后根”的规则进行。
- 遍历完所有子树后,再访问根节点。
- 后根遍历的序列与这棵树转换为二叉树后的中序遍历序列相同。
森林的遍历
森林的遍历方法基于森林和树的递归定义,主要有两种遍历方式:
先序遍历森林:
- 如果森林非空,先访问森林中第一棵树的根节点。
- 然后先序遍历第一棵树中根节点的子树森林(即第一棵树的子树部分)。
- 最后,先序遍历除去第一棵树之后剩余的树构成的森林。
中序遍历森林:
- 如果森林非空,先中序遍历森林中第一棵树的根节点的子树森林(即第一棵树的子树部分)。
- 然后访问第一棵树的根节点。
- 最后,中序遍历除去第一棵树之后剩余的树构成的森林。
相关文章:

【数据结构】树与森林
目录 树的存储方法 双亲表示法 孩子表示法 孩子兄弟表示法 树、森林与二叉树的转换 树转换成二叉树 森林转换成二叉树 二叉树转换成森林 树与森林的遍历 树的遍历 森林的遍历 树的存储方法 双亲表示法 这种存储结构采用一组连续空间来存储每个结点,同时…...

跟着StatQuest学知识08-RNN与LSTM
一、RNN (一)简介 整个过程权重和偏置共享。 (二)梯度爆炸问题 在这个例子中w2大于1,会出现梯度爆炸问题。 当我们循环的次数越来越多的时候,这个巨大的数字会进入某些梯度,步长就会大幅增加&…...

【SpringCloud】Eureka的使用
3. Eureka 3.1 Eureka 介绍 Eureka主要分为两个部分: EurekaServer: 作为注册中心Server端,向微服务应用程序提供服务注册,发现,健康检查等能力。 EurekaClient: 服务提供者,服务启动时,会向 EurekaS…...

nuxt3 seo优化
在 Nuxt3 中,通过 nuxtjs/seo、nuxtjs/sitemap 和 nuxtjs/robots 模块可以生成包含动态链接的站点地图(sitemap.xml),但具体是“实时生成”还是“部署时生成”,取决于你的配置方式和数据更新频率。以下是具体分析&…...

初识MySQL · 数据类型
目录 前言: 数值类型 文本、二进制数据类型 时间类型 String类型 前言: 对于MySQL来说,是一门编程语言,可能定义不是那么的严格,但是对于MySQL来说也是拥有自己的数据类型的,比如tinyint,…...

【Go】数组
数组Array 重点: 数组是值类型 注意点: 1. 数组:是同一种数据类型的固定长度的序列。2. 数组定义:var a [len]int,比如:var a [5]int,数组长度必须是常量,且是类型的组成部分。一旦定义&…...

QT图片轮播器(QT实操学习2)
1.项目架构 1.UI界面 2.widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget>#define TIMEOUT 1 * 1000 QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent n…...

深度解析衡石科技HENGSHI SENSE嵌入式分析能力:如何实现3天快速集成
嵌入式分析成为现代SaaS的核心竞争力 在当今SaaS市场竞争中,数据分析能力已成为产品差异化的关键因素。根据Bessemer Venture Partners的最新调研,拥有深度嵌入式分析功能的SaaS产品,其客户留存率比行业平均水平高出23%,ARR增长速…...

杂草YOLO系列数据集4000张
一份开源数据集——杂草YOLO数据集,该数据集适用于农业智能化、植物识别等计算机视觉应用场景。 数据集详情 训练集:3,664张高清标注图像测试集:180张多样性场景样本验证集:359张严格筛选数据 下载链接 杂草YOLO数据集分…...

Mybatis_Plus中常用的IService方法
查询 方法名 查询记录总数 /*** 查询总记录数** see Wrappers#emptyWrapper()*/default long count() {return count(Wrappers.emptyWrapper());} 方法实现 Testpublic void testGetCount(){long count userService.count();System.out.println("总记录数:&…...

Flink/Kafka在python中的用处
一、基础概念 1. Apache Kafka 是什么? 核心功能:Kafka 是一个分布式流处理平台,主要用于构建实时数据管道和流式应用程序。核心概念: 生产者(Producer):向 Kafka 发送数据的程序。…...

Vue 2 探秘:visible 和 append-to-body 是谁的小秘密?
🚀 Vue 2 探秘:visible 和 append-to-body 是谁的小秘密?🤔 父组件:identify-list.vue子组件:fake-clue-list.vue 嘿,各位前端探险家!👋 今天我们要在 Vue 2 的代码丛林…...

机器学习的一百个概念(1)单位归一化
前言 本文隶属于专栏《机器学习的一百个概念》,该专栏为笔者原创,引用请注明来源,不足和错误之处请在评论区帮忙指出,谢谢! 本专栏目录结构和参考文献请见[《机器学习的一百个概念》 ima 知识库 知识库广场搜索&…...

SpringCould微服务架构之Docker(5)
Docker的基本操作: 镜像相关命令: 1.镜像名称一般分两部分组成:[repository]:[tag]。 2. 在没有指定tag时,默认是latest,代表着最新版本的镜像。 镜像命令的案例: 镜像操作常用的命令: dock…...

JVM 如何打破双亲委派模型?
虽然双亲委派模型是 Java 类加载机制的推荐实现方式,但在某些情况下,为了实现特定的功能,可能需要打破双亲委派模型。以下是一些常见的打破双亲委派模型的方法和场景: 1. 重写 loadClass 方法 (不推荐): 原理: java.l…...

DeepSeek结合MCP Server与Cursor,实现服务器资源的自动化管理
MCP Server是最近AI圈子中又一个新的热门话题。很多用户都通过结合大语言模型、MCP Server,实现了一些工具流的自动化,例如,你只需要给出文字指令,就可以让Blender自动化完成建模的工作。你有没有想过,利用MCP来让AI A…...

SpringAI与JBoltAI深度对比:从工具集到企业级AI开发范式的跃迁
一、Java生态下大模型开发的困境与需求 技术公司的能力断层 多数企业缺乏将Java与大模型结合的标准开发范式,停留在碎片化工具使用阶段。 大模型应用需要全生命周期管理能力,而不仅仅是API调用。 工具集的局限性 SpringAI作为工具集的定位࿱…...

后端返回了 xlsx 文件流,前端怎么下载处理
当后端返回一个 .xlsx 文件流时,前端可以通过 JavaScript 处理这个文件流并触发浏览器下载。 实现步骤 发送请求获取文件流: 使用 fetch 或 axios 等工具向后端发送请求,确保响应类型设置为 blob(二进制数据流)。 创建…...
)
一文读懂Python之json模块(33)
一、json模块介绍 json模块的功能是将序列化的json数据从文件里读取出来或者存入文件。json是一种轻量级的数据交换格式,在大部分语言中,它被理解为数组(array)。 json模块序列化与反序列化的过程分别是 encoding和 decoding。e…...

Python中multiprocessing的使用详解
1.实现多进程 代码实现: from multiprocessing import Process import datetime import timedef task01(name):current_timedatetime.datetime.now()start_timecurrent_time.strftime(%Y-%m-%d %H:%M:%S). "{:03d}".format(current_time.microsecond //…...

强化学习与神经网络结合(以 DQN 展开)
目录 基于 PyTorch 实现简单 DQN double DQN dueling DQN Noisy DQN:通过噪声层实现探索,替代 ε- 贪心策略 Rainbow_DQN如何计算连续型的Actions 强化学习中,智能体(Agent)通过与环境交互学习最优策略。当状态空间或动…...

函数式组件中的渲染函数 JSX
在 Vue.js 和 React 等现代前端框架中,函数式组件已成为一种非常流行的设计模式。函数式组件是一种没有内部状态和生命周期方法的组件,其主要功能是接受 props 并渲染 UI。随着这些框架的演进,渲染函数和 JSX(JavaScript XML&…...

北斗导航 | 基于因子图优化的GNSS/INS组合导航完好性监测算法研究,附matlab代码
以下是一篇基于因子图优化(FGO)的GNSS/INS组合导航完好性监测算法的论文框架及核心内容,包含数学模型、完整Matlab代码及仿真分析基于因子图优化的GNSS/INS组合导航完好性监测算法研究 摘要 针对传统卡尔曼滤波在组合导航完好性监测中对非线性与非高斯噪声敏感的问题,本文…...

飞书电子表格自建应用
背景 coze官方的插件不支持更多的飞书电子表格操作,因为需要自建应用 飞书创建文件夹 创建应用 开发者后台 - 飞书开放平台 添加机器人 添加权限 创建群 添加刚刚创建的机器人到群里 文件夹邀请群 创建好后,就可以拿到id和key 参考教程: 创…...

深度学习四大核心架构:神经网络(NN)、卷积神经网络(CNN)、循环神经网络(RNN)与Transformer全概述
目录 📂 深度学习四大核心架构 🌰 知识点概述 🧠 核心区别对比表 ⚡ 生活化案例理解 🔑 选型指南 📂 深度学习四大核心架构 第一篇: 神经网络基础(NN) 🌰 知识点概述…...
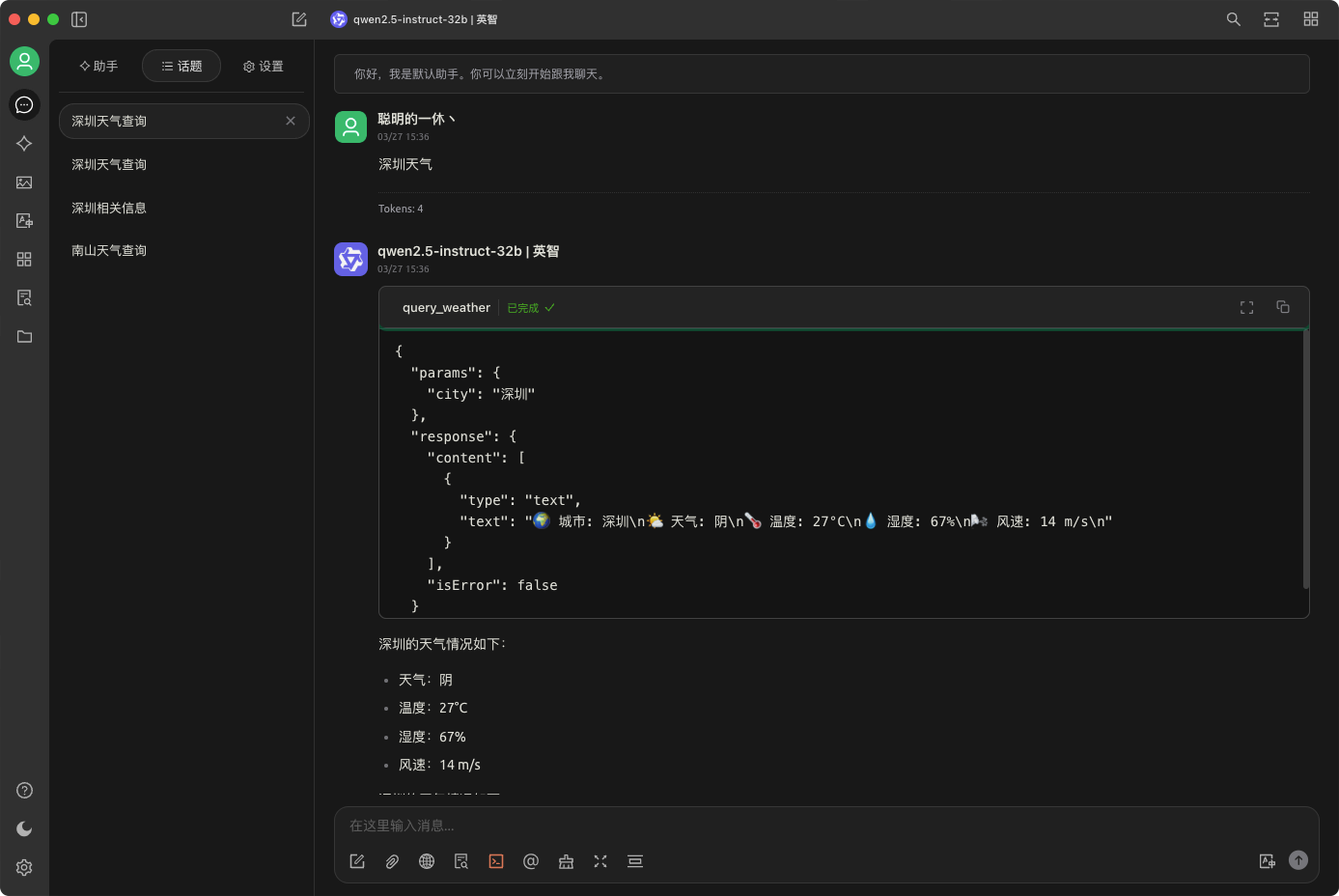
MCP Server 实现一个 天气查询
Step1. 环境配置 安装 uv curl -LsSf https://astral.sh/uv/install.sh | shQuestion: 什么是 uv 呢和 conda 比有什么区别? Answer: 一个用 Rust 编写的超快速 (100x) Python 包管理器和环境管理工具,由 Astral 开发。定位为 pip 和 venv 的替代品…...

《强化学习基础概念:四大模型与两大损失》
强化学习基础概念一、策略模型1. 策略的定义2. 策略的作用3.策略模型 二、价值模型1. 价值函数的定义(1)状态值函数(State Value Function)(2)动作值函数(Action Value Function) 2.…...

Headless Chrome 优化:减少内存占用与提速技巧
在当今数据驱动的时代,爬虫技术在各行各业扮演着重要角色。传统的爬虫方法往往因为界面渲染和资源消耗过高而无法满足大规模数据采集的需求。本文将深度剖析 Headless Chrome 的优化方案,重点探讨如何利用代理 IP、Cookie 和 User-Agent 设置实现内存占用…...

知识就是力量——HELLO GAME WORD!
你好!游戏世界! 简介环境配置前期准备好文章介绍创建头像小功能组件安装本地中文字库HSV颜色空间音频生成空白的音频 游戏UI开发加载动画注册登录界面UI界面第一版第二版 第一个游戏(贪吃蛇)第二个游戏(俄罗斯方块&…...

电脑连不上手机热点会出现的小bug
一、问题展示 注意: 不要打开 隐藏热点 否则他就会在电脑上 找不到自己的热点 二、解决办法 把隐藏热点打开即可...
