机器学习(八):K-Means聚类原理与实战
声明:未经允许禁止转载与抄袭。
前言
k k k均值( k k k-means)聚类算法是一种经典的无监督聚类算法,本文将深入解析其理论原理,并在真是数据集上进行算法实践,话不多说,请看下文。
算法原理
给定样本集 D = { x 1 , x 2 , … , x m } D=\left\{\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_m\right\} D={x1,x2,…,xm},其中每个样本 x i \mathbf{x}_i xi都由一个向量表示,例如以周志华老师西瓜书中的西瓜数据集为例,每个样本都包含两个属性密度和含糖量,这两个属性值组成的向量便是该样本的向量表示。
k k k均值算法旨在将样本集 D D D划分为 k k k个簇,即 C = { C 1 , C 2 , … , C k } C=\left\{C_1,C_2,\ldots,C_k\right\} C={C1,C2,…,Ck},使得每个样本都被划分到与其距离最小的簇中。用数学来刻画就是, k k k均值算法希望能够最小化所划分的 k k k个簇的平方误差,即:
argmin C ∑ i = 1 k ∑ x ∈ C i ∥ x − μ i ∥ 2 2 \text{argmin}_{C} \sum_{i=1}^k \sum_{\mathbf{x} \in C_i}\left\|\mathbf{x}-\mathbf{\mu}_i\right\|_2^2 argminCi=1∑kx∈Ci∑∥x−μi∥22
其中 μ i = 1 ∣ C i ∣ ∑ x ∈ C i x \boldsymbol{\mu}_i=\frac{1}{\left|C_i\right|} \sum_{\mathbf{x} \in C_{\boldsymbol{i}}} \mathbf{x} μi=∣Ci∣1∑x∈Cix 表示簇 C i C_i Ci 的均值向量, x \mathbf{x} x表示簇 C i C_i Ci中的样本。
k k k均值算法事先设定数据集 D D D要划分为 k k k个簇,初始化时,会先从数据集 D D D中随机挑选 k k k个样本作为各个簇的初始均值向量(簇中心)。然后遍历所有样本,分别计算各个样本与各个簇中心的距离,并将样本划分到与距离最小的簇中。待到所有样本都划分完毕后,将各个簇样本向量的均值向量作为新的簇均值向量,重复上述的步骤,直到上一轮所有的簇中心均值向量与本轮计算的结果相同为止。该算法的具体算法流程如下:

需要注意的是,实际计算过程中为避免计算时间过长,该算法的终止条件不可能这样严苛。西瓜书中给出了两种方案:
- 设置一个最大轮数。
- 设置均值向量的变化阈值,若新簇中心与旧簇中心之间的距离不超过该阈值即可,而不是严格不变。
对于 k k k均值聚类算法而言,数据集的预处理和 k k k值的选取同样十分重要,可以参考博客【机器学习】K-means(非常详细),限于篇幅原因,本文就不详细展开。
算法实践
本文在鸢尾花数据集上进行 k k k均值聚簇算法的实践。
基于最大轮数终止的 k k k均值聚类算法实现如下所示,两个向量之间的距离计算本文采用了余弦距离。
import numpy as np
from scipy.spatial.distance import cdistclass KMeansModel:def rand_pick(self, x, k):"""随机选取k个簇中心"""n = x.shape[0]indices = np.random.choice(n, k, replace=False)return x[indices]def calculate_distance(self, x, centers):"""计算簇中心与数据样本之间的余弦距离centers: 簇中心数据 (k, d)x: 样本 (N, d)"""return cdist(x, centers, metric="cosine")def get_centers(self, k, x, y):"""根据计算结果重新计算簇中心y: 根据距离将数据集划分的标签数组 (N)"""centers = np.zeros((k, x.shape[1]))for label in range(k):centers[label] = np.mean(x[y == label], axis=0)return centersdef get_label(self, dis):"""根据距离矩阵将每个样本划分到距离最小的簇中心"""return np.argmin(dis, axis=-1)def cluster(self, x, k, times):"""进行KMeans聚类x: 数据样本 (N, d)k: 类别数tims: 迭代次数"""# 随机选取k个作为初始簇中心centers = self.rand_pick(x, k)for _ in range(times):# 计算各个样本到簇中心的距离dis = self.calculate_distance(x, centers)# 根据距离矩阵将样本进行划分y = self.get_label(dis)# 重新计算新的簇中心centers = self.get_centers(k, x, y)return y
在鸢尾花数据集上,设置的实验参数为 k = 3 k=3 k=3, t i m e s = 500 times=500 times=500,即将整个数据集聚为 3 3 3个簇,算法迭代 500 500 500轮终止。
算法额外对比了基于sklearn库实现的 k k k均值聚簇算法的效果,为更直观的展示,本文对数据集进行PCA降维,下图从左到右分别是真实标签、本文模型的聚类结果、基于sklearn算法的聚类结果。从结果可以看出,本文实现的模型在鸢尾花数据集上效果还是不错的。

结语
以上便是本文的全部内容,如果感觉不错可以支持一下,若有任何问题敬请批评指正。
相关文章:

机器学习(八):K-Means聚类原理与实战
声明:未经允许禁止转载与抄袭。 前言 k k k均值( k k k-means)聚类算法是一种经典的无监督聚类算法,本文将深入解析其理论原理,并在真是数据集上进行算法实践,话不多说,请看下文。 算法原理 …...

基于yolo11的BGA图像目标检测
1.产生图像数据的分辨率 2.产生图像的大小 3.产生图像是黑白或是RGB彩色 灰度图像,达到识别要求,减少计算量 4.标注数据的精准程度 1.模型标注后,少量标注全部人工校验,大量数据抽检,部分人工检验 2.明确边界框贴合…...

分享一些新版GPT-4o使用方式!能多模态生图!
目前GPT-4o的整体测评,真的很惊艳。 不知道又有多少人因为OpenAI的这次更新而失业,当然只要AI用得好,会有更多人因之而受益!很多人表示不知道怎么用,对于门外汉来说,4o似乎有点高端。 今天就给大家介绍几…...

【stm32--HAL库DMA+USART+空闲中断不定长收发数据】
串口通信-Hal库实现不定长度收发,DMAUSART DMA串口STM32CUBEMX配置(工程创建)基础配置时钟配置工程配置 代码编写现象 DMA 在正式配置之前,我们先来一起简单了解一下DMA。DMA(Direct Memory Access,直接内…...

【算法中的数学】欧拉筛埃氏筛
筛质数 题目传送门 题目链接 一、题目描述 给定一个正整数 n,请你求出 1∼n 中质数的个数。 输入格式 共一行,包含整数 n。 输出格式 共一行,包含一个整数,表示 1∼n 中质数的个数。 数据范围 1 ≤ n ≤ 10⁶ 输入样例&am…...

【SPP】蓝牙串口配置中LM互操作性要求深度解析
在蓝牙协议栈中,链路管理器(Link Manager, LM)承担着链路建立、安全管理、功耗控制等核心功能。对于串行端口配置文件(SPP)而言,LM 的互操作性直接影响连接稳定性、数据安全性和设备功耗。本文基于蓝牙核心…...

Java迭代器【设计模式之迭代器模式】
目录 一.前言 二.正文 1.我写的类为什么不能使用增强for(迭代器遍历) 2.代码健全性——迭代器常见的两个Exception 1.NoSuchElementException 2.ConcurrentModificationException 三.后言 一.前言 本篇面向对象主要为和我一样的小白,主要是对迭代器模式的浅…...
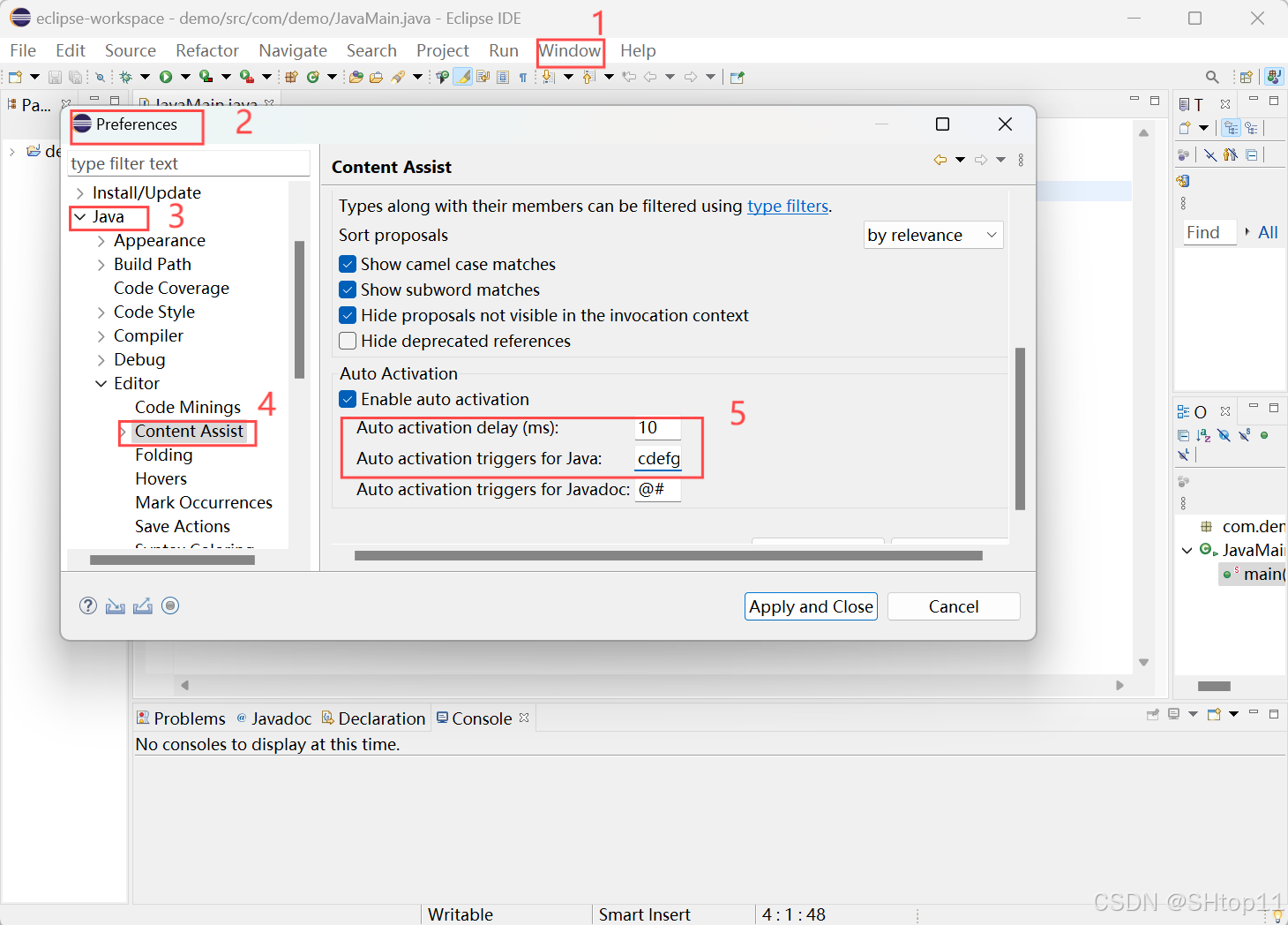
Eclipse IDE
创建新的Java项目和类 在 Eclipse IDE 中创建一个新的 Java 项目和 Java 类的步骤如下: 1. 创建新的 Java 项目 打开 Eclipse IDE。在菜单栏中,点击 File > New > Java Project。在弹出的对话框中,输入项目名称(例如&…...

【面试篇】多线程
基础概念 线程的生命周期有哪些状态?它们是如何转换的? 答案:线程的生命周期有以下六种状态: 新建(New):线程被创建但尚未启动,此时线程对象已被分配内存空间,相关属性已…...

MySQL表缺乏主键或唯一索引对主从复制的深度影响及解决方案
引言 在MySQL数据库设计中,主键(Primary Key)和唯一索引(Unique Index)不仅是数据完整性的基石,更是主从复制(Replication)可靠性的关键。然而,许多开发者或DBA因历史遗…...

计算机视觉算法实战——基于YOLOv8的自动驾驶障碍物实时感知系统
✨个人主页欢迎您的访问 ✨期待您的三连 ✨ ✨个人主页欢迎您的访问 ✨期待您的三连 ✨ ✨个人主页欢迎您的访问 ✨期待您的三连✨ 引言:自动驾驶感知系统的关键挑战 自动驾驶技术正以前所未有的速度重塑交通出行方式ÿ…...

【boost搜索引擎】下
boost搜索引擎 1. 编写搜索引擎模块 Searcher2. 编写 http_server 模块3. 编写前端模块4. 添加日志5. 补充 去掉暂停词6. 项目扩展方向 1. 编写搜索引擎模块 Searcher 这一模块主要提供建立索引,以及收到用户的发起的http请求通过Get方法提交的搜索关键字ÿ…...

数据结构优化DP总结
单调栈:Codeforces Round 622 (Div. 2) C2. Skyscrapers (hard version) 简单来讲就是最后需要呈现出一个单峰数组,使得总高度最高。 最开始想到暴力枚举每一个元素都充当最高的“单峰”,但是这里的 n 过大,这样枚举肯定会TLE。 …...

[Linux系统编程]进程间通信—system V
进程间通信—system V 1. System V 共享内存(Shared Memory)1.1 共享内存的建立过程1.2 共享内存函数2. System V 消息队列(Message Queues)3. System V 信号量(Semaphores)4. 总结前言: 之前所提的管道通信是基于文件的,OS没有做过多的设计工作。 system V 进程间通信…...

Eigen库几何模块深度解析与实践指南
Eigen库几何模块深度解析与实践指南 a. Eigen几何模块概述 i. 几何模块的核心功能 在三维空间中,几何变换是描述物体位置和姿态变化的基础,其数学基础涵盖了线性代数中的矩阵运算等知识。Eigen库的几何模块为这些变换提供了高效且便捷的实现方式。 旋转、平移和缩放是三维…...

第十四届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组(部分题解)
文章目录 前言日期统计题意: 冶炼金属题意: 岛屿个数题意: 子串简写题意: 整数删除题意: 总结 前言 一年一度的🏀杯马上就要开始了,为了取得更好的成绩,好名字写了下前年2023年蓝桥…...

C语言常见3种排序
主要是三种排序方法:冒泡排序、选择排序、插入排序。 文章目录 一、冒泡排序 1.代码: 2.工作原理: 3.具体过程: 二、选择排序 1.代码 2. 工作原理 3.具体过程: 三、插入排序 1.代码 2.工作原理 3.具体过程 总结 一、…...
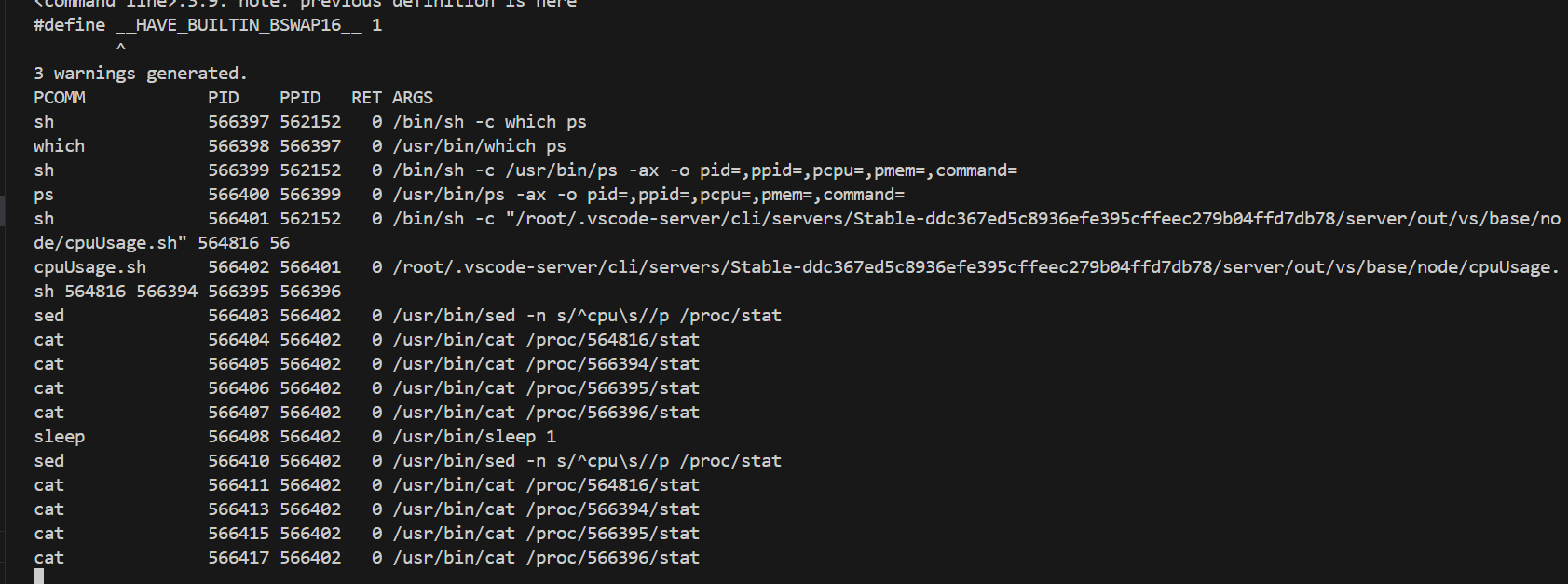
分析sys高问题的方法总结
一、背景 sys高的问题往往属于底层同学更需要关注的问题,sys高的问题往往表现为几种情况,一种是瞬间的彪高,一种是持续的彪高。这篇博客里,我们总结一下常用的分析方法和分析工具的使用来排查这类sys高的问题。 二、通过mpstat配…...

智谱发布AI Agent“AutoGLM沉思”,开启AI“边想边干”新时代
近日,智谱正式推出全新AI Agent产品——AutoGLM沉思,标志着人工智能从“思考”迈向“执行”的关键突破。该智能体不仅具备深度研究能力,还能自主完成实际操作,真正实现“边想边干”的智能化应用。 在演示环节,智谱展示…...

使用Leaflet对的SpringBoot天地图路径规划可视化实践-以黄花机场到橘子洲景区为例
目录 前言 一、路径规划需求 1、需求背景 2、技术选型 3、功能简述 二、Leaflet前端可视化 1、内容布局 2、路线展示 3、转折路线展示 三、总结 前言 在当今数字化与智能化快速发展的时代,路径规划技术已经成为现代交通管理、旅游服务以及城市规划等领域的…...

【小兔鲜】day02 Pinia、项目起步、Layout
【小兔鲜】day02 Pinia、项目起步、Layout 1. Pinia2. 添加Pinia到Vue项目3. 案例:Pinia-counter基础使用3.1 Store 是什么?3.2 应该在什么时候使用 Store? 4. Pinia-getters和异步action4.1 getters4.2 action如何实现异步 1. Pinia Pinia 是 Vue 的专…...

PyTorch 激活函数
激活函数是神经网络中至关重要的组成部分,它们为网络引入了非线性特性,使得神经网络能够学习复杂模式。PyTorch 提供了多种常用的激活函数实现。 常用激活函数 1. ReLU (Rectified Linear Unit) 数学表达式: PyTorch实现: torch.nn.ReLU(inplaceFals…...

魔塔社区使用llamafactory微调AI阅卷试题系统
启动 LLaMA-Factory 1. 安装 LLaMA-Factory 执行安装指令 git clone --depth 1 https://github.com/hiyouga/LLaMA-Factory.git cd LLaMA-Factory pip install -e ".[torch,metrics]"解决依赖冲突 如果遇到依赖冲突,可使用以下命令安装,不…...

Java面试黄金宝典29
1. 什么是普通索引和唯一性索引 定义: 普通索引:是最基本的索引类型,它为数据表中的某一列或多列建立索引,以加快数据的查询速度。它不限制索引列的值重复,允许存在多个相同的值。唯一性索引:在普通索引的基…...

git `switch` 命令详解与实用示例
文章目录 git switch 命令详解与实用示例git switch vs git checkoutgit switch 用法1. 切换到已有分支2. 创建并切换到新分支3. 切换到上一个分支4. 切换到远程分支(自动创建本地分支并追踪远程)5. 放弃未提交的修改并切换分支 总结 git switch 命令详解…...

Oracle中文一二三四排序【失败】
原文地址: Oracle数据库如何对中文的一二三四五六七八九十数进行正序排列排序_中文数字排序-CSDN博客 自定义排序函数 -- 自定义中文映射阿拉伯数字函数 CREATE OR REPLACE FUNCTION P_ORDER_CHINESE_TO_ARABIC(V_NUM VARCHAR2) RETURN NUMBER IS BEGIN-- 根据…...

AWS S3 和 Lambda 使用
目录: AWS概述 EMR Serverless AWS VPC及其网络 关于AWS网络架构的思考 AWS S3 和 Lambda 使用 本文将通过一个实例来说明如何使用 AWS S3 和 Lambda。 使用场景:通过代码将文件上传到S3,该文件需要是公开访问的,并对上传的文件进…...

Mysql 在什么样的情况下会产生死锁?
在 MySQL 中,死锁是指两个或多个事务相互等待对方释放锁,导致所有相关事务无法继续执行的情况。死锁会影响数据库的并发性能,因此需要及时检测并处理。假设有两个事务 T1 和 T2: 事务 T1 首先锁定 表 A 的行 1。然后尝试锁定 表 B…...

符号秩检验
内容来源 非参数统计(第2版) 清华大学出版社 王星 褚挺进 编著 符号秩检验 在符号检验的基础上,增加了数据绝对值大小的信息 检验统计量 用一个简单的例子来说明 样本数据 X i , i 1 , ⋯ , 6 X_i,i1,\cdots,6 Xi,i1,⋯,6 如下 X …...

RainbowDash 的 Robot
H RainbowDash 的 Robot - 第七届校赛正式赛 —— 补题 题目大意: 给一个 n ∗ m n*m n∗m 的二维网格,在第 i i i 列中,前 a i a_i ai 单元格被阻断,无法通行,即 [ 1 , a i ] [1,a_i] [1,ai] 。 一个机器人正…...
