[数据结构]图krusakl算法实现
目录
- Kruskal算法
Kruskal算法
我们要在连通图中去找生成树
连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
生成树:一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。也就是用最少的边(n-1条边)连通起来。
最小生成树:构成生成树的这些边加起来权值最小,也就是最小的成本让这N个顶点连通,最小生成树不唯一。
连通图中的每一棵生成树,都是原图的一个极大无环子图,即:从其中删去任何一条边,生成树就不在连通;反之,在其中引入任何一条新边,都会形成一条回路。
若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条:
- 只能使用图中的
权值最小的边来构造最小生成树 - 只能使用恰好n-1条边来连接图中的n个顶点
- 选用的n-1条边不能构成回路
构造最小生成树的方法:Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。
贪心算法:是指在问题求解时,总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体最优的的选择,而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。
Kruskal算法和Prim算法求出来的一定是最优解吗?——不一定

因此要选出最小的边,然后进行连接
在这里判定是否成环的关键是并查集
代码实现:
W Kruskal(Self& minTree)
{minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(_vertexs.size());for (auto& e : minTree._matrix){e.resize(_vertexs.size(), MAX_W);}// 先根据边的权值进行排序priority_queue<Edge, vector<Edge>, greater<Edge>> pq;for (size_t i = 0; i < _vertexs.size(); ++i){for (size_t j = 0; j < _vertexs.size(); ++j){if (i < j && _matrix[i][j] != MAX_W){// pq.push(_matrix[i][j]); 不是这样pq.push(Edge(i, j, _matrix[i][j]));}}}W total = W();size_t i = 1; // 最初有一个顶点// 从最小的边开始进行选择(贪心)UnionFindSet ufs(_vertexs.size());while (i < _vertexs.size() && !pq.empty()){Edge min = pq.top();pq.pop();// 判断是否会构成一个回路,不会则添加到最小生成树中if (ufs.FindRoot(min._srci) != ufs.FindRoot(min._dsti)){cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":" << _matrix[min._srci][min._dsti] << endl;minTree._AddEdge(min._srci, min._dsti, min._w);total += min._w;ufs.Union(min._srci, min._dsti);++i;}}if (i == _vertexs.size()){return total;}else{return W();}
}
完整代码:
namespace matrix // 领接矩阵存储
{template <class V, class W, W MAX_W = INT_MAX, bool Direction = false> // Vertex, Weight, Direction表示有向图还是无向图class Graph{typedef Graph<V, W, MAX_W, Direction> Self; // 表示子图public:Graph(){}Graph(const V* vertex, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; ++i){_vertexs.push_back(vertex[i]);_indexMap[vertex[i]] = i; // map<V, int>second存的是对应的编号}_matrix.resize(n);for (int i = 0; i < n; ++i){_matrix[i].resize(n, MAX_W);}}size_t GetVertexIndex(const V& v){auto ret = _indexMap.find(v);if (ret != _indexMap.end()){return ret->second;}else{assert(false);return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_AddEdge(srci, dsti, w);}void _AddEdge(size_t srci, size_t dsti, const W& w){_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void Print(){// 顶点for (size_t i = 0; i < _vertexs.size(); ++i){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;// 矩阵// 横下标cout << " ";for (size_t i = 0; i < _vertexs.size(); ++i){//cout << i << " ";printf("%4d", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); ++i){cout << i << " "; // 竖下标for (size_t j = 0; j < _matrix[i].size(); ++j){//cout << _matrix[i][j] << " ";if (_matrix[i][j] == MAX_W){//cout << "* ";printf("%4c", '*');}else{//cout << _matrix[i][j] << " ";printf("%4d", _matrix[i][j]);}}cout << endl;}cout << endl;}void BFS(const V& src){size_t srci = GetVertexIndex(src);// 队列和标记数组queue<int> q;vector<bool> visited(_vertexs.size(), false); // 标记数组int levelSize = 1; // 保证一层 一层的打印q.push(srci);visited[srci] = true;size_t n = _vertexs.size();while (!q.empty()){for (int i = 0; i < levelSize; ++i){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";// 把front顶点的邻接顶点入队列for (size_t i = 0; i < n; ++i){if (_matrix[front][i] != MAX_W) // 不是无穷大就是相连的{if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size(); // 下一层的数据个数}cout << endl;}void _DFS(size_t srci, vector<bool> visited){cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;// 找srci相邻的没有访问过的点,深度遍历for (size_t i = 0; i < _vertexs.size(); ++i){if (_matrix[srci][i] != MAX_W && visited[i] = false){_DFS(i, visited);}}}void DFS(const V& src){size_t srci = GetVertexIndex(src);vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);}struct Edge{size_t _srci;size_t _dsti;W _w;Edge(size_t srci, size_t dsti, const W& w): _srci(srci), _dsti(dsti), _w(w){}bool operator>(const Edge& e) const{return _w > e._w;}};W Kruskal(Self& minTree){minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(_vertexs.size());for (auto& e : minTree._matrix){e.resize(_vertexs.size(), MAX_W);}// 先根据边的权值进行排序priority_queue<Edge, vector<Edge>, greater<Edge>> pq;for (size_t i = 0; i < _vertexs.size(); ++i){for (size_t j = 0; j < _vertexs.size(); ++j){if (i < j && _matrix[i][j] != MAX_W){// pq.push(_matrix[i][j]); 不是这样pq.push(Edge(i, j, _matrix[i][j]));}}}W total = W();size_t i = 1; // 最初有一个顶点// 从最小的边开始进行选择(贪心)UnionFindSet ufs(_vertexs.size());while (i < _vertexs.size() && !pq.empty()){Edge min = pq.top();pq.pop();// 判断是否会构成一个回路,不会则添加到最小生成树中if (ufs.FindRoot(min._srci) != ufs.FindRoot(min._dsti)){cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] << ":" << _matrix[min._srci][min._dsti] << endl;minTree._AddEdge(min._srci, min._dsti, min._w);total += min._w;ufs.Union(min._srci, min._dsti);++i;}}if (i == _vertexs.size()){return total;}else{return W();}}private:vector<V> _vertexs; // 顶点集合map<V, int> _indexMap; // 顶点映射下标vector<vector<W>> _matrix;// 存储边的关系};void TestGraph(){Graph<char, int, INT_MAX, true> g("0123", 4);g.AddEdge('0', '1', 1);g.AddEdge('0', '3', 4);g.AddEdge('1', '3', 2);g.AddEdge('1', '2', 9);g.AddEdge('2', '3', 8);g.AddEdge('2', '1', 5);g.AddEdge('2', '0', 3);g.AddEdge('3', '2', 6);g.Print();}void TestBDFS() {string a[] = { "张三", "李四", "王五", "赵六", "周七" };Graph<string, int> g1(a, sizeof(a) / sizeof(string));g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.AddEdge("王五", "周七", 30);g1.Print();g1.BFS("张三");}void TestGraphMinTree(){const char* str = "abcdefghi";Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);//g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);Graph<char, int> kminTree;cout << "Kruskal:" << g.Kruskal(kminTree) << endl;//kminTree.Print();/*Graph<char, int> pminTree;cout << "Prim:" << g.Prim(pminTree, 'a') << endl;pminTree.Print();*/}
}
相关文章:

[数据结构]图krusakl算法实现
目录 Kruskal算法 Kruskal算法 我们要在连通图中去找生成树 连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。 生成树:一个连通图的最小…...

SQL122 删除索引
alter table examination_info drop index uniq_idx_exam_id; alter table examination_info drop index full_idx_tag; 描述 请删除examination_info表上的唯一索引uniq_idx_exam_id和全文索引full_idx_tag。 后台会通过 SHOW INDEX FROM examination_info 来对比输出结果。…...

QEMU学习之路(5)— 从0到1构建Linux系统镜像
QEMU学习之路(5)— 从0到1构建Linux系统镜像 一、前言 参考:从内核到可启动镜像:0到1构建你的极简Linux系统 二、linux源码获取 安装编译依赖 sudo apt install -y build-essential libncurses-dev flex bison libssl-dev li…...

node ---- 解决错误【Error: error:0308010C:digital envelope routines::unsupported】
1. 报错 在 Node.js 18.18.0 的版本中,遇到以下错误: this[kHandle] new _Hash(algorithm, xofLen);^ Error: error:0308010C:digital envelope routines::unsupported这个错误通常发生在运行项目或构建时,尤其是在使用 Webpack、Vite 或其他…...

蓝桥杯——走迷宫问题(BFS)
这是一个经典的BFS算法 1. BFS算法保证最短路径 核心机制:广度优先搜索按层遍历所有可能的路径,首次到达终点的路径长度即为最短步数。这是BFS的核心优势。队列的作用:通过队列按先进先出的顺序处理节点,确保每一步探索的都是当…...

详解 Redis repl_backlog_buffer(如何判断增量同步)
一、repl_backlog_buffer 复制积压缓冲区(Replication Backlog Buffer) 是一个环形内存区域(Ring Buffer),用于临时保存主节点最近写入的写命令,以支持从节点断线重连后的增量同步。 1.1 三个复制偏移量 …...

服务器虚拟化技术深度解析:医药流通行业IT架构优化指南
一、服务器虚拟化的定义与原理 (一)技术定义:从物理到虚拟的资源重构 服务器虚拟化是通过软件层(Hypervisor)将物理服务器的CPU、内存、存储、网络等硬件资源抽象为逻辑资源池,分割成多个相互隔离的虚拟机…...

使用PyTorch实现ResNet:从残差块到完整模型训练
ResNet(残差网络)是深度学习中的经典模型,通过引入残差连接解决了深层网络训练中的梯度消失问题。本文将从残差块的定义开始,逐步实现一个ResNet模型,并在Fashion MNIST数据集上进行训练和测试。 1. 残差块(…...

Scala相关知识学习总结5
1、多维数组 定义: val arr Array.ofDim[Double](3,4) 表示二维数组中有三个一维数组,每个一维数组有四个元素。 2、列表 List 不可变 List:默认不可变,可创建有序且可重复的列表,可使用:从右向左增加数据…...

Day1:前端项目uni-app壁纸实战
uni-app官网下载HBuilder。 uni-app快速上手 | uni-app官网 点击HBuilder 安装 新建项目 工具——插件安装 安装uni-app(vue3) 我们先来准备一下: 先在wallpaper下新建目录 我已经建过了 同样,再在common下建images和style目录&…...

光谱相机的光谱数据采集原理
光谱相机的光谱数据采集原理基于分光技术和光电信号转换,通过将入射光按波长分解并记录各波段的强度信息,最终生成包含空间和光谱维度的数据立方体。以下是详细原理分解: 1. 分光技术:将复合光分解为单色光 光谱相机…...

《算法笔记》10.3小节——图算法专题->图的遍历 问题 A: 第一题
题目描述 该题的目的是要你统计图的连通分支数。 输入 每个输入文件包含若干行,每行两个整数i,j,表示节点i和j之间存在一条边。 输出 输出每个图的联通分支数。 样例输入 1 4 4 3 5 5样例输出 2 分析: 由于题目没给出范围࿰…...

python中的{}
注意,如果要创建空集合,只能使用 set() 函数实现。因为直接使用一对 {},Python 解释器会将其视为一个空字典。 Python中集合set和字典dict的用法区别_python创建set变量和dict区别-CSDN博客...
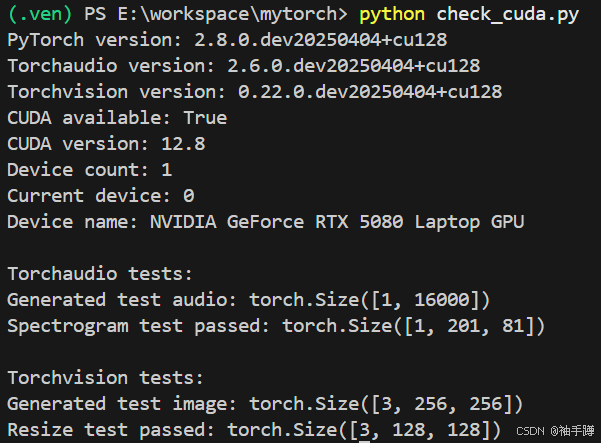
宏碁笔记本电脑擎7PRO搭载的 NVIDIA RTX 5080 显卡安装pytorch
宏碁笔记本电脑擎7PRO搭载的 NVIDIA RTX 5080 显卡是一款高性能移动 GPU,基于 NVIDIA 最新的 Blackwell 架构设计,通过修正架构(Blackwell)、显存类型与带宽(GDDR7、960GB/s)、Tensor Core 与 RT Core 全面…...

html+css+js 实现一个贪吃蛇小游戏
目录 游戏简介 游戏功能与特点 如何玩转贪吃蛇 游戏设计与实现 HTML结构 JavaScript核心实现 代码结构: 效果 关于“其他游戏” 游戏简介 贪吃蛇是一款经典的单人小游戏,玩家通过控制蛇的移动,吃掉食物来增加长度,避免撞…...
API接口解析)
淘宝按图搜索商品(拍立淘)API接口解析
以下是关于淘宝按图搜索商品(拍立淘)API的深度解析指南,结合官方文档和开发者经验整理,包含调用方法、参数详解、返回结果解析及常见问题处理: 一、API核心接口说明 1. 接口名称 官方接口:taobao.image.…...

Python爬虫生成CSV文件的完整流程
引言 在当今数据驱动的时代,网络爬虫已成为获取互联网数据的重要工具。Python凭借其丰富的库生态系统和简洁的语法,成为了爬虫开发的首选语言。本文将详细介绍使用Python爬虫从网页抓取数据并生成CSV文件的完整流程,包括环境准备、网页请求、…...

21.OpenCV获取图像轮廓信息
OpenCV获取图像轮廓信息 在计算机视觉领域,识别和分析图像中的对象形状是一项基本任务。OpenCV 库提供了一个强大的工具——轮廓检测(Contour Detection),它能够帮助我们精确地定位对象的边界。这篇博文将带你入门 OpenCV 的轮廓…...

医学图像分割效率大幅提升!U-Net架构升级,助力精度提升5%!
在医学图像分割领域,U-Net模型及其变体的创新应用正在带来显著的性能提升和效率优化。最新研究显示,通过引入结构化状态空间模型(SSM)和轻量级LSTM(xLSTM)等技术,VMAXL-UNet模型在多个医学图像数…...

智能设备运行监控系统
在工业 4.0 与智能制造浪潮下,设备运行效率与稳定性成为企业竞争力的核心要素。然而,传统设备管理模式面临数据采集分散、状态分析滞后、维护成本高昂等痛点。为破解这些难题,设备运行监控系统应运而生,通过融合智能传感、5G 通信…...

详细分析单例模式
目录 1.单例模式的定义 2.单例模式的实现方式 1.饿汉模式 2.懒汉模式 (1)线程不安全的问题怎么解决? (2)直接对整个getInstance方法代码块加锁吗? (3)那对if语句加锁不就行了吗…...

Windwos的DNS解析命令nslookup
nslookup 解析dns的命令 有两种使用方式,交互式&命令行方式。 交互式 C:\Users\Administrator>nslookup 默认服务器: UnKnown Address: fe80::52f7:edff:fe28:35de> www.baidu.com 服务器: UnKnown Address: fe80::52f7:edff:fe28:35de非权威应答:…...

服务器报错:xxx/libc.so.6: version `GLIBC_2.32‘ not found
/lib/x86_64-linux-gnu/libc.so.6: version GLIBC_2.32 not found (required by ./aima-sim-app-main) 解决思路 根据错误信息,您的应用程序 aima-sim-app-main 和 libmujoco.so.3.1.6 库依赖于较新的 GNU C Library (glibc) 版本(如 GLIBC_2.32, GLIBC…...

Flutter之页面布局一
目录: 1、页面布局一2、无状态组件StatelessWidget和有状态组件StatefulWidget2.1、无状态组件示例2.2、有状态组件示例2.3、在 widget 之间共享状态1、使用 widget 构造函数2、使用 InheritedWidget3、使用回调 3、布局小组件3.1、布置单个 Widget3.2、容器3.3、垂…...

架构思维: 数据一致性的两种场景深度解读
文章目录 Pre案例数据一致性问题的两种场景第一种场景:实时数据不一致不要紧,保证数据最终一致性就行第二种场景:必须保证实时一致性 最终一致性方案实时一致性方案TCC 模式Seata 中 AT 模式的自动回滚一阶段二阶段-回滚二阶段-提交 Pre 架构…...

大数据knox网关API
我们过去访问大数据组件,如sparkui,hdfs的页面,以及yarn上面看信息是很麻烦的一件事。要记每个端口号,比如50070,8090,8088,4007,如果换到另一个集群,不同版本࿰…...
)
UI测试(2)
1、HTML 是用来描述网页的一种语言。 指的是超文本标记语言 (Hyper Text Markup Language) ,HTML 不是一种编程语言,而是一种标记语言 (markup language) 负责定义页面呈现的内容:标签语言:<标签名>标签值<标签名>&am…...

【Tauri2】015——前端的事件、方法和invoke函数
目录 前言 正文 准备 关键url 获取所有命令 切换主题set_theme 设置大小 获得版本version 名字name 监听窗口移动 前言 【Tauri2】005——tauri::command属性与invoke函数-CSDN博客https://blog.csdn.net/qq_63401240/article/details/146581991?spm1001.2014.3001.…...

密码学基础——分组密码的运行模式
前面的文章中文我们已经知道了分组密码是一种对称密钥密码体制,其工作原理可以概括为将明文消息分割成固定长度的分组,然后对每个分组分别进行加密处理。 下面介绍分组密码的运行模式 1.电码本模式(ECB) 2.密码分组链接模式&…...

Android SELinux权限使用
Android SELinux权限使用 一、SELinux开关 adb在线修改seLinux(也可以改配置文件彻底关闭) $ getenforce; //获取当前seLinux状态,Enforcing(表示已打开),Permissive(表示已关闭) $ setenforce 1; //打开seLinux $ setenforce 0; //关闭seLinux二、命令查看sel…...
