数据结构（五)——AVL树（平衡二叉搜索树)

目录

前言

AVL树概念

AVL树的定义

AVL树的插入

右旋转

左旋转

左右双旋

右左双旋

插入代码如下所示

AVL树的查找

AVL树的遍历

AVL树的节点个数以及高度

判断平衡

AVL树代码如下所示

小结

---

前言

前面我们在数据结构中介绍了二叉搜索树，其中提到了二叉搜索树的缺陷：极端情况下时间复杂度会坍缩成O(N)，如何解决它不够稳定这个问题呢？我们发现，只要让二叉树成为一个满二叉树，就可以很好的控制它在查找的过程中的时间复杂度为O(logN)，接下来就让我们一起来学习平衡二叉树当中的AVL树吧。

参考文章：

据结构（四）——二叉搜索树的实现（C++版）

AVL树概念

AVL树是一个平衡二叉搜索树，它的发明者是前苏联的两位科学家G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表，因此我们用他们两个的名字的首字母命名。

它具备以下性质：

1.左右子树高度差不超过1，.它的左右子树都是AVL树

2.它的左子树节点上的值小于根节点上的值，它的右子树节点上的值大于根节点上的值，即左子树<根节点<右子树

3.查找的时间复杂度是O(N)

为了方便理解，我们在这里引入平衡因子的概念：

引入平衡因子的作用是，我们可以通过控制平衡因子来判平衡，然后对AVL树进行调整

AVL树的定义

#include<iostream>
using namespace std;#include<assert.h>template<class K,class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:private:Node* _root=nullptr;
};

我们可以看到，相比于二叉搜索树，我们对AVL树的定义多了一个父节点的指针，同时引入了平衡因子bf，引入父节点的指针是因为我们需要通过父节点的指针找到上一个节点，然后通过不断向上调整，直到调整到根节点或者使其成为一个AVL树为止。其中也有不引入父节点指针和平衡因子bf的实现方法，比如我们可以将遍历过的节点放在一个栈当中，然后通过栈的性质找到之前的节点（这个方法我们不在这里讲解，后续如果有时间，我会专门写一篇文章来讲解这个实现方法）。

AVL树的插入

根据上面AVL树的性质，我们首先按照二叉搜索树的规则进行插入，然后让插入节点的父节点的指针指向上一个节点，更新父节点的平衡因子，如果平衡因子为0，那么就停止插入；如果平衡因子的绝对值为1，那么继续向上更新；如果平衡因子的绝对值为2，那么就特殊处理。

综上所述，我们可以将AVL树的插入分成以下几个步骤：

第一步：按照二叉搜索树的规则进行插入，链接父节点的指针

第二步：向上更新平衡因子，如果平衡因子为0就结束；如果平衡因子的绝对值为1就继续向上更新；如果平衡因子的绝对值为2就特殊处理

平衡因子更新结束的条件：更新到根节点或者平衡因子为0。

平衡因子的更新规则：

1.平衡因子=右子树高度-左子树高度

2.新增节点在父节点的左子树，父节点的平衡因子减一；新增节点在父节点的右子树，父节点的平衡因子加一

根据上述分析，我们可以写出如下代码：

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{cout << "插入值已存在，请重新输入" << endl;return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//特殊处理break;}else{assert(false);}}return true;
}

下面我们对特殊处理的情况进行分析。

我们发现，如果平衡因子的绝对值是2的时候，我们必须通过特殊处理才能保证AVL树的结构不会被破坏，那么一共有多少种特殊情况呢？我们一起来分析。

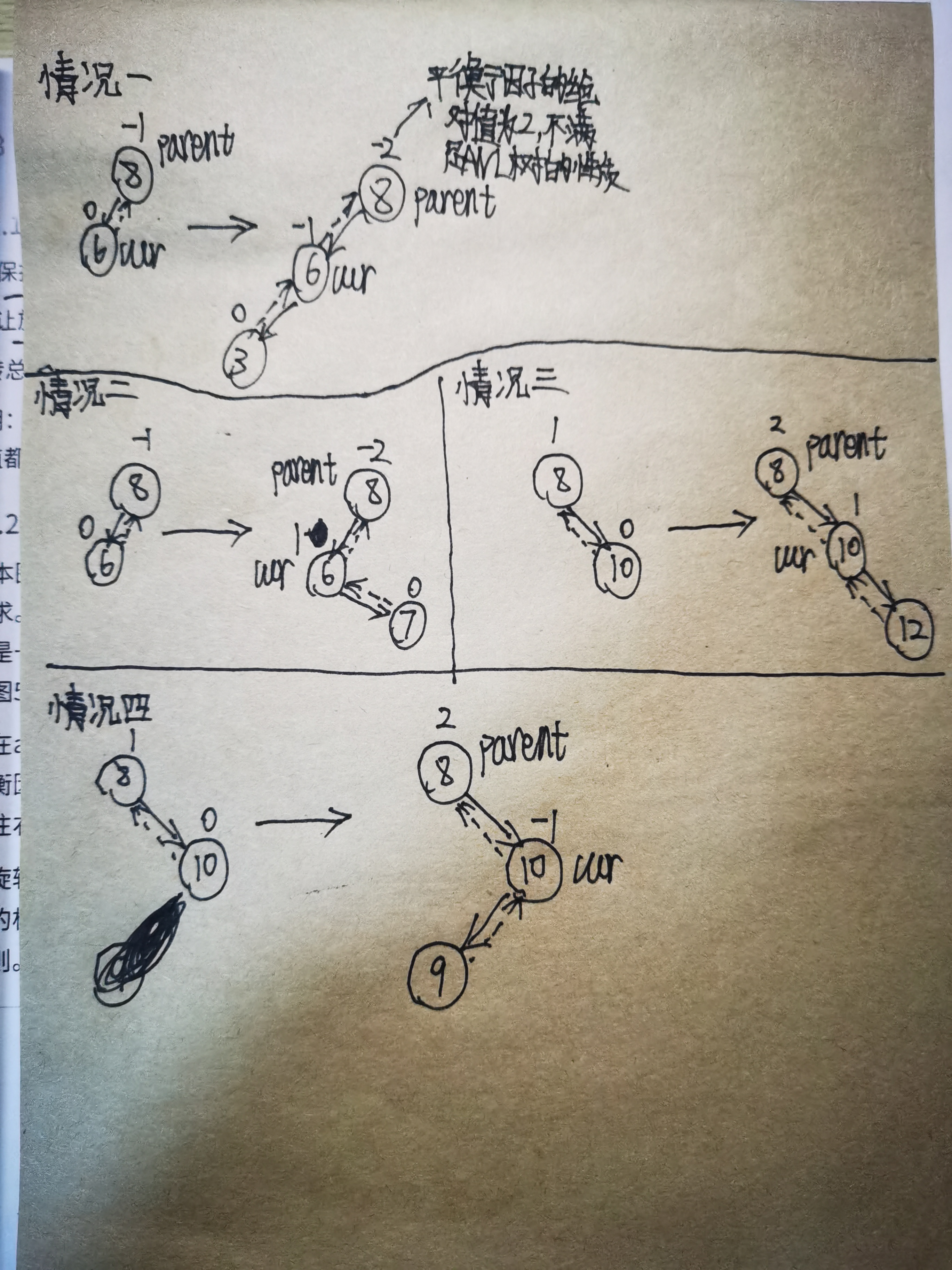
如上图所示，我们大概可以将平衡因子的绝对值为2的情况分为上述四种情况，接下来我将通过上面的四种情况来分析。

右旋转

首先我们来分析情况一：

情况一的情形是一种特殊情况，分析之后我们发现，要解决这个问题只需要让cur节点作为根节点，让parent节点作为cur的右子树，然后更新每个节点的父节点指针即可满足AVL树的性质，如下图所示：

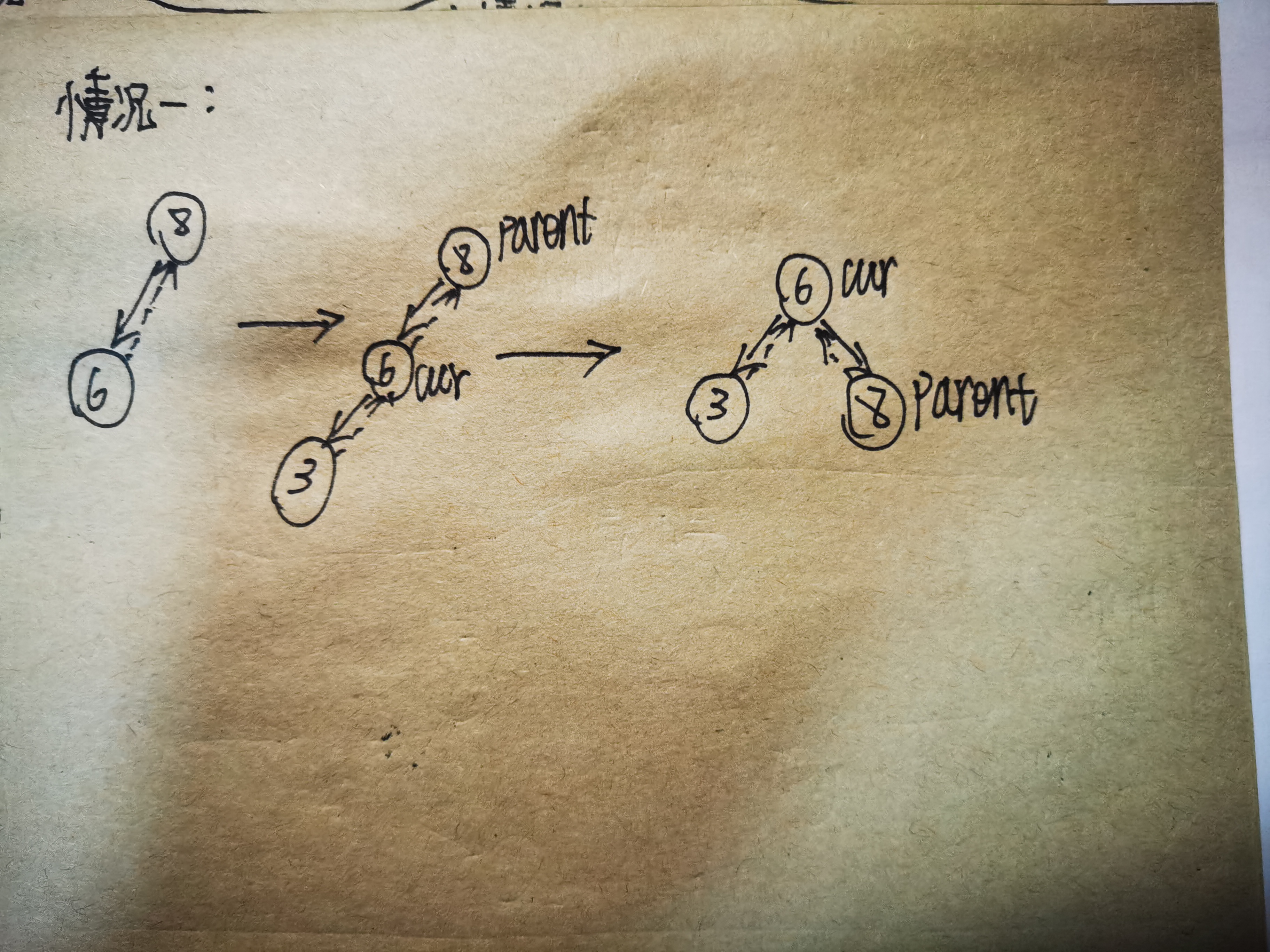
对于情况一，我们可以将其推广到一般情况，如下图所示：

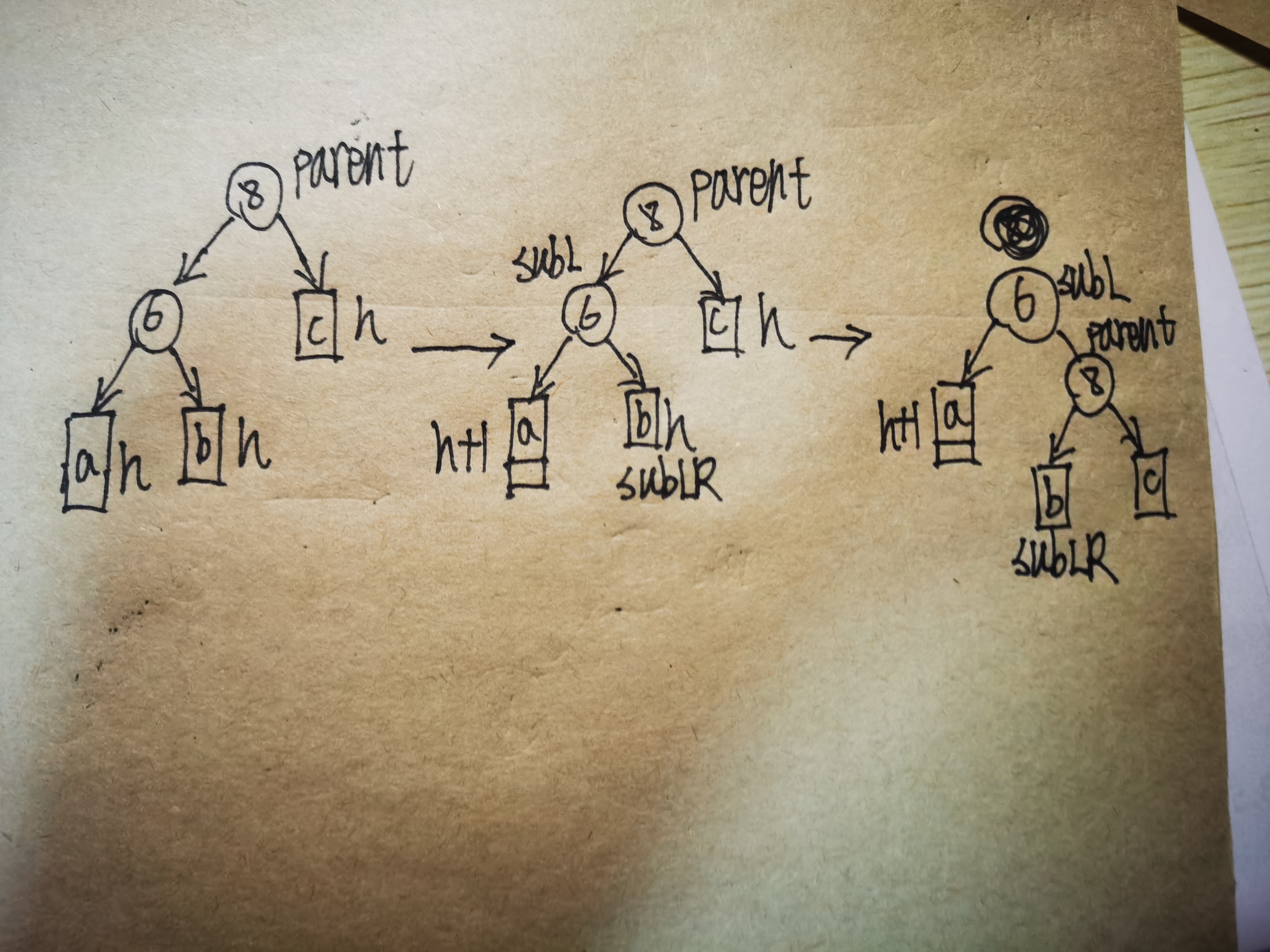 分析上述图片中的情况，我们将父节点的左节点定义为subL，subL的右节点定义为subLR，调整过后subL成为了新的根节点，parent变成了subL的右节点，subLR成为了parent的左节点。分析平衡因子，更新前parent的平衡因子为-2，subL的平衡因子为-1；更新结束后，subL和parent的平衡因子变成了0。

总结一下，我们发现，这种节点整体偏向左边，需要向右调整节点的情况我们称为右旋转，其构成的条件是：parent平衡因子为-2，且cur的平衡因子为-1，所以我们可以写下如下代码：

void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* grendParent = parent->_parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subL;}else{grendParent->_right = subL;}subL->_parent = grendParent;}subL->_bf = parent->_bf = 0;
}

分析上述代码，我们看到我们的更新步骤分下面几步：

第一步：获取subL和subLR节点，然后让parent的左指针指向subLR，让subL的右节点指针指向parent

第二步：调整父节点指针。如果subLR存在则让其父节点指针指向parent；保存grandparent指针，然后让父节点的父节点指针指向subL；

第三步：调整subL节点的根节点指针。如果parent是根节点，那么就让subL成为新的根节点；如果不是根节点，那么让grendparent相应的指针指向subL

第四步：更新subL和parent节点的平衡因子。

左旋转

我们看到情形三，我们将其推广到一般情况，如下图所示：

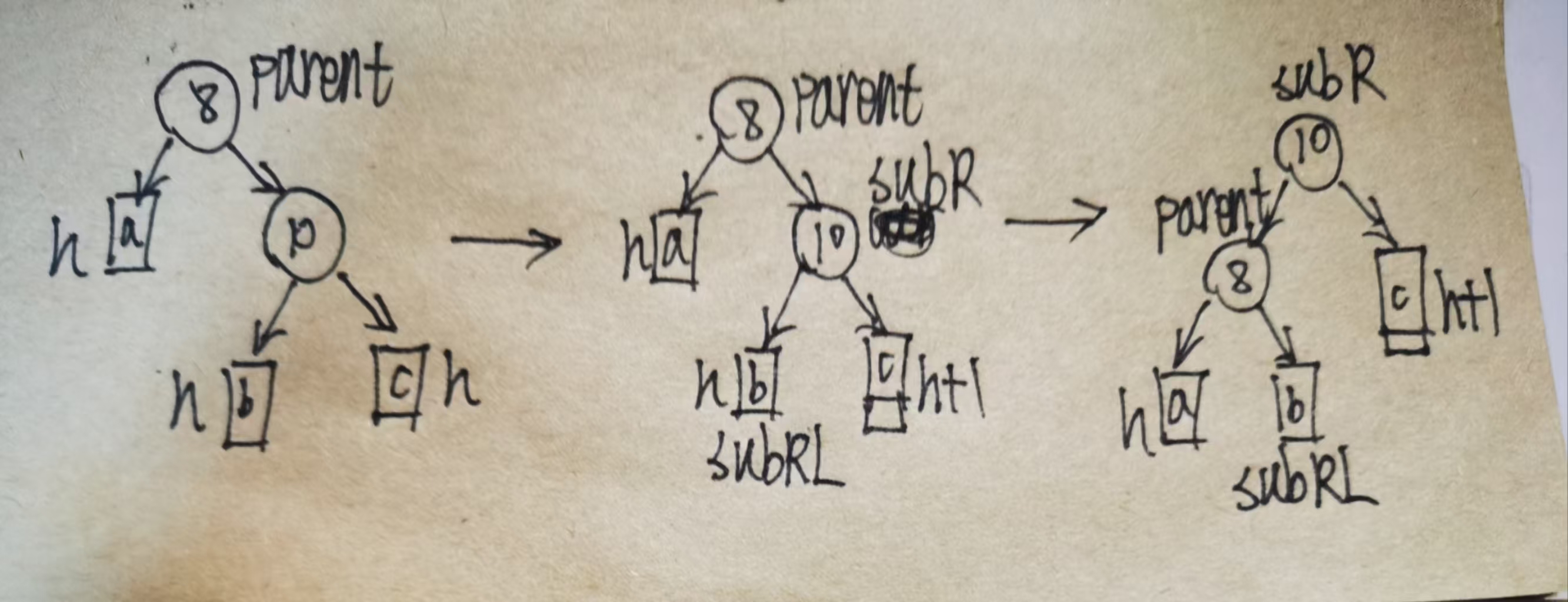
 分析上述图片中的情况，我们将父节点的右节点定义为subR，subL的左节点定义为subRL，调整过后subR成为了新的根节点，parent变成了subR的左节点，subLR成为了parent的右节点。分析平衡因子，更新前parent的平衡因子为2，subL的平衡因子为1；更新结束后，subL和parent的平衡因子变成了0。

总结一下，我们发现，这种节点整体偏向右边，需要向左调整节点的情况我们称为左旋转，其构成的条件是：parent平衡因子为2，且cur的平衡因子为1，所以我们可以写下如下代码：

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* grendParent = parent->_parent;if (subRL)subRL->_parent = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subR;}else{grendParent->_right = subR;}subR->_parent = grendParent;}parent->_bf = subR->_bf = 0;
}

分析上述代码，我们看到我们的更新步骤分下面几步：

第一步：获取subR和subRL节点，然后让parent的右指针指向subRL，让subL的左节点指针指向parent

第二步：调整父节点指针。如果subRL存在则让其父节点指针指向parent；保存grandparent指针，然后让父节点的父节点指针指向subR；

第三步：调整subL节点的根节点指针。如果parent是根节点，那么就让subR成为新的根节点；如果不是根节点，那么让grendparent相应的指针指向subR

第四步：更新subR和parent节点的平衡因子。

左右双旋

我们看到情形二，我们将其推广到一般情况，如下图所示：

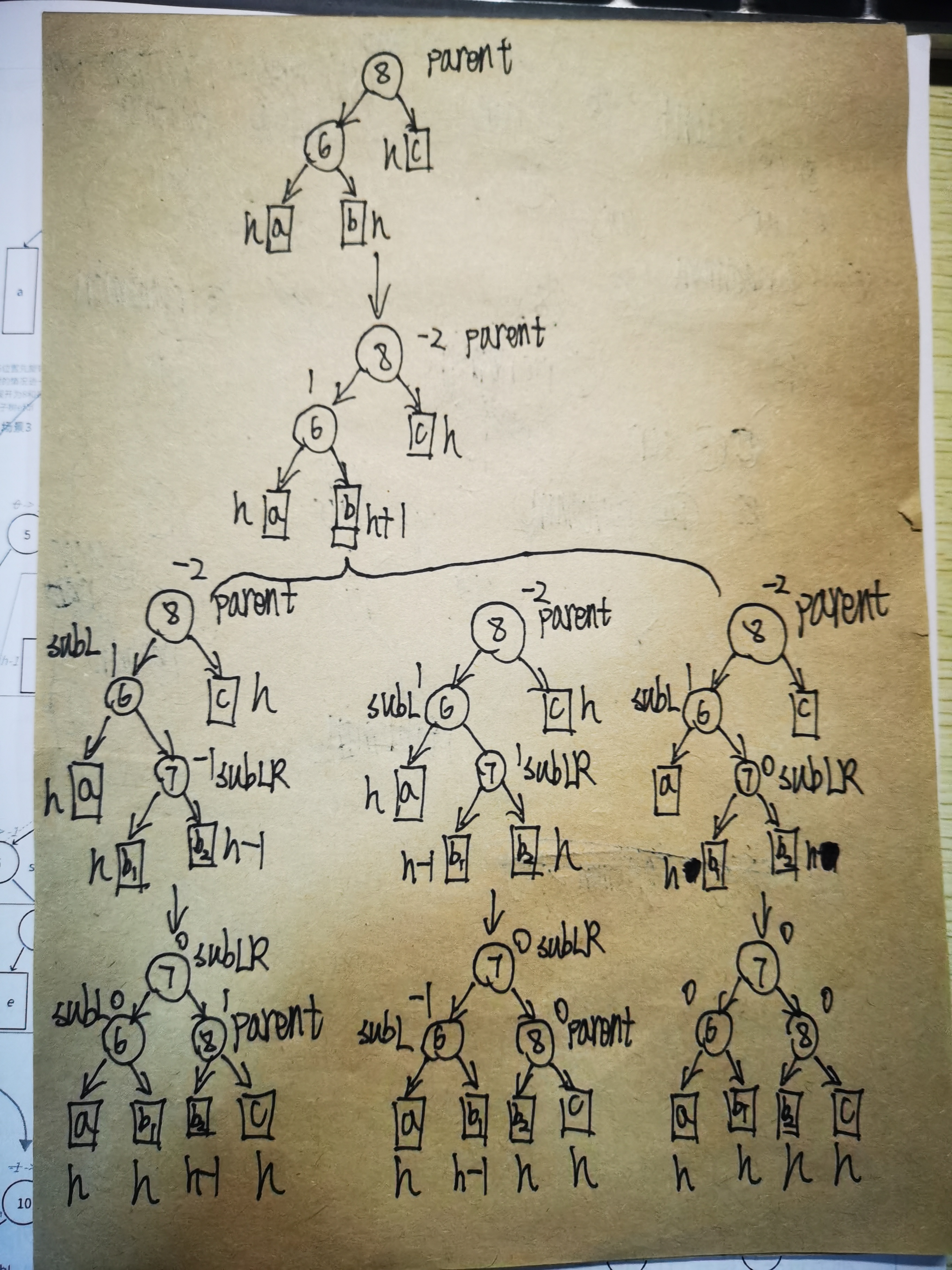
分析上述图片中的情况，我们将parent的左节点定义为subL，将subL的右节点定义为sublr，对于这个情况，我们可以根据subLR平衡因子的值将这个情形分为三种不同的情况，最终调整后的结果我们看到，subLR成为了根节点，subL成为了subLR的左节点，parent成为了subLR的右节点。

仔细观察我们发现，这种情况下的调整可以先以parent的左节点为旋转中心，进行一次左旋转，然后再以parent为旋转中心，进行一次右旋转，因此我们将这种情况称为左右双旋，满足左右双旋的条件是：parent节点的平衡因子是-2，cur节点的平衡因子是1，旋转结束后我们根据subLR节点的平衡因子的值对subLR、subL、parent的平衡因子进行赋值，因此我们可以写下如下代码：

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else{assert(false);}
}

右左双旋

我们看到情形四，我们将其推广到一般情况，如下图所示：

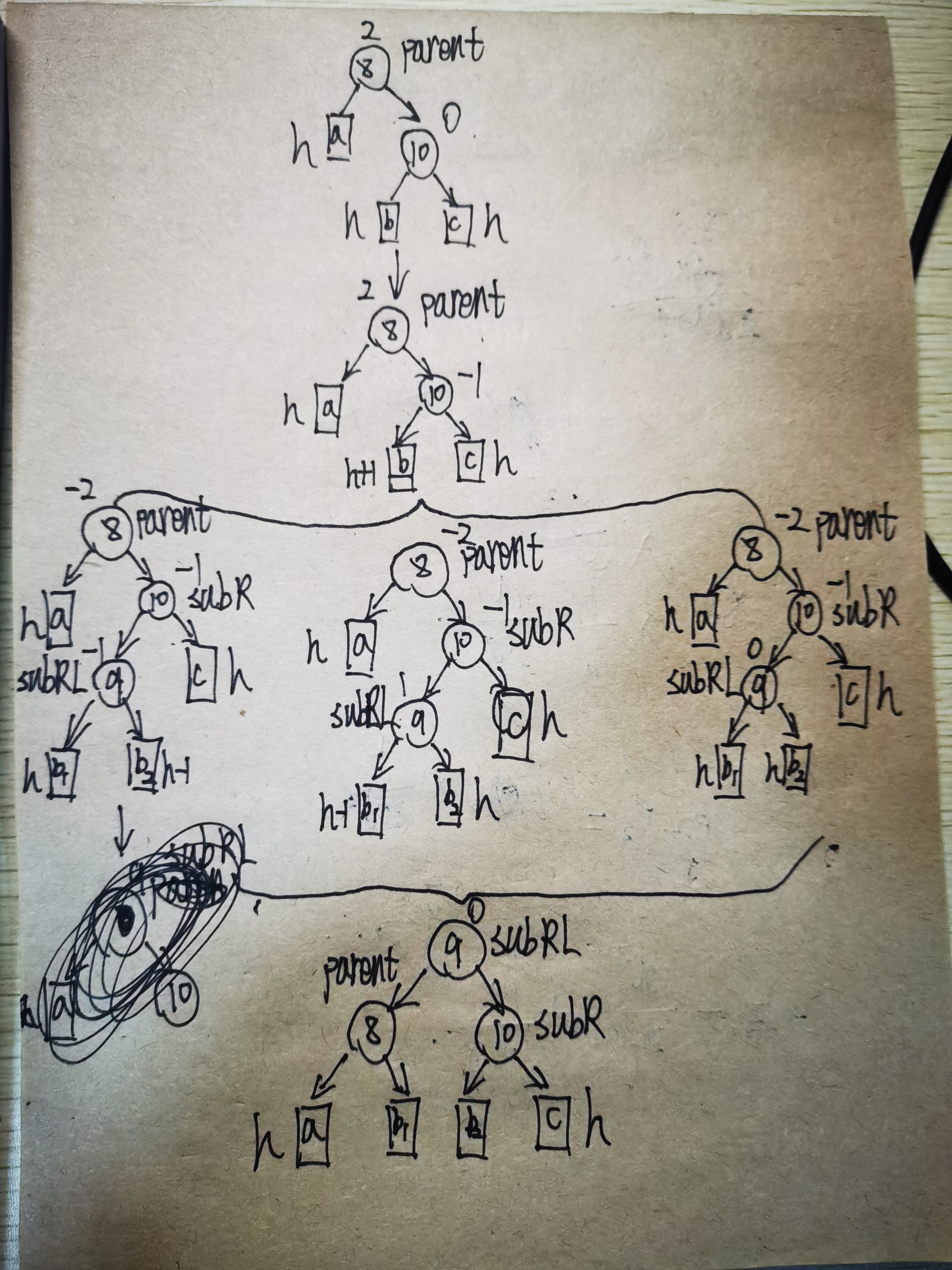
分析上述图片中的情况，我们将parent的右节点定义为subR，将subR的左节点定义为subRL，对于这个情况，我们可以根据subRL平衡因子的值将这个情形分为三种不同的情况，最终调整后的结果我们看到，subRL成为了根节点，subR成为了subRL的左节点，parent成为了subRL的右节点。

仔细观察我们发现，这种情况下的调整可以先以parent的右节点为旋转中心，进行一次右旋转，然后再以parent为旋转中心，进行一次左旋转，因此我们将这种情况称为右左双旋，满足右左双旋的条件是：parent节点的平衡因子是2，cur节点的平衡因子是-1，旋转结束后我们根据subRL节点的平衡因子的值对subRL、subR、parent的平衡因子进行赋值，因此我们可以写下如下代码：

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else if(bf==1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 1;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}
}

插入代码如下所示

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{cout << "插入值已存在，请重新输入" << endl;return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else{assert(false);}break;}else{assert(false);}}return true;
}void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* grendParent = parent->_parent;if (subRL)subRL->_parent = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subR;}else{grendParent->_right = subR;}subR->_parent = grendParent;}parent->_bf = subR->_bf = 0;
}void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* grendParent = parent->_parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subL;}else{grendParent->_right = subL;}subL->_parent = grendParent;}subL->_bf = parent->_bf = 0;
}void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else if(bf==1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 1;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}
}void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else{assert(false);}
}

AVL树的查找

AVL树的查找与二叉搜索树相同，从根节点开始查找，如果目标值大于根节点的值就走向右子树，如果目标值小于根节点的值就走向左子树，其代码如下所示：

Node* Find(const pair<K, V>& kv)
{Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){cur = cur->_left;}else if (kv.first > cur->_kv.first){cur = cur->_right;}else{return cur;}}return nullptr;
}

AVL树的遍历

我们通过中序递归的方式遍历整个AVL树，其代码如下所示：

void InOrder()
{_InOrder(_root);cout << endl;
}
private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << " ";_InOrder(root->_right);}

AVL树的节点个数以及高度

	int Height(){return _Height(_root);}int Size(){return _Size(_root);}void InOrder(){_InOrder(_root);cout << endl;}
private:int _Height(Node* root){if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}

与遍历相同，我们都是通过递归的方式遍历AVL树，不同的是它的高度是通过后序遍历完成的

判断平衡

bool _IsBalanceTree(Node* root)
{if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;if (abs(diff) >= 2){cout << root->_kv.first << "高度异常"<<endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}

AVL树代码如下所示

#include<iostream>
using namespace std;#include<assert.h>namespace FJY
{template<class K,class V>struct AVLTreeNode{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}};template<class K,class V>class AVLTree{typedef AVLTreeNode<K, V> Node;public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{cout << "插入值已存在，请重新输入" << endl;return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else{assert(false);}break;}else{assert(false);}}return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* grendParent = parent->_parent;if (subRL)subRL->_parent = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subR;}else{grendParent->_right = subR;}subR->_parent = grendParent;}parent->_bf = subR->_bf = 0;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* grendParent = parent->_parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (grendParent->_left == parent){grendParent->_left = subL;}else{grendParent->_right = subL;}subL->_parent = grendParent;}subL->_bf = parent->_bf = 0;}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subRL->_bf = 0;subR->_bf = 0;parent->_bf = 0;}else if(bf==1){subRL->_bf = 0;subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subRL->_bf = 1;subR->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else{assert(false);}}Node* Find(const pair<K, V>& kv){Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){cur = cur->_left;}else if (kv.first > cur->_kv.first){cur = cur->_right;}else{return cur;}}return nullptr;}int Height(){return _Height(_root);}int Size(){return _Size(_root);}void InOrder(){_InOrder(_root);cout << endl;}private:int _Height(Node* root){if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << " ";_InOrder(root->_right);}bool _IsBalanceTree(Node* root){if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;if (abs(diff) >= 2){cout << root->_kv.first << "高度异常"<<endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}private:Node* _root=nullptr;};
}

小结

本篇博客我们重点介绍了AVL树的插入，以及其他接口的实现，通过了解AVL树的底层实现，我们将更加深入理解平衡二叉搜索树的概念，为之后学习红黑树打下了基础，后续我们将讲解map和set的底层实现，它的底层是用的红黑树完成，所以学习AVL树将为我们后面的学习打下基础

以上就是本篇博客的主要内容，如果对您有所帮助的话，记得点赞、评论、关注加转发，您的支持就是我创作的最大动力