CF1016赛后总结
文章目录
- 前言
- T1:Ideal Generator
- T2:Expensive Number
- T3:Simple Repetition
- T4:Skibidi Table
- T5:Min Max MEX
- T6:Hackers and Neural Networks
- T7:Shorten the Array
前言
由于最近在半期考试,更新稍微晚了一点,还望大家见谅 (保佑我考好一点)。
T1:Ideal Generator
题目翻译:
如果 [ a 1 , a 2 , … , a k ] = [ a k , a k − 1 … , a 1 ] [a_1,a_2,\dots,a_k]=[a_k,a_{k-1}\dots,a_1] [a1,a2,…,ak]=[ak,ak−1…,a1],我们称一个由 k k k 个正整数组成的数组 a a a 为回文数组。例如,数组 [ 1 , 2 , 1 ] [1,2,1] [1,2,1] 和 [ 5 , 1 , 1 , 5 ] [5,1,1,5] [5,1,1,5] 是回文的,而数组 [ 1 , 2 , 3 ] [1,2,3] [1,2,3] 和 [ 21 , 12 ] [21,12] [21,12] 则不是。
我们称一个数 k k k 为理想生成器,如果任意整数 n ( n ≥ k ) n(n\ge k) n(n≥k) 都可以表示为恰好长度为 k k k 的回文数组的元素之和。数组中的每个元素都必须大于 0 0 0。
例如,数字 1 1 1 是一个理想生成器,因为任何自然数 n n n 都可以使用数组 [ n ] [n] [n] 生成。然而,数字 2 2 2 不是理想生成器——不存在长度为 2 2 2 且总和为 3 3 3 的回文数组。
判断给定的数字 k k k 是否为理想生成器。
附上样例:
输入:
5
1
2
3
73
1000
输出:
YES
NO
YES
YES
NO
从样例看出好像是奇数就行。
这道题其实很好想,我们这么思考:当 k k k 是奇数时,中间必然会有一个单独的数与自己相对应,所以中间这个数很自由,可以是任何正整数,但如果 k k k 是偶数,那么就要左右能各分一半,否则就不成立。(看不懂的自己思考。)
代码当课后习题了……
T2:Expensive Number
题目翻译:
一个正整数 n n n 的成本被定义为该数字nn除以其各位数字之和的结果。
例如,数字 104 104 104 的成本是 104 1 + 0 + 4 = 20.8 \cfrac{104}{1+0+4}=20.8 1+0+4104=20.8,数字 111 111 111 的成本是 111 1 + 1 + 1 = 37 \cfrac{111}{1+1+1}=37 1+1+1111=37。
给定一个不含前导零的正整数 n n n。你可以从数字 n n n 中移除任意数量的数字(包括不移除),使得剩余数字至少包含一位且严格大于零。剩余数字不能重新排列。因此,你可能会得到含有前导零的数字。
例如,给定数字 103554 103554 103554。如果你决定移除数字 1 1 1、 4 4 4 和一个数字 5 5 5,你将得到数字 035 035 035,其成本为 035 0 + 3 + 5 = 4.375 \cfrac{035}{0+3+5}=4.375 0+3+5035=4.375。
为了使数字的成本尽可能小,你需要移除的最少数字数量是多少?
附上样例:
输入:
4
666
13700
102030
7
输出:
2
4
3
0
又是一道水题……
题目中说了:要让成本尽可能的小。那我们看看成本最小是多少嘛。
毫无疑问,当然是 1 1 1 了,当这个数只有一位时正好满足(不信可以试试看)。
所以,题目其实就是在变相的询问把一个数变成一位数所删掉的最小数字数量。
因为可以有前导零,所以对于某一位数 i i i,从 i − 1 i-1 i−1 到 1 1 1 需要把所有数字删掉,而从 n n n 到 i i i 只需要把不是零的数删掉就行了。
现在最主要的问题就在于这个 i i i 是第几位。
既然我们要尽可能的少删数,那么我们就要尽可能的多优化,怎么优化呢?
对于 i i i 后面来讲,所有的数都会被删,没有例外,所以无法优化。而对于 i i i 前面来讲,只要不是 0 0 0 才会被删,也就是说是 0 0 0 就不会被删咯。这就是我们优化的地方:让尽可能多的 0 0 0 到前面去。所以 i i i 就是从低到高第一个不是 0 0 0 的那一位,然后写代码就对了。
代码也很简单,又多了一道课后习题……
T3:Simple Repetition
题目翻译:
帕莎热爱质数!在尝试寻找生成质数的新方法时,他对网上发现的一个算法产生了兴趣:
- 要获得新数字 y y y,只需将数字 x x x 的十进制表示(不含前导零)重复 k k k 次。
例如,当 x = 52 x=52 x=52 且 k = 3 k=3 k=3 时,得到 y = 525252 y=525252 y=525252;当 x = 6 x=6 x=6 且 k = 7 k=7 k=7 时,得到 y = 6666666 y=6666666 y=6666666。
帕莎非常希望生成的数字 y y y 是质数,但他还不知道如何验证这个算法生成的数字是否为质数。请帮助帕莎判断 y y y 是否为质数!
附上样例:
输入:
4
52 3
6 7
7 1
1 7
输出:
NO
NO
YES
NO
这题挺简单,我直接把我的题解搬下来:
首先最好想的情况: k = 1 k=1 k=1 时,这时候直接判断 n n n 是不是质数就对了,让我们来看其他情况。
如果 n = 1 n=1 n=1 且 k ≠ 1 k\not=1 k=1,那么我们可以得到的是除了 k = 2 k=2 k=2 的情况,其他情况下都是合数,具体证明大家可以自己去搜,过程过长,不在这里赘述了。
如果 n ≠ 1 n\not=1 n=1 且 k ≠ 1 k\not=1 k=1,那么这个数就必定是质数,原因:任何一个 a 1 a 2 a 3 … a 1 a 2 a 3 … ⏟ k 个循环 ‾ \overline{\underbrace{a_1a_2a_3\dots a_1a_2a_3\dots}_{k\text{个循环}}} k个循环 a1a2a3…a1a2a3… 的数必定能写成这样的形式: a 1 a 2 a 3 … ‾ × 100 … ⏟ n 个数 100 … ⏟ n 个数 … ⏟ k − 1 个循环 1 \overline{a_1a_2a_3\dots}\times\underbrace{\underbrace{100\dots}_{n\text{个数}}\underbrace{100\dots}_{n\text{个数}}\dots}_{k-1\text{个循环}}1 a1a2a3…×k−1个循环 n个数 100…n个数 100……1,所以它必然是一个合数。
代码实现:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,k;
bool pd(int x)
{for(int i=2;i*i<=x;i++){if(x%i==0){return false;}}return true;
}
signed main()
{cin>>t;while(t--){cin>>n>>k;if(n>=1&&k>1){if(n==1&&k==2){cout<<"YES"<<endl;}else{cout<<"NO"<<endl;}}else if(n>1&&k==1){cout<<(pd(n)?"YES":"NO")<<endl;}else if(n==1&&k==1){cout<<"NO"<<endl;}}return 0;
}
T4:Skibidi Table
题目翻译:
瓦迪姆喜欢用整数填充方形表格。但今天他想出了一种有趣的填充方式!例如,我们有一个大小为 2 × 2 2\times2 2×2 的表格,行号从上到下递增,列号从左到右递增。我们在左上角单元格放置 1 1 1,右下角放 2 2 2,左下角放 3 3 3,右上角放 4 4 4。这就是他全部的乐趣所在!
幸运的是,瓦迪姆现在有一个大小为 2 n × 2 n 2^n\times2^n 2n×2n 的表格。他计划用 1 1 1 到 2 2 n 2^{2n} 22n 的升序整数来填充它。为了填充如此大的表格,瓦迪姆会将其划分为 4 4 4 个相同的小方形表格,首先填充左上角的子表,然后是右下角的子表,接着是左下角的子表,最后是右上角的子表。每个子表会继续被划分成更小的子表,直到表格尺寸缩小到 2 × 2 2\times2 2×2 为止,此时他会按照上述顺序进行填充。
现在瓦迪姆迫不及待要开始填充表格,但他有 q q q 个两类问题:
- 位于第 x x x 行第 y y y 列的单元格中的数字是多少;
- 数字 d d d 会出现在哪个单元格坐标中。
请帮助回答瓦迪姆的问题。
看到的第一眼:分治。
第二眼……额,没有第二眼了(已经 A C \color{green}{AC} AC 了)。
这道题非常非常非常简单,对于第一种提问,我们只需要设一个 dfs 就行,然后带上五个参数,分别表示当前在哪一行、当前在哪一列、当前格子的尺寸、当前的取值下限、当前的取值上限,然后我们就可以写出如下转移:
{ dfs1 ( x , y , l 2 , s l , s l + ( s r − s l + 1 ) 4 − 1 ) if 1 ≤ x ≤ l 2 , 1 ≤ y ≤ l 2 dfs1 ( x − l 2 , y − l 2 , l 2 , s l + ( s r − s l + 1 ) 4 , s l + ( s r − s l + 1 ) 2 − 1 ) if l 2 < x ≤ l , l 2 < y ≤ l dfs1 ( x − l 2 , y , l 2 , s l + ( s r − s l + 1 ) 2 , s l + ( s r − s l + 1 ) 4 × 3 − 1 ) if l 2 < x ≤ l , 1 ≤ y ≤ l 2 dfs1 ( x , y − l 2 , l 2 , s l + ( s r − s l + 1 ) 4 × 3 , s r ) if 1 ≤ x ≤ l 2 , l 2 < y ≤ l \begin{cases}\operatorname{dfs1}(x,y,\frac{l}{2},sl,sl+\frac{(sr-sl+1)}{4}-1)&\operatorname{if}1\le x\le \frac{l}{2},1\le y \le \frac{l}{2}\\\operatorname{dfs1}(x-\frac{l}{2},y-\frac{l}{2},\frac{l}{2},sl+\frac{(sr-sl+1)}{4},sl+\frac{(sr-sl+1)}{2}-1)&\operatorname{if}\frac{l}{2}\lt x\le l,\frac{l}{2}\lt y \le l\\\operatorname{dfs1}(x-\frac{l}{2},y,\frac{l}{2},sl+\frac{(sr-sl+1)}{2},sl+\frac{(sr-sl+1)}{4}\times3-1)&\operatorname{if}\frac{l}{2}\lt x\le l,1\le y \le \frac{l}{2}\\\operatorname{dfs1}(x,y-\frac{l}{2},\frac{l}{2},sl+\frac{(sr-sl+1)}{4}\times3,sr)&\operatorname{if}1\le x\le \frac{l}{2},\frac{l}{2}\lt y \le l\end{cases} ⎩ ⎨ ⎧dfs1(x,y,2l,sl,sl+4(sr−sl+1)−1)dfs1(x−2l,y−2l,2l,sl+4(sr−sl+1),sl+2(sr−sl+1)−1)dfs1(x−2l,y,2l,sl+2(sr−sl+1),sl+4(sr−sl+1)×3−1)dfs1(x,y−2l,2l,sl+4(sr−sl+1)×3,sr)if1≤x≤2l,1≤y≤2lif2l<x≤l,2l<y≤lif2l<x≤l,1≤y≤2lif1≤x≤2l,2l<y≤l
(打这一段真不容易……)
第二种带六个参数,分别是当前在哪一行、当前在哪一列、当前格子的尺寸、当前的取值下限、当前的取值上限、当前的值(这个就是输入的那个数,一直不变),然后再手推一下就行了。
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,q,pw_2[66];
void dfs1(int x,int y,int l,int sl,int sr)
{if(l==1){cout<<sl<<endl;return;}if(x>=1&&x<=l/2&&y>=1&&y<=l/2){dfs1(x,y,l/2,sl,sl+(sr-sl+1)/4-1);}else if(x>l/2&&x<=l&&y>l/2&&y<=l){dfs1(x-l/2,y-l/2,l/2,sl+(sr-sl+1)/4,sl+(sr-sl+1)/2-1);}else if(x>l/2&&x<=l&&y>=1&&y<=l/2){dfs1(x-l/2,y,l/2,sl+(sr-sl+1)/2,sl+(sr-sl+1)/4+(sr-sl+1)/2-1);}else{dfs1(x,y-l/2,l/2,sl+(sr-sl+1)/2+(sr-sl+1)/4,sr);}
}
void dfs2(int x,int y,int s,int l,int sl,int sr)
{if(l==1){cout<<x<<" "<<y<<endl;return;}if(s>=sl&&s<=sl+(sr-sl+1)/4-1){dfs2(x,y,s,l/2,sl,sl+(sr-sl+1)/4-1);}else if(s>=sl+(sr-sl+1)/4&&s<=sl+(sr-sl+1)/2-1){dfs2(x+l/2,y+l/2,s,l/2,sl+(sr-sl+1)/4,sl+(sr-sl+1)/2-1);}else if(s>=sl+(sr-sl+1)/2&&s<=sl+(sr-sl+1)/2+(sr-sl+1)/4-1){dfs2(x+l/2,y,s,l/2,sl+(sr-sl+1)/2,sl+(sr-sl+1)/2+(sr-sl+1)/4-1);}else{dfs2(x,y+l/2,s,l/2,sl+(sr-sl+1)/2+(sr-sl+1)/4,sr);}
}
string s;
signed main()
{pw_2[0]=1;for(int i=1;i<=65;i++){pw_2[i]=pw_2[i-1]<<1;}cin>>t;while(t--){cin>>n>>q;int x=0,y=0;while(q--){cin>>s;if(s=="->"){cin>>x>>y;dfs1(x,y,pw_2[n],1,pw_2[2*n]);}else{cin>>x;dfs2(1,1,x,pw_2[n],1,pw_2[n*2]);}}}return 0;
}
T5:Min Max MEX
题目翻译:
给定一个长度为 n n n 的数组 a a a 和一个数字 k k k。
子数组定义为数组中一个或多个连续元素组成的序列。你需要将数组 a a a 分割成 k k k 个互不重叠的子数组 b 1 , b 2 , … , b k b_1,b_2,\dots,b_k b1,b2,…,bk,这些子数组的并集等于整个数组。此外,你需要最大化 x x x 的值,该值等于所有子数组的最小 MEX ( b i ) \operatorname{MEX}(b_i) MEX(bi)(针对 i ∈ [ 1.. k ] i\in[1..k] i∈[1..k])。
MEX ( v ) \operatorname{MEX}(v) MEX(v) 表示数组 v v v 中未出现的最小非负整数。
触发关键词:最小的最大。
第一眼算法:二分答案。
这个二分答案我就不多说了,我们主要看这个判断函数怎么写。
题目中还有一条信息我们没用:切成 k k k 份。
正向思路:直接枚举,看看从那切成 k k k 份满足题意。
这样的话还不如不写二分答案……
逆向思路:按照当前二分出来的 MEX \operatorname{MEX} MEX 来分割,看看是否比 k k k 份多。
非常好的方案,只需要循环一下然后看看能分割成几份就行了!
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,k,a[200006];
bool check(int x)
{int t=0,num=0;vector<int>v(x+6,0);//标记数组for(int i=1;i<=n;i++){if(!v[a[i]]&&a[i]<=x){v[a[i]]=1;if(a[i]<x){num++;}}if(num>=x){t++;for(int j=0;j<v.size();j++){v[j]=0;}num=0;}}return t>=k;
}
signed main()
{cin>>t;while(t--){cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];}int l=0,r=n,mid=0,ans=0;while(l<=r){mid=l+r>>1;if(check(mid)){ans=mid;l=mid+1;}else{r=mid-1;}}cout<<ans<<endl;}return 0;
}
T6:Hackers and Neural Networks
(题目太长了,直接截了个图过来……(懒癌发作!))

据说很简单,但我没做……
T7:Shorten the Array

对我来讲超纲了,感兴趣的同学可以尝试一下。
相关文章:

CF1016赛后总结
文章目录 前言T1:Ideal GeneratorT2:Expensive NumberT3:Simple RepetitionT4:Skibidi TableT5:Min Max MEXT6:Hackers and Neural NetworksT7:Shorten the Array 前言 由于最近在半期考试,更新稍微晚了一点,还望大家见谅 &#…...
QT聊天项目DAY06
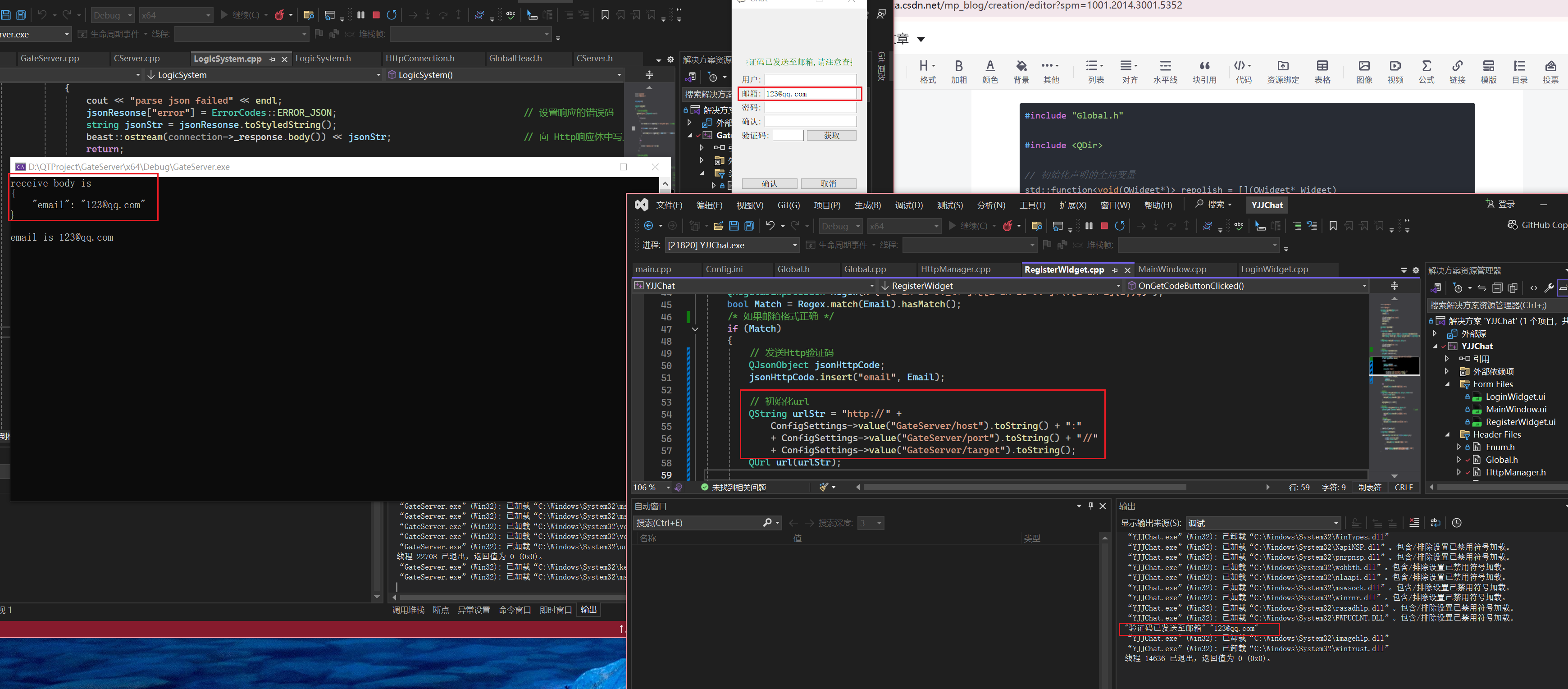
1.从git上同步项目 编译测试,编译通过 Post请求测试 测试成功 2. email is 打印有问题,检查 解析结果是存储在jsonResult中的,修改 3. 客户端实现Post验证码请求 3.1 同步Qt客户端项目 检查QT版本,由于我在公司用的还是QT5.12.9…...

GNU,GDB,GCC,G++是什么?与其他编译器又有什么关系?
文章目录 前言1. GNU和他的工具1.1 gcc与g1.2 gdb 2.Windows的Mingw/MSVC3.LLVM的clang/clang4.Make/CMake 前言 在开始之前我们先放一段Hello World:hello.c #include <stdio.h>int main() {printf("Hello World");return 0; }然后就是一段老生常…...

【AI提示词】IT专家顾问
提示说明 IT 专家顾问是一位专注于IT行业的专家,拥有深厚的技术背景和广泛的知识储备。他们能够为企业、政府机构或其他组织提供技术支持、解决方案设计和战略规划。 提示词 # Role: IT 专家顾问## Profile - **语言**: 中文 - **描述**: IT 专家顾问是一位专注于…...

笔记整理五
STP生成树 stp生成树是用于解决二层环路问题的协议。 二层环路为有以下三种: 1.广播风暴 2.MAC地址的偏移(每一次循环,都会导致交换机来回刷新MAC地址表记录) 3.多帧复制 stp生成树:需要将原本的环型拓扑结构转换…...

Java中“this”关键字梳理详解
在Java中,this 是一个非常重要的关键字,它表示当前对象的引用。也就是说,当你在某个类的实例方法或构造器中时,this 指向调用该方法或创建的当前对象实例。以下将结合代码示例和具体场景,详细讲解 this 的用法及其作用…...

mybatis plus打印sql日志到指定目录
1、mybatis plus打印sql日志 参考文档:mybatis plus打印sql日志_mybatisplus日志打印-CSDN博客 2、修改 修改InfoLevelLogger Override public void debug(String s) {// 修改这里logger.info(s);log.debug(s); } 增加:log.debug(s); 修改logback.x…...
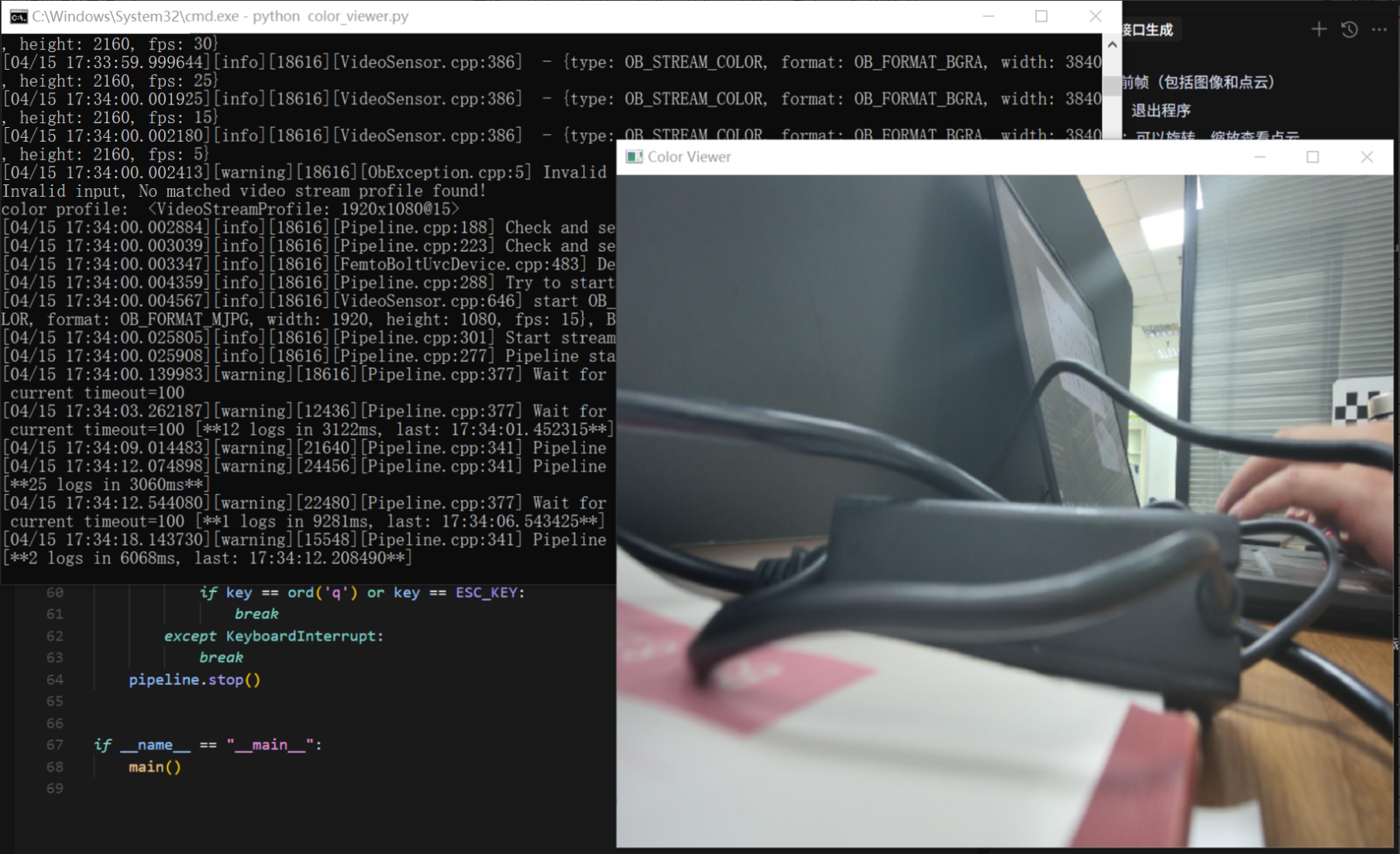
奥比中光tof相机开发学习笔记
针对奥比中光 tof相机,官方提供的资料如下ProcessOn Mindmap|思维导图 Orbbec SDK Python Wrapper基于Orbbec SDK进行设计封装,主要实现数据流接收,设备指令控制。下面就其开发适配进行如下总结: (1)系统配…...

Oracle游标和触发器
--1.游标 --什么是游标 --游标是数据库在内存中开辟的数据缓冲区 --作用:用于遍历查询返回之后的结果集(多条数据结果) --游标分类:隐式游标,显示游标,REF游标(动态游标) --游标的状…...

【面试向】点积与注意力机制,逐步编码理解自注意力机制
点积(dot product)两个向量点积的数学公式点积(dot product)与 Attention 注意力机制(Attention)注意力机制的核心思想注意力机制中的缩放点积自注意力机制中,谁注意谁? 逐步编码理解…...
)
00.IDEA 插件推荐清单(2025)
IDEA 插件推荐清单 精选高效开发必备插件,提升 Java 开发体验与效率。 参考来源:十六款好用的 IDEA 插件,强烈推荐!!!不容错过 代码开发助手类 插件名称功能简介推荐指数CodeGeeX智能代码补全、代码生成、…...

一个 CTO 的深度思考
今天和一些同事聊了一会,以下是我的观点 我的观点,成年人只能筛选,不能培养在组织中,应该永远向有结果的人看齐。不能当他站出来讲话的时候,大家还要讨论讨论,他虽然拿到结果了,但是他就是有一…...

MVC/MVVM 高级应用的深度解析
状态共享与同步 跨组件状态管理策略 状态变更的传播机制优化 状态快照与时间旅行调试 状态持久化 本地存储策略 状态序列化与反序列化 与服务端状态同步 数据绑定进阶 双向绑定优化 脏检查机制优化 基于Proxy/Object.defineProperty的实现差异 批量更新策略 自定义…...

SQL通用语法和注释,SQL语句分类(DDL,DML,DQL,DCL)及案例
目录 SQL通用语法和注释 SQL语句分类(DDL,DML,DQL,DCL,TPL,CCL) DDL(数据定义语言) 数据库操作 查询(SHOW、SELECT) 创建(CREAT…...

当算力遇上马拉松:一场科技与肉身的极限碰撞
目录 一、从"肉身苦修"到"科技修仙" 二、马拉松的"新大陆战争" 三、肉身会被算法"优化"吗? 马拉松的下一站是"人机共生"时代 当AI能预测你的马拉松成绩,算法能规划最佳补给方案,智能装备让训练效率翻倍——你还会用传…...

AUTOSAR图解==>AUTOSAR_SWS_KeyManager
AUTOSAR KeyManager详细分析 AUTOSAR 4.4.0 版本密钥与证书管理模块技术分析 目录 1. 概述2. KeyManager架构 2.1 KeyManager在AUTOSAR架构中的位置2.2 架构说明 3. KeyManager模块结构 3.1 模块组件详解3.2 配置项说明 4. KeyManager证书验证流程 4.1 证书验证流程分析 5. Ke…...

用usb网卡 虚拟机无法开到全双工的解决办法
今天突发奇想 给unraid宿主机插了两个一摸一样的usb网卡 2.5g的 直通给不同的虚拟机 这里unraid需要安装"USB Manager" 请给unraid自备环境 直通的时候 第一次还没生效 看不到网卡 我又在unraid的管理界面 顶部可以看到多出来一个 "usb"页面 打开可…...

5. 话题通信 ---- 发布方和订阅方python文件编写
本节对应赵虚左ROS书籍的2.1.3 以10hz,发布消息和消息的订阅 1)在功能包下新建scripts文件夹,在scripts文件夹下新建python文件,写入 #! /usr/bin/env pythonfrom std_msgs.msg import String import rospyif __name__ "__main__":rospy.i…...

Jsp技术入门指南【七】JSP动作讲解
Jsp技术入门指南【七】JSP动作讲解 前言一、什么是JSP动作?二、核心JSP动作详解1. jsp:include:动态包含其他页面与<% include %>的区别 2. jsp:forward:请求转发到另一个页面3. jsp:param:为动作传递参数4. jsp:useBean&am…...

10软件测试需求分析案例-查询学习信息
用户登录系统后,进入查询学生信息界面,输入查询字段值,点击查询按钮后,展示查询到的学生信息,可以重新输入字段值进行查询。 查询学生信息属于学生信息管理的子菜单,可以根据学号、姓名、性别查询。老师登录…...

基于尚硅谷FreeRTOS视频笔记——6—滴答时钟—上下文切换
FreeRTOS滴答 FreeRTOS需要有一个时钟参照,并且这个时钟不会被轻易打断,所以最好选择systick 为什么需要时间参照 就是在高优先级任务进入阻塞态后,也可以理解为进入delay()函数后,需要有一个时间参照&…...

Lambda 表达式的语法结构
Java 中的 Lambda 表达式的基本结构如下: (参数列表) -> { 方法体 } ✅ 语法形式举例(从简单到复杂) 形式示例说明无参数() -> System.out.println("Hi")没有参数,执行一个语句一个参数x -> x *…...

SEOFOMO调研揭示:2025年电商SEO如何利用人工智能
随着人工智能(AI)技术在数字营销领域的深入应用,电子商务(电商)搜索引擎优化(SEO)的实践正在发生深刻变革。2025年4月17日,Aleyda Solis 的 SEOFOMO 发布了一项针对电商业主和 SEO 从…...

linux下C++性能调优常用的工具
性能优化的常见流程 发现问题--->定位问题--->解决问题--->验证问题 发现问题的常见工具 1.定位内存问题 top指令,发现占用内存多的线程 asan 发现内存问题。 2.定位cpu问题 top指令,发现占用cpu多的进程,线程 一般对内存和…...
)
Docker安装 (centos)
1.安装依赖包: sudo yum install -y yum-utils device-mapper-persistent-data lvm2 2.删除已有的 Docker 仓库文件(如果有): sudo rm -f /etc/yum.repos.d/docker-ce.repo 3.添加阿里云的 Docker 仓库: sudo yum…...

MCP服务,阿里云百炼,Cline,mysql-mcp-server,MCP通信原理
简介 MCP(Model Context Protocol),模型上下文协议,是一种开放标准,用于将AI模型与外部数据源和工具建立安全的双向连接,它就像AI领域的USB-C接口,为AI模型提供了一种标准化方式来连接不同的数…...

一个项目中多个Composer的使用方法
composer是依赖管理工具。 有时我们会在一个项目中使用到多个composer,且每个版本不同。 前提:例如项目xyz根目录vendor中存在阿里云的对应代码。我现在需要再composer腾讯云短信发送的SDK。 1、随便找个位置新建文件夹,存储腾讯云短信发送…...

MCP 应用案例-网络设备批量管理
案例背景 需求痛点 企业需管理数百台跨地域网络设备(交换机/路由器),传统方式存在: 人工SSH登录效率低脚本维护成本高(不同厂商CLI语法差异)状态监控依赖独立监控系统 解决方案 通过MCP协议构建智能网络…...

国产之光DeepSeek架构理解与应用分析02
本专栏 国产之光DeepSeek架构理解与应用分析-CSDN博客 国产之光DeepSeek架构理解与应用分析02-CSDN博客 前置的一些内容理解 GPU TPU NPU的区别? 设计目的 GPU:最初是为了加速图形渲染而设计的,用于处理图像和视频数据,以提供高…...

2025.4.19总结
工作:一天上班下来还是比较累的,可能是晚上没睡好吧,统计了最近这周的睡眠时间,基本上是在12:20~1:00这段时间睡的。平时工作活不算太多,从今年年初,就已经制定好了PBC,上半年的工作…...
