【java实现+4种变体完整例子】排序算法中【希尔排序】的详细解析,包含基础实现、常见变体的完整代码示例,以及各变体的对比表格
以下是希尔排序的详细解析,包含基础实现、常见变体的完整代码示例,以及各变体的对比表格:

一、希尔排序基础实现
原理
希尔排序是插入排序的改进版本,通过分步缩小增量间隔,将数组分成多个子序列进行插入排序,逐步减少元素移动次数。
代码示例
public class ShellSort {void sort(int[] arr) {int n = arr.length;// 初始增量(希尔原始增量:n/2,每次除以2)for (int gap = n / 2; gap > 0; gap /= 2) {// 对每个子序列进行插入排序for (int i = gap; i < n; i++) {int temp = arr[i];int j;// 插入排序,步长为gapfor (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}}}
}
复杂度分析
- 时间复杂度:
- 平均:
O(n^(3/2))(希尔原始增量)。 - 最坏:
O(n²)(依赖增量序列)。 - 最好:
O(n log n)。
- 平均:
- 空间复杂度:
O(1)。 - 稳定性:不稳定(相同值的元素可能因交换顺序改变相对位置)。
二、常见变体及代码示例
1. Hibbard增量序列
改进点:增量序列选择 2^k - 1(如1、3、7、15…),减少子序列间的相关性。
适用场景:平均性能优于原始希尔增量。
public class HibbardShellSort {void sort(int[] arr) {int n = arr.length;// 生成Hibbard增量序列int gap = 1;while (gap < n / 2) {gap = 2 * gap + 1;}while (gap >= 1) {for (int i = gap; i < n; i++) {int temp = arr[i];int j;for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}gap = (gap - 1) / 2; // 逆序应用增量}}
}
2. Sedgewick增量序列
改进点:增量序列按特定公式生成(如1, 5, 19, 41, 109…),优化时间复杂度。
适用场景:理论时间复杂度更低(接近 O(n^(4/3)))。
public class SedgewickShellSort {void sort(int[] arr) {int n = arr.length;// 生成Sedgewick增量序列List<Integer> gaps = new ArrayList<>();for (int h = 1; h < n; ) {gaps.add(h);if (h <= n / 3) h = 3 * h + 1;else h = 3 * (h / 2) + 1;}// 逆序应用增量for (int i = gaps.size() - 1; i >= 0; i--) {int gap = gaps.get(i);for (int j = gap; j < n; j++) {int temp = arr[j];int k;for (k = j; k >= gap && arr[k - gap] > temp; k -= gap) {arr[k] = arr[k - gap];}arr[k] = temp;}}}
}
3. 斐波那契增量序列
改进点:增量序列基于斐波那契数列(如1、1、2、3、5…),减少子序列相关性。
适用场景:理论上的优化尝试。
public class FibonacciShellSort {void sort(int[] arr) {int n = arr.length;// 生成斐波那契增量序列List<Integer> gaps = new ArrayList<>();int a = 0, b = 1;while (b < n) {gaps.add(b);int temp = a + b;a = b;b = temp;}// 逆序应用增量for (int i = gaps.size() - 1; i >= 0; i--) {int gap = gaps.get(i);for (int j = gap; j < n; j++) {int temp = arr[j];int k;for (k = j; k >= gap && arr[k - gap] > temp; k -= gap) {arr[k] = arr[k - gap];}arr[k] = temp;}}}
}
三、变体对比表格
| 变体名称 | 增量序列 | 时间复杂度 | 空间复杂度 | 稳定性 | 主要特点 | 适用场景 |
|---|---|---|---|---|---|---|
| 基础希尔排序(原始增量) | n/2, n/4, ..., 1 | O(n^(3/2))(平均)O(n²)(最坏) | O(1) | 不稳定 | 简单易实现,但性能依赖增量选择 | 通用场景,增量选择简单 |
| Hibbard增量序列 | 2^k -1(如1,3,7,15…) | O(n^(3/2))(平均) | O(1) | 不稳定 | 减少子序列相关性,性能更优 | 需要平衡性能与实现复杂度的场景 |
| Sedgewick增量序列 | 1,5,19,41,… | O(n^(4/3))(理论最优) | O(1) | 不稳定 | 理论时间复杂度最低,适合大数据 | 需要极致性能的场景 |
| 斐波那契增量序列 | 斐波那契数列(如1,2,3…) | O(n^(3/2))(平均) | O(1) | 不稳定 | 理论上的优化尝试,实际效果需验证 | 研究或特定实验场景 |
四、关键选择原则
- 基础场景:优先使用基础希尔排序(原始增量),因其简单且性能足够。
- 性能优化:
- Hibbard增量:适合需要比原始增量更好的平均性能,且实现复杂度较低。
- Sedgewick增量:适用于大数据场景,理论时间复杂度最低。
- 增量序列选择:
- 理论最优:Sedgewick增量。
- 实现简单:Hibbard增量。
- 稳定性需求:所有变体均不稳定,若需稳定排序需选择其他算法(如归并排序)。
- 实验场景:斐波那契增量可用于探索不同增量序列的效果,但实际应用较少。
通过选择合适的增量序列,可在特定场景下显著提升希尔排序的效率。例如,Sedgewick增量在理论上的时间复杂度最低,适合大数据排序;而Hibbard增量则在实现复杂度与性能之间取得平衡。
相关文章:

【java实现+4种变体完整例子】排序算法中【希尔排序】的详细解析,包含基础实现、常见变体的完整代码示例,以及各变体的对比表格
以下是希尔排序的详细解析,包含基础实现、常见变体的完整代码示例,以及各变体的对比表格: 一、希尔排序基础实现 原理 希尔排序是插入排序的改进版本,通过分步缩小增量间隔,将数组分成多个子序列进行插入排序&#…...

回车键监听
全局添加回车监听 // 定义一个具名函数function globalEnterHandler(event) {if (event.key Enter) {$scope.getsearch();}}// 添加监听document.addEventListener(keydown, globalEnterHandler);// 需要移除的时候,调用这个document.addEventListener(keydown, gl…...

matlab 处理海洋数据并画图的工具包--ocean_data_tools
matlab 处理海洋数据并画图的工具包–ocean_data_tools matlab 处理海洋数据并画图的工具包–ocean_data_tools ocean_data_tools 简化了提取、格式化和可视化免费可用的海洋学数据的过程。虽然可以在线访问大量海洋学数据,但由于获取这些数据并将其格式化为可用数据…...

多级缓存架构,让系统更快的跑起来!
大家好,今天,咱们来聊聊一个超级实用的话题——多级缓存架构。别一听“架构”俩字就头大,我保证,这篇文章既有趣又易懂,让你秒变缓存小达人! 一、多级缓存,为啥这么火? 在互联网的汪洋大海里,数据就是咱们的宝藏。但每次从数据库里捞数据,都跟挖宝藏似的,慢得很!…...

MCP:AI时代的“万能插座”,开启大模型无限可能
摘要:Model Context Protocol(MCP)由Anthropic在2024年底开源,旨在统一大模型与外部工具、数据源的通信标准。采用客户端-服务器架构,基于JSON-RPC 2.0协议,支持stdio、SSE、Streamable HTTP等多种通信方式…...

使用 PCL 和 Qt 实现点云可视化与交互
下面我将介绍如何结合点云库(PCL)和Qt框架(特别是QML)来实现点云的可视化与交互功能,包括高亮选择等效果。 1. 基本架构设计 首先需要建立一个结合PCL和Qt的基本架构: // PCLQtViewer.h #pragma once#include <QObject> #include <pcl/point…...

静态网页的开发
文章目录 基于 idea 开发静态网页添加web框架前端配置服务器并启动服务资源名字不是 index 静态网页 流转 基于 idea 开发静态网页 添加web框架 方法1 方法2 前端 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8&quo…...

【CPU】结合RISC-V CPU架构回答中断系统的7个问题(个人草稿)
结合RISC-V CPU架构对中断系统七个关键问题的详细解析,按照由浅入深的结构进行说明: 一、中断请求机制(问题①) 硬件基础: RISC-V通过CLINT(Core Local Interrupter)和PLIC(Platfor…...

uCOS3实时操作系统(任务切换和任务API函数)
文章目录 任务切换任务API函数 任务切换 C/OS-III 将 PendSV 的中断优先级配置为最低的中断优先级,这么一来, PendSV 异常的中断服务函数就会在其他所有中断处理完成后才被执行。C/OS-III 就是将任务切换的过程放到 PendSV 异常的中断服务函数中处理的。…...

【Python网络爬虫开发】从基础到实战的完整指南
目录 前言:技术背景与价值当前技术痛点解决方案概述目标读者说明 一、技术原理剖析核心概念图解核心作用讲解关键技术模块技术选型对比 二、实战演示环境配置要求核心代码实现(10个案例)案例1:基础静态页面抓取案例2:动…...

科学养生指南:解锁健康生活新方式
在快节奏的现代生活中,健康养生已成为人们关注的焦点。科学合理的养生方式,能帮助我们增强体质、预防疾病,享受更优质的生活。 饮食是健康养生的基石。遵循 “均衡饮食” 原则,每日饮食需包含谷类、蔬菜水果、优质蛋白质和健康…...

第十四届蓝桥杯 2023 C/C++组 有奖问答
目录 题目: 题目描述: 题目链接: 思路: 核心思路: 思路详解: 代码: 代码详解: 题目: 题目描述: 题目链接: 蓝桥云课 有奖问答 思路&…...

解决Chrome浏览器访问https提示“您的连接不是私密连接”的问题
如何绕过Chrome的“您的连接不是私密连接”证书警告页面 在使用Chrome浏览器访问一些自签名或测试用的HTTPS网站时,常常会遇到这样一个拦截页面: “您的连接不是私密连接” 虽然这是Chrome出于安全考虑的设计,但对于开发者或测试人员来说&am…...

transformer注意力机制
单头注意力机制 import torch import torch.nn.functional as Fdef scaled_dot_product_attention(Q, K, V):# Q: (batch_size, seq_len, d_k)# K: (batch_size, seq_len, d_k)# V: (batch_size, seq_len, d_v)batch_size: 一次输入的句子数。 seq_len: 每个句子的词数。 d_mo…...

QT 5.15 程序打包
说明: windeployqt 是 Qt 提供的一个工具,用于自动收集并复制运行 Qt 应用程序所需的动态链接库(.dll 文件)及其他资源(如插件、QML 模块等)到可执行文件所在的目录。这样你就可以将应用程序和这些依赖项一…...

秒杀抢购系统架构与优化全解:从业务特性到技术落地
一、秒杀抢购业务的本质 秒杀,顾名思义,就是“以秒为单位”的限时限量抢购活动。它的核心是短时间内聚集高流量,以超低价格进行引流。 这种业务场景对系统架构提出了极高的要求,主要表现为: 高并发访问量 极短的处理…...

【路由交换方向IE认证】BGP选路原则之AS-Path属性
文章目录 一、路由器BGP路由的处理过程控制平面和转发平面选路工具 二、BGP的选路顺序选路的前提选路顺序 三、AS-Path属性选路原则AS-Path属性特性AS-Path管进还是管出呢?使用AS-Path对进本AS的路由进行选路验证AS-Path不接收带本AS号的路由 四、BGP邻居建立配置 一…...

Spark-SQL与Hive
Spark-SQL与Hive的那些事儿:从连接到数据处理 在大数据处理领域,Spark-SQL和Hive都是非常重要的工具。今天咱们就来聊聊它们之间的关系,以及怎么用Spark-SQL去连接Hive进行数据处理。先说说Hive,它是Hadoop上的SQL引擎࿰…...

Linux系统下docker 安装 redis
docker安装最新版的redis 一、docker拉取最新版redis镜像 拉取镜像若没有指定版本,代表拉取最新版本 二、查询redis镜像 三、挂载配置文件 在docker容器内修改redis配置文件不方便,所以挂载配置文件,这样可以在外边修改redis配置 3.1 创建…...

【阿里云大模型高级工程师ACP习题集】2.1 用大模型构建新人答疑机器人
练习题 【单选题】1. 在调用通义千问大模型时,将API Key存储在环境变量中的主要目的是? A. 方便在代码中引用 B. 提高API调用的速度 C. 增强API Key的安全性 D. 符合阿里云的规定 【多选题】2. 以下哪些属于大模型在问答场景中的工作阶段?( ) A. 输入文本分词化 B. Toke…...

深度学习框架PyTorch——从入门到精通(3.3)YouTube系列——自动求导基础
这部分是 PyTorch介绍——YouTube系列的内容,每一节都对应一个youtube视频。(可能跟之前的有一定的重复) 我们需要Autograd做什么?一个简单示例训练中的自动求导开启和关闭自动求导自动求导与原地操作 自动求导分析器高级主题&…...

【基础算法】二分算法详解
🎯 前言:二分不是找某个数,而是找一个满足条件的位置/值 所以最关键的是:找到单调性,写好 check() 函数,剩下交给模板! 什么是二分算法 二分算法是一种在有序区间中查找答案的方法,时间复杂度:O(log n)。核心思想是: 每次把搜索区间分成两半,只保留可能存在答案的…...

mysql——基础知识
关键字大小写不敏感 查看表结构中的 desc describe 描述 降序中的 desc descend 1. 数据库的操作 1. 创建数据库 create database 数据库名;为防止创建的数据库重复 CREATE DATABASE IF NOT EXISTS 数据库名;手动设置数据库采用的字符集 character set 字符集名;chars…...

html+js+clickhouse环境搭建
实验背景: 我目前有一台服务器A,和一台主机B,两台设备属于同一局域网,相互之间可以通讯。服务器A中部署着clickhouse,我在主机B中想直接通过javascript代码访问服务器中的clickhouse数据库并获取数据。 ClickHouse 服务…...

JWT算法详解
JWT(JSON Web Token)的整个算法流程主要基于其签名算法。以最常见的签名算法HS256(HMAC SHA256)为例,以下是详细的算法流程,涵盖编码、签名和验证过程: 编码 构造头部(Header&#x…...

OOA-CNN-LSTM-Attention、CNN-LSTM-Attention、OOA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比
OOA-CNN-LSTM-Attention、CNN-LSTM-Attention、OOA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比 目录 OOA-CNN-LSTM-Attention、CNN-LSTM-Attention、OOA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比预测效果基本介绍程序设计参考资料 预测效果 基本介绍 基于OOA-CN…...

Python Cookbook-6.6 在代理中托管特殊方法
任务 在新风格对象模型中,Python 操作其实是在类中查找特殊方法的(而不是在实例中那是经典对象模型的处理方式)。现在,需要将一些新风格的实例包装到代理类中,此代理可以选择将一些特殊方法委托给内部的被包装对象。 解决方案 你需要即时地…...

PCIE Spec ---Base Address Registers
7.5.1.2.1 Base Address Registers (Offset 10h - 24h) 在 boot 到操作系统之前,系统软件需要生产一个内存映射的 address map ,用于告诉系统有多少内存资源,以及相应功能需要的内存空间,所以在设备的 PCI 内存空间中就有了这个 …...
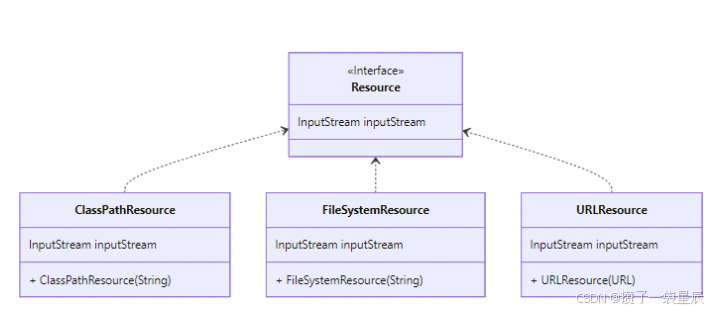
Spring如何通过XML注册Bean
在上一篇当中我们完成了对三种资源文件的读写 上篇内容:Spring是如何实现资源文件的加载 Test public void testClassPathResource() throws IOException { DefaultResourceLoader defaultResourceLoader new DefaultResourceLoader(); Resource resource …...

理解 `#pragma pack`:C/C++内存对齐的钥匙
引言:为什么我的网络程序收发的数据总是错位? 在网络编程中,你是否遇到过这样的困惑:明明发送方和接收方的结构体定义完全一样,但解析出来的数据却乱七八糟?这很可能是因为内存对齐在作祟。今天我们就来深…...
