每日一题:两个仓库的最低配送费用问题
文章目录
- 两个仓库的最低配送费用问题
- 一、问题描述
- 二、解题思路
- (一)初始假设
- (二)差值定义
- (三)选择最优
- (四)计算答案
- 三、代码实现
- 四、代码分析
- (一)输入处理
- (二)初始费用计算
- (三)差值计算与排序
- (四)选择最小差值并计算额外费用
- (五)输出结果
- 五、总结
两个仓库的最低配送费用问题
一、问题描述
某公司有 2 个仓库(用 A 和 B 表示),需要给 m 个营业网点(m 为偶数)各配送一件货物。每个仓库正好有 m/2 件货物。配送给不同营业网点的费用使用一个二维数组 cost 表示,其中 cost[i] = [Ai, Bi] 表示第 i 个营业网点从 A 仓发货的运费为 Ai,从 B 仓库发货的费用为 Bi。任务是计算 m 件货物配送的最低费用,要求每个营业网点都有一件货物送到。
二、解题思路
(一)初始假设
若全部从仓库 A 发货,则总费用为 (\sum_{i=1}^{m} A_i)。
(二)差值定义
将第 i 个网点改为从 B 发货,相当于在全部发自 A 的基准上“多花” (\Delta_i = B_i - A_i) 的费用。
(三)选择最优
需要有且仅有 m/2 件货物由 B 发货。为了使额外总费用最小,应当选取最小的 m/2 个 (\Delta_i)(即最负或最小的那些差值)去改由 B 发货。
(四)计算答案
- 计算全部从 A 发货的初始费用。
- 计算每个网点从 B 发货相对于从 A 发货的差值。
- 对差值进行排序,选择最小的 m/2 个差值对应的网点从 B 发货。
- 将这些最小差值累加到初始费用上,得到最终的最低总费用。
三、代码实现
#include <bits/stdc++.h> // 包含了 C++ 标准库中的大部分头文件,方便使用各种功能
using namespace std; // 使用标准命名空间,避免每次调用标准库函数或对象时都要加 std::int main() {int m; // 定义变量 m,表示营业网点的数量cin >> m; // 从标准输入读取 m 的值string line; // 定义一个字符串变量 line,用于存储输入的数组字符串// 读取第二行的数组字符串getline(cin, line); // 读取并丢弃之前读取 m 后的换行符getline(cin, line); // 真正读取包含成本数据的行vector<pair<int, int>> cost; // 定义一个向量,用于存储每个营业网点从 A 和 B 仓库发货的费用vector<int> nums; // 定义一个向量,用于存储从输入字符串中提取的所有整数int num = 0; // 定义一个变量 num,用于临时存储当前正在解析的数字bool inNum = false; // 定义一个布尔变量 inNum,用于标记是否正在解析一个数字// 遍历输入的字符串,提取所有整数for (char c : line) { // 遍历字符串中的每个字符if (isdigit(c)) { // 如果当前字符是数字num = num * 10 + (c - '0'); // 将当前字符转换为数字并累加到 num 中inNum = true; // 标记正在解析一个数字} else if (inNum) { // 如果当前字符不是数字,但之前正在解析一个数字nums.push_back(num); // 将解析完成的数字存储到 nums 向量中num = 0; // 重置 num 为 0,准备解析下一个数字inNum = false; // 重置 inNum 为 false,表示当前不再解析数字}}if (inNum) nums.push_back(num); // 如果字符串末尾是一个数字,将其存储到 nums 向量中// 两两配对成 cost[i]for (int i = 0; i < nums.size(); i += 2) { // 遍历 nums 向量,每次跳过两个元素cost.emplace_back(nums[i], nums[i + 1]); // 将每两个连续的数字作为一对,存储到 cost 向量中}// 1. 计算全部从 A 发货的初始费用long long sumA = 0; // 定义一个变量 sumA,用于存储全部从 A 发货的总费用for (auto &p : cost) { // 遍历 cost 向量sumA += p.first; // 将每个营业网点从 A 仓库发货的费用累加到 sumA 中}// 2. 计算差值数组 Δ[i] = B_i - A_ivector<int> diff; // 定义一个向量,用于存储每个营业网点从 B 发货相对于从 A 发货的差值for (auto &p : cost) { // 遍历 cost 向量diff.push_back(p.second - p.first); // 计算差值并存储到 diff 向量中}// 3. 对差值排序,取最小的 m/2 个sort(diff.begin(), diff.end()); // 对 diff 向量进行升序排序long long extra = 0; // 定义一个变量 extra,用于存储额外的费用for (int i = 0; i < m / 2; ++i) { // 遍历 diff 向量的前 m/2 个元素extra += diff[i]; // 将最小的 m/2 个差值累加到 extra 中}// 4. 输出最小总费用cout << (sumA + extra) << endl; // 将初始费用 sumA 和额外费用 extra 相加,输出最终的最低总费用return 0; // 程序正常结束,返回 0
}
四、代码分析
(一)输入处理
- 使用
getline读取包含成本数据的行,并通过逐字符判断来提取其中的数字,将其存入nums向量。 - 然后将
nums中的数字两两配对,形成cost向量,其中每个元素是一个包含两个整数的pair,分别表示从 A 仓库和 B 仓库发货到对应营业网点的费用。
(二)初始费用计算
- 遍历
cost向量,将每个网点从 A 仓库发货的费用累加,得到全部从 A 发货的初始总费用sumA。
(三)差值计算与排序
- 遍历
cost向量,计算每个网点从 B 仓库发货相对于从 A 仓库发货的差值,并将这些差值存入diff向量。 - 对
diff向量进行排序,以便后续选择最小的 m/2 个差值。
(四)选择最小差值并计算额外费用
- 遍历排序后的
diff向量的前 m/2 个元素,将这些最小差值累加到extra中,extra表示从 A 仓库发货改为从 B 仓库发货带来的额外费用。
(五)输出结果
- 将初始费用
sumA与额外费用extra相加,得到最终的最低总费用,并输出。
五、总结
本题通过巧妙地利用差值和排序,将问题转化为选择最小的 m/2 个差值来最小化额外费用,从而高效地求解出最低配送费用。这种方法不仅思路清晰,而且时间复杂度较低,适合处理大规模数据。
相关文章:

每日一题:两个仓库的最低配送费用问题
文章目录 两个仓库的最低配送费用问题一、问题描述二、解题思路(一)初始假设(二)差值定义(三)选择最优(四)计算答案 三、代码实现四、代码分析(一)输入处理&a…...

华为私有协议Hybrid
实验top图 理论环节 1. 基本概念 Hybrid接口: 支持同时处理多个VLAN流量,且能针对不同VLAN配置是否携带标签(Tagged/Untagged)。 核心特性: 灵活控制数据帧的标签处理方式,适用于复杂网络场景。 2. 工作…...

Redis 基本数据类型解析
Redis 是一个高效的内存数据存储系统,广泛应用于缓存、消息队列、排行榜、实时数据处理等场景。其高性能的特点部分源自其丰富的数据结构,Redis 提供了多种数据类型,能够支持不同的使用需求。本文将详细介绍 Redis 的八种基本数据类型。 1. …...

数据库实验10
设计性实验 1.实验要求 1.编写函数FsumXXX,1~n(参数)求和; GO CREATE FUNCTION Fsum065 (n INT) RETURNS INT AS BEGIN DECLARE sum INT 0 WHILE n > 0 BEGIN SET sum sum n SET n n - 1 END RETURN sum END …...

Yocto是如何使用$D目录来构建文件系统的?
Yocto最终会将所有Recipe的${D}(部署目录)下的文件整合到根文件系统中,但这一过程并非简单收集所有内容,而是通过分阶段打包、依赖管理和定制化配置实现的。以下是核心机制的解析: 一、${D}目录的作用与文件收集原理 ${D}的定位 ${D}是模拟目标系统根文件结构的临时目录(…...

jflash下载时出现 Could not read unit serial number! 的解决方法
出现的原因是由于Jlink原厂固件SN码是-1 我用的版本是v6.40 解决方法:添加序列号 1.打开:J-Link commander 之后在命令栏输入:exec setsnxxxxxxxx 2.添加序列号到license,打开J-Link License Manager V6.40 jlink-v640下载软件…...

Linux 信号终篇(总结)
前文:本文是对信号从产生到被处理的过程中的概念和原理的总结,如果想了解具体实现,请查看前两篇博客:Linux 信号-CSDN博客、Linux 信号(下篇)-CSDN博客 一、信号的产生 1.1 信号产生的五种条件 ①键盘组…...

使用Kotlin Flow实现Android应用的响应式编程
在Android应用中使用Kotlin Flow实现响应式编程可以分为以下步骤,结合最佳实践和生命周期管理: 1. 添加依赖 在build.gradle中确保包含协程和生命周期相关依赖: dependencies {implementation("org.jetbrains.kotlinx:kotlinx-corouti…...

react中的用法——setDisabled dva dispatch effects
setDisabled 在react中,setDisabled通常是指通过状态管理来控制某个组件(如按钮、输入框等)的禁用状态。虽然react本身没有内置的setDisabled方法,但你可以使用useState钩子来实现类似的功能。以下是一个简单的示例,展…...
Java Object类的使用全面解析)
(九)Java Object类的使用全面解析
一、Object类概述 1.1 Object类在Java中的地位 在Java语言中,Object类是所有类的超类,位于类继承树的顶端。它是Java类层次结构中的根类,每个类都直接或间接继承自Object类。当我们定义一个类时,如果没有明确使用extends关键字指…...

LVGL对象(Objects)
文章目录 🧱 一、LVGL 中的对象(lv\_obj)🔹 lv\_obj\_t 的作用 🧩 二、对象的分类结构(类比继承)🧰 三、对象的创建与销毁✅ 创建对象示例:创建一个按钮❌ 删除对象 &…...

自然语言到 SQL 转换:开启智能数据库交互新时代
引言 随着人工智能技术的飞速发展,自然语言处理(NLP)领域取得了显著的进步。其中,将自然语言转换为 SQL 语句的技术尤为引人注目。这种技术能够帮助用户,尤其是那些不熟悉 SQL 的业务人员,快速从数据库中获…...

服务器配置错误导致SSL/TLS出现安全漏洞,如何进行排查?
SSL/TLS 安全漏洞排查与修复指南 一、常见配置错误类型 弱加密算法与密钥问题 使用弱密码套件(如DES、RC4)或密钥长度不足(如RSA密钥长度<2048位),导致加密强度不足。 密钥管理不当(如私钥未加密存…...

路由重发布
路由重发布 实验目标: 掌握路由重发布的配置方法和技巧; 掌握通过路由重发布方式实现网络的连通性; 熟悉route-pt路由器的使用方法; 实验背景:假设学校的某个分区需要配置简单的rip协议路由信息,而主校…...
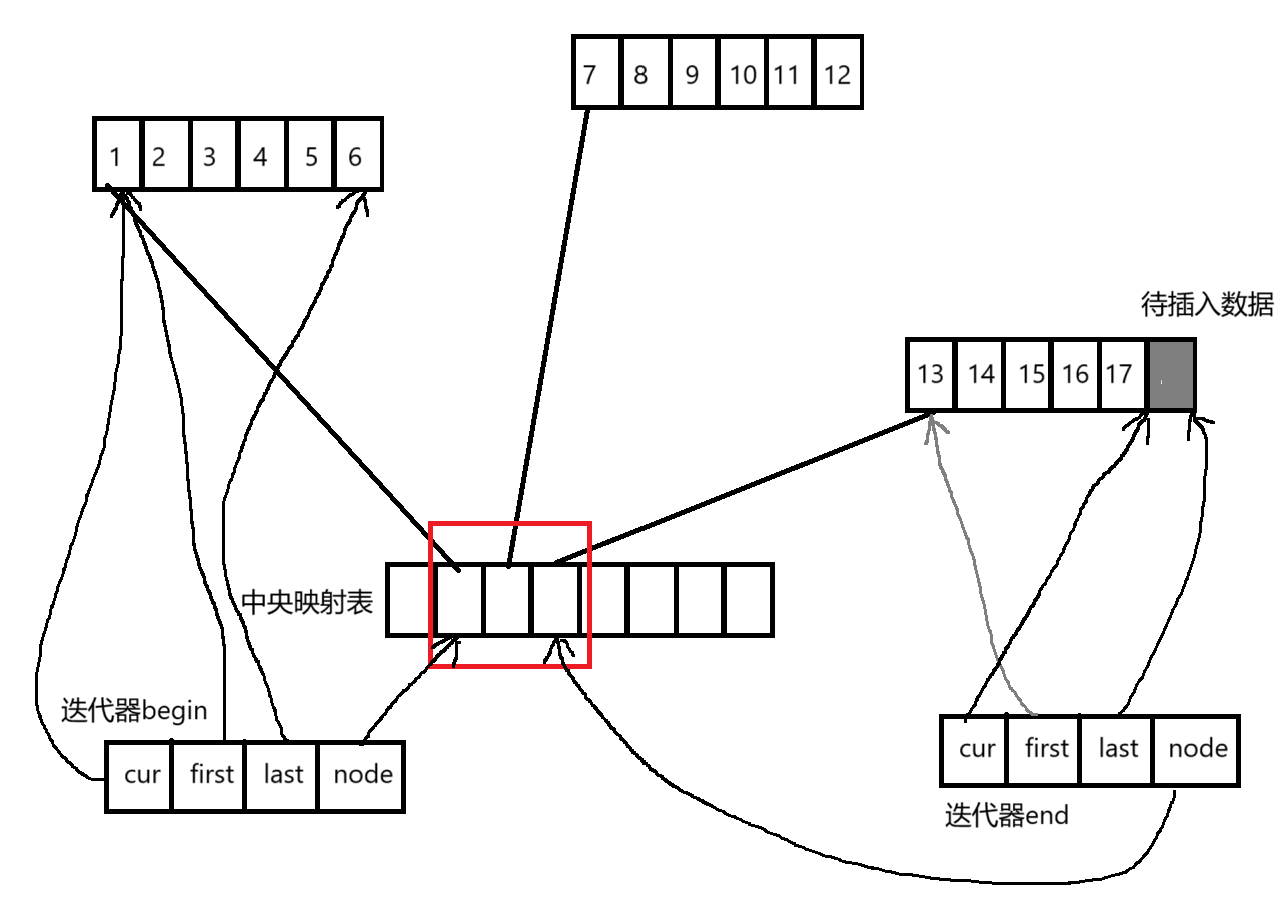
C++修炼:stack和queue
Hello大家好!很高兴我们又见面啦!给生活添点passion,开始今天的编程之路! 我的博客:<但凡. 我的专栏:《编程之路》、《数据结构与算法之美》、《题海拾贝》、《C修炼之路》 欢迎点赞,关注&am…...

【软件工程】基于频谱的缺陷定位
基于频谱的缺陷定位(Spectrum-Based Fault Localization, SBFL)是一种通过分析程序执行覆盖信息(频谱数据)来定位代码中缺陷的方法。其核心思想是:通过测试用例的执行结果(成功/失败)和代码覆盖…...

【计算机视觉】优化MVSNet可微分代价体以提高深度估计精度的关键技术
优化MVSNet可微分代价体以提高深度估计精度的关键技术 1. 代价体基础理论与分析1.1 标准代价体构建1.2 关键问题诊断 2. 特征表示优化2.1 多尺度特征融合2.2 注意力增强匹配 3. 代价体构建优化3.1 自适应深度假设采样3.2 可微分聚合操作改进 4. 正则化与优化策略4.1 多尺度代价…...

为什么tcp不能两次握手
TCP **不能用“两次握手”**的根本原因是:两次握手无法确保双方“都知道”连接是可靠建立的,容易引发“旧连接请求”造成错误连接。 🔁 先看标准的 三次握手(3-Way Handshake)流程 客户端 服务器| …...

常见音频主控芯片以及相关厂家总结
音频主控芯片是音频设备(如蓝牙耳机、音箱、功放等)的核心组件,负责音频信号的解码、编码、处理和传输。以下是常见的音频主控芯片及其相关厂家,按应用领域分类: 蓝牙音频芯片 主要用于无线耳机、音箱等设备࿰…...

掌握 Kubernetes 和 AKS:热门面试问题和专家解答
1. 在 AKS(Azure Kubernetes 服务)中,集群、节点、Pod 和容器之间的关系和顺序是什么? 在 AKS(Azure Kubernetes 服务)中,集群、节点、Pod 和容器之间的关系和顺序如下: 集群&#…...

【MyBatis-7】深入理解MyBatis二级缓存:提升应用性能的利器
在现代应用开发中,数据库访问往往是性能瓶颈之一。作为Java生态中广泛使用的ORM框架,MyBatis提供了一级缓存和二级缓存机制来优化数据库访问性能。本文将深入探讨MyBatis二级缓存的工作原理、配置方式、使用场景以及最佳实践,帮助开发者充分利…...

5.9-selcct_poll_epoll 和 reactor 的模拟实现
5.9-select_poll_epoll 本文演示 select 等 io 多路复用函数的应用方法,函数具体介绍可以参考我过去写的博客。 先绑定监听的文件描述符 int sockfd socket(AF_INET, SOCK_STREAM, 0); struct sockaddr_in serveraddr; memset(&serveraddr, 0, sizeof(struc…...
》阅读笔记:p17-p27)
《算法导论(第4版)》阅读笔记:p17-p27
《算法导论(第4版)》学习第 10 天,p17-p27 总结,总计 11 页。 一、技术总结 1. insertion sort (1)keys The numbers to be sorted are also known as the keys(要排序的数称为key)。 第 n 次看插入排序,这次有两个地方感触比较深&#…...

软考错题集
一个有向图具有拓扑排序序列,则该图的邻接矩阵必定为()矩阵。 A.三角 B.一般 C.对称 D.稀疏矩阵的下三角或上三角部分包含非零元素,而其余部分为零。一般矩阵这个术语太过宽泛,不具体指向任何特定性 质的矩阵。对称矩阵…...

T2I-R1:通过语义级与图像 token 级协同链式思维强化图像生成
文章目录 速览摘要1 引言2 相关工作统一生成与理解的 LMM(Unified Generation and Understanding LMM.)用于大型推理模型的强化学习(Reinforcement Learning for Large Reasoning Models.)3 方法3.1 预备知识3.2 语义级与令牌级 CoT语义级 CoT(Semantic-level CoT)令牌级…...

Dockers部署oscarfonts/geoserver镜像的Geoserver
Dockers部署oscarfonts/geoserver镜像的Geoserver 说实话,最后发现要选择合适的Geoserver镜像才是关键,所以所以所以…🐷 推荐oscarfonts/geoserver的镜像! 一开始用kartoza/geoserver镜像一直提示内存不足,不过还好…...

【脑机接口临床】脑机接口手术的风险?脑机接口手术的应用场景?脑机接口手术如何实现偏瘫康复?
脑机接口的应用 通常对脑机接口感兴趣的两类人群,一类是适应症患者 ,另一类是科技爱好者。 1 意念控制外部设备 常见的外部设备有:外骨骼、机械手、辅助康复设备、电刺激设备、电脑光标、轮椅。 2 辅助偏瘫康复或辅助脊髓损伤患者意念控制…...

扩增子分析|微生物生态网络稳定性评估之鲁棒性(Robustness)和易损性(Vulnerability)在R中实现
一、引言 周集中老师团队于2021年在Nature climate change发表的文章,阐述了网络稳定性评估的原理算法,并提供了完整的代码。自此对微生物生态网络的评估具有更全面的指标,自此网络稳定性的评估广受大家欢迎。本系列将介绍网络稳定性之鲁棒性…...

Client 和 Server 的关系理解
client.py 和 server.py 是基于 MCP(Multi-Component Protocol)协议的客户端-服务端架构,二者的关系如下: 1. 角色分工 server.py:服务端,负责注册和实现各种“工具函数”(如新闻检索、情感分…...

【含文档+PPT+源码】基于微信小程序的社区便民防诈宣传系统设计与实现
项目介绍 本课程演示的是一款基于微信小程序的社区便民防诈宣传系统设计与实现,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的 Java 学习者。 1.包含:项目源码、项目文档、数据库脚本、软件工具等所有资料 2.带你从零开始部署运行本套…...
