当前位置：首页 > article >正文

yocto的每个recipe都是在工作路径中完成

article 2025/10/5 1:53:07

Yocto项目中每个Recipe的编译过程都会将源文件解压或搬运到tmp/work/下的特定工作目录，并在此完成所有构建任务。具体流程可分为以下关键步骤：

一、源码处理阶段

源码获取（do_fetch）
Recipe通过SRC_URI变量指定源码来源（如Git仓库、HTTP下载或本地文件）。这些文件会被下载到DL_DIR（默认路径为build/downloads/），并生成.done文件标记完成状态²7。
示例：若源码来自Git仓库，BitBake会克隆代码到DL_DIR/git2/目录下。
源码解压（do_unpack）
源码会被解压到tmp/work/<target-arch>/<recipe-name>/<version>-r<revision>/目录下的WORKDIR中²6。例如，helloworld_1.0.bb的源码会解压到work/x86_64-linux/helloworld/1.0-r0/路径。此目录包含：
- ${S}：源码主目录（如

yocto的每个recipe都是在工作路径中完成

Yocto项目中每个Recipe的编译过程都会将源文件解压或搬运到tmp/work/下的特定工作目录，并在此完成所有构建任务。具体流程可分为以下关键步骤：一、源码处理阶段源码获取（do_fetch） Recipe通过SRC_URI变量指定源码来源（如Git仓库、HTTP下载或本地文件）。这些文件会被下载…...

编程日记 2025/8/1 1:37:26

玩转Docker | 使用Docker部署DailyTxT日记工具

玩转Docker | 使用Docker部署DailyTxT日记工具一、DailyTxT介绍DailyTxT简介DailyTxT 特点二、系统要求环境要求环境检查Docker版本检查检查操作系统版本三、部署DailyTxT服务下载DailyTxT镜像编辑部署文件创建容器检查容器状态检查服务端口安全设置四、访问DailyTxT服务访问D…...

编程日记 2025/8/20 21:15:06

初等数论--欧拉定理及证明

0. 证明前置知识同余类（剩余类） r n ‾ { x ∣ x m n r , m ∈ Z } \overline{r_n} \{ x| xmnr,m \in Z\} rn{x∣xmnr,m∈Z} r n ‾ \overline{r_n} rn表示模 n n n后余 r r r的同余类（剩余类） 比如 2 5 ‾ { ⋯…...

编程日记 2025/7/3 21:59:26

Oracle非归档模式遇到文件损坏怎么办？

昨天夜里基地夜班的兄弟，打电话说有个报表库连不上了，赶紧起来连上VPN查看一下，看到实例宕机了，先赶紧startup起来。 1.查看报错信息环境介绍：Redhat 6.9 Oracle 11.2.0.4 No Archive Mode 查看alert log 关键报…...

编程日记 2025/9/24 13:01:26

机器人领域和心理学领域恐怖谷是什么

机器人领域和心理学领域恐怖谷是什么恐怖谷是一个在机器人领域和心理学领域备受关注的概念，由日本机器人专家森政弘于1970年提出。含义当机器人与人类的相似度达到一定程度时，人类对它们的情感反应会突然从积极变为消极，产生一种毛骨悚然、厌恶恐惧的感觉。这种情感…...

编程日记 2025/7/3 12:08:27

树莓派4的v4l2摄像头（csi）no cameras available，完美解决

根据2025年最新技术文档和树莓派官方支持建议，no cameras available错误通常由驱动配置冲突或硬件连接问题导致。以下是系统化解决方案： 一、核心修复步骤强制禁用传统驱动 sudo nano /boot/firmware/config.txt确保包含以下配置（2025年新版…...

编程日记 2025/9/13 23:23:11

每日一题：两个仓库的最低配送费用问题

文章目录两个仓库的最低配送费用问题一、问题描述二、解题思路（一）初始假设（二）差值定义（三）选择最优（四）计算答案三、代码实现四、代码分析（一）输入处理&a…...

编程日记 2025/6/5 3:35:13

华为私有协议Hybrid

实验top图理论环节 1. 基本概念 Hybrid接口： 支持同时处理多个VLAN流量，且能针对不同VLAN配置是否携带标签（Tagged/Untagged）。核心特性： 灵活控制数据帧的标签处理方式，适用于复杂网络场景。 2. 工作…...

编程日记 2025/10/4 9:16:25

Redis 基本数据类型解析

Redis 是一个高效的内存数据存储系统，广泛应用于缓存、消息队列、排行榜、实时数据处理等场景。其高性能的特点部分源自其丰富的数据结构，Redis 提供了多种数据类型，能够支持不同的使用需求。本文将详细介绍 Redis 的八种基本数据类型。 1. …...

编程日记 2025/10/2 7:55:54

数据库实验10

设计性实验 1．实验要求 1.编写函数FsumXXX，1~n（参数）求和； GO CREATE FUNCTION Fsum065 (n INT) RETURNS INT AS BEGIN DECLARE sum INT 0 WHILE n > 0 BEGIN SET sum sum n SET n n - 1 END RETURN sum END …...

编程日记 2025/9/30 12:32:24

Yocto是如何使用＄D目录来构建文件系统的？

Yocto最终会将所有Recipe的${D}（部署目录）下的文件整合到根文件系统中，但这一过程并非简单收集所有内容，而是通过分阶段打包、依赖管理和定制化配置实现的。以下是核心机制的解析：一、${D}目录的作用与文件收集原理 ${D}的定位 ${D}是模拟目标系统根文件结构的临时目录（…...

编程日记 2025/8/12 22:22:36

jflash下载时出现 Could not read unit serial number! 的解决方法

出现的原因是由于Jlink原厂固件SN码是-1 我用的版本是v6.40 解决方法：添加序列号 1.打开：J-Link commander 之后在命令栏输入：exec setsnxxxxxxxx 2.添加序列号到license，打开J-Link License Manager V6.40 jlink-v640下载软件…...

编程日记 2025/10/1 1:38:51

Linux 信号终篇（总结）

前文：本文是对信号从产生到被处理的过程中的概念和原理的总结，如果想了解具体实现，请查看前两篇博客：Linux 信号-CSDN博客、Linux 信号（下篇）-CSDN博客一、信号的产生 1.1 信号产生的五种条件 ①键盘组…...

编程日记 2025/9/30 22:26:37

使用Kotlin Flow实现Android应用的响应式编程

在Android应用中使用Kotlin Flow实现响应式编程可以分为以下步骤，结合最佳实践和生命周期管理： 1. 添加依赖在build.gradle中确保包含协程和生命周期相关依赖： dependencies {implementation("org.jetbrains.kotlinx:kotlinx-corouti…...

编程日记 2025/7/2 10:00:46

react中的用法——setDisabled dva dispatch effects

setDisabled 在react中，setDisabled通常是指通过状态管理来控制某个组件（如按钮、输入框等）的禁用状态。虽然react本身没有内置的setDisabled方法，但你可以使用useState钩子来实现类似的功能。以下是一个简单的示例，展…...

编程日记 2025/7/20 1:29:59

（九）Java Object类的使用全面解析

一、Object类概述 1.1 Object类在Java中的地位在Java语言中，Object类是所有类的超类，位于类继承树的顶端。它是Java类层次结构中的根类，每个类都直接或间接继承自Object类。当我们定义一个类时，如果没有明确使用extends关键字指…...

编程日记 2025/10/4 19:41:58

LVGL对象（Objects）

文章目录 🧱 一、LVGL 中的对象（lv\_obj）🔹 lv\_obj\_t 的作用 🧩 二、对象的分类结构（类比继承）🧰 三、对象的创建与销毁✅ 创建对象示例：创建一个按钮❌ 删除对象 &…...

编程日记 2025/9/30 10:54:07

自然语言到 SQL 转换：开启智能数据库交互新时代

引言随着人工智能技术的飞速发展，自然语言处理（NLP）领域取得了显著的进步。其中，将自然语言转换为 SQL 语句的技术尤为引人注目。这种技术能够帮助用户，尤其是那些不熟悉 SQL 的业务人员，快速从数据库中获…...

编程日记 2025/9/8 4:53:14

服务器配置错误导致SSL/TLS出现安全漏洞，如何进行排查？

SSL/TLS 安全漏洞排查与修复指南一、常见配置错误类型‌ 弱加密算法与密钥问题‌ 使用弱密码套件（如DES、RC4）或密钥长度不足（如RSA密钥长度<2048位），导致加密强度不足。密钥管理不当（如私钥未加密存…...

编程日记 2025/9/30 12:32:44

路由重发布

路由重发布实验目标： 掌握路由重发布的配置方法和技巧； 掌握通过路由重发布方式实现网络的连通性； 熟悉route-pt路由器的使用方法； 实验背景：假设学校的某个分区需要配置简单的rip协议路由信息，而主校…...

编程日记 2025/10/1 2:57:25

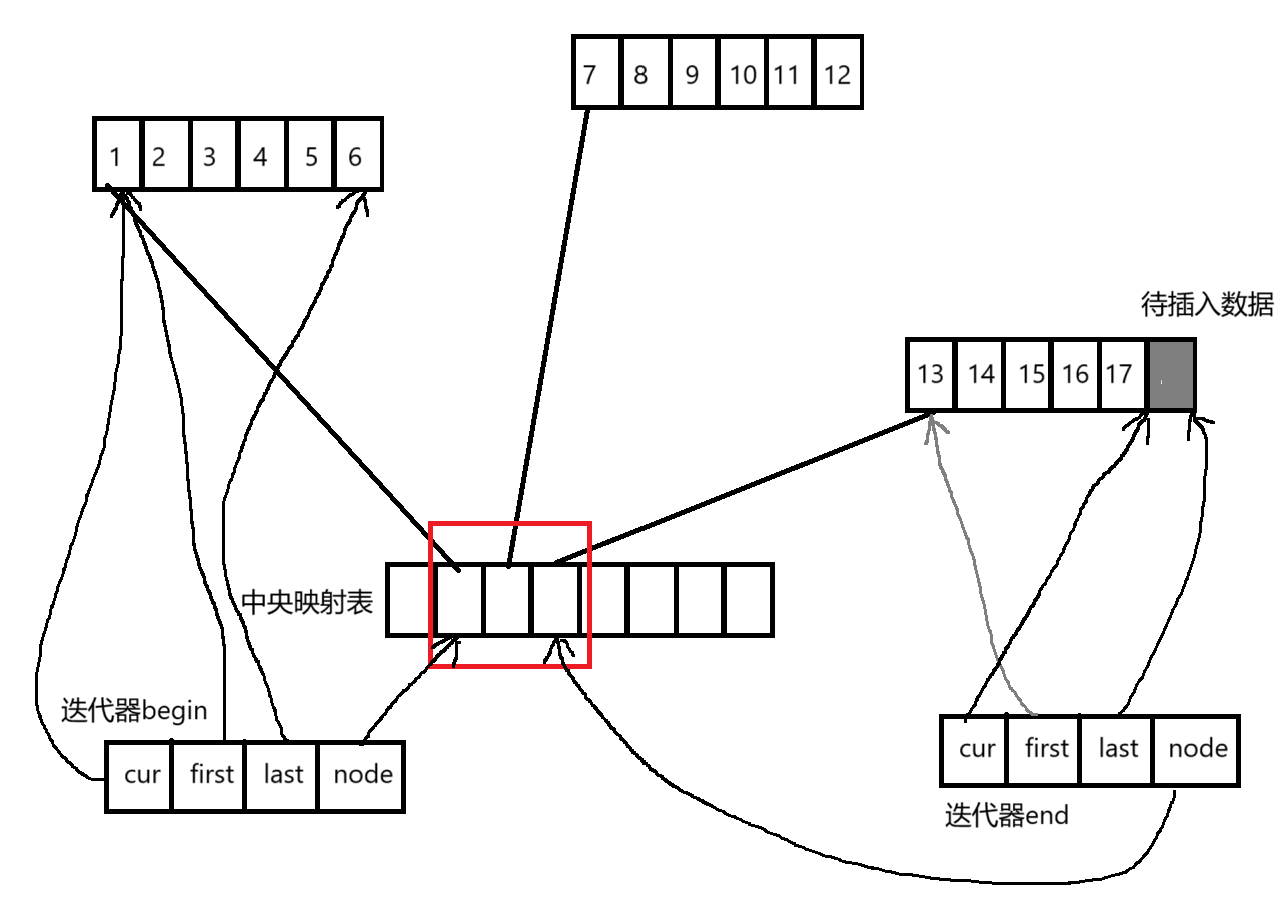
C++修炼：stack和queue

Hello大家好！很高兴我们又见面啦！给生活添点passion，开始今天的编程之路！ 我的博客：<但凡. 我的专栏：《编程之路》、《数据结构与算法之美》、《题海拾贝》、《C修炼之路》欢迎点赞，关注&am…...

编程日记 2025/9/30 12:31:48

【软件工程】基于频谱的缺陷定位

基于频谱的缺陷定位（Spectrum-Based Fault Localization, SBFL）是一种通过分析程序执行覆盖信息（频谱数据）来定位代码中缺陷的方法。其核心思想是：通过测试用例的执行结果（成功/失败）和代码覆盖…...

编程日记 2025/8/21 19:28:06

【计算机视觉】优化MVSNet可微分代价体以提高深度估计精度的关键技术

优化MVSNet可微分代价体以提高深度估计精度的关键技术 1. 代价体基础理论与分析1.1 标准代价体构建1.2 关键问题诊断 2. 特征表示优化2.1 多尺度特征融合2.2 注意力增强匹配 3. 代价体构建优化3.1 自适应深度假设采样3.2 可微分聚合操作改进 4. 正则化与优化策略4.1 多尺度代价…...

编程日记 2025/9/30 16:02:05

为什么tcp不能两次握手

TCP **不能用“两次握手”**的根本原因是：两次握手无法确保双方“都知道”连接是可靠建立的，容易引发“旧连接请求”造成错误连接。 🔁 先看标准的三次握手（3-Way Handshake）流程客户端服务器| …...

编程日记 2025/7/16 23:07:54

常见音频主控芯片以及相关厂家总结

音频主控芯片是音频设备（如蓝牙耳机、音箱、功放等）的核心组件，负责音频信号的解码、编码、处理和传输。以下是常见的音频主控芯片及其相关厂家，按应用领域分类： 蓝牙音频芯片主要用于无线耳机、音箱等设备&#xff0…...

编程日记 2025/7/19 9:51:21

掌握 Kubernetes 和 AKS：热门面试问题和专家解答

1. 在 AKS（Azure Kubernetes 服务）中，集群、节点、Pod 和容器之间的关系和顺序是什么？ 在 AKS（Azure Kubernetes 服务）中，集群、节点、Pod 和容器之间的关系和顺序如下： 集群&#…...

编程日记 2025/6/5 9:04:31

【MyBatis-7】深入理解MyBatis二级缓存：提升应用性能的利器

在现代应用开发中，数据库访问往往是性能瓶颈之一。作为Java生态中广泛使用的ORM框架，MyBatis提供了一级缓存和二级缓存机制来优化数据库访问性能。本文将深入探讨MyBatis二级缓存的工作原理、配置方式、使用场景以及最佳实践，帮助开发者充分利…...

编程日记 2025/9/14 9:08:59

5.9-selcct_poll_epoll 和 reactor 的模拟实现

5.9-select_poll_epoll 本文演示 select 等 io 多路复用函数的应用方法，函数具体介绍可以参考我过去写的博客。先绑定监听的文件描述符 int sockfd socket(AF_INET, SOCK_STREAM, 0); struct sockaddr_in serveraddr; memset(&serveraddr, 0, sizeof(struc…...

编程日记 2025/8/16 14:36:34

《算法导论(第4版)》阅读笔记：p17-p27

《算法导论(第4版)》学习第 10 天，p17-p27 总结，总计 11 页。一、技术总结 1. insertion sort (1)keys The numbers to be sorted are also known as the keys(要排序的数称为key)。第 n 次看插入排序，这次有两个地方感触比较深&#…...

编程日记 2025/7/24 4:41:31

软考错题集

一个有向图具有拓扑排序序列，则该图的邻接矩阵必定为（）矩阵。 A.三角 B.一般 C.对称 D.稀疏矩阵的下三角或上三角部分包含非零元素，而其余部分为零。一般矩阵这个术语太过宽泛，不具体指向任何特定性质的矩阵。对称矩阵…...

编程日记 2025/10/4 2:50:31

相关文章：