每日算法刷题 Day3 5.11:leetcode数组2道题,用时1h(有点慢)
5.LC 零矩阵(中等)
面试题 01.08. 零矩阵 - 力扣(LeetCode)
思想:
法一:
利用两个集合分别储存要清0的行和列索引
另外两种原地优化空间的做法暂时不是目前刷题目标,故不考虑
代码
c++:
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {set<int> hang;set<int> lie;int n = matrix.size(), m = matrix[0].size();for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (matrix[i][j] == 0) {hang.insert(i);lie.insert(j);}}}for (const auto& x : hang) {for (int j = 0; j < m; ++j) {matrix[x][j] = 0;}}for (const auto& x : lie) {for (int i = 0; i < n; ++i) {matrix[i][x] = 0;}}}
};
python:
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""hang = set()lie = set()n, m = len(matrix), len(matrix[0])for i in range(n):for j in range(m):if matrix[i][j] == 0:hang.add(i)lie.add(j)for x in hang:for j in range(m):matrix[x][j] = 0for x in lie:for i in range(n):matrix[i][x] = 0
相似题
73. 矩阵置零 - 力扣(LeetCode)
6.LC 对角线遍历(中等,学习)
498. 对角线遍历 - 力扣(LeetCode)
思想:
1.n行m列矩阵,因为是按照对角线遍历,但是分析可得有两种对角线遍历方式,从左下到右上和从右上到左下,是由第i条对角线的奇偶决定的,所以按照对角线遍历, i ∈ [ 0 , n + m − 1 ) i \in [0,n+m-1) i∈[0,n+m−1)
2.对于偶数对角线,是从左下到右上的遍历顺序,但又会出现遍历初始位置不同的情况,故再分类
- i<n,说明在左边界,初始位置(i,0)
- i>=n,说明在下边界,初始位置(n-1,i-(n-1))即(n-1,i-n+1)
3.奇数对角线,是从右上到左下的遍历顺序,对偶式即可 - i<m,说明在上边界,初始位置(0,i)
- i>=m,说明在右边界,初始位置(i-m+1,m-1)
代码
c++:
class Solution {
public:vector<int> findDiagonalOrder(vector<vector<int>>& mat) {vector<int> res;int n = mat.size(), m = mat[0].size();for (int i = 0; i < n + m - 1; ++i) {// 右上到左下if (i % 2) {int x = i < m ? 0 : i - m + 1;int y = i < m ? i : m - 1;while (x < n && y >= 0) {res.emplace_back(mat[x][y]);x++;y--;}}// 左下到右上else {int x = i < n ? i : n - 1;int y = i < n ? 0 : i - n + 1;while (y < m && x >= 0) {res.emplace_back(mat[x][y]);x--;y++;}}}return res;}
};
python:
class Solution:def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:n, m = len(mat), len(mat[0])res = []for i in range(n + m - 1):if i % 2 == 1:x = 0 if i < m else i - m + 1y = i if i < m else m - 1while x < n and y >= 0:res.append(mat[x][y])x += 1y -= 1else:y = 0 if i < n else i - n + 1x = i if i < n else n - 1while y < m and x >= 0:res.append(mat[x][y])y += 1x -= 1return resclass Solution:def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:n,m=len(mat),len(mat[0])res=[]for i in range(n+m-1):if i%2==1:x=0 if i<m else i-m+1y=i if i<m else m-1while x<n and y>=0:res.append(mat[x][y])x+=1y-=1else:y=0 if i<n else i-n+1x=i if i<n else n-1while y<m and x>=0:res.append(mat[x][y])y+=1x-=1return res
1.没有三目运算符,要写成x=0 if i<m else i-m+1
2.没有++运算符,要写成x+=1
相关文章:
)
每日算法刷题 Day3 5.11:leetcode数组2道题,用时1h(有点慢)
5.LC 零矩阵(中等) 面试题 01.08. 零矩阵 - 力扣(LeetCode) 思想: 法一: 利用两个集合分别储存要清0的行和列索引 另外两种原地优化空间的做法暂时不是目前刷题目标,故不考虑 代码 c: class Solution { public:void setZeroes(vector&l…...

Javascript:数组和函数
数组 创建数组 使用new创建 let arrnew array(数组大小); 直接赋值创建 let Arr2[];let Arr3[1,A,"HELLLO"]; 这里JS的数组里面的元素属性可以各不相同 演示代码 <script>let Arr1new Array(5);let Arr2[];let Arr3[1,A,"HELLLO"];console.…...

无锁秒杀系统设计:基于Java的高效实现
引言 在电商促销活动中,秒杀场景是非常常见的。为了确保高并发下的数据一致性、性能以及用户体验,本文将介绍几种不依赖 Redis 实现的无锁秒杀方案,并提供简化后的 Java 代码示例和架构图。 一、基于数据库乐观锁机制 ✅ 实现思路…...
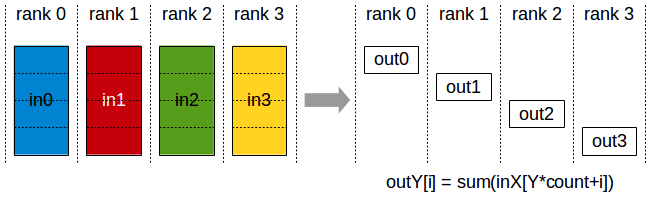
NCCL N卡通信机制
转自我的博客:https://shar-pen.github.io/2025/05/05/torch-distributed-series/nccl_communication/ from IPython.display import Image import logging import torch import torch.distributed as distpytorch 分布式相关api torch.distributed.init_process_…...

Alpha3DCS公差分析系统_国产替代的3D精度管控方案-SNK施努卡
随着智能制造发展规划的深入推进,工业软件国产化替代已上升为国家战略。在公差分析这一细分领域,长期被国外软件垄断的局面正被打破。 苏州施努卡自主研发的Alpha3DCS,凭借完全自主知识产权和军工级安全标准,成为国内实现三维公差…...
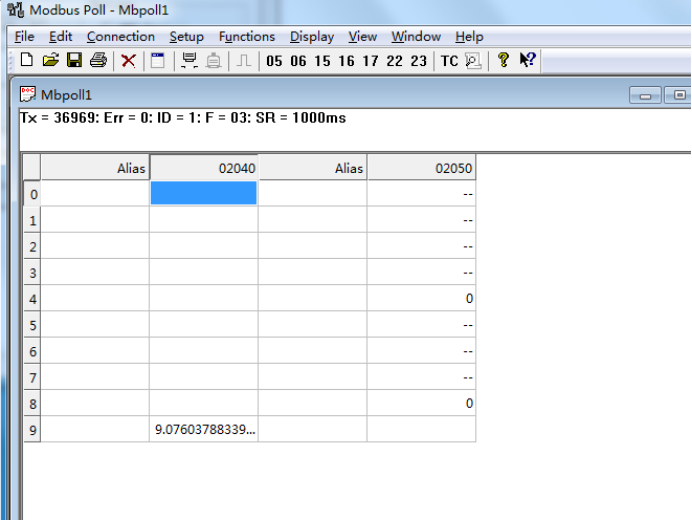
ABB电机控制和保护单元与Profibus DP主站转Modbus TCP网关快速通讯案例
ABB电机控制和保护单元与Profibus DP主站转Modbus TCP网关快速通讯案例 在现代工业自动化系统中,设备之间的互联互通至关重要。Profibus DP和Modbus TCP是两种常见的通信协议,分别应用于不同的场景。为了实现这两种协议的相互转换,Profibus …...

深入理解 Java 适配器模式:架构设计中的接口转换艺术
一、适配器模式的核心概念与设计思想 在软件开发的演进过程中,我们经常会遇到这样的场景:系统需要整合一个现有的类,但其接口与系统所需的接口不兼容。此时,适配器模式(Adapter Pattern)就成为解决接口不匹…...

skopeo工具详解
Skopeo 是一个功能强大的命令行工具,用于操作容器镜像及镜像仓库,支持多种容器镜像格式(如 Docker、OCI),能够在不下载完整镜像的情况下直接与远程仓库交互。以下是其主要功能、使用场景及操作指南: 一、核…...

vue 中的ref
vue 中的ref vue 中的ref 1. ref ** 的基本作用** 在 Vue 中,ref 是用来获取 DOM 元素或者组件实例的一种方式。对于 <el-form> 组件,通过 ref 可以获取到该表单组件的实例,进而调用表单组件提供的各种方法和访问其属性。 …...

什么是静态住宅IP?为什么静态住宅IP能提高注册通过率?
在全球最大的电商平台亚马逊上,竞争异常激烈,每一位卖家都渴望顺利通过平台的审核并成功开设店铺。在这个过程中,选择合适的IP地址成为了一个容易被忽视但至关重要的因素。静态住宅IP作为一种特殊的网络地址类型,对于提升亚马逊卖…...

数据库审计如何维护数据完整性:7 种工具和技术
在当今的数字环境中,数据库审计是维护数据完整性的一个重要方面。本文探讨了专业人员用来确保数据库系统安全性和可靠性的基本工具和技术。通过专家的独到见解,读者将发现用于监控活动、实施访问控制以及利用区块链等尖端技术进行防篡改审计的行之有效的…...

langchain 接入国内搜索api——百度AI搜索
为什么使用百度AI搜索 学习langchain的过程中,遇到使用search api的时候,发现langchain官方文档中支持的搜索工具大多是国外的,例如google search或bing search,收费不说,很多还连接不上(工具 | LangChain…...

0基础 | L298N电机驱动模块 | 使用指南
引言 在嵌入式系统开发中,电机驱动是一个常见且重要的功能。L298N是一款高电压、大电流电机驱动芯片,广泛应用于各种电机控制场景,如直流电机的正反转、调速,以及步进电机的驱动等。本文将详细介绍如何使用51单片机来控制L298N电…...

【金仓数据库征文】金仓数据库:创新驱动,引领数据库行业新未来
一、引言 在数字化转型的时代洪流中,数据已跃升为企业的核心资产,宛如企业运营与发展的 “数字命脉”。从企业日常运营的精细化管理,到战略决策的高瞻远瞩制定;从客户关系管理的深度耕耘,到供应链优化的全面协同&…...

大模型系列(五)--- GPT3: Language Models are Few-Shot Learners
论文链接: Language Models are Few-Shot Learners 点评: GPT3把参数规模扩大到1750亿,且在少样本场景下性能优异。对于所有任务,GPT-3均未进行任何梯度更新或微调,仅通过纯文本交互形式接收任务描述和少量示例。然而&…...

Qt QCheckBox 使用
1.开发背景 Qt QCheckBox 是勾选组件,具体使用方法可以参考 Qt 官方文档,这里只是记录使用过程中常用的方法示例和遇到的一些问题。 2.开发需求 QCheckBox 使用和踩坑 3.开发环境 Window10 Qt5.12.2 QtCreator4.8.2 4.功能简介 4.1 简单接口 QChec…...

Java SolonMCP 实现 MCP 实践全解析:SSE 与 STDIO 通信模式详解
一、MCP简介 MCP(Model Context Protocol,模型上下文协议)是由Anthropic公司于2024年推出的开放标准,旨在统一AI模型与外部数据源、工具之间的通信方式。MCP提供了一套规范化的接口,使大语言模型(LLM&…...

系统架构-面向服务架构(SOA)
概述 服务指的是系统对外提供的功能集 从应用的角度定义,可以认为SOA是一种应用框架,将日常业务划分为单独的业务功能和流程(即服务),SOA使用户可以构建、部署和整合这些服务。 从软件的基本原理定义,SO…...

AJAX原理
AJAX使用XHR 对象和服务器进行数据交互 XHR <p class"my-p"></p><script>const xhr new XMLHttpRequest()xhr.open(GET,http://hmajax.itheima.net/api/province)xhr.addEventListener(loadend,()>{// console.log(xhr.response)const data …...

Paddle Serving|部署一个自己的OCR识别服务器
前言 之前使用C部署了自己的OCR识别服务器,Socket网络传输部分是自己写的,回过头来一看,自己犯傻了,PaddleOCR本来就有自己的OCR服务器项目,叫PaddleServing,这里记录一下部署过程。 1 下载依赖环境 1.1 …...

Web开发—Vue工程化
文章目录 前言 Vue工程化 一、介绍 二、环境准备 1.介绍create-vue 2.NodeJS安装 3.npm介绍 三,Vue项目创建 四,项目结构 五,启动项目 六,Vue项目开发流程 七,API风格 前言 Vue工程化 前面我们在介绍Vue的时候&#…...

Word如何制作三线表格
1.需求 将像这样的表格整理成论文中需要的三线表格。 2.直观流程 选中表格 --> 表格属性中的边框与底纹B --> 在设置中选择无(重置表格)–> 确定 --> 选择第一行(其实是将第一行看成独立表格了,为了设置中线&…...

毫米波雷达点云SLAM系统
毫米波雷达点云SLAM系统 基于毫米波雷达点云数据的三维SLAM(同步定位与建图)系统,用于狭窄环境如室内和地下隧道的三维建图。 项目概述 本项目实现了一个完整的SLAM系统,利用毫米波雷达采集的点云数据进行实时定位和环境三维重建。系统特别针对狭窄空…...

5 从众效应
引言 有一个成语叫做三人成虎,意思是说,有三个人谎报市上有老虎,听者就信以为真。这种人在社会群体中,容易不加分析地接受大多数人认同的观点或行为的心理倾向,被称为从众效应。 从众效应(Bandwagon Effec…...

【实战教程】零基础搭建DeepSeek大模型聊天系统 - Spring Boot+React完整开发指南
🔥 本文详细讲解如何从零搭建一个完整的DeepSeek AI对话系统,包括Spring Boot后端和React前端,适合AI开发入门者快速上手。即使你是编程萌新,也能轻松搭建自己的AI助手! 📚博主匠心之作,强推专栏…...

用C语言实现的——一个支持完整增删查改功能的二叉排序树BST管理系统,通过控制台实现用户与数据结构的交互操作。
一、知识回顾 二叉排序树(Binary Search Tree,BST),又称二叉查找树或二叉搜索树,是一种特殊的二叉树数据结构。 基本性质: ①有序性 对于树中的每个节点,其左子树中所有节点的值都小于该节点的…...

排队论基础一:马尔可夫排队模型
排队论基础一:马尔可夫排队模型 介绍基本概念状态概率分布平均队列人数与平均排队人数平均停留时间与平均等待时间Little公式(Little Law)生灭过程生灭过程排队系统(马尔可夫排队模型)状态平衡方程介绍 最近写论文需要,学了一下排队过程模型。其实这些内容本科的时候我都…...

论文阅读笔记——ROBOGROUND: Robotic Manipulation with Grounded Vision-Language Priors
RoboGround 论文 一类中间表征是语言指令,但对于空间位置描述过于模糊(“把杯子放桌上”但不知道放桌上哪里);另一类是目标图像或点流,但是开销大;由此 GeoDEX 提出一种兼具二者的掩码。 相比于 GR-1&#…...
:架构风格总结)
系统架构设计(四):架构风格总结
黑板 概念 黑板体系架构是一种用于求解复杂问题的软件架构风格,尤其适合知识密集型、推理驱动、数据不确定性大的场景。 它模拟了人类专家协同解决问题的方式,通过一个共享的“黑板”协同多个模块(专家)逐步构建解决方案。 组…...

『 测试 』测试基础
文章目录 1. 调试与测试的区别2. 开发过程中的需求3. 开发模型3.1 软件的生命周期3.2 瀑布模型3.2.1 瀑布模型的特点/缺点 3.3 螺旋模型3.3.1 螺旋模型的特点/缺点 3.4 增量模型与迭代模型3.5 敏捷模型3.5.1 Scrum模型3.5.2 敏捷模型中的测试 4 测试模型4.1 V模型4.2 W模型(双V…...
