软件设计师-下午题-试题4(15分)

目录

1 回溯法

1.1 N皇后问题

1.1.1 非递归求解N皇后问题

1.1.2 递归求解N皇后问题

1.2 真题

2 分治法

2.1 真题

3 动态规划法

3.1 0-1背包问题

3.2 真题

---

1 回溯法

1.1 N皇后问题

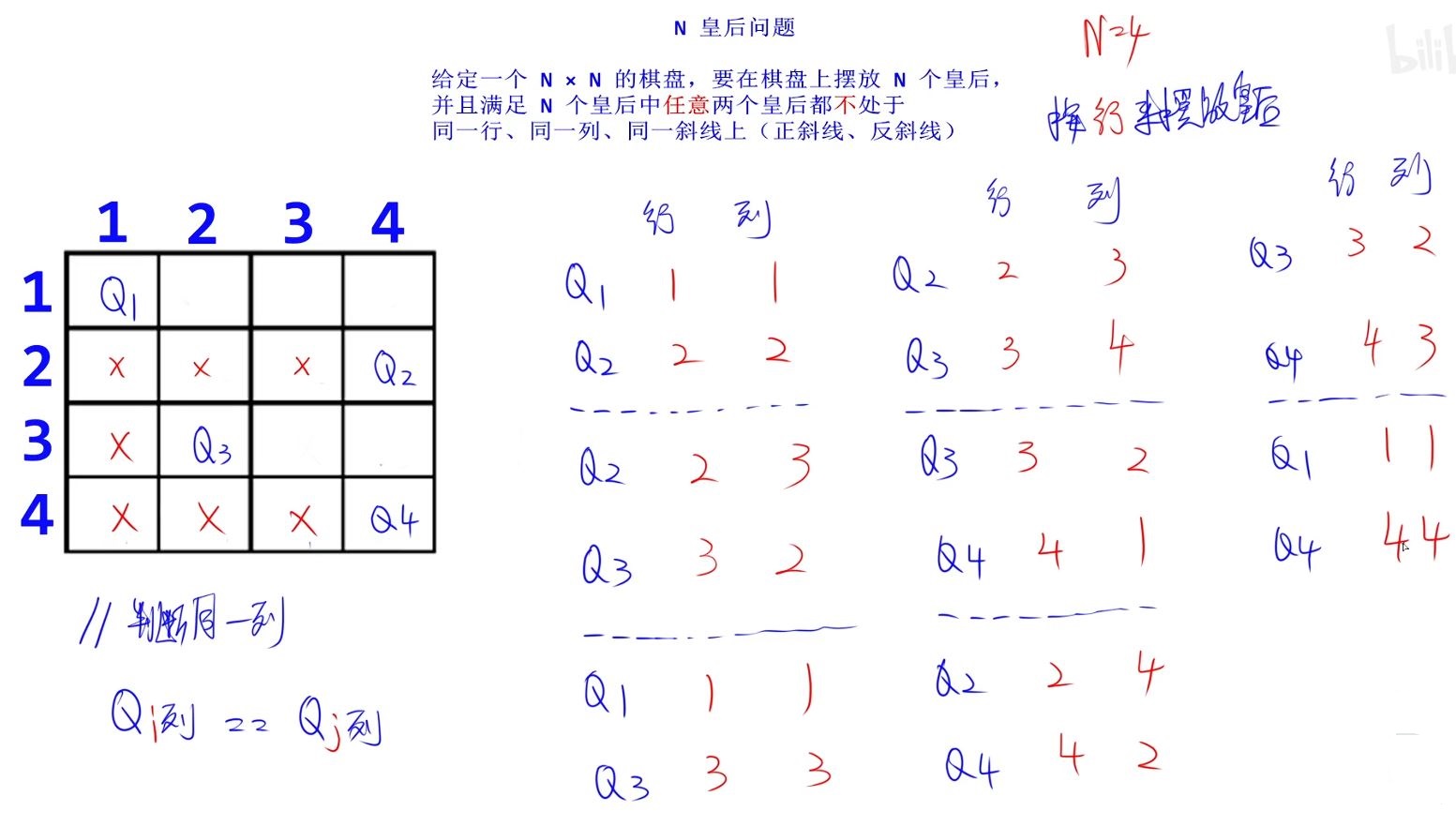
上图Q4与Q2在同一列且与Q1在同一斜线，先回溯到上一个皇后改变Q3皇后的位置，若不行，再向上回溯，直到回溯到第一个皇后位置可行，再向下回溯，直到每个皇后位置都可行。

在软考中，最终表示如下

1.1.1 非递归求解N皇后问题

#include <math.h>
#include <stdio.h>#define N 4
// #define N 10int q[N + 1]; // 存储皇后的列号int check(int j) { // 检查第 j 个皇后的位置是否合法int i;for (i = 1; i < j; i ++ ) {if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])) { // 判断是否在同一列和同一斜线上return 0;}}return 1;
}void queen() { // 求解 N 皇后 方案int i;for (i = 1; i <= N; i ++ ) {q[i] = 0;}int answer = 0; // 方案数int j = 1; // 表示正在摆放第 j 个皇后while (j >= 1) {q[j] = q[j] + 1; // 让第 j 个皇后向后一列摆放while (q[j] <= N && !check(j)) { // 判断第 j 个皇后的位置是否合法q[j] = q[j] + 1; // 不合法就往后一个位置摆放}if (q[j] <= N) { // 表示第 j 个皇后的找到一个合法的摆放位置if (j == N) { // 找到了 N 皇后的一组解answer = answer + 1;printf("方案%d：", answer);for (i = 1; i <= N; i ++ ) {printf("%d ", q[i]);}printf("\n");} else {j = j + 1; // 继续摆放下一个皇后}} else { // 表示第 j 个皇后找不到一个合法的摆放位置q[j] = 0; // 还原第 j 个皇后的位置j = j - 1; // 回溯}}
}int main() {queen();return 0;
}

1.1.2 递归求解N皇后问题

#include <math.h>
#include <stdio.h>#define N 4
// #define N 10int answer = 0;
int q[N + 1]; // 存储皇后的列号int check(int j) { // 检查第 j 个皇后的位置是否合法int i;for (i = 1; i < j; i ++ ) {if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])) { // 判断是否在同一列和同一斜线上return 0;}}return 1;
}void queen(int j) {int i;for (i = 1; i <= N; i ++ ) {q[j] = i;if (check(j)) { // 当摆放的皇后位置为合法时if (j == N) { // 找到了 N 皇后的一组解answer = answer + 1;printf("方案%d：", answer);for (i = 1; i <= N; i ++ ) {printf("%d ", q[i]);}printf("\n");} else {queen(j + 1); // 递归摆放下一个皇后的位置}}}
}int main() {queen(1);return 0;
}

1.2 真题

1.2015年上半年

2.2019年上半年

2 分治法

#include <stdio.h>
#include <sched.h>void Merge(int A[], int p, int q, int r) {int i, j, k;int L[50], R[50];int n1 = q - p + 1, n2 = r - q;for (i = 0; i < n1; i ++ ) {L[i] = A[p + i];}for (j = 0; j < n2; j ++ ) {R[j] = A[q + j + 1];}L[n1] = INT_MAX;R[n2] = INT_MAX;i = 0;j = 0;for (k = p; k < r + 1; k ++ ) {if (L[i] < R[j]) {A[k] = L[i];i ++ ;} else {A[k] = R[j];j ++ ;}}
}void MergeSort(int A[], int p, int r) {int q;if (p < r) {q = (p + r) / 2;MergeSort(A, p, q);MergeSort(A, q + 1, r);Merge(A, p, q, r);}
}int main() {int A[] = {4, 1, 3, 6, 8, 5, 2, 9};MergeSort(A, 0, 7);int i;for (i = 0; i < 8; i ++ ) {printf("%d ", A[i]);}return 0;
}

2.1 真题

1.2014年上半年

2.2017年上半年

3.2020年下半年

3 动态规划法

3.1 0-1背包问题

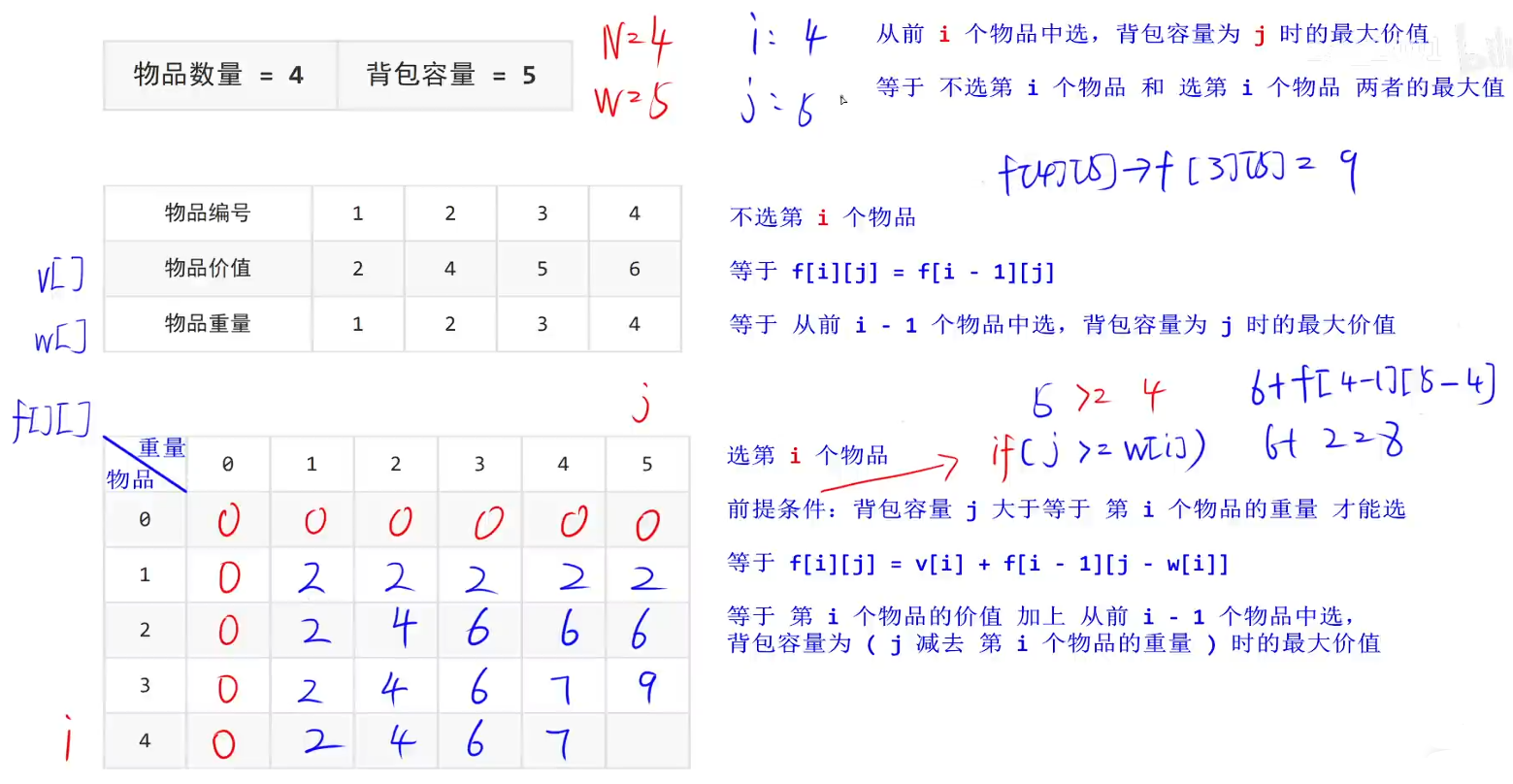
#include <stdio.h>#define N 4 // 物品数量
#define W 5 // 背包容量int max(int a, int b) {return a > b ? a : b;
}int main() {int v[] = {0, 2, 4, 5, 6}; // 物品价值数组int w[] = {0, 1, 2, 3, 4}; // 物品重量数组int f[N + 1][W + 1] = {}; // 子问题解数组int i, j;for (i = 1; i <= N; i ++ ) {for (j = 1; j <= W; j ++ ) {f[i][j] = f[i - 1][j]; // 默认不选第 i 个物品if (j >= w[i]) { // 选第 i 个物品的前提条件// 等于 不选第 i 个物品 和 选第 i 个物品 两者的较大值f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i]);}// 上方是写法 1/* ============================================================ */// 下方是写法 2 /*if (j >= w[i]) { // 选第 i 个物品的前提条件// 等于 不选第 i 个物品 和 选第 i 个物品 两者的较大值f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);} else { // 不选第 i 个物品f[i][j] = f[i - 1][j]; // 等于 从前 i - 1 个物品中选，背包容量为 j 时的最大价值}*/}}printf("%d\n", f[N][W]);for (i = 0; i <= N; i ++ ) {for (j = 0; j <= W; j ++ ) {printf("%d ", f[i][j]);}printf("\n");}return 0;
}

3.2 真题

1.2019年下半年

2.2021年下半年