数据结构与算法——链式二叉树
链式二叉树
- 遍历方式与其规则
- 代码的实现
- 递归的复习
- 前,中,后序遍历的实现
- 二叉树结点个数
- 二叉树叶子结点个数
- 二叉树第k层结点个数
- 二叉树的深度/高度
- 二叉树查找值为x的结点
- 二叉树销毁
- 层序遍历
遍历方式与其规则
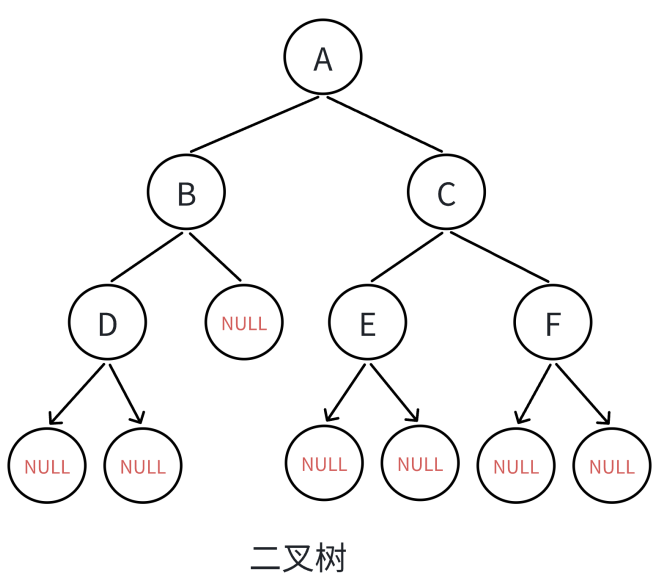
- 前序遍历:访问根结点的操作发⽣在遍历其左右⼦树之前,顺序:根,左,右
- 中序遍历:访问根结点的操作发⽣在遍历其左右⼦树之中(间),顺序:左,根,右
- 后续遍历:访问根结点的操作发⽣在遍历其左右⼦树之后,顺序:左,右,根
代码的实现
递归的复习
递归分为两个阶段,分别是递推与回归,先递推,然后回归。
定义:递归其实是⼀种解决问题的⽅法,在C语⾔中,递归就是函数自己调用自己。
思想:把⼀个⼤型复杂问题层层转化为⼀个与原问题相似,但规模较⼩的⼦问题来求解;直到⼦问题不能再被拆分,递归就结束了。所以递归的思考⽅式就是把⼤事化⼩的过程。
递归的限制条件:
- 递归存在限制条件,当满⾜这个限制条件的时候,递归便不再继续。
- 每次递归调⽤之后越来越接近这个限制条件。
前,中,后序遍历的实现
首先定义链式结构二叉树,然后自己手动构建一个如开始图中的二叉树
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//定义链式结构二叉树
typedef char BTDataType;
typedef struct BinaryTreeNode {BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//申请创建结点空间
BTNode* buyBode(char x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode)); //分配整个结构体的内存if (node == NULL){perror("malloc fail!");exit(1);}node->data = x;node->left = node->right = NULL;return node;
}
//手动创建二叉树
BTNode* creatBT()
{BTNode* nodeA = buyBode('A');BTNode* nodeB = buyBode('B');BTNode* nodeC = buyBode('C');BTNode* nodeD = buyBode('D');BTNode* nodeE = buyBode('E');BTNode* nodeF = buyBode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->left = nodeE;nodeC->right = nodeF;return nodeA;}
- 前序遍历
//前序—根左右
void preOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ",root->data);preOrder(root->left);preOrder(root->right);
}

这里画图理解一下前序遍历递归

- 中序遍历
//中序—左根右
void inOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}inOrder(root->left);printf("%c ",root->data);inOrder(root->right);
}

- 后序遍历
//后序-左右根
void postOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}inOrder(root->left);inOrder(root->right);printf("%c ", root->data);
}

二叉树结点个数
思路:根节点 + 左子树结点个数 + 右子树结点个数(需要判断根结点是否为空)
//结点个数-非空就+1
int BTNodeSize(BTNode* root)
{if (root == NULL){return 0;}return 1 + BTNodeSize(root->left) + BTNodeSize(root->right);
}


二叉树叶子结点个数
思路:如果根节点为空返回0;如果root的左结点与右结点为空,说明有且仅有root一个结点,返回1;如果都不是返回左子树叶子结点个数+右子树结点个数。
//叶子结点个数——度为0
int BTLeadSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;//有且仅有只有一个结点}return BTLeadSize(root->left) + BTLeadSize(root->right);
}


二叉树第k层结点个数
思路:左子树的第(k-1)层结点个数 + 右子树的第(k-1)层结点个数
//第k层结点个数
int BTLevelSize(BTNode* root,int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BTLevelSize(root->left, k - 1) + BTLevelSize(root->right, k - 1);
}


二叉树的深度/高度
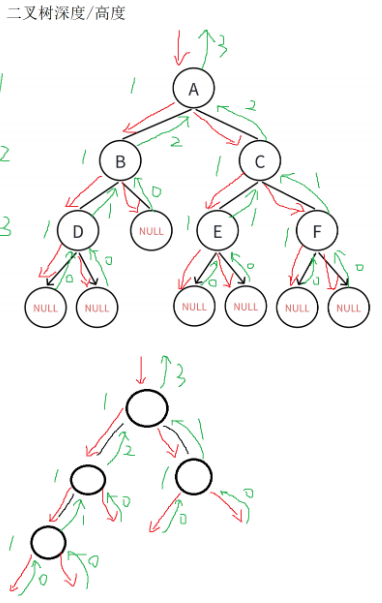
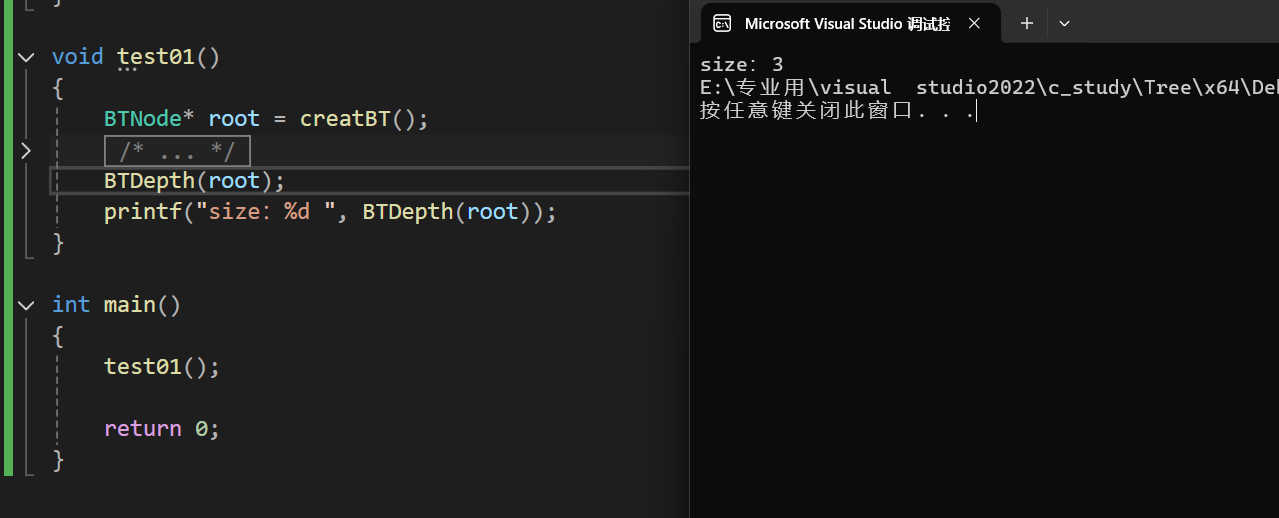
求树中结点的最大层次,根为第一次,往下递增。
思路:根结点+左子树与右子树中最大高度
//求二叉树的高度
int BTDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDep = BTDepth(root->left);int rightDep = BTDepth(root->right);return 1+(leftDep > rightDep ? leftDep : rightDep);
}
二叉树查找值为x的结点
思路:从根结点开始找,然后查找左子树,左子树查完查右子树,直到查到就返回结束,不用继续查找
//查找二叉树中的值x
BTNode* BTFind(BTNode* root, BTDataType x)
{if (root == NULL){return 0;}if (root->data == x){return root;}BTNode* leftFind = BTFind(root->left, x);if (leftFind){return leftFind;}BTNode* rightFind = BTFind(root->right, x);if (rightFind){return rightFind;}return NULL;
}

二叉树销毁
思路:结点通过遍历一个一个销毁,为了找到每一个结点,所以采用后序遍历从左子树的叶子结点往上销毁,然后从右子树的叶子结点往上销毁。
//二叉树的销毁
void BTDestroy(BTNode** root)
{if (*root == NULL){return 0;}BTDestroy(&(*root)->left);BTDestroy(&(*root)->right);free(*root);*root == NULL;
}
如果只用一级指针 BTNode* root,函数内部可以递归释放所有结点,但外部的 root 指针仍指向已被释放的内存(悬空指针),可能导致程序崩溃或未定义行为。
通过传递 BTNode** root(指针的地址),可以在释放内存后,将外部的 root 指针设为 NULL,彻底消除悬空指针。

层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对⼆叉树进⾏层序遍历。设⼆叉树的根结点所在层数为1,层序遍历就是从所在⼆叉树的根结点出发,⾸先访问第⼀层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,⾃上⽽下,⾃左⾄右逐层访问树的结点的过程就是层序遍历。
实现层序遍历需要额外借助数据结构:队列(先进先出)
队列内存储的类型是二叉树结点的结构
将结点的左右孩子入队列(前提是不为空),只要队列不为空,打印队头


/层序遍历
void leverOrder(BTNode* root)
{Q q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头,出队头BTNode* top = QueueFront(&q);QueuePop(&q);printf("%c ", top->data);//将队头非空左右孩子入队列if (top->left)QueuePush(&q, top->left);if (top->right)QueuePush(&q, top->right);}QueueDestroy(&q);
}
相关文章:

数据结构与算法——链式二叉树
链式二叉树 遍历方式与其规则代码的实现递归的复习前,中,后序遍历的实现二叉树结点个数二叉树叶子结点个数二叉树第k层结点个数二叉树的深度/高度二叉树查找值为x的结点二叉树销毁层序遍历 遍历方式与其规则 前序遍历:访问根结点的操作发⽣在…...
Android12 launcher3修改App图标白边问题
Android12 launcher3修改App图标白边问题 1.前言: 今天在Android12 Rom定制客制化系统应用时发现改变系统App图标的形状会出现一个问题,那就是图标被缩小了,没有显示完整,有一个白边,这在普通的App开发很少遇到&…...

【iOS】分类、扩展、关联对象
分类、扩展、关联对象 前言分类扩展扩展和分类的区别关联对象key的几种用法流程 总结 前言 最近的学习中笔者发现自己对于分类、扩展相关知识并不是很熟悉,刚好看源码类的加载过程中发现有类扩展与关联对象详解。本篇我们来探索一下这部分相关知识,首先…...

内蒙古工程系列建设工程技术人才评审条件
关于印发《内蒙古自治区工程系列建设工程专业技术人才职称评审条件》的通知 内蒙古工程系列建设工程技术人才评审条件适用范围 内蒙古工程系列建设工程技术人才评审条件之技术员评审要求 内蒙古工程系列建设工程技术人才评审条件之助理工程师评审要求 内蒙古工程系列建设工程技…...
)
Elasticsearch超详细安装部署教程(Windows Linux双系统)
文章目录 一、前言二、Windows系统安装部署2.1 环境准备2.2 Elasticsearch安装2.3 安装为Windows服务2.4 Head插件安装2.5 Kibana集成(可选) 三、Linux系统安装部署3.1 环境准备3.2 Elasticsearch安装3.3 系统优化3.4 启动服务3.5 安全配置(可…...

第十六章:数据治理之数据架构:数据模型和数据流转关系
本章我们说一下数据架构,说到数据架构,就很自然的想到企业架构、业务架构、软件架构,因为个人并没有对这些内容进行深入了解,所以这里不做比对是否有相似或者共通的地方,仅仅来说一下我理解的数据架构。 1、什么是架构…...

目标检测DINO-DETR(2023)详细解读
文章目录 对比去噪训练混合查询选择look forward twice 论文全称为:DETR with Improved DeNoising Anchor Boxes for End-to-End Object Detection 提出了三个新的方法: 首先,为了改进一对一的匹配效果,提出了一种对比去噪训练方法…...

基于 STM32 的蔬菜智能育苗系统硬件与软件设计
一、系统总体架构 蔬菜智能育苗系统通过单片机实时采集温湿度、光照等环境数据,根据预设阈值自动控制灌溉、补光、通风等设备,实现育苗环境的智能化管理。系统主要包括以下部分: 主控芯片:STM32F103C8T6(32 位 ARM Cortex-M3 单片机,性价比高,适合嵌入式控制)传感器模…...

实现一个带有授权码和使用时间限制的Spring Boot项目
生成和验证授权码记录授权时间和过期时间实现授权逻辑 以下是具体的实现方法: 1. 生成和验证授权码 可以使用加密技术生成和验证授权码。授权码中可以包含有效期等信息,并使用密钥进行签名。 示例代码: java复制代码 import javax.crypt…...

SGlang 推理模型优化(PD架构分离)
一、技术背景 随着大型语言模型(LLM)广泛应用于搜索、内容生成、AI助手等领域,对模型推理服务的并发能力、响应延迟和资源利用效率提出了前所未有的高要求。与模型训练相比,推理是一个持续进行、资源消耗巨大的任务,尤…...

TuyaOpen横空出世!涂鸦智能如何用开源框架重构AIoT开发范式?
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引子:AIoT开发的“不可能三角”被打破 当AI与物理世界深度融合的浪潮席卷全球,开发者们却始终面临一个“不可能三角”——开发…...
Vue语法【2】
1.插值表达式: 语法规则: {{Vue实例中data的变量名}}使用场景: 插值表达式一般使用在文本内容中,如果是元素的属性内容中则无法使用; 案例: <!DOCTYPE html> <html lang"en"> &l…...

2.2.1 05年T2
引言 本文将从一预习、二自习、三学习、四复习等四个阶段来分析2005年考研英语阅读第二篇文章。为了便于后续阅读,我将第四部分复习放在了首位。 四、复习 方法:错误思路分析总结考点文章梳理 4.1 错题分析 题目:26(细节题&…...
)
每日c/c++题 备战蓝桥杯(修理牛棚 Barn Repair)
修理牛棚 Barn Repair 题解 问题背景与挑战 在一个暴风雨交加的夜晚,Farmer John 的牛棚遭受了严重的破坏。屋顶被掀飞,大门也不翼而飞。幸运的是,许多牛正在度假,牛棚并未住满。然而,为了保护那些还在牛棚里的牛&am…...

6个月Python学习计划 Day 3
🎯 今日目标 掌握 while 和 for 循环的使用方式理解 range() 的工作机制实践:打印 1~100、累加、九九乘法表等常见程序逻辑 🧠 学习内容详解 while 循环 i 1 while i < 5:print(f"第 {i} 次循环")i 1📌 特点&…...

Linux虚拟文件系统(2)
2.3 目录项-dentry 目录项,即 dentry,用来记录文件的名字、索引节点指针以及与其他目录项的关联关系。多个关联的目录项,就构成了文件系统的目录结构。和上一章中超级块和索引节点不同,目录项并不是实际存在于磁盘上的,…...

【数据结构】栈和队列(上)
目录 一、栈(先进后出、后进先出的线性表) 1、栈的概念及结构 2、栈的底层结构分析 二、代码实现 1、定义一个栈 2、栈的初始化 3、入栈 3、增容 4、出栈 5、取栈顶 6、销毁栈 一、栈(先进后出、后进先出的线性表) 1、…...

科技赋能·长效治理|无忧树建筑修缮渗漏水长效治理交流会圆满举行!
聚焦行业痛点,共话长效未来!5月16日,由无忧树主办的主题为“科技赋能长效治理”的建筑修缮渗漏水长效治理技术交流会在上海圆满举行。来自全国的建筑企业代表、专家学者、技术精英齐聚一堂,共探渗漏治理前沿技术,见证科…...

【闲聊篇】java好丰富!
1、在学习mybatis-plus的文档时,发现引入了solon依赖,才发现这是一个对标spring生态的框架,有意思! 还有若依框架,真的好丰富~~~~~~~ 2、今天面试官问我,他说很少遇到用redission做延迟队列的。后面我就反…...

STL中list的模拟
这里写目录标题 list 的节点 —— ListNodelist 的 “导览员” —— ListIteratorlist 的核心 —— list 类构造函数迭代器相关操作容量相关操作 结尾 在 C 的 STL(标准模板库)中,list 是一个十分重要的容器,它就像一个灵活的弹簧…...

6.3.2图的深度优先遍历
知识总览: 树的先根遍历: 采用递归一直找某个节点的子树直到找不到从上往下找 访问根节点1,1的子树有2、3、4,访问2,2节点子树有5访问5,5没有子树,退回到2,2还有子树6访问6,6没有子树再退回到2,2的子树都被访问了再退…...

畅游Diffusion数字人(30):情绪化数字人视频生成
畅游Diffusion数字人(0):专栏文章导航 前言:仅从音频生成此类运动极具挑战性,因为它在音频和运动之间存在一对多的相关性。运动视频的情绪是多元化的选择,之前的工作很少考虑情绪化的数字人生成。今天解读一个最新的工作FLOAT,可以生成制定情绪化的数字人视频。 目录 贡献…...

UE5 Va Res发送请求、处理请求、json使用
文章目录 介绍发送一个Get请求发送Post请求设置请求头请求体带添json发送请求完整的发送蓝图 处理收到的数据常用的json处理节点 介绍 UE5 自带的Http插件,插件内自带json解析功能 发送一个Get请求 只能写在事件图表里 发送Post请求 只能写在事件图表里 设置…...
.openEndDrawer();不生效问题)
关于flutter中Scaffold.of(context).openEndDrawer();不生效问题
原因: 在 Flutter 中,Scaffold.of(context) 会沿着当前的 context 向上查找最近的 Scaffold。如果当前的 widget 树层级中没有合适的 Scaffold(比如按钮所在的 context 是在某个子 widget 中),就找不到它。 解决办法…...

【C++】深入理解C++中的函数与运算符重载
文章目录 前言一、什么是重载?1.1 函数重载1.1.1 函数重载的规则1.1.2 示例:函数重载 1.2 运算符重载1.2.1 运算符重载的规则1.2.2 示例:运算符重载 1.2.3 运算符重载的注意事项 二、重载的注意事项2.1 重载的二义性2.2 默认参数和重载2.3 运…...
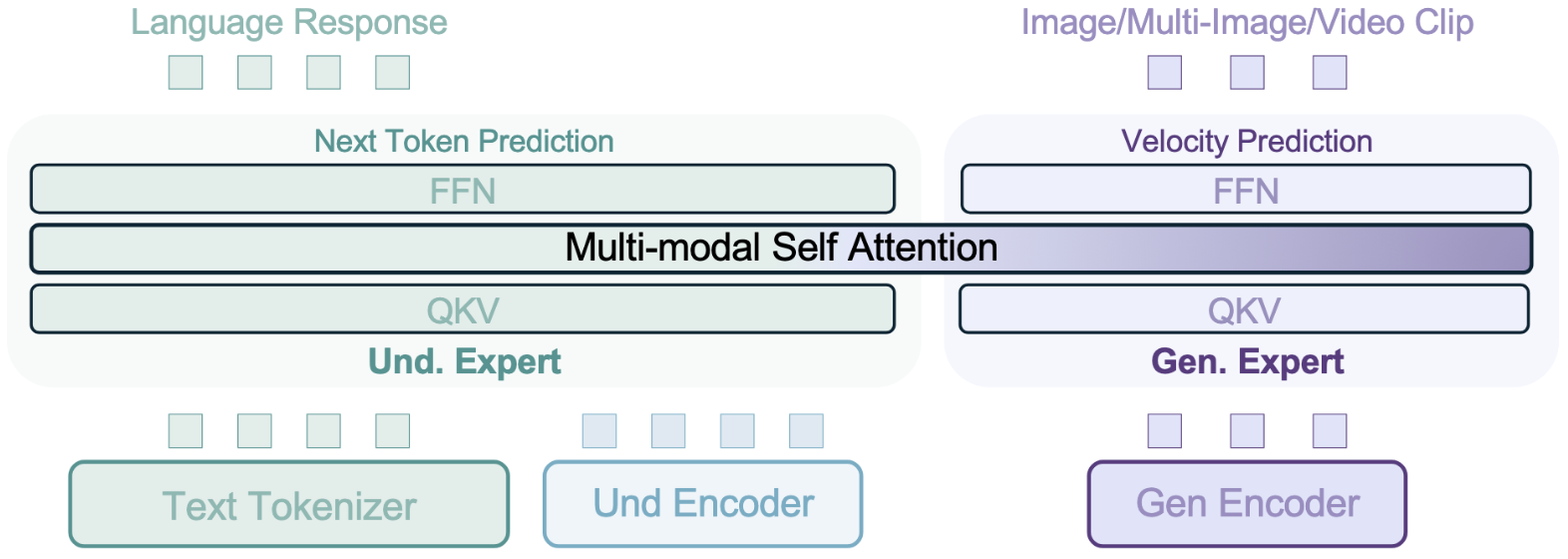
【读代码】BAGEL:统一多模态理解与生成的模型
一、项目概览 1.1 核心定位 BAGEL是字节跳动推出的开源多模态基础模型,具有70亿激活参数(140亿总参数)。该模型在统一架构下实现了三大核心能力: 多模态理解:在MME、MMBench等9大评测基准中超越Qwen2.5-VL等主流模型文本生成图像:生成质量媲美SD3等专业生成模型智能图像…...

隧道自动化监测解决方案
行业现状 隧道作为一种重要的交通运输通道,不管是缓解交通压力,还是让路网结构更趋于完善,它都有着不可估量的作用。隧道在运营过程中,由于受到材料退化、地震、人为因素等影响会发生隧道主体结构的损坏和劣化。若不及时检修和维护…...

如何通过EventChannel实现Flutter与原生平台的双向通信?
在Flutter开发中,EventChannel是处理单向数据流的核心组件,尤其适用于原生平台(Android/iOS)主动向Flutter端推送实时数据的场景,例如传感器数据、后台任务通知等。虽然EventChannel本身以原生到Flutter的单向通信为主,但结合特定设计模式,仍可实现双向交互。本文将详细…...

游戏引擎学习第307天:排序组可视化
简短谈谈直播编程的一些好处。 上次结束后,很多人都指出代码中存在一个拼写错误,因此这次我们一开始就知道有一个 bug 等待修复,省去了调试寻找错误的时间。 今天的任务就是修复这个已知 bug,然后继续排查其他潜在的问题。如果短…...

java接口自动化初识
简介 了解什么是接口和为什么要做接口测试。并且知道接口自动化测试应该学习哪些技术以及接口自动化测试的落地过程。 一、什么是接口 在这里我举了一个比较生活化的例子,比如我们有一台笔记本,在笔记本的两端有很多插口。例如:USB插口。那…...
