OpenSSL 与 C++ 搭建一个支持 TLS 1.3 的服务器
好的,我们可以使用 OpenSSL 与 C++ 搭建一个支持 TLS 1.3 的服务器。下面是:
✅ 一、完整示例代码(基于 OpenSSL)
使用 C++ 和 OpenSSL 创建一个简单的 TCP TLS 服务器,支持 TLS 1.3。
✅ 代码:tls_server.cpp
#include <openssl/ssl.h>
#include <openssl/err.h>
#include <arpa/inet.h>
#include <unistd.h>
#include <iostream>#define PORT 4433void init_openssl() {SSL_load_error_strings();OpenSSL_add_ssl_algorithms();
}void cleanup_openssl() {EVP_cleanup();
}SSL_CTX* create_context() {// 1️⃣ 明确使用 TLS 服务器方法(会自动支持 TLS 1.3)const SSL_METHOD* method = TLS_server_method();SSL_CTX* ctx = SSL_CTX_new(method);if (!ctx) {ERR_print_errors_fp(stderr);exit(EXIT_FAILURE);}// 2️⃣ 可选:强制只允许 TLS 1.3(如果不加,OpenSSL 会使用 TLS1.2+)SSL_CTX_set_min_proto_version(ctx, TLS1_3_VERSION);SSL_CTX_set_max_proto_version(ctx, TLS1_3_VERSION);return ctx;
}void configure_context(SSL_CTX* ctx) {// 加载证书和私钥if (SSL_CTX_use_certificate_file(ctx, "cert.pem", SSL_FILETYPE_PEM) <= 0 ||SSL_CTX_use_PrivateKey_file(ctx, "key.pem", SSL_FILETYPE_PEM) <= 0) {ERR_print_errors_fp(stderr);exit(EXIT_FAILURE);}
}int main() {init_openssl();SSL_CTX* ctx = create_context();configure_context(ctx);int sock = socket(AF_INET, SOCK_STREAM, 0);sockaddr_in addr;addr.sin_family = AF_INET;addr.sin_port = htons(PORT);addr.sin_addr.s_addr = INADDR_ANY;bind(sock, (struct sockaddr*)&addr, sizeof(addr));listen(sock, 1);std::cout << "TLS server listening on port " << PORT << std::endl;while (1) {struct sockaddr_in client_addr;uint32_t len = sizeof(client_addr);int client = accept(sock, (struct sockaddr*)&client_addr, &len);SSL* ssl = SSL_new(ctx);SSL_set_fd(ssl, client);if (SSL_accept(ssl) <= 0) {ERR_print_errors_fp(stderr);} else {const char reply[] = "Hello over TLS 1.3!\n";SSL_write(ssl, reply, strlen(reply));}SSL_shutdown(ssl);SSL_free(ssl);close(client);}close(sock);SSL_CTX_free(ctx);cleanup_openssl();return 0;
}
📌 二、在哪里决定是否支持 TLS 1.3?
关键代码如下:
// 决定允许的最小和最大 TLS 版本
SSL_CTX_set_min_proto_version(ctx, TLS1_3_VERSION);
SSL_CTX_set_max_proto_version(ctx, TLS1_3_VERSION);
这两行代码强制只使用 TLS 1.3。
如果你想支持多个版本(比如 TLS 1.2 和 1.3),可以改成:
SSL_CTX_set_min_proto_version(ctx, TLS1_2_VERSION);
SSL_CTX_set_max_proto_version(ctx, TLS1_3_VERSION);
✅ 三、编译方法
你需要先安装 OpenSSL 开发库(通常是 libssl-dev):
sudo apt-get install libssl-dev
然后使用 g++ 编译:
g++ tls_server.cpp -o tls_server -lssl -lcrypto
✅ 四、测试方法
你可以使用 openssl s_client 模拟客户端:
openssl s_client -connect localhost:4433 -tls1_3
如果一切正常,会看到握手成功并打印证书信息。
如果你需要支持多客户端或使用异步 IO(如 epoll),可以进一步封装;这个示例是最小可运行 TLS 1.3 服务器。如果你想部署到生产,建议使用更安全的证书管理和错误处理机制。
是否需要我给你生成 cert.pem 和 key.pem 的命令?
相关文章:

OpenSSL 与 C++ 搭建一个支持 TLS 1.3 的服务器
好的,我们可以使用 OpenSSL 与 C 搭建一个支持 TLS 1.3 的服务器。下面是: ✅ 一、完整示例代码(基于 OpenSSL) 使用 C 和 OpenSSL 创建一个简单的 TCP TLS 服务器,支持 TLS 1.3。 ✅ 代码:tls_server.cp…...
)
HOW - 简历和求职面试宝典(六)
文章目录 1. 如何更好地认识自己?一、认清自己的实力二、明确求职方向三、认识求职岗位与自己的匹配度2. 如何判断公司是否合适自己?一、网站平台二、内部人员三、通过面试官1. 如何更好地认识自己? 一、认清自己的实力 我们经常会听到这样的话:我现在的工作做的好不开心…...

【机器学习基础】机器学习入门核心算法:逻辑回归(Logistic Regression)
机器学习入门核心算法:逻辑回归(Logistic Regression) 一、算法逻辑1.1 基本概念1.2 Sigmoid函数1.3 决策边界 二、算法原理与数学推导2.1 概率建模2.2 损失函数推导2.3 梯度下降优化2.4 正则化处理 三、模型评估3.1 常用评估指标3.2 ROC曲线…...

深入理解设计模式之命令模式
下面是一篇关于设计模式之命令模式(Command Pattern)的详细博客,并附有 Java 实现代码示例。 深入理解设计模式之:命令模式(Command Pattern) 一、什么是命令模式? 命令模式(Comma…...

智能仓储落地:机器人如何通过自动化减少仓库操作失误?
仓库作业的速度和准确性至关重要,尤其是在当前对无差错、高效作业的要求达到前所未有的环境下。每一个错误,无论是物品放错位置还是库存差异,都会在供应链中产生连锁反应,造成延误、增加成本,并最终影响客户满意度。 …...

Android 架构演进之路:从 MVC 到 MVI,拥抱单向数据流的革命
在移动应用开发的世界里,架构模式的演进从未停歇。从早期的 MVC 到后来的 MVP、MVVM,每一次变革都在尝试解决前一代架构的痛点。而今天,我们将探讨一种全新的架构模式 ——MVI(Model-View-Intent),它借鉴了…...

[低代码表单生成器设计基础]ElementUI中Layout布局属性Form表单属性详解
Layout 布局 ElementUI 的 Layout 布局系统基于 24 栏栅格设计,提供了灵活的响应式布局能力,适用于各种页面结构的构建。(CSDN) 📐 基础布局结构 ElementUI 的布局由 <el-row>(行)和 <el-col>࿰…...

数据结构7——二叉树
一、二叉树的定义与性质 1.定义 首先是树形结构,每个节点最多有2棵树,二叉树的子树有左右之分,不能颠倒。 2.性质 (1)二叉树的第i层,最多有2的(i-1)次幂。 (2)深度为k࿰…...

从“被动养老”到“主动健康管理”:平台如何重构代际关系?
在老龄化与数字化交织的背景下,代际关系的重构已成为破解养老难题的关键。 传统家庭养老模式中,代际互动多表现为单向的“赡养-被赡养”关系。 而智慧养老平台的介入,通过技术赋能、资源整合与情感连接,正在推动代际关系向“协作…...

Java 中的 synchronized 和 Lock:如何保证线程安全
Java 中的 synchronized 和 Lock:如何保证线程安全 引言 在 Java 多线程编程中,线程安全是一个核心问题。当多个线程同时访问共享资源时,可能会导致数据不一致或其他不可预期的结果。synchronized关键字和Lock接口是 Java 中实现线程同步的…...

贪心算法应用:最大匹配问题详解
Java中的贪心算法应用:最大匹配问题详解 贪心算法是一种在每一步选择中都采取当前状态下最优的选择,从而希望导致结果是全局最优的算法策略。在Java中,贪心算法可以应用于多种问题,其中最大匹配问题是一个经典的应用场景。下面我将从基础概念到具体实现,全面详细地讲解贪…...

爬虫IP代理效率优化:策略解析与实战案例
目录 一、代理池效率瓶颈的根源分析 二、六大核心优化策略 策略1:智能IP轮换矩阵 策略2:连接复用优化 策略3:动态指纹伪装 策略4:智能重试机制 三、典型场景实战案例 案例1:电商价格监控系统 案例2:…...

豆瓣电视剧数据工程实践:从爬虫到智能存储的技术演进(含完整代码)
通过网盘分享的文件:资料 链接: https://pan.baidu.com/s/1siOrGmM4n-m3jv95OCea9g?pwd4jir 提取码: 4jir 1. 引言 1.1 选题背景 在影视内容消费升级背景下,豆瓣电视剧榜单作为国内最具影响力的影视评价体系,其数据价值体现在:…...
的漏洞特征流量特征)
【HW系列】—C2远控服务器(webshell链接工具, metasploit、cobaltstrike)的漏洞特征流量特征
文章目录 蚁剑、冰蝎、哥斯拉一、蚁剑(AntSword)流量特征二、冰蝎(Behinder)流量特征三、哥斯拉(Godzilla)流量特征 metasploit、cobaltstrike一、Metasploit流量特征二、CobaltStrike流量特征三、检测与防…...

5.28 孔老师 nlp讲座
本次讲座主要介绍了语言模型的起源、预训练模型以及大语言模型(需要闫老师后讲)等内容。首先,语言模型的起源可以追溯到语音识别中的统计语言模型,通过估计声学参数串产生文字串的概率来找到最大概率的文字串。然后,介…...

基于微信小程序的漫展系统的设计与实现
博主介绍:java高级开发,从事互联网行业六年,熟悉各种主流语言,精通java、python、php、爬虫、web开发,已经做了六年的毕业设计程序开发,开发过上千套毕业设计程序,没有什么华丽的语言࿰…...

打卡day39
一、 图像数据的介绍 1.1 灰度图像 # 先继续之前的代码 import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader , Dataset # DataLoader 是 PyTorch 中用于加载数据的工具 from torchvision import datasets, transforms…...

基于Web的分布式图集管理系统架构设计与实践
引言:为什么需要分布式图集管理? 在现代Web图形应用中,纹理图集(Texture Atlas)技术是优化渲染性能的关键手段。传统的图集制作流程通常需要美术人员使用专业工具(如TexturePacker)离线制作&am…...

mysql执行sql语句报错事务锁住
报错情况 1205 - Lock wait timeout exceeded; try restarting transaction先找出长时间运行的事务 SELECT * FROM information_schema.INNODB_TRX ORDER BY trx_started ASC;终止长时间运行的事务 KILL [PROCESS_ID];...

Java消息队列应用:Kafka、RabbitMQ选择与优化
Java消息队列应用:Kafka、RabbitMQ选择与优化 在Java应用领域,消息队列是实现异步通信、应用解耦、流量削峰等重要功能的关键组件。Kafka和RabbitMQ作为两种主流的消息队列技术,各有特点和适用场景。本文将深入探讨Kafka和RabbitMQ在Java中的…...

零基础设计模式——结构型模式 - 组合模式
第三部分:结构型模式 - 组合模式 (Composite Pattern) 在学习了桥接模式如何分离抽象和实现以应对多维度变化后,我们来探讨组合模式。组合模式允许你将对象组合成树形结构来表现“整体-部分”的层次结构。组合模式使得用户对单个对象和组合对象的使用具…...

额度年审领域知识讲解
金融领域的“额度年审”是一个非常重要的常规性工作。它指的是金融机构(主要是银行)对其授予客户的各种信用额度或授信额度,在授信有效期内(通常是一年)进行周期性的重新评估、审查和确认的过程。 核心目的࿱…...

腾讯云国际站可靠性测试
在数字化转型加速的今天,企业对于云服务的依赖已从“可选”变为“必需”。无论是跨境电商的实时交易,还是跨国企业的数据协同,云服务的可靠性直接决定了业务连续性。作为中国领先的云服务提供商,腾讯云国际站(Tencent …...

自定义异常小练习
在开始之前,让我们高喊我们的口号: 键盘敲烂,年薪百万! 目录 键盘敲烂,年薪百万! 异常综合练习: 自定义异常 异常综合练习: 自定义异常: 定义异常类写继承关系空参构造带参构造 自定…...

SpringBoot整合MinIO实现文件上传
使用Spring Boot与JSP和MinIO(一个开源对象存储系统,兼容Amazon S3)进行集成,您可以创建一个Web应用来上传、存储和管理文件。以下是如何将Spring Boot、JSP和MinIO集成的基本步骤: 这个是minio正确启动界面 这个是min…...

基于面向对象设计的C++日期推算引擎:精准高效的时间运算实现与运算重载工程化实践
前引: 在软件开发中,时间与日期的处理是基础但极具挑战性的任务。传统的手工日期运算逻辑往往面临闰年规则、月份天数动态变化、时区转换等复杂场景的容错难题,且代码冗余度高、可维护性差。本文将深入探讨如何利用C的面向对象特性与成员函数…...
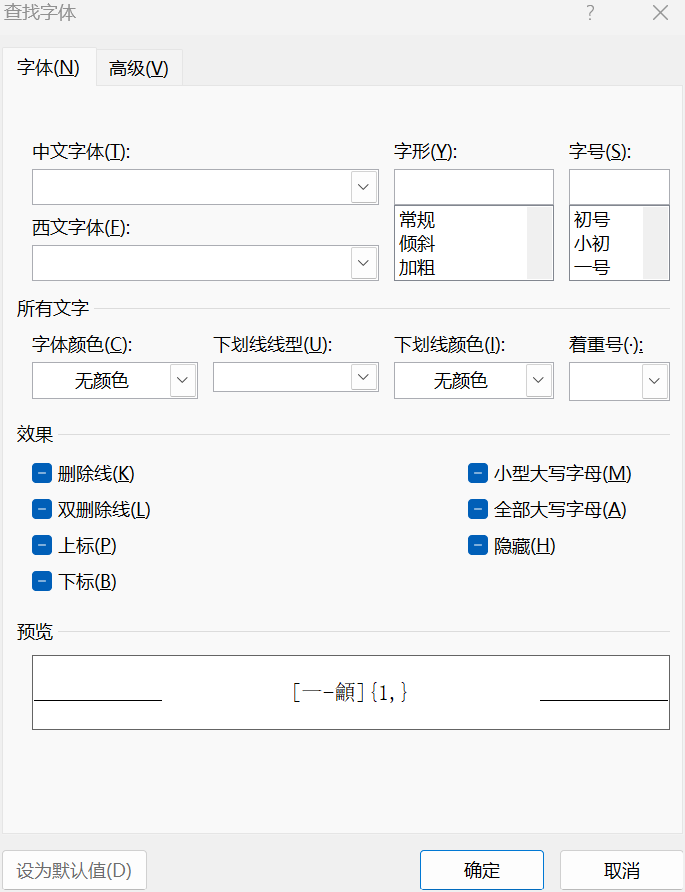
如何把 Microsoft Word 中所有的汉字字体替换为宋体?
Ctrl H ,然后,点击更多,勾选使用通配符,查找内容中填入 [一-龥]{1,}, 这是 Word 通配符匹配汉字的经典写法(匹配 Unicode 范围内的 CJK 汉字)。 然后, “替换为”留空,点…...
02. [Python+Golang+PHP]三数之和,多种语言实现最优解demo
一、问题描述:三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。 注意:答案中…...

MongoDB选择理由
1.简介 MongoDB是一个基于分布式文件存储的数据库由C语言编写,旨在为WEB应用提供可扩展的高性能数据存储解决方案。MongoDB是一个介于关系数据库和非关系数据库之间的产品,是非关系数据库当中功能最丰富,最像关系数据库的。Mongo最大的特点是…...

倚光科技在二元衍射面加工技术上的革新:引领光学元件制造新方向
倚光科技二元衍射面加工技术(呈现出细腻的光碟反射纹路) 在光学元件制造领域,二元衍射面的加工技术一直是行业发展的关键驱动力之一。其精准的光相位调制能力,在诸多前沿光学应用中扮演着不可或缺的角色。然而,长期以来…...
