ch12 课堂参考代码 及 题目参考思路
课堂参考代码
Bellman-Ford
主要思路:对所有的边进行 n-1 轮松弛操作
单源最短路算法, O ( n m ) O(nm) O(nm)
using ll = long long;
const int maxn = 5010, maxm = 5010;
struct Edge {int u, v, w;
} E[maxm];
// d[u]: 当前 s 到 u 的最短路
ll d[maxn];
int n, m;
bool Bf(int s) {memset(d, 0x3f, sizeof(d));d[s] = 0;for (int i = 0; i < n - 1; ++i) {// 使用每条边进行松弛操作for (int j = 0; j < m; ++j) {int u = E[j].u, v = E[j].v, w = E[j].w;d[v] = min(d[v], d[u] + w);}}for (int j = 0; j < m; ++j) {int u = E[j].u, v = E[j].v, w = E[j].w;if (d[v] > d[u] + w) return 1; // 存在负环}return 0;// 判断负环:做一次以每条边进行松弛操作,如果还能松弛成功就是负环// 注意,如果还能松弛成功是图中存在负环,不是存在从 s 出发能到达的负环
}
int main() {cin >> n >> m;for (int i = 0; i < m; ++i) {cin >> E[i].u >> E[i].v >> E[i].w;}Bf(1);// ... return 0;
}
SPFA
Bellman-ford 算法的队列优化
主要思路:使用每条边进行更新。一个点被更新过才用它的出边进行更新其它点的最短路
单源最短路算法
随机图上平均复杂度 O ( k m ) O(km) O(km), k k k 为每个点的平均进队次数 (一般的,k是一个常数,在稀疏图中小于2)
最坏复杂度与 Bellman-Ford 算法相同, O ( n m ) O(nm) O(nm)
using ll = long long;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int maxn = 5010, maxm = 5010;
struct edge {int v, w;
};
vector<edge> G[maxn];
// d[u]: 当前 u 的最短路
ll d[maxn];
int n;
bool inq[maxn];
// cnt: 记录最短路上的路径数
int cnt[maxn];
bool spfa(int s) {memset(d, 0x3f, sizeof(d));memset(inq, 0, sizeof(inq));queue<int> q;// 把源点 s 入队d[s] = 0, cnt[s] = 0, q.push(s), inq[s] = 1;while (!q.empty()) {int u = q.front();q.pop(), inq[u] = 0;for (int i = 0; i < G[u].size(); i++) {int v = G[u][i].v, w = G[u][i].w;// 如果松弛操作成功才入队if (d[v] > d[u] + w) {d[v] = d[u] + w;// v 的最短路上路径数为 u 最短路上路径数 + 1cnt[v] = cnt[u] + 1;if (cnt[v] >= n) return 1; // 存在负环// 保证不会重复出现在队列if (!inq[v]) {q.push(v), inq[v] = 1;}}}}return 0;
}
int main() {// s 为单源最短路的源点int m, u, v, w, s = 1;cin >> n >> m;for (int i = 0; i < m; ++i) {cin >> u >> v >> w;G[u].push_back({v, w});// 注意看题目是否是双向边}spfa(1);// ...return 0;
}
Floyd-Warshall
多源最短路算法, O ( n 3 ) O(n^3) O(n3)
using ll = long long;
const int maxn = 410;
ll d[maxn][maxn];
int main() {int n;cin >> n;for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {cin >> d[i][j];}}for (int k = 1; k <= n; ++k) {for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}// ...return 0;
}
总结
- 单源最短路算法
- Dijkstra:适用于边权非负的图,时间复杂度 O ( m log m ) O(m\log m) O(mlogm)
- Bellman-Ford:可用于任意图,能判断负环,时间复杂度 O ( n m ) O(nm) O(nm) ,一般不用,直接用 SPFA
- SPFA:适用范围与 Bellman-Ford 相同,随机图效率很高,但最坏复杂度 O ( n m ) O(nm) O(nm)
- 全局最短路算法
- Floyd:可用于任意图,能判断负环,时间复杂度 O ( n 3 ) O(n^3) O(n3)
ch12 部分题目解法
炼金术士小图 II
-
分析:
- 这里处理技巧与 ch10 章节中题目 【Watering Hole】中的类似,考虑设定一个超级源点,编号记为 n+1
- n 种材料看作 n 个结点,再加一个编号为 n + 1 的结点表示起点(什么材料都没有),花费作为边权,问题转换为从起点到结点 n 的单源最短路问题
- 建图
- 从起点 n + 1 向代表材料的每个结点 i 连一条边权为 p i p_i pi 的有向边,表示可以花费 p i p_i pi 从“什么都没有”到“拥有材料 i”。
- 对于 type = 1 类型的转化,从结点 a i a_i ai 向 b i b_i bi 连一条边权为 c i c_i ci 的有向边。
- 对于 type = 2 类型的分解,从结点 a i a_i ai 向 b i b_i bi 连一条边权为 − c i -c_i −ci 的有向边。(花费 − c i -c_i −ci 就表示赚取 c i c_i ci)
- 跑 SPFA 求从起点 n + 1 到 n 的最短路。
- 如果存在负环,说明可以赚取无限的利润。
- 如果 d[n] < 0 ,说明得到材料 n 花费负数费用,即赚取了利润。
- 注意整个图有 n + 1 个结点,负环的判断应该是存在边数 >= n+1 的最短路,而不是 >= n。(写 >= n 也不会出错,因为起点只有出边没有入边,不会在环中)
-
代码
int main() {int m, pi;cin >> n >> m;// 每个点都和 n+1 节点相连for (int i = 1; i <= n; i++) {cin >> pi;G[n + 1].push_back({i, pi});}for (int i = 1; i <= m; i++) {int t, a, b, c;cin >> t >> a >> b >> c;if (t == 1)G[a].push_back({b, c});elseG[a].push_back({b, -c});}// 从 n + 1 节点出发跑 spfa 算法// 计算到达 n 号节点的最短路长度bool flag = spfa(n + 1);if (flag || d[n] < 0) // 有负环 或 到 n 的最短路为负则存在利润cout << "lucky" << endl;elsecout << d[n] << endl;return 0; }路况查询
-
分析:
-
因为查询次数 q 较大,如果对于每次查询都去跑一次单源最短路,时间复杂度较高。
-
本题是对于 Floyd 原理的应用。允许经过结点 k 时,Floyd 算法执行了以下代码
for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {f[i][j] = min(f[i][j], f[i][k] + f[k][j]);} }那么城市 x 解封时,表示允许经过结点 x ,将以上代码 k 改为 x 执行一遍即可。
-
对于 type = 2 类型的询问
- 先判断 x 和 y 的解封情况,可以通过 bool 数组标记和判断。
- x 或 y 还未解封, 或 f[x][y] == 正无穷大,说明无法到达。
- 否则输出 f[x][y] 。
-
-
代码:详见课本【例12.4】路况查询
Cow Hurdles
-
分析:
-
最短路问题是希望路径边权之和最小,本题希望路径中的最大边权最小,只需要修改松弛操作即可。
-
从数据范围看出如果每次询问跑一遍单源最短路,效率较低,用 Floyd 算法比较合适。
-
f[i][j] 原本表示 i 到 j 的路径中,最小的路径长度,改为表示 i 到 j 的路径中,最小的最大边权。
-
将 Floyd 的状态转移从
f[i][j] = min(f[i][j], f[i][k] + f[k][j])改为
f[i][j] = min(f[i][j], max(f[i][k], f[k][j]))即可
f[i][k] + f[k][j]表示经过 k 的路径中 i 到 j 的最短路长度,求路径总长度所以用加法。max(f[i][k], f[k][j])是从经过 k 的路径中 i 到 j 的最大边权。
-
最后如果 f[a][b] == 正无穷大,表示无法从 a 到达 b,输出 -1,否则输出 f[a][b] 。
-
-
代码:详见课本【例12.3】跳跃比赛
相关文章:

ch12 课堂参考代码 及 题目参考思路
课堂参考代码 Bellman-Ford 主要思路:对所有的边进行 n-1 轮松弛操作 单源最短路算法, O ( n m ) O(nm) O(nm) using ll long long; const int maxn 5010, maxm 5010; struct Edge {int u, v, w; } E[maxm]; // d[u]: 当前 s 到 u 的最短路 ll d[m…...

uniapp 实现腾讯云 IM 消息已读回执
uniapp 实现腾讯云 IM 消息已读回执处理全攻略 一、功能实现原理 腾讯云 IM 的已读回执功能通过 消息已读上报机制 实现,核心流程如下: 接收方阅读消息时,客户端自动上报已读状态云端记录最新已读时间戳(精确到会话维度&#x…...

JavaScript 性能优化按层次逐步分析
JavaScript 性能优化实战 💡 本文数据基于Chrome 136实测验证,涵盖12项核心优化指标,通过20代码案例演示性能提升300%的实战技巧。 一、代码层深度优化 1. 高效数据操作(百万级数据处理) // 不良实践:频繁…...
)
三分钟打通Stable Diffusion提示词(附实战手册)
文章目录 一、提示词的本质是"思维翻译器"避坑指南1:三大常见翻车现场 二、结构化提示词公式(抄作业版)实战案例:生成赛博朋克猫咪 三、进阶玩家的秘密武器1. 权重控制大法2. 风格融合黑科技3. 时间轴控制 四、避不开的…...

【Linux网络篇】:初步理解应用层协议以及何为序列化和反序列化
✨感谢您阅读本篇文章,文章内容是个人学习笔记的整理,如果哪里有误的话还请您指正噢✨ ✨ 个人主页:余辉zmh–CSDN博客 ✨ 文章所属专栏:Linux篇–CSDN博客 文章目录 一.序列化和反序列化为什么需要序列化和反序列化为什么应用层…...

RK3588 Opencv-ffmpeg-rkmpp-rkrga编译与测试
RK3588 Opencv-ffmpeg-rkmpp-rkrga编译与测试 硬件背景说明编译环境准备1. 编译MPP(媒体处理平台)2. 编译RGA(图形加速库)3. 构建支持硬件加速的FFmpeg重要代码修改说明4. 验证安装5.FFmpeg转码测试OpenCV编译集成Python OpenCV+FFmpeg测试硬件背景说明 RK3588是瑞芯微推出…...

特伦斯 S75 电钢琴:奏响极致音乐体验的华丽乐章
在音乐爱好者增多、音乐教育普及,以及科技进步的推动下,电钢琴市场蓬勃发展。其在技术、品质和应用场景上变化巨大,高端化、个性化产品受青睐,应用场景愈发多元。在此背景下,特伦斯 S75 电钢琴以卓越性能和独特设计&am…...

硬件学习笔记--64 MCU的ARM核架构发展及特点
MCU(微控制器)的ARM核架构是当前嵌入式系统的主流选择,其基于ARM Cortex-M系列处理器内核,具有高性能、低功耗、丰富外设支持等特点。以下是ARM核MCU的主要架构及其发展: 1. ARM Cortex-M系列内核概览 ARM Cortex-M系…...

div或button一些好看实用的 CSS 样式示例
1:现代渐变按钮 .count {width: 800px;background: linear-gradient(135deg, #72EDF2 0%, #5151E5 100%);padding: 12px 24px;border-radius: 10px;box-shadow: 0 4px 15px rgba(81, 81, 229, 0.3);color: white;font-weight: bold;border: none;cursor: pointer;t…...

USB充电检测仪-2.USB充电检测仪硬件设计
本系列文章的最终目标是制作一个USB充电检测仪,支持的功能: 显示USB充电电压、电流、功率、充电量(单位WH);实现Typec口和USB-A口的相互转换(仅支持USB 2.0); 当然网上有很多卖这种…...

如何查询服务器的端口号
要查询服务器上某个服务正在使用的端口号,可以使用几个不同的工具和方法,具体方法取决于你对服务器的访问权限以及具体的操作系统。以下是一些常用的方法: 1. 在Linux系统上 1.1 使用 netstat 命令(需要管理员权限)&…...

AU6815集成音频DSP的2x25W数字型ClaSS D音频功率放大器(替代TAS5805)
1.特性 ● 输出配置 - 立体声 2.0: 2x25W (8Ω,21V,THD N 1%) - 立体声 2.0: 2x23W (6Ω, 18V,THD N 1%) ● 供电电压范围 - PVDD:4.5V-21V - DVDD: 1.8V 或者 3.3V ● 静态功耗 - 31.5mA at PVDD12V,BD - 18.5mA at PVDD12V,1SPW ● 音频性能指标 - Noise: ≤38uVrms - TH…...

DeepSeek R1开源模型的技术突破与AI产业格局的重构
引言 2025年,中国AI企业深度求索(DeepSeek)推出的开源模型DeepSeek-R1,以低成本、高性能和开放生态为核心特征,成为全球人工智能领域的技术焦点。这一模型不仅通过算法创新显著降低算力依赖,更通过开源策…...

打破认知壁垒重构科技驱动美好生活 大模型义务传播计划
这是一份从 CUDA 到 Agentic AI 的大模型算法工程师学习路线图,旨在帮助你系统地构建成为一名优秀大模型算法工程师所需的知识体系。 阶段一:基础夯实 🧱 这个阶段的目标是掌握编程、数学和机器学习的基础知识,为后续的深度学习和…...

【Web应用】 Java + Vue 前后端开发中的Cookie、Token 和 Swagger介绍
文章目录 前言一、Cookie二、Token三、Swagger总结 前言 在现代的 web 开发中,前后端分离的架构越来越受到欢迎,Java 和 Vue 是这一架构中常用的技术栈。在这个过程中,Cookie、Token 和 Swagger 是三个非常重要的概念。本文将对这三个词进行…...

本地部署AI工作流
🧰 主流 RAG / 工作流工具对比表(含是否免费、本地部署支持与资源需求) 工具名类型是否支持 RAG可视化目标用户是否免费支持本地部署本地部署一般配置Dify企业级问答系统平台✅✅非技术 & 企业用户✅ 免费版 商业版✅ 支持2C4G 起&…...

什么是VR全景相机?如何选择VR全景相机?
VR全景相机的定义、原理及特点 定义:VR全景相机是利用特殊镜头设计和图像处理技术,能够捕捉到360度全方位、无死角的高清影像,并通过虚拟现实技术将用户带入沉浸式全景环境的相机设备。 原理:VR全景相机通过集成多个鱼眼镜头&am…...
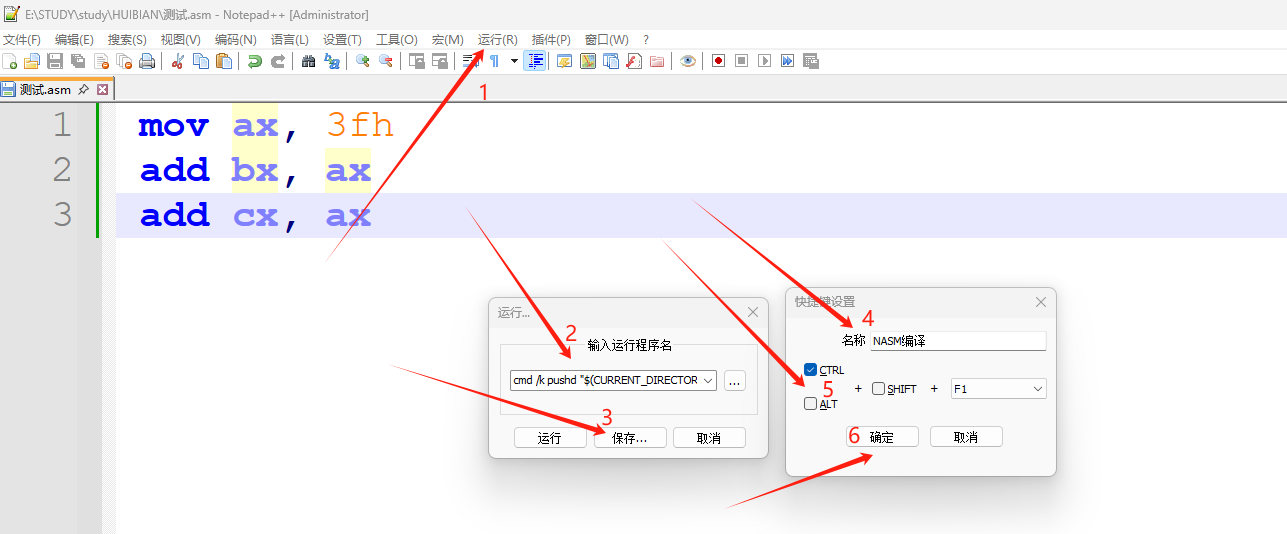
如何创建和使用汇编语言,以及下载编译汇编软件(Notepad++,NASM的安装)
一、汇编语言基础:用文本文档(Windows自带)初步尝试 1. 什么是汇编语言? 汇编语言是一种面向处理器(CPU)的低级编程语言,通过助记符(如MOV、ADD)直接控制硬件。它需要通过编译器(如…...

c++设计模式-单例模式
C++ 设计模式 - 单例模式详解 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点来获取这个实例。这种模式在软件开发中非常常见,适用于需要全局唯一实例的场景,如配置管理器、日志记录器、数据库连接池等。 单例模式的基本实现 在 C++ 中,…...

Ubuntu开机自动运行Docker容器中的Qt UI程序
Ubuntu开机自动运行Docker容器中的Qt UI程序 引言为什么需要这样配置?解决方案概览详细实现步骤1. 创建容器启动脚本2. 创建系统服务3. 配置自动登录和显示设置常见问题解决方案1. 程序无法显示(X11权限问题)2. 分辨率设置不生效3. 服务启动失败安全注意事项结语附录:完整文…...

Python训练营打卡Day40(2025.5.30)
知识点回顾: 彩色和灰度图片测试和训练的规范写法:封装在函数中展平操作:除第一个维度batchsize外全部展平dropout操作:训练阶段随机丢弃神经元,测试阶段eval模式关闭dropout # 先继续之前的代码 import torch import …...

SpringBoot+vue+SSE+Nginx实现消息实时推送
一、背景 项目中消息推送,简单的有短轮询、长轮询,还有SSE(Server-Sent Events)、以及最强大复杂的WebSocket。 至于技术选型,SSE和WebSocket区别,网上有很多,我也不整理了,大佬的链…...

python中使用高并发分布式队列库celery的那些坑
python中使用高并发分布式队列库celery的那些坑 🌟 简单理解🛠️ 核心功能🚀 工作机制📦 示例代码(使用 Redis 作为 broker)🔗 常见搭配📦 我的环境📦第一个问题…...

哈工大计算机系统大作业 程序人生-Hello’s P2P
计算机系统 大作业 题 目 程序人生-Hello’s P2P 专 业 计算机与电子通信 学 号 2023111772 班 级 23L0503 学 生 张哲瑞 指 导 教 师 …...

计算机一次取数过程分析
计算机一次取数过程分析 1 取址过程 CPU由运算器和控制器组成,其中控制器中的程序计数器(PC)保存的是下一条指令的虚拟地址,经过内存管理单元(MMU),将虚拟地址转换为物理地址,之后交给主存地址寄存器(MAR),从主存中取…...
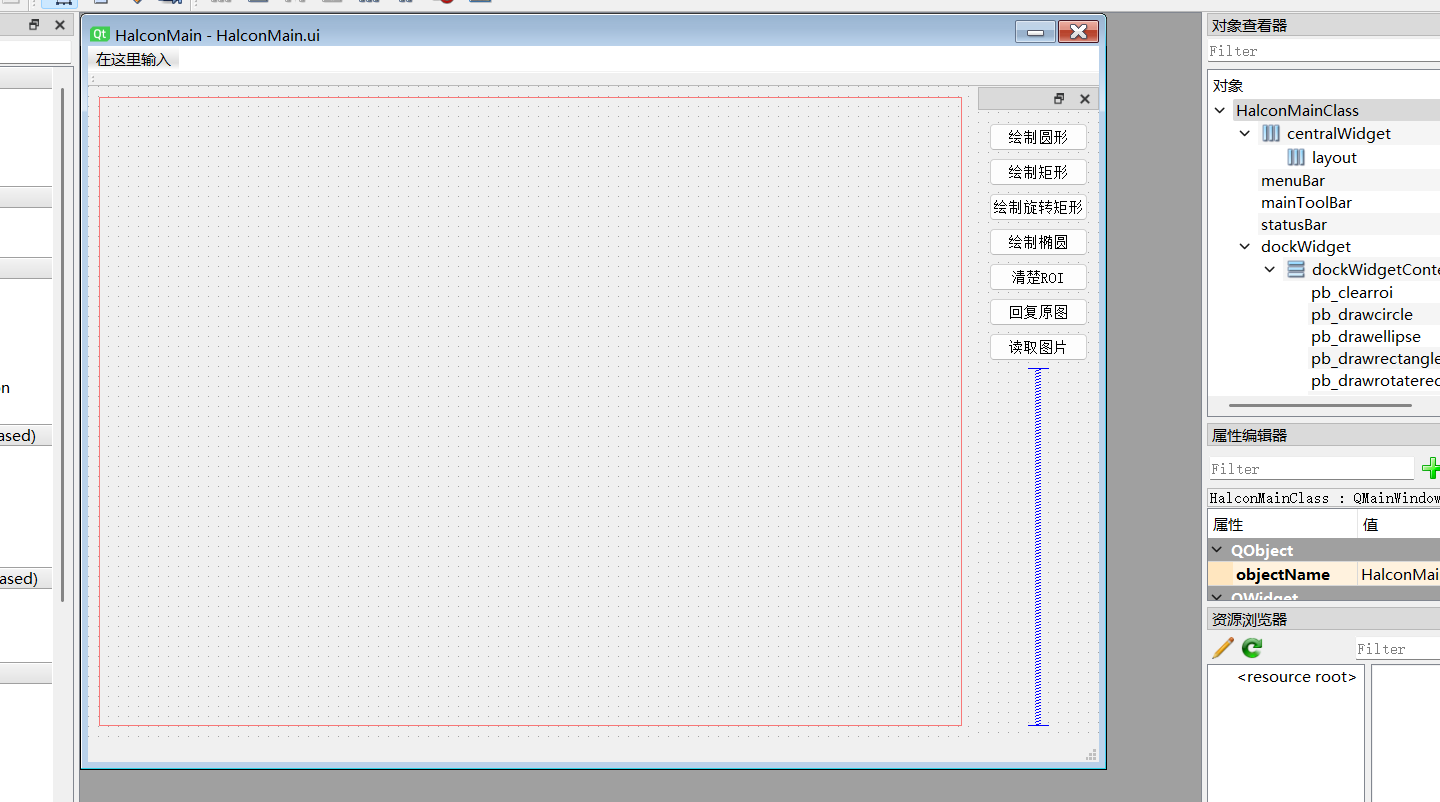
Halcon联合QT ROI绘制
文章目录 Halcon 操纵界面代码窗口代码 Halcon 操纵界面代码 #pragma once#include <QLabel>#include <halconcpp/HalconCpp.h> #include <qtimer.h> #include <qevent.h> using namespace HalconCpp;#pragma execution_character_set("utf-8&qu…...

力扣面试150题--二叉树的右视图
Day 53 题目描述 思路 采取层序遍历,利用一个high的队列来保存每个节点的高度,highb和y记录上一个节点的高度和节点,在队列中,如果队列中顶部元素的高度大于上一个节点的高度,说明上一个节点就是上一层中最右边的元素…...

数据绑定页面的完整的原理、逻辑关系、实现路径是什么?页面、表格、字段、属性、值、按钮、事件、模型、脚本、服务编排、连接器等之间的关系又是什么?
目录 一、核心概念:什么是数据绑定页面? 二、涉及的组件及其逻辑关系 页面(Page): 表格(Table): 字段(Field): 属性(Property): 值(Value): 按钮(Button): 事件(Event): 模型(Model): 脚本(Script): 服务(Service): 服务编排(Se…...

江西某石灰石矿边坡自动化监测
1. 项目简介 该矿为露天矿山,开采矿种为水泥用石灰岩,许可生产规模200万t/a,矿区面积为1.2264km2,许可开采深度为422m~250m。矿区地形为东西一北东东向带状分布,北高南低,北部为由浅变质岩系组…...

《Python 应用中的蓝绿部署与滚动更新:持续集成中的实践与优化》
《Python 应用中的蓝绿部署与滚动更新:持续集成中的实践与优化》 引言 在现代软件开发中,持续集成与持续部署(CI/CD)已成为标准实践。面对频繁发布与升级需求,蓝绿部署和滚动更新两种策略为 Python 应用提供了稳定、安全的发布方式。本文将深入探讨这两种策略的原理、适…...
