汇编语言基础: 搭建实验环境
环境配置
1.Visual Studio 创建空项目


- 创建成功

2.平台框架改为为WIN32
- 右键点击项目

- 点击属性

- 点击配置管理器

- 平台改为Win32(本文使用32位的汇编)

3.生成采用MASM
-
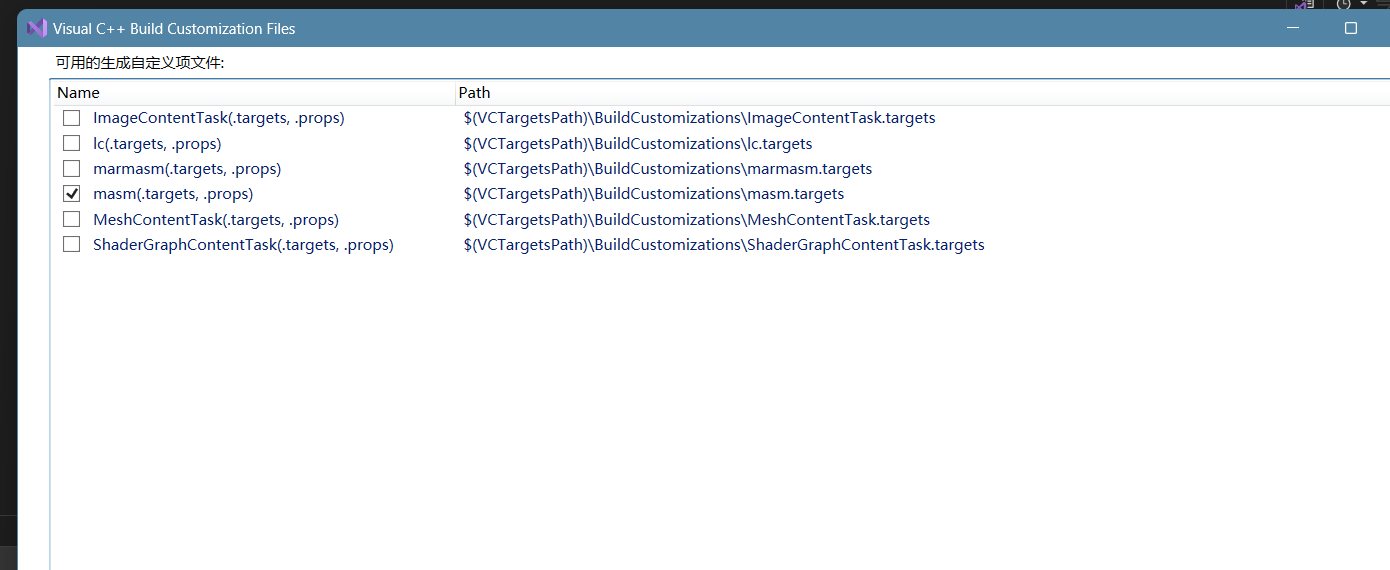
在项目属性里点击"生成依赖项"的"生成自定义"

-
勾选 masm
4.创建第一个汇编程序
- 右键源文件添加新建项,添加一个
.asm结尾的文件

- 写下如下代码
.386
.model flat,stdcall
option casemap:none
.datax dd 2
.code
_main proc
start::push ebpmov ebp,esppop ebpxor eax,eaxret
_main endp
end start
- 打一个断点编译并调试(内存中x变量值为2)

- 如果没有内存图,点击上方调试,点击窗口的内存(同样也可以调出寄存器的)

简单程序编写
- 要求:编写程序,求
sum=x+y,sum=x-y,sum=x/y,sum=x*y的结果
.386 ; 使用386指令集
.model flat, stdcall ; 平坦内存模型,stdcall调用约定
option casemap:none ; 区分大小写.datax db 8 ; 定义字节变量x,值为8y db 4 ; 定义字节变量y,值为4sum db 0 ; 定义字节变量sum,初始值为0.code
_main proc
start::push ebp ; 保存基址指针mov ebp, esp ; 设置基址指针为当前栈指针; 1. 加法运算: sum = x + ymov al, x ; 将x的值(8)加载到AL寄存器add al, y ; AL = AL + y(8+4=12)mov sum, al ; 将结果(12)存入sum; 2. 减法运算: sum = x - ymov al, x ; 重新加载x的值到ALsub al, y ; AL = AL - y(8-4=4)mov sum, al ; 将结果(4)存入sum; 3. 乘法运算: sum = x * ymov al, x ; 加载x到ALmul y ; 乘法: AL * y → AX(8*4=32)mov sum, al ; 将结果的低8位(32)存入sum; 4. 除法运算: sum = x / ymov al, x ; 加载被除数x(8)mov ah, 0 ; 清除AH寄存器(高位)mov bl, y ; 加载除数y(4)div bl ; 除法: AX / BL → 商在AL(2),余数在AHmov sum, al ; 将商(2)存入sumpop ebp ; 恢复基址指针xor eax, eax ; 将eax清零(作为程序返回值)ret ; 返回
_main endp
end start ; 指定程序入口点
代码详解
-
数据段(.data)
x db 8:定义8位字节变量x,初始值为8y db 4:定义8位字节变量y,初始值为4sum db 0:定义8位结果变量,初始化为0
-
代码段(.code)
push ebp/mov ebp, esp:标准函数开场,建立栈帧pop ebp:函数结束前恢复栈帧
-
算术运算实现
-
加法:
mov al, x ; AL = 8 add al, y ; AL = 8 + 4 = 12 mov sum, al ; sum = 12- 使用ADD指令实现加法,结果存入AL寄存器
-
减法:
mov al, x ; 重新加载x值(因AL已被修改) sub al, y ; AL = 8 - 4 = 4 mov sum, al ; sum = 4- SUB指令实现减法,需注意寄存器值的覆盖问题
-
乘法:
mov al, x ; AL = 8 mul y ; AX = AL * y = 8 * 4 = 32 mov sum, al ; sum = AL = 32- MUL指令执行无符号乘法
- 结果存储在AX(16位)中,AL包含低8位
-
除法:
mov al, x ; AL = 8(被除数低8位) mov ah, 0 ; AH = 0(被除数高8位) mov bl, y ; BL = 4(除数) div bl ; AL = AX/BL = 8/4 = 2(商) mov sum, al ; sum = 2- DIV指令执行无符号除法
- 被除数必须在AX中(16位)
- 商存储在AL,余数在AH
-
-
程序退出
xor eax, eax:将EAX清零,作为程序返回值ret:从过程返回
调试技巧
- 在关键指令后设置断点(F9)
- 使用内存窗口(调试→窗口→内存)查看变量值
- 使用寄存器窗口(调试→窗口→寄存器)观察寄存器变化
- 单步执行(F10/F11)跟踪指令执行流程
注意事项
- 乘法结果可能超出8位(如本例中8*4=32仍在8位范围内)
- 除法前必须清除AH寄存器(16位除法)
- 连续运算时需注意寄存器值的覆盖问题
- Win32汇编使用平坦内存模型(flat),无分段概念
- 确保使用正确的调用约定(stdcall)
相关文章:

汇编语言基础: 搭建实验环境
环境配置 1.Visual Studio 创建空项目 创建成功 2.平台框架改为为WIN32 右键点击项目 点击属性 点击配置管理器 平台改为Win32(本文使用32位的汇编) 3.生成采用MASM 在项目属性里点击"生成依赖项"的"生成自定义" 勾选 masm 4.创建第一个汇编程序 右…...

SIFT 算法原理详解
SIFT 算法原理详解 SIFT(尺度不变特征变换,Scale-Invariant Feature Transform)是一种经典的局部特征检测和描述算法,它能够在不同的尺度、旋转和光照变化下稳定地检测图像特征。SIFT 主要包括以下几个步骤:尺度空间极…...

基于springboot的益智游戏系统的设计与实现
博主介绍:java高级开发,从事互联网行业六年,熟悉各种主流语言,精通java、python、php、爬虫、web开发,已经做了六年的毕业设计程序开发,开发过上千套毕业设计程序,没有什么华丽的语言࿰…...

短剧系统开发文案:打造沉浸式互动娱乐新体验
一、项目背景 随着短视频与碎片化娱乐的兴起,短剧市场呈现爆发式增长。用户对剧情紧凑、节奏明快、互动性强的内容需求激增,传统影视平台已难以满足个性化与参与感需求。「XX短剧系统」应运而生,致力于打造集内容创作、分发、互动于一体的短…...

第十二节:第四部分:集合框架:List系列集合:LinkedList集合的底层原理、特有方法、栈、队列
LinkedList集合的底层原理 LinkedList集合的应用场景之一 代码:掌握LinkedList集合的使用 package com.itheima.day19_Collection_List;import java.util.LinkedList; import java.util.List;//掌握LinkedList集合的使用。 public class ListTest3 {public static …...

多模态大语言模型arxiv论文略读(104)
Talk Less, Interact Better: Evaluating In-context Conversational Adaptation in Multimodal LLMs ➡️ 论文标题:Talk Less, Interact Better: Evaluating In-context Conversational Adaptation in Multimodal LLMs ➡️ 论文作者:Yilun Hua, Yoav…...

【C++高级主题】多重继承下的类作用域
目录 一、类作用域与名字查找规则:理解二义性的根源 1.1 类作用域的基本概念 1.2 单继承的名字查找流程 1.3 多重继承的名字查找特殊性 1.4 关键规则:“最近” 作用域优先,但多重继承无 “最近” 二、多重继承二义性的典型类型与代码示…...

基于Android的一周穿搭APP的设计与实现 _springboot+vue
开发语言:Java框架:springboot AndroidJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7数据库工具:Navicat12开发软件:eclipse/myeclipse/ideaMaven包:Maven3.6 系统展示 APP登录 A…...

机器学习——使用多个决策树
使用单一决策树的弱点之一是决策树对数据中的微小变化非常敏感,一个使算法不那么敏感或更健壮的解决方案,不是建立一个决策树,而是要建立大量的决策树,我们称之为树合奏。 在这个例子中,我们一直在使用最好的特性来分…...

C# 中的对话框与导航:构建流畅用户交互的完整指南
在现代应用程序开发中,良好的用户交互体验是成功的关键因素之一。作为.NET开发者,熟练掌握C#中的对话框与导航技术,能够显著提升应用程序的易用性和专业性。本文将全面探讨Windows Forms、WPF、ASP.NET Core和MAUI等平台下的对话框与导航实现…...

DeepSeek - 尝试一下GitHub Models中的DeepSeek
1.简单介绍 当前DeepSeek使用的人很多,各大AI平台中也快速引入了DeekSeek,比如Azure AI Foundary(以前名字是Azure AI Studio)中的Model Catalog, HuggingFace, GitHub Models等。同时也出现了一些支持DeepSeek的.NET类库。微软的Semantic Kernel也支持…...

【判断酒酒花数】2022-3-31
缘由对超长正整数的处理? - C语言论坛 - 编程论坛 void 判断酒酒花数(_int64 n) {//缘由https://bbs.bccn.net/thread-508634-1-1.html_int64 t n; int h 0, j 0;//while (j < 3)h t % 10, t / 10, j;//整数的个位十位百位之和是其前缀while (t > 0)h t…...

对称加密-非对称加密
目录 非对称加密算法的优缺点是什么? 一、非对称加密的核心特点 二、非对称加密的显著优点 1. 解决密钥分发难题 2. 支持数字签名 3. 前向安全性 4. 访问控制灵活性 三、非对称加密的局限性 1. 性能瓶颈 2. 密钥长度要…...
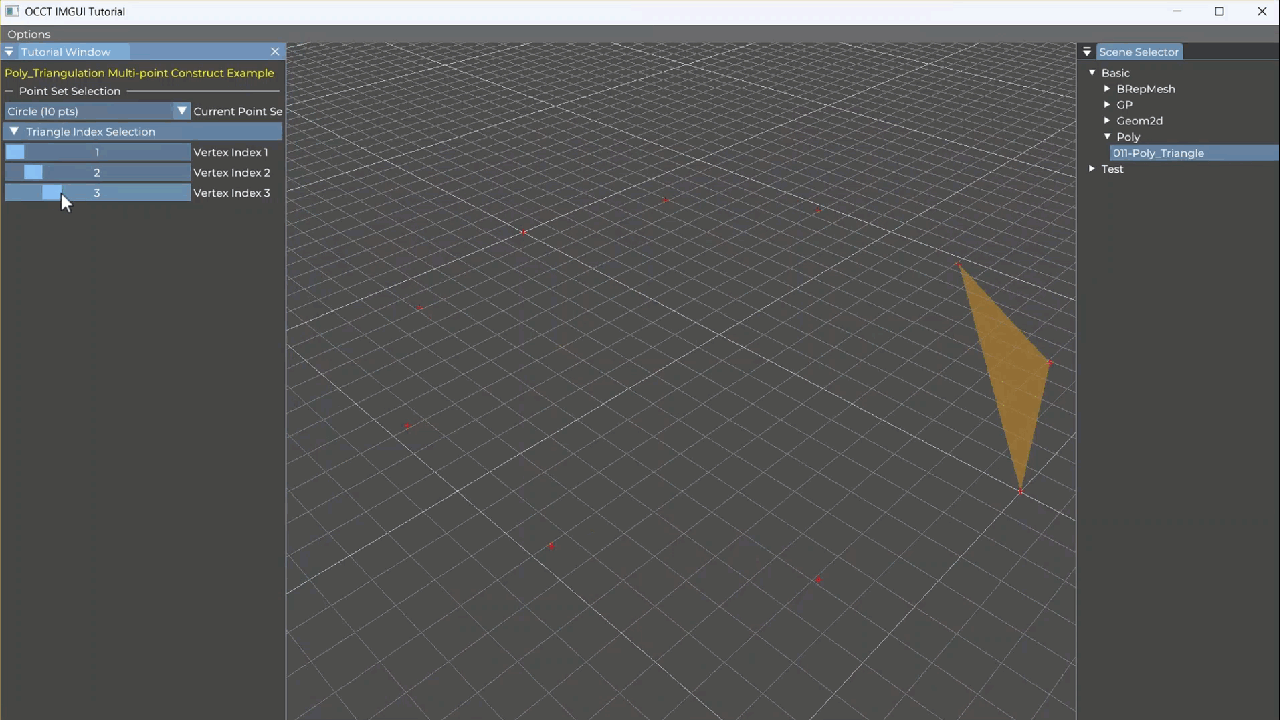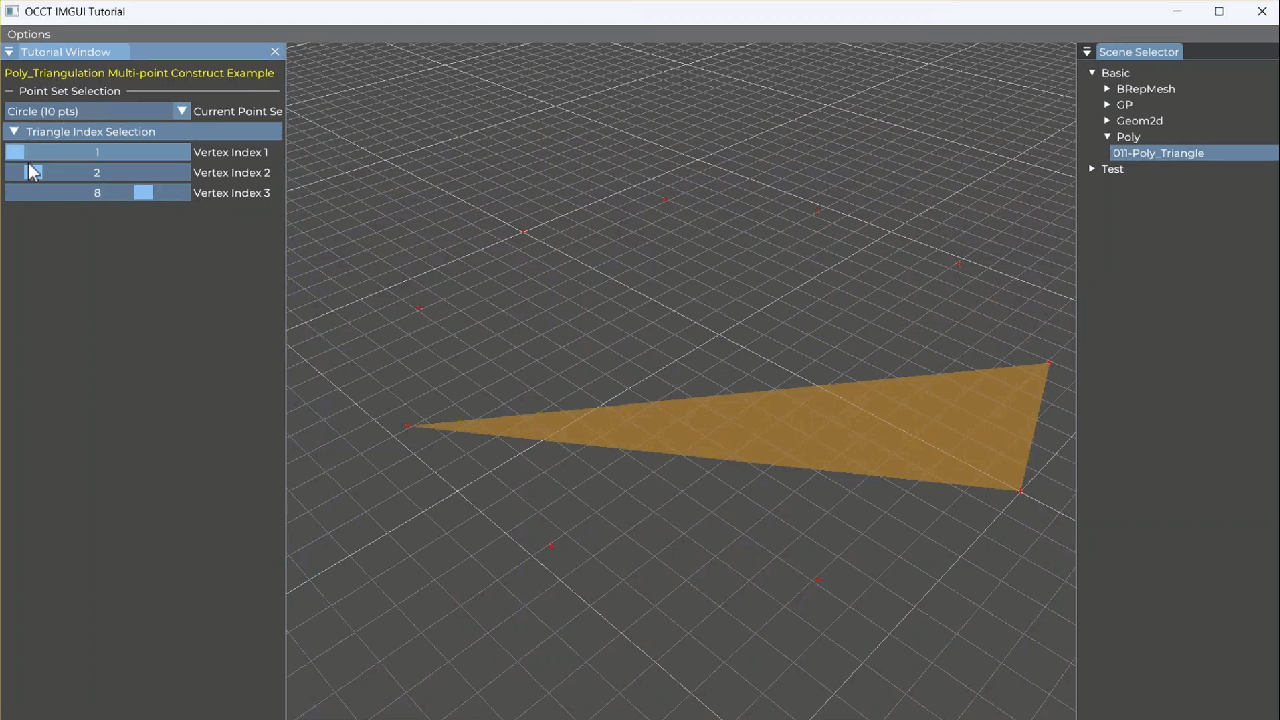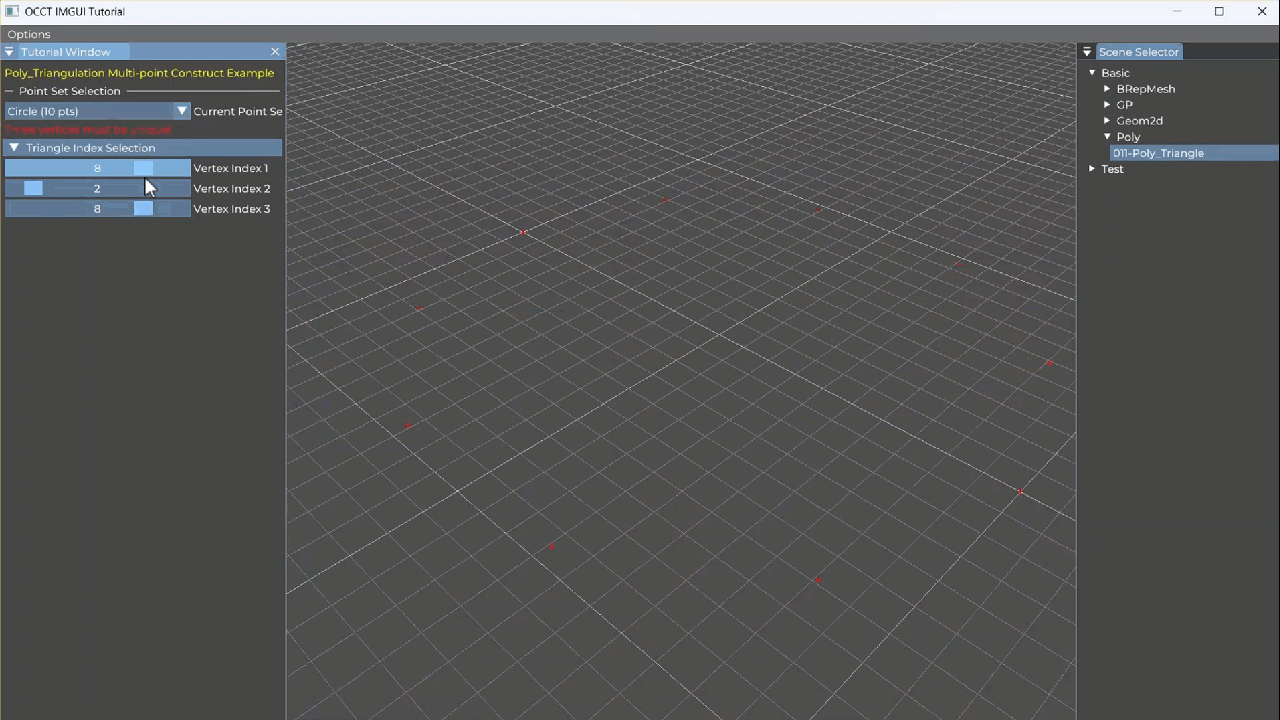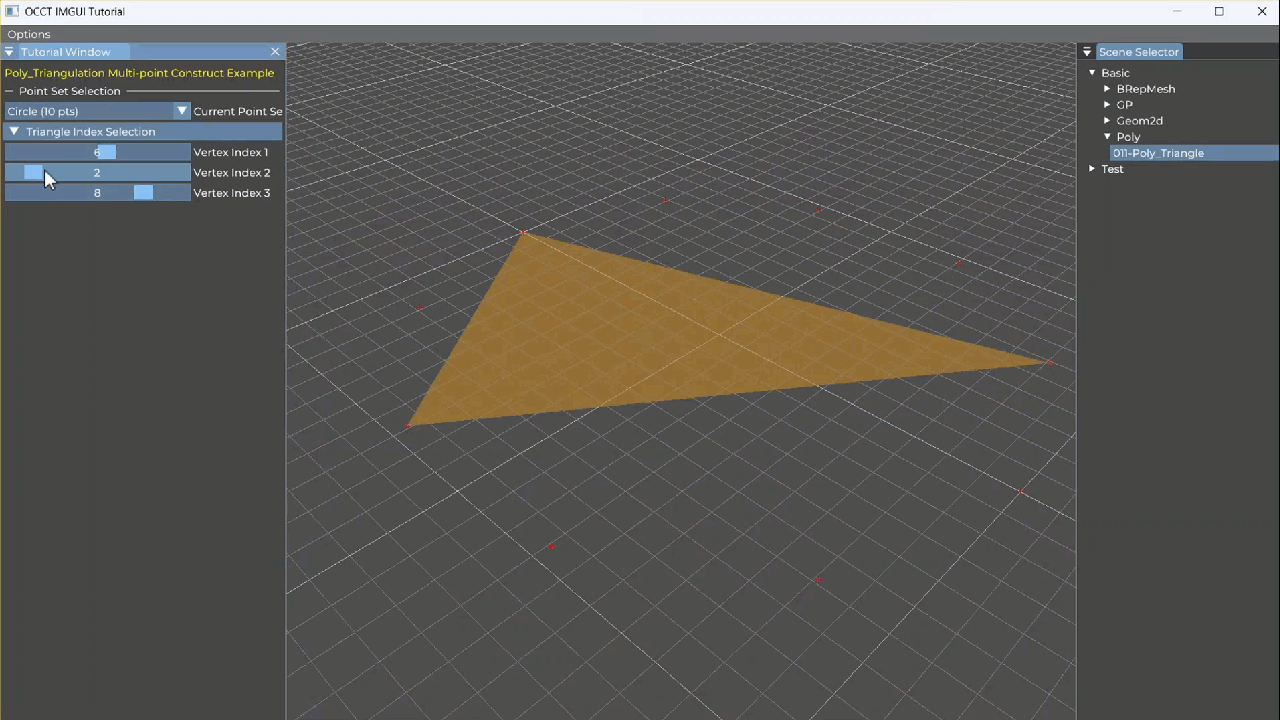
【OCCT+ImGUI系列】011-Poly-Poly_Triangle三角形面片
Poly_Triangle 是什么? Poly_Triangle 是一个非常轻量的类,用于表示一个三角网格中的单个三角形面片。它是构成 Poly_Triangulation(三角网格对象)的基本单位之一。之后会写关于碰撞检测的相关文章,三角面片是非常重要…...

【机器学习基础】机器学习入门核心算法:Mini-Batch K-Means算法
机器学习入门核心算法:Mini-Batch K-Means算法 一、算法逻辑工作流程与传统K-Means对比 二、算法原理与数学推导1. 目标函数2. Mini-Batch更新规则3. 学习率衰减机制4. 伪代码 三、模型评估1. 内部评估指标2. 收敛性判断3. 超参数调优 四、应用案例1. 图像处理 - 颜…...

机器学习实战36-基于遗传算法的水泵调度优化项目研究与代码实现
大家好,我是微学AI,今天给大家介绍一下机器学习实战36-基于遗传算法的水泵调度优化项目研究与代码实现。 文章目录 一、项目介绍二、项目背景三、数学原理与算法分析动态规划模型遗传算法设计编码方案适应度函数约束处理算法参数能量消耗模型一泵房能耗二泵房能耗效率计算模…...

计算机视觉与深度学习 | 基于Matlab的门禁指纹识别与人脸识别双系统实现
系统架构 #mermaid-svg-d8CEMhB3dNDpJu8M {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-d8CEMhB3dNDpJu8M .error-icon{fill:#552222;}#mermaid-svg-d8CEMhB3dNDpJu8M .error-text{fill:#552222;stroke:#552222;}#…...

TypeScript 定义同步方法
在TypeScript中定义同步方法是一个常见的需求,尤其是在处理不涉及异步操作的情况下。本文将详细介绍如何在TypeScript中定义和使用同步方法,包括代码示例和详细解释。 一、定义同步方法 在TypeScript中,定义同步方法与JavaScript类似&#…...

debian12.9或ubuntu,vagrant离线安装插件vagrant-libvirt,20250601
系统盘: https://mirror.lzu.edu.cn/debian-cd/12.9.0/amd64/iso-dvd/debian-12.9.0-amd64-DVD-1.iso 需要的依赖包,无需安装ruby( sudo apt install -y ruby-full ruby-dev rubygems,后来发现不安装会有编译警告,还是安装吧 ) ,无需安装 zlib1g-dev liblzma-dev libxml2-de…...

【仿muduo库实现并发服务器】使用正则表达式提取HTTP元素
使用正则表达式提取HTTP元素 1.正则表达式2.正则库的使用3.使用正则表达式提取HTTP请求行 1.正则表达式 正则表达式它其实是描述了一种字符串匹配的模式,它可以用来在一个字符串中检测一个特定格式的字串,以及可以将符合特定规则的字串进行替换或者提取…...

核心机制:流量控制
搭配滑动窗口使用的 窗口大小 窗口越大,传输速度就越快,但是也不能无限大,太大了,对于可靠性会有影响 比如发生方以非常快的速度,发送,接收方的处理速度跟不上,也就会导致有效数据被接受方丢弃(又得重传) 流量控制,就是根据接收方的处理能力(如何衡量?),干预到发送方的发送…...

Java中并发修改异常如何处理
在 Java 中,ConcurrentModificationException(并发修改异常) 是遍历集合时最常见的错误之一。它发生在迭代过程中直接修改集合结构(添加/删除元素)时,与是否多线程无关。以下是详细的处理方案: …...

极智项目 | 基于PyQT实现的YOLOv12行人目标检测软件设计
基于YOLOv12的专业级行人目标检测软件应用 开发者: 极智视界 软件下载:链接 🌟 项目特色 专业检测: 基于最新YOLOv12模型,专门针对行人检测优化现代界面: 采用PyQt5构建的美观、直观的图形用户界面高性能: 支持GPU加速,检测速…...

JavaScript 对象展开语法
文章目录 JavaScript 对象展开语法1、对象展开(Spread)操作:2、组件注册3、示例应用总结 JavaScript 对象展开语法 示例代码: export default {...student,components: {ConponentA: ConponentA,ConponentB: ConponentB},这段代…...

简单transformer运用
通俗易懂解读:hw04.py 文件内容与 Transformer 的应用 这个文件是一个 Python 脚本(hw04.py),用于完成 NTU 2021 Spring 机器学习课程的 HW4 作业任务:扬声器分类(Speaker Classification)。它…...

vscode不满足先决条件问题的解决——vscode的老版本安装与禁止更新(附安装包)
目录 起因 vscode更新设置的关闭 安装包 结语 起因 由于主包用的系统是centos的,且版本有点老了,再加上vscode现在不支持老版本的,这对主包来说更是雪上加霜啊 但是主包看了网上很多教程,眼花缭乱,好多配置要改&…...

RustDesk 搭建自建服务器并设置服务自启动
目录 0. 介绍 1. 事前准备 1.1 有公网 ip 的云服务器一台 1.2 服务端部署包 1.3 客户端安装包 2. 部署 2.1 服务器环境准备 2.2 上传服务端部署包 2.3 运行 pm2 3. 客户端使用 3.1 安装 3.2 配置 3.2.1 解锁网络设置 3.2.2 ID / 中级服务器 3.3 启动效果 > …...

【数据库】数据库恢复技术
数据库恢复技术 实现恢复的核心是使用冗余,也就是根据冗余数据重建不正确数据。 事务 事务是一个数据库操作序列,是一个不可分割的工作单位,是恢复和并发的基本单位。 在关系数据库中,一个事务是一条或多条SQL语句,…...

Qt企业级串口通信实战:高效稳定的工业级应用开发指南
目录 一、前言 二、问题代码剖析 2.1 典型缺陷示例 2.2 企业级应用必备特性对比 三、关键优化策略与代码实现 3.1 增强型串口管理类 问题1:explicit关键字的作用 3.2 智能错误恢复机制 3.3 数据分帧处理算法 四、性能优化实测数据 五、工业级应用场景 六…...

力扣HOT100之动态规划:32. 最长有效括号
这道题放在动态规划里属实是有点难为人了,感觉用动态规划来做反而更难理解了,这道题用索引栈来做相当好理解,这里先讲下索引栈的思路。 索引栈做法 我们定义一个存放整数的栈,定义一个全局变量result来记录最长有效子串的长度&a…...
