24考研数据结构-数组和特殊矩阵
目录
- 数据结构:数组与特殊矩阵
- 数组
- 数组的特点
- 数组的用途
- 特殊矩阵
- 对角矩阵
- 上三角矩阵和下三角矩阵
- 稀疏矩阵
- 特殊矩阵的用途
- 结论
- 3.4 数组和特殊矩阵
- 3.4.1数组的存储结构
- 3.4.2普通矩阵的存储
- 3.4.3特殊矩阵的存储
- 1. 对称矩阵(方阵)
- 2. 三角矩阵(方阵)
- 3. 三对角矩阵(方阵)带状
- 4. 稀疏矩阵
数据结构:数组与特殊矩阵
数据结构是计算机科学中的基础概念,它涉及组织和存储数据的方式以及对数据的操作。在数据结构中,数组和特殊矩阵是两种常见的数据组织形式。本文将对数组和特殊矩阵进行介绍,并讨论它们在实际应用中的特点和用途。
数组
数组是一种线性数据结构,它由相同类型的元素按照一定顺序组成。数组的特点是在内存中连续存储元素,可以通过索引快速访问其中的元素。数组的索引通常从0开始,表示数组中元素的位置。例如,一个长度为n的数组A,其元素可以表示为A[0]、A[1]、A[2]、…、A[n-1]。
数组的特点
- 快速访问:由于数组中元素在内存中连续存储,可以通过索引直接访问数组中的元素,具有快速访问的特点。
- 固定大小:数组在创建时需要指定大小,且大小固定,无法在运行时动态改变大小。
- 存储效率高:由于元素在内存中连续存储,使得数组的存储效率较高。
数组的用途
数组在实际应用中有着广泛的用途,例如:
- 数据存储:用于存储一系列数据元素,如整数、字符、浮点数等。
- 数据统计:用于统计一组数据中的最大值、最小值、平均值等。
- 排序算法:在各种排序算法中,数组是常用的数据结构。
数组的使用非常灵活,它在算法和数据处理领域有着重要的地位。
特殊矩阵
特殊矩阵是一种二维数据结构,它具有某种特殊的规律或特点,使得在特定情况下能够对其进行更高效的存储和操作。特殊矩阵通常有以下几种类型:
对角矩阵
对角矩阵是一种除了主对角线以外的所有元素都为零的矩阵。例如,一个n阶对角矩阵D可以表示为:
d[i][j] = 0, i ≠ j
d[i][j] ≠ 0, i = j
对角矩阵在存储和运算时,可以只保存主对角线上的元素,大大节省了存储空间和运算时间。
上三角矩阵和下三角矩阵
上三角矩阵和下三角矩阵是一种在主对角线上方或下方的所有元素都为零的矩阵。上三角矩阵的下方元素都为零,下三角矩阵的上方元素都为零。这些矩阵在存储和运算时,也可以只保存非零元素,节省存储空间和运算时间。
稀疏矩阵
稀疏矩阵是一种大部分元素都为零的矩阵。在实际应用中,很多矩阵都是稀疏矩阵,例如图像处理中的像素矩阵。对于稀疏矩阵,存储所有元素将会浪费大量的存储空间。因此,可以采用压缩存储方法,只存储非零元素及其位置,从而节省存储空间。
特殊矩阵的用途
特殊矩阵在很多领域都有着广泛的应用,尤其在数值计算和科学工程中。它们可以优化矩阵的存储和运算效率,提高算法的执行速度。
结论
数组和特殊矩阵是两种常见的数据结构,在计算机科学和工程中都有着广泛的应用。数组是一种简单而高效的数据组织形式,用于存储一系列相同类型的元素。特殊矩阵是一种具有特殊规律的二维数据结构,能够优化矩阵的存储和运算效率。
在实际应用中,我们可以根据具体问题的特点选择合适的数据结构,以提高算法的效率和性能。同时,对于特殊矩阵,我们可以采用压缩存储方法来节省存储空间,使得数据处理更加高效和便捷。通过合理选择和使用数据结构,我们可以优化算法的执行效率,提高计算机程序的性能。
3.4 数组和特殊矩阵
矩阵定义: 一个由m*n个元素排成的m行(横向)n列(纵向)的表。
矩阵的常规存储:将矩阵描述为一个二维数组。
3.4.1数组的存储结构
- 一维数组
Elemtype a[10];
各数组元素大小相同,物理上连续存放;
起始地址:LOC
数组下标:默认从0开始!
数组元素 a[i] 的存放地址 = LOC + i × sizeof(ElemType)

- 二维数组
Elemtype b[2][4]; //2行4列的二维数组
行优先/列优先存储优点:实现随机存储

起始地址:LOC
M行N列的二维数组 b[M][N] 中,b[i][j]的存储地址:
行优先存储: LOC + (i×N + j) × sizeof(ElemType)
列优先存储:LOC + (j×M + i) × sizeof(ElemType)
3.4.2普通矩阵的存储
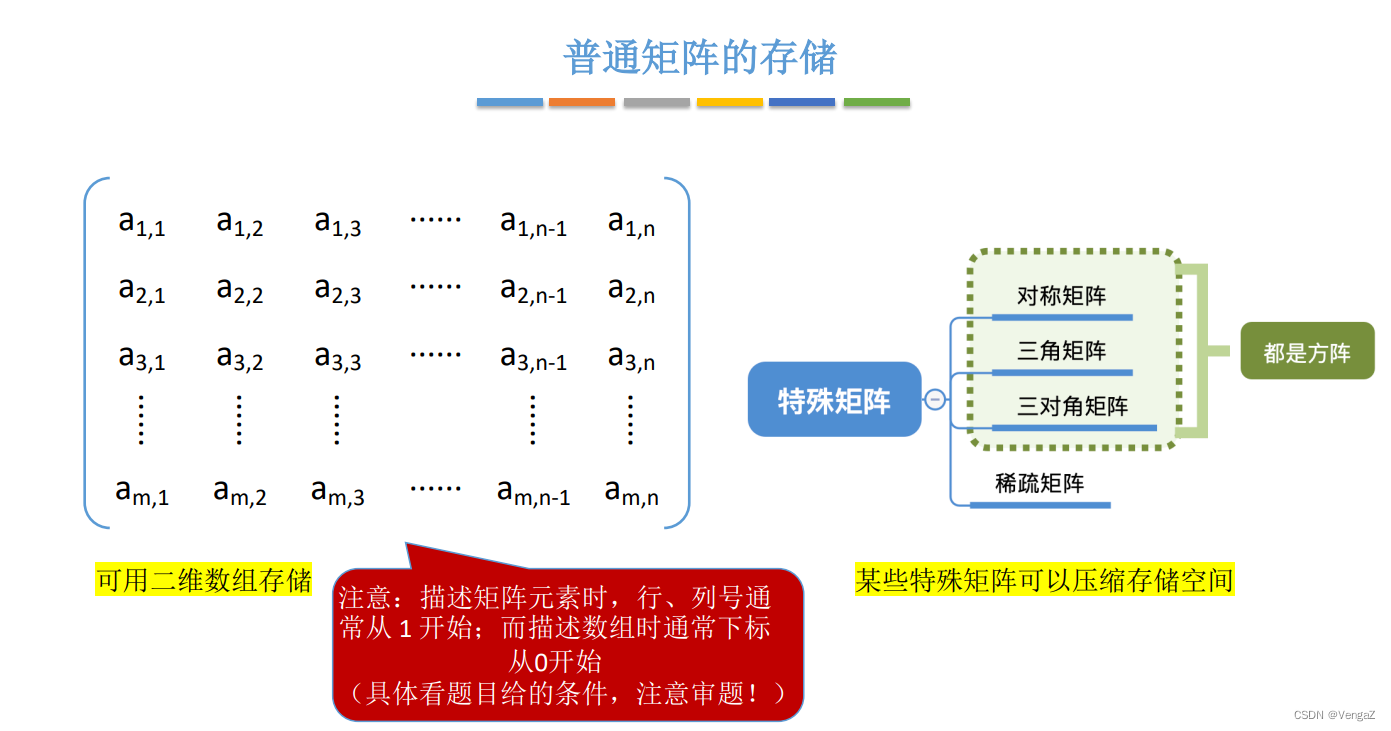
二维数组存储:
- 描述矩阵元素时,行、列号通常从1开始;
- 描述数组时,通常下标从 0 开始;
3.4.3特殊矩阵的存储
特殊矩阵——压缩存储空间(只存有用的数据)
矩阵的压缩存储:为多个相同的非零元素只分配一个存储空间;对零元素不分配空间。
1. 对称矩阵(方阵)
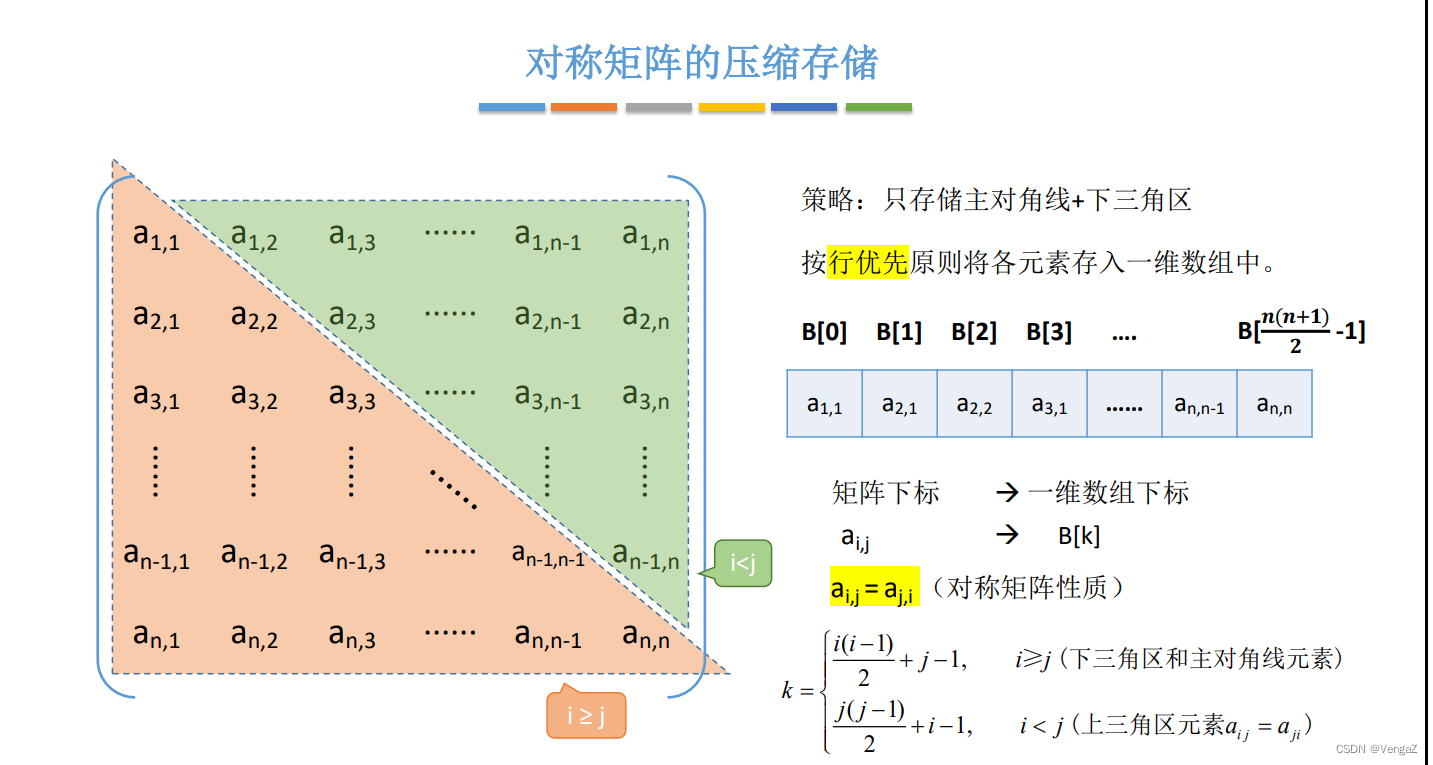
列优先:
-
n >1
n+ (n-1)+ ······+(i-j)+1 -
n = 1
i-j+1
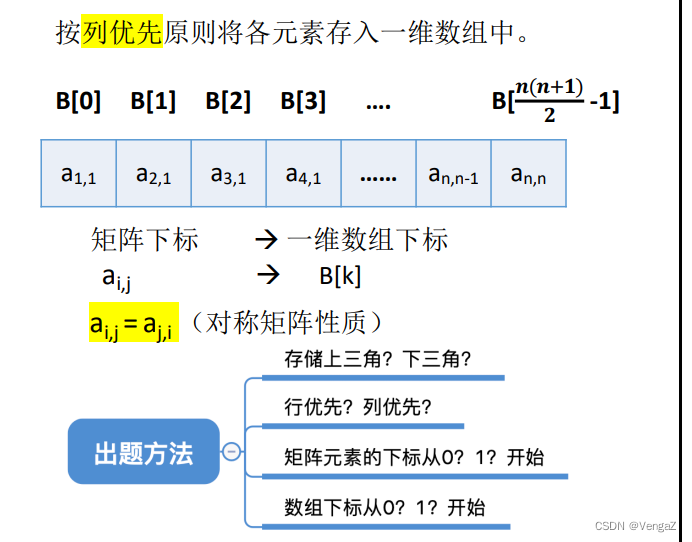
2. 三角矩阵(方阵)
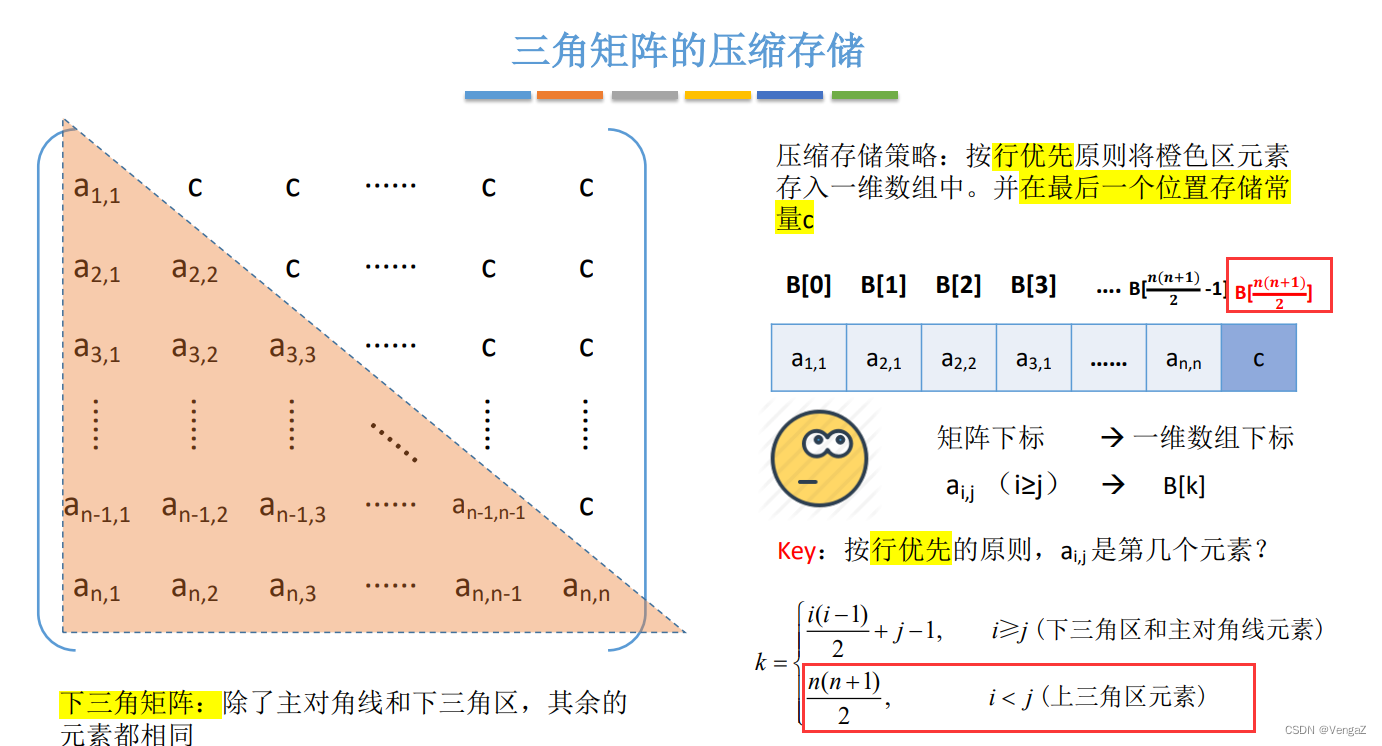
n + (n-1) +······(n-i+1) +(j-i)
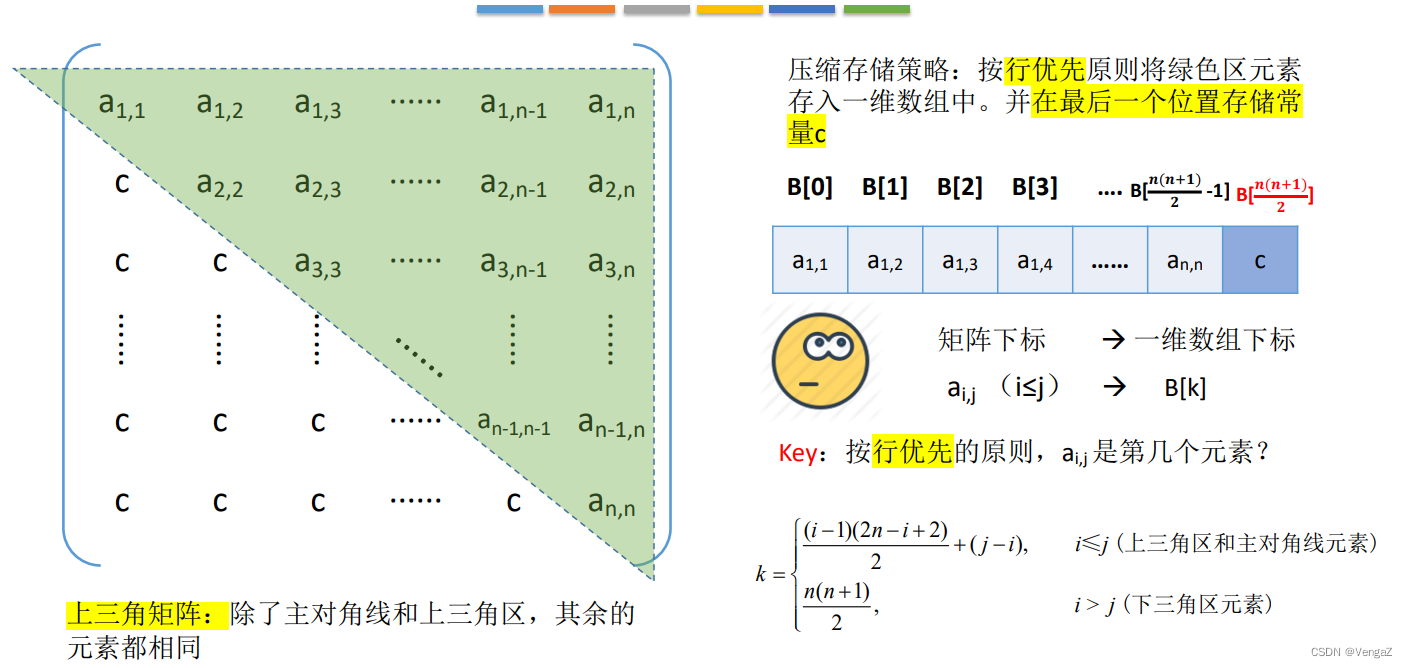
3. 三对角矩阵(方阵)带状
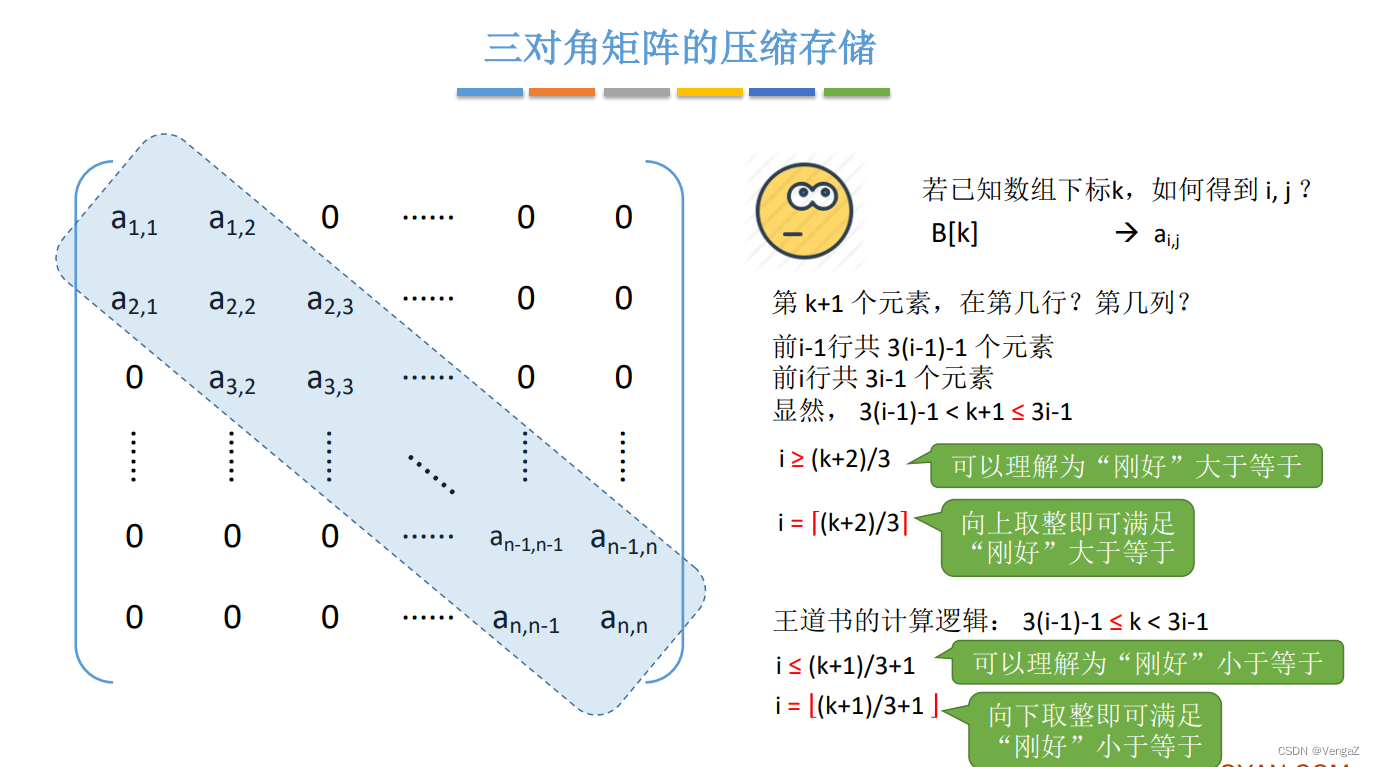

4. 稀疏矩阵
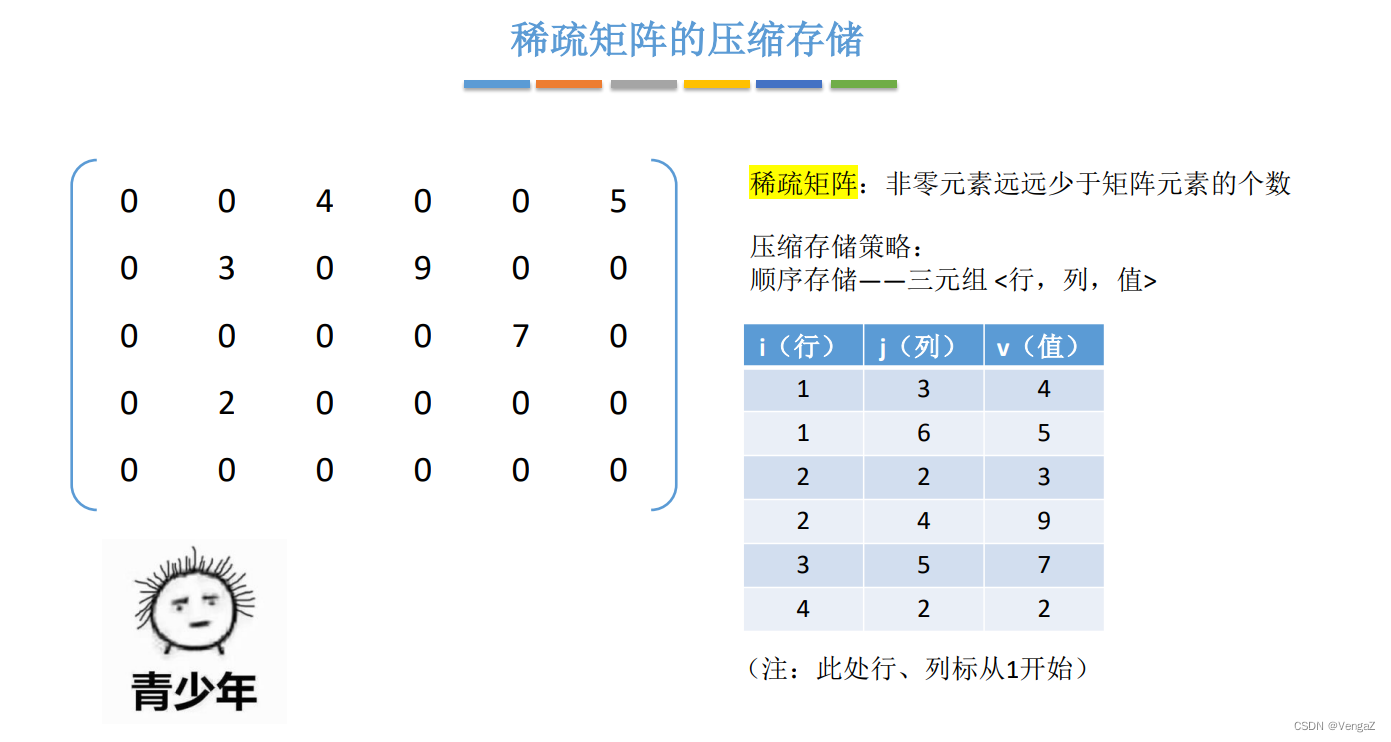
设在mn的矩阵中有t个非零元素,令c=t/(mn),当c<=0.05时称为稀疏矩阵。
压缩存储原则:存各非零元的值、行列位置和矩阵的行列数。
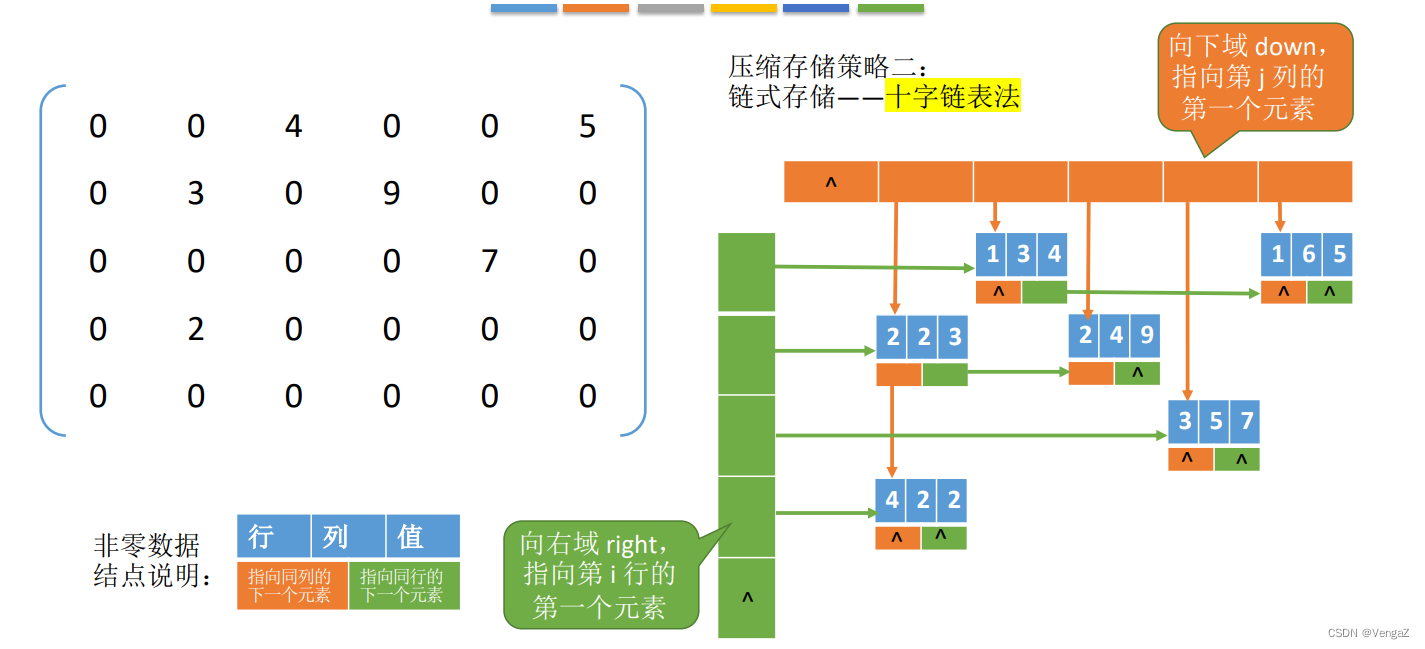
相关文章:

24考研数据结构-数组和特殊矩阵
目录 数据结构:数组与特殊矩阵数组数组的特点数组的用途 特殊矩阵对角矩阵上三角矩阵和下三角矩阵稀疏矩阵特殊矩阵的用途 结论 3.4 数组和特殊矩阵3.4.1数组的存储结构3.4.2普通矩阵的存储3.4.3特殊矩阵的存储1. 对称矩阵(方阵)2. 三角矩阵(方阵)3. 三对角矩阵(方阵…...

服务器后台运行程序
代码运行 要让代码在服务器后台运行,有多种方法。在 Linux 系统中,最常见的有以下几种方式: **1. 使用 & 符号:** 在命令后面添加 & 符号可以让程序在后台运行。例如: bash python myscript.py &但是…...
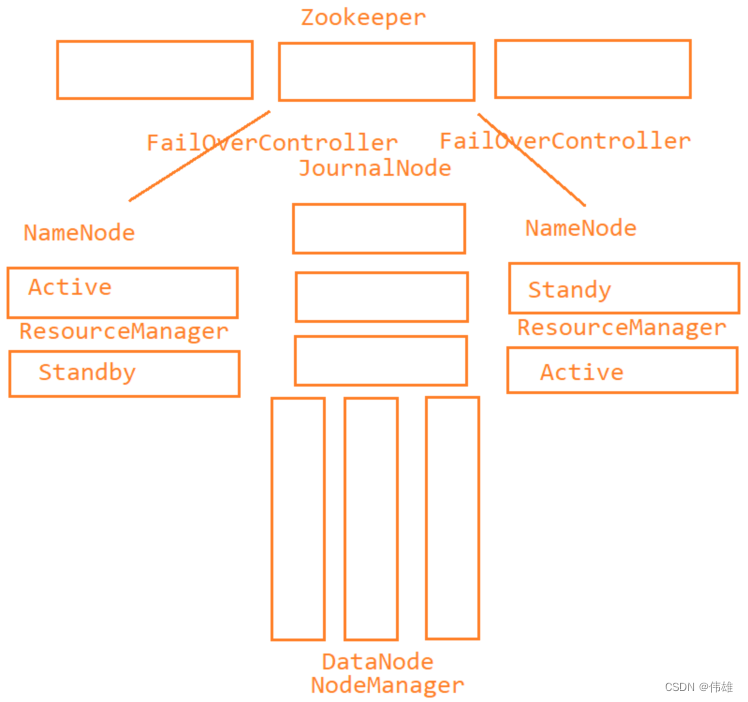
大数据课程D7——hadoop的YARN
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解YARN的概念和结构; ⚪ 掌握YARN的资源调度流程; ⚪ 了解Hadoop支持的资源调度器:FIFO、Capacity、Fair; ⚪ 掌握YA…...

Rust vs Go:常用语法对比(十三)
题图来自 Go vs. Rust: The Ultimate Performance Battle 241. Yield priority to other threads Explicitly decrease the priority of the current process, so that other execution threads have a better chance to execute now. Then resume normal execution and call f…...

【【51单片机DA转换模块】】
爆改直流电机,DA转换器 main.c #include <REGX52.H> #include "Delay.h" #include "Timer0.h"sbit DAP2^1;unsigned char Counter,Compare; //计数值和比较值,用于输出PWM unsigned char i;void main() {Timer0_Init();whil…...

[SQL挖掘机] - 字符串函数 - substring
介绍: substring函数是在mysql中用于提取字符串的一种函数。它接受一个字符串作为输入,并返回从该字符串中指定位置开始的一部分子串。substring函数可以用于获取字符串中的特定字符或子串,以便进行进一步的处理或分析。 用法: 下面是substring函数的…...
第一百一十六天学习记录:C++提高:STL-string(黑马教学视频)
string基本概念 string是C风格的字符串,而string本质上是一个类 string和char区别 1、char是一个指针 2、string是一个类,类内部封装了char*,管理这个字符串,是一个char型的容器。 特点: string类内部封装了很多成员方…...
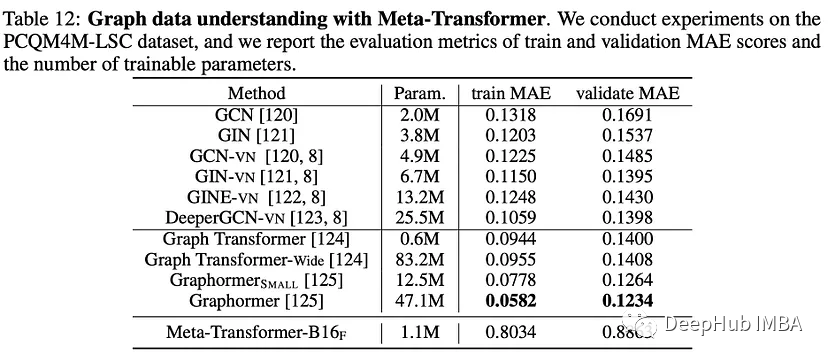
Meta-Transformer 多模态学习的统一框架
Meta-Transformer是一个用于多模态学习的新框架,用来处理和关联来自多种模态的信息,如自然语言、图像、点云、音频、视频、时间序列和表格数据,虽然各种数据之间存在固有的差距,但是Meta-Transformer利用冻结编码器从共享标记空间…...
tinkerCAD案例:24.Tinkercad 中的自定义字体
tinkerCAD案例:24.Tinkercad 中的自定义字体 原文 Tinkercad Projects Tinkercad has a fun shape in the Shape Generators section that allows you to upload your own font in SVG format and use it in your designs. I’ve used it for a variety of desi…...
list与流迭代器stream_iterator
运行代码: //list与流迭代器 #include"std_lib_facilities.h" //声明Item类 struct Item {string name;int iid;double value;Item():name(" "),iid(0),value(0.0){}Item(string ss,int ii,double vv):name(ss),iid(ii),value(vv){}friend ist…...

九耶:冯·诺伊曼体系
冯诺伊曼体系(Von Neumann architecture)是一种计算机体系结构,它由匈牙利数学家冯诺伊曼于1945年提出。冯诺伊曼体系是现代计算机体系结构的基础,几乎所有的通用计算机都采用了这种体系结构。 冯诺伊曼体系的核心思想是将计算机硬…...
探索UCI心脏病数据:利用R语言和h2o深度学习构建预测模型
一、引言 随着机器学习模型在实际应用中的广泛应用,人们对于模型的解释性和可理解性日益关注。可解释性机器学习是指能够清晰、透明地解释机器学习模型决策过程的一种方法和技术。在许多领域中,如医疗诊断、金融风险评估和自动驾驶等,解释模型…...
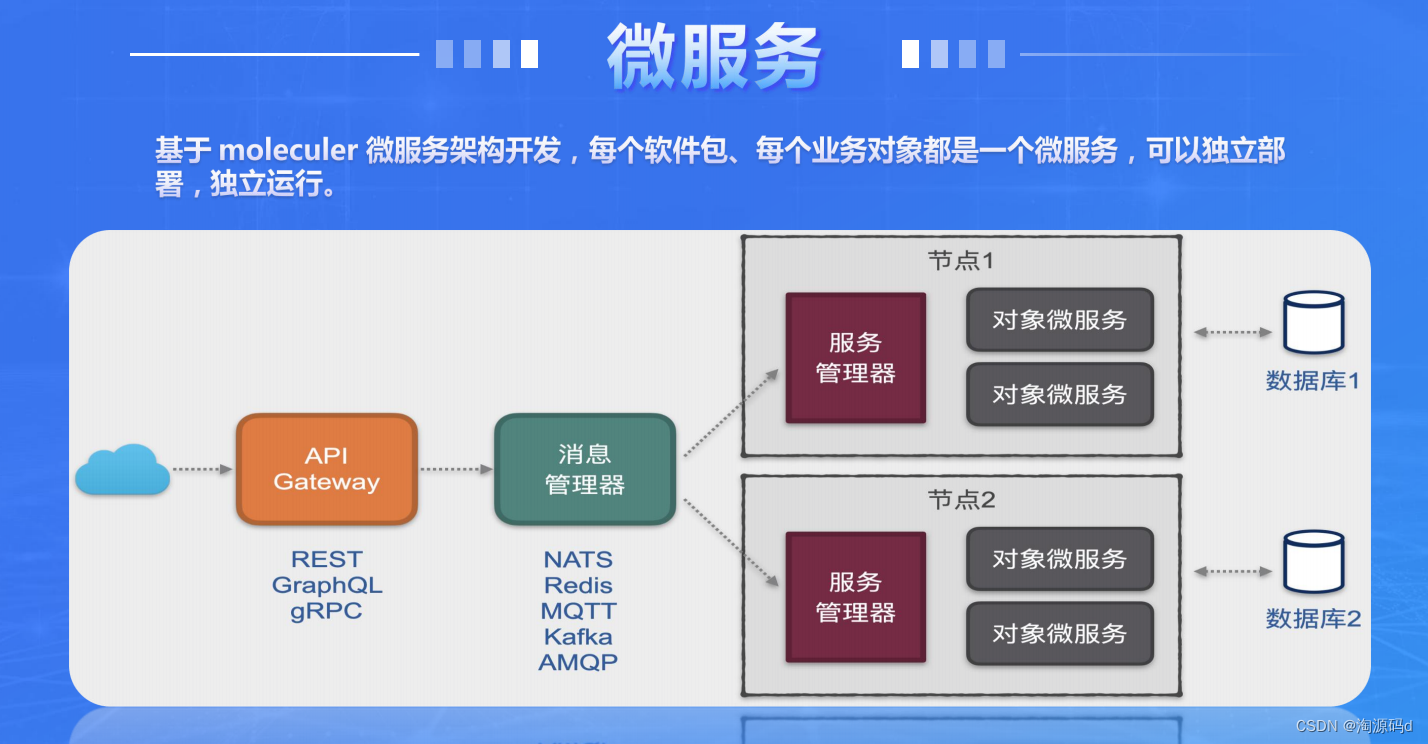
基于 moleculer 微服务架构的智能低代码PaaS 平台源码 可视化开发
低代码开发平台源码 低代码管理系统PaaS 平台 无需代码或通过少量代码就可以快速生成应用程序的开发平台。 本套低代码管理后台可以支持多种企业应用场景,包括但不限于CRM、ERP、OA、BI、IoT、大数据等。无论是传统企业还是新兴企业,都可以使用管理后台…...

xrdp登录显示白屏且红色叉
如上图所示,xrdp登录出现了红色叉加白屏,这是因为不正常关闭导致,解决方法其实挺简单的 #进入/usr/tmp cd /usr/tmp #删除对应用户的kdecache-** 文件(我这里使用的是kde桌面),例如删除ywj用户对应的文件 …...
Docker安装 Mysql 8.x 版本
文章目录 Docker安装 Mysql 8.0.22Mysql 创建账号并授权Mysql 数据迁移同版本数据迁移跨版本数据迁移 Mysql 5.x 版本与 Mysql 8.x版本是两个大版本,这里演示安装Mysql 8.x版本 Docker安装 Mysql 8.0.22 # 下载mysql $ docker pull mysql 默认安装最新…...

【数理知识】刚体 rigid body 及刚体的运动
文章目录 1 刚体2 刚体一般运动1 平移运动2 旋转运动 Ref 1 刚体 刚体是指在运动中和受力作用后,形状和大小不变,而且内部各点的相对位置不变的物体。绝对刚体实际上是不存在的,只是一种理想模型,因为任何物体在受力作用后&#…...
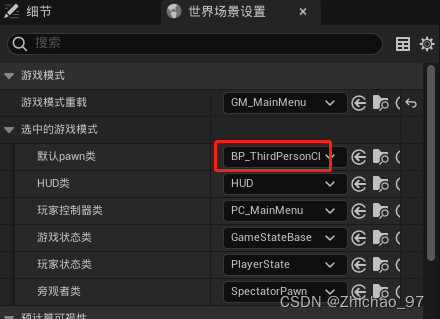
【UE5 多人联机教程】03-创建游戏
效果 步骤 打开“UMG_MainMenu”,增加创建房间按钮的点击事件 添加如下节点 其中,“FUNL Fast Create Widget”是插件自带的函数节点,内容如下: “创建会话”节点指游戏成功创建一个会话后,游戏的其他实例即可发现&am…...

【时间序列预测 】M4
【时间序列预测 】M4 论文题目:The M4 Competition: 100,000 time series and 61 forecasting methods 中文题目: 论文链接: 论文代码: 论文团队: 发表时间: DOI: 引用: 引用数: 摘要…...
:微信小程序授权登录增加多租户可配置界面)
SpringCloud微服务实战——搭建企业级开发框架(五十三):微信小程序授权登录增加多租户可配置界面
GitEgg框架集成weixin-java-miniapp工具包以实现微信小程序相关接口调用功能,weixin-java-miniapp底层支持多租户扩展。每个小程序都有唯一的appid,weixin-java-miniapp的多租户实现并不是以租户标识TenantId来区分的,而是在接口调用时&#…...

Stability AI推出Stable Diffusion XL 1.0,文本到图像模型
Stability AI宣布推出Stable Diffusion XL 1.0,这是一个文本到图像的模型,该公司将其描述为迄今为止“最先进的”版本。 Stability AI表示,SDXL 1.0能生成更加鲜明准确的色彩,在对比度、光线和阴影方面做了增强,可生成…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
