使用EM算法完成聚类任务
EM算法(Expectation-Maximization Algorithm)是一种基于迭代优化的聚类算法,用于在无监督的情况下将数据集分成几个不同的组或簇。EM算法是一种迭代算法,包含两个主要步骤:期望步骤(E-step)和最大化步骤(M-step)。
在EM算法中,假设我们有一个数据集,但是我们不知道数据集中的数据是如何分布的。我们希望将这个数据集分成K个不同的簇,其中每个簇代表一种不同的数据分布。每个簇都由其均值和协方差矩阵表示。EM算法的主要思想是:在开始时随机地初始化这些簇,然后通过E-step和M-step交替迭代来优化簇的均值和协方差矩阵,直到收敛。
具体来说,EM算法的工作原理如下:
-
初始化:随机选择K个中心点作为初始的簇中心,并计算它们的均值和协方差矩阵。
-
E-step:对于每个数据点,计算其属于每个簇的概率(即责任因子),根据这些概率对每个点进行分组。
-
M-step:对于每个簇,使用加权最小二乘法计算其新的均值和协方差矩阵。
-
重复E-step和M-step,直到收敛(即责任因子和中心点的变化小于预定义的阈值)。
-
输出最终的簇中心和它们对应的均值和协方差矩阵,以及每个数据点所属的簇。
使用EM算法完成王者荣耀英雄聚类任务
上面介绍了EM 算法的概念,接下来看个简单的Demo代码,下面的Demo代码是读取原始的csv文件数据,然后使用EM算法进行聚类处理。该文件中记录了不同的hero在最大生命、生命长度等特征上的值。可以看到Demo代码中主要是三个步骤,步骤一:通过热力图选取部分特性,实际就是降纬处理,步骤二:对数据进行归一化处理,步骤三:创建GaussianMixture,传入数据进行无监督训练,然后输出分类结果。
# -*- coding: utf-8 -*-
import pandas as pd
import csv
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import StandardScaler# 数据加载,避免中文乱码问题
data_ori = pd.read_csv('./em/heros.csv', encoding='gb18030')
features = [u'最大生命', u'生命成长', u'初始生命', u'最大法力', u'法力成长', u'初始法力', u'最高物攻', u'物攻成长',u'初始物攻', u'最大物防', u'物防成长', u'初始物防', u'最大每5秒回血', u'每5秒回血成长', u'初始每5秒回血',u'最大每5秒回蓝', u'每5秒回蓝成长', u'初始每5秒回蓝'
]
data = data_ori[features]# 对英雄属性之间的关系进行可视化分析
# 设置 plt 正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 用热力图呈现 features_mean 字段之间的相关性
corr = data[features].corr()
plt.figure(figsize=(14, 14))
# annot=True 显示每个方格的数据
sns.heatmap(corr, annot=True)
plt.show()# 相关性大的属性保留一个,因此可以对属性进行降维
features_remain = [u'最大生命', u'初始生命', u'最大法力', u'最高物攻', u'初始物攻', u'最大物防', u'初始物防', u'最大每5秒回血',u'最大每5秒回蓝', u'初始每5秒回蓝'
]
data = data_ori[features_remain]
# data[u'最大攻速'] = data[u'最大攻速'].apply(lambda x: float(x.strip('%')) / 100)
# data[u'攻击范围'] = data[u'攻击范围'].map({'远程': 1, '近战': 0})
# 采用 Z-Score 规范化数据,保证每个特征维度的数据均值为 0,方差为 1
ss = StandardScaler()
data = ss.fit_transform(data)
# 构造 GMM 聚类
gmm = GaussianMixture(n_components=30, covariance_type='full')
gmm.fit(data)
# 训练数据
prediction = gmm.predict(data)
print(prediction)
# 将分组结果输出到 CSV 文件中
data_ori.insert(0, '分组', prediction)
data_ori.to_csv('./hero_out.csv', index=False, sep=',')from sklearn.metrics import calinski_harabaz_scoreprint(calinski_harabaz_score(data, prediction))
下图是分类后的结果,详细信息如下所示:

在上面的Demo代码中使用到了GaussianMixture方法,该方法是一个用于拟合高斯混合模型(GMM)的类,Demo代码中传入了分类的数量和协方差类型。该方法实际包含很多输入参数,各个参数含义如下所示:
n_components:GMM中的分类数量,默认为1。covariance_type:GMM中各个分量的协方差类型。可选的值为"full"(完全协方差矩阵)、"tied"(相同的协方差矩阵)、"diag"(对角协方差矩阵)和"spherical"(各向同性的协方差矩阵)。默认为"full"。tol:EM算法的收敛容差,默认为1e-3。reg_covar:协方差矩阵对角线上的正则化参数。该参数用于确保协方差矩阵是半正定的,以避免数值计算的问题。默认为0。max_iter:EM算法的最大迭代次数,默认为100。n_init:使用不同的初始化策略进行训练的次数。模型将选择具有最佳性能的初始化策略。默认为1。init_params:用于控制初始化策略的参数。默认为"kmeans",表示使用K-Means算法初始化GMM的均值和协方差矩阵,也可以设置为一个元组,例如("random",{"means": means_init, "covars": covars_init}),表示使用随机值初始化GMM的均值和协方差矩阵。weights_init:GMM各个分量的权重初始化值。默认为None,表示使用初始化策略(即init_params)来初始化权重。means_init:GMM各个分量的均值初始化值。默认为None,表示使用初始化策略(即init_params)来初始化均值。precisions_init:GMM各个分量的协方差矩阵的逆矩阵初始化值。默认为None,表示使用初始化策略(即init_params)来初始化协方差矩阵。random_state:控制随机数生成器的种子,以便在多次运行中得到相同的结果。默认为None。warm_start:如果为True,则使用上一次拟合的结果作为初始化值,并继续从上一次停止的地方训练。默认为False。verbose:控制训练过程中的详细程度。默认为0,表示不输出任何信息。verbose_interval:控制训练过程中输出信息的频率。默认为10,表示每迭代10次输出一次信息。
上面的init_params参数控制初始化策略,默认是kmeans,即用K-Means算法初始化GMM的均值和协方差矩阵,前面介绍过K-Means算法,该算法也可以完成聚类任务,那么EM算法和K-means算法有什么区别呢?
EM算法与K-Means算法区别
-
簇形状:K-means算法假定每个簇都是由一个中心点和周围的数据点组成的球形簇,而EM算法则假定每个簇可以由任意形状的高斯分布表示。
-
簇数量:在K-means算法中,需要预先指定要划分的簇数量K,而在EM算法中则不需要预先指定,可以自动确定最佳的簇数。
-
算法原理:K-means算法通过计算每个数据点到簇中心的距离,将数据点分配到最近的簇中。而EM算法则是基于最大似然估计,利用期望最大化算法(Expectation-Maximization Algorithm)来优化簇的均值和协方差矩阵。
-
鲁棒性:K-means算法对离群点非常敏感,因为它使用平方误差和来计算距离,而EM算法则对离群点的影响较小,因为它使用高斯分布模型来建模每个簇。
-
数据类型:K-means算法适用于数值型数据,而EM算法也适用于混合数据类型,比如文本和图像数据。
-
算法复杂度:K-means算法的时间复杂度为O(nki),其中n是数据点的数量,k是簇的数量,i是迭代次数。而EM算法的时间复杂度通常比K-means算法更高,因为它需要估计每个簇的均值和协方差矩阵,这通常需要更多的计算量。
总的来说,EM算法和K-means算法都是用于无监督的聚类问题的算法。但K-means算法更简单,更快速,对于非球形簇和离群点的处理不如EM算法。EM算法更灵活,能够处理更多的数据类型和簇形状,但是通常需要更多的计算时间。
相关文章:

使用EM算法完成聚类任务
EM算法(Expectation-Maximization Algorithm)是一种基于迭代优化的聚类算法,用于在无监督的情况下将数据集分成几个不同的组或簇。EM算法是一种迭代算法,包含两个主要步骤:期望步骤(E-step)和最…...

❤️创意网页:创意视觉效果粒子循环的网页动画
✨博主:命运之光 🌸专栏:Python星辰秘典 🐳专栏:web开发(简单好用又好看) ❤️专栏:Java经典程序设计 ☀️博主的其他文章:点击进入博主的主页 前言:欢迎踏入…...

【MTI 6.S081 Lab】thread
【MTI 6.S081 Lab】thread 前言调度Uthread: switching between threads (moderate)实验任务Hints解决方案thread_switchthread_create()thread_schedule() Using threads (moderate)实验任务解决方案 Barrier (moderate)实验任务解决方案 本实验前去看《操作系统导论》第29章基…...

AWS / VPC 云流量监控
由于安全性、数据现代化、增长、灵活性和成本等原因促使更多企业迁移到云,将数据存储在本地的组织正在使用云来存储其重要数据。亚马逊网络服务(AWS)仍然是最受追捧和需求的服务之一,而亚马逊虚拟私有云(VPC࿰…...

【C++学习笔记】extern “c“以及如何查看符号表
如何查看符号表 要查看.a文件的内容,可以使用ar命令。下面是一些常见的用法: 列出.a文件中包含的所有文件: ar t <filename.a>提取.a文件中的单个文件: ar x <filename.a> <filename.o>将.a文件中的所有文件提…...
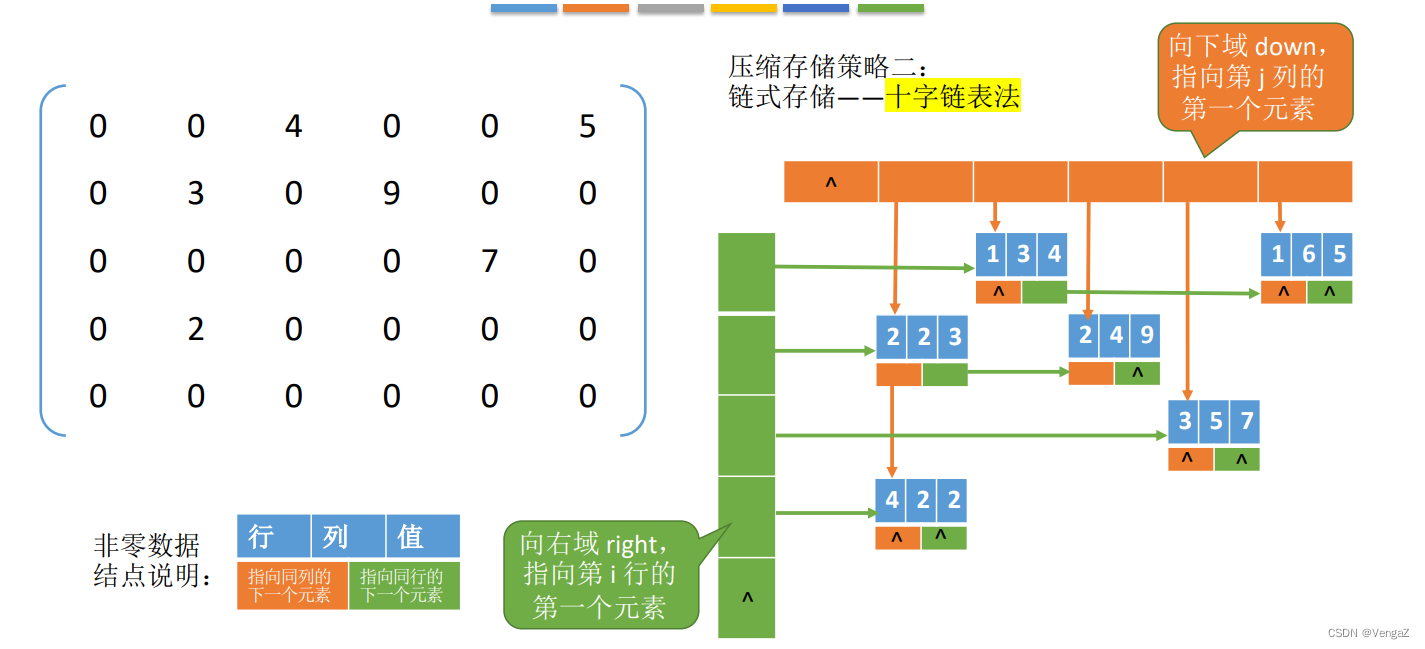
24考研数据结构-数组和特殊矩阵
目录 数据结构:数组与特殊矩阵数组数组的特点数组的用途 特殊矩阵对角矩阵上三角矩阵和下三角矩阵稀疏矩阵特殊矩阵的用途 结论 3.4 数组和特殊矩阵3.4.1数组的存储结构3.4.2普通矩阵的存储3.4.3特殊矩阵的存储1. 对称矩阵(方阵)2. 三角矩阵(方阵)3. 三对角矩阵(方阵…...

服务器后台运行程序
代码运行 要让代码在服务器后台运行,有多种方法。在 Linux 系统中,最常见的有以下几种方式: **1. 使用 & 符号:** 在命令后面添加 & 符号可以让程序在后台运行。例如: bash python myscript.py &但是…...
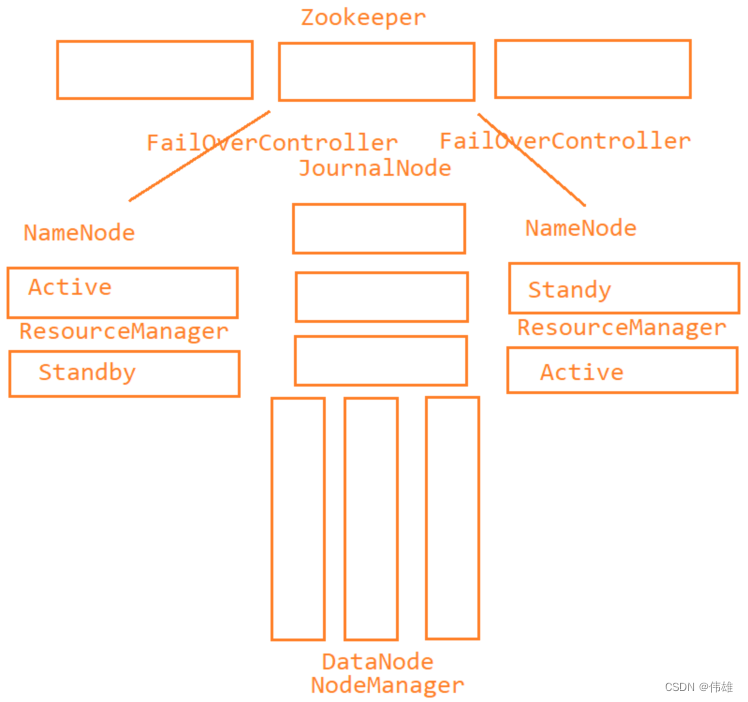
大数据课程D7——hadoop的YARN
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解YARN的概念和结构; ⚪ 掌握YARN的资源调度流程; ⚪ 了解Hadoop支持的资源调度器:FIFO、Capacity、Fair; ⚪ 掌握YA…...

Rust vs Go:常用语法对比(十三)
题图来自 Go vs. Rust: The Ultimate Performance Battle 241. Yield priority to other threads Explicitly decrease the priority of the current process, so that other execution threads have a better chance to execute now. Then resume normal execution and call f…...

【【51单片机DA转换模块】】
爆改直流电机,DA转换器 main.c #include <REGX52.H> #include "Delay.h" #include "Timer0.h"sbit DAP2^1;unsigned char Counter,Compare; //计数值和比较值,用于输出PWM unsigned char i;void main() {Timer0_Init();whil…...

[SQL挖掘机] - 字符串函数 - substring
介绍: substring函数是在mysql中用于提取字符串的一种函数。它接受一个字符串作为输入,并返回从该字符串中指定位置开始的一部分子串。substring函数可以用于获取字符串中的特定字符或子串,以便进行进一步的处理或分析。 用法: 下面是substring函数的…...
第一百一十六天学习记录:C++提高:STL-string(黑马教学视频)
string基本概念 string是C风格的字符串,而string本质上是一个类 string和char区别 1、char是一个指针 2、string是一个类,类内部封装了char*,管理这个字符串,是一个char型的容器。 特点: string类内部封装了很多成员方…...
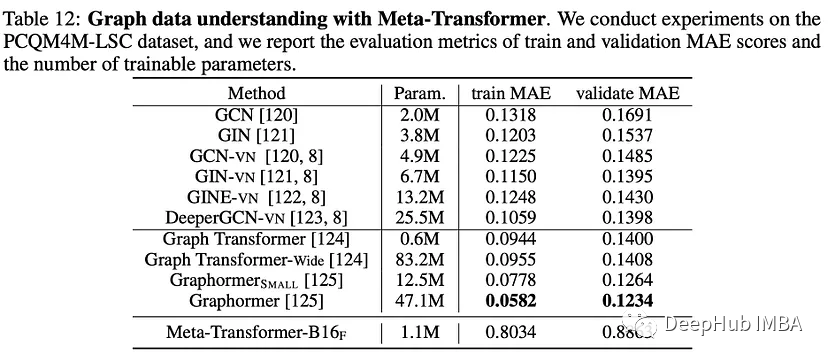
Meta-Transformer 多模态学习的统一框架
Meta-Transformer是一个用于多模态学习的新框架,用来处理和关联来自多种模态的信息,如自然语言、图像、点云、音频、视频、时间序列和表格数据,虽然各种数据之间存在固有的差距,但是Meta-Transformer利用冻结编码器从共享标记空间…...
tinkerCAD案例:24.Tinkercad 中的自定义字体
tinkerCAD案例:24.Tinkercad 中的自定义字体 原文 Tinkercad Projects Tinkercad has a fun shape in the Shape Generators section that allows you to upload your own font in SVG format and use it in your designs. I’ve used it for a variety of desi…...
list与流迭代器stream_iterator
运行代码: //list与流迭代器 #include"std_lib_facilities.h" //声明Item类 struct Item {string name;int iid;double value;Item():name(" "),iid(0),value(0.0){}Item(string ss,int ii,double vv):name(ss),iid(ii),value(vv){}friend ist…...

九耶:冯·诺伊曼体系
冯诺伊曼体系(Von Neumann architecture)是一种计算机体系结构,它由匈牙利数学家冯诺伊曼于1945年提出。冯诺伊曼体系是现代计算机体系结构的基础,几乎所有的通用计算机都采用了这种体系结构。 冯诺伊曼体系的核心思想是将计算机硬…...
探索UCI心脏病数据:利用R语言和h2o深度学习构建预测模型
一、引言 随着机器学习模型在实际应用中的广泛应用,人们对于模型的解释性和可理解性日益关注。可解释性机器学习是指能够清晰、透明地解释机器学习模型决策过程的一种方法和技术。在许多领域中,如医疗诊断、金融风险评估和自动驾驶等,解释模型…...
基于 moleculer 微服务架构的智能低代码PaaS 平台源码 可视化开发
低代码开发平台源码 低代码管理系统PaaS 平台 无需代码或通过少量代码就可以快速生成应用程序的开发平台。 本套低代码管理后台可以支持多种企业应用场景,包括但不限于CRM、ERP、OA、BI、IoT、大数据等。无论是传统企业还是新兴企业,都可以使用管理后台…...

xrdp登录显示白屏且红色叉
如上图所示,xrdp登录出现了红色叉加白屏,这是因为不正常关闭导致,解决方法其实挺简单的 #进入/usr/tmp cd /usr/tmp #删除对应用户的kdecache-** 文件(我这里使用的是kde桌面),例如删除ywj用户对应的文件 …...
Docker安装 Mysql 8.x 版本
文章目录 Docker安装 Mysql 8.0.22Mysql 创建账号并授权Mysql 数据迁移同版本数据迁移跨版本数据迁移 Mysql 5.x 版本与 Mysql 8.x版本是两个大版本,这里演示安装Mysql 8.x版本 Docker安装 Mysql 8.0.22 # 下载mysql $ docker pull mysql 默认安装最新…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
