贪心算法总结及其leetcode题目N道
1 我为什么要写这个总结
1.1 字节笔试题
小明在玩一场通关游戏,初始血量为1,关卡有怪兽或者有血包(正数就是血包可回血数,负数说明是怪兽的伤害值),当捡到血包时会加血量,碰到怪兽时会掉血,现在指定初始血量为x,关卡是一个数组,小明必须按照数组的顺序玩游戏,当碰到一个怪兽时,他可以选择将这个怪兽扔到数组末尾,小明可以无限次地将怪兽移到数组末尾,问小明最少移动几次就能存活,如果无论怎么移动都不能存活则返回-1, 假设关卡是这样的[-200,-300,400],则返回-1,假如是这样的[200,100,-250,-60,-70,100],则返回1,只需要把-250挪到尾部,
思路:当发现自己血量不足时,就从当前已经遍历过的所有关卡中,选择耗费血量最多的那个关卡并且放到最后一关,如果即使这样挪开了耗血量最大的一关自身血量还是为负,则直接返回-1,说明无法通关
2 总结
2.1 什么是局部最优?
贪心关注的是局部最优,这里当前最优(指当前遍历的所有元素中的最优解)也是局部最优的一种,而一般的最有解又涉及到数据的最值,而且随着元素的不断向右扩展,可能这个最优值是不断变化的,所以一般可以使用堆来动态维护它的最值。
2.2 解贪心类题目的一些分类
分为相向双指针,同向双指针以及最值堆等类型
2.2.1 相向双指针和同向双指针的解题思路的区别
-
相向双指针通常用于处理排序数组中的问题,比如找出两个数的和等于特定值(如LeetCode题目167. 两数之和 II - 输入有序数组),或者反转数组(如LeetCode题目344. 反转字符串)。对于这类问题,两个指针分别从数组的头部和尾部出发,根据指向元素的大小关系向中间移动,直到两个指针相遇。
-
同向双指针通常用于处理数组或字符串中需要连续元素满足特定条件的问题,比如找出满足特定和的最小子数组(如LeetCode题目209. 长度最小的子数组),或者找出最长的满足特定条件的子串(如LeetCode题目424. 替换后的最长重复字符)。对于这类问题,一个指针(快指针)用于遍历数组或字符串,另一个指针(慢指针)用于维护满足条件的区间。
2.2.2 在LeetCode上,与同向双指针和贪心策略相关的题目有很多。举两个例子:
-
题目 209. 长度最小的子数组: 在一个正整数数组中寻找长度最小的连续子数组,其和至少为特定值。解决这个问题的方法是维持一个滑动窗口,窗口的左右边界就是同向的双指针。右指针向右移动以增加子数组的和,当子数组的和达到或超过目标值时,尝试将左指针向右移动以减小子数组的长度。
-
题目 424. 替换后的最长重复字符: 给定一个字符串和一个整数k,找出可以通过最多替换k个字符以得到的最长的重复字符子串。解决这个问题的方法同样是维持一个滑动窗口,窗口的左右边界就是同向的双指针。右指针向右移动以增加子串的长度,当子串中最多的字符数量加上k小于子串的长度时,左指针向右移动。
2.3 一部分需要预处理的题目
2.3.1 可能需要排序
- 分发饼干
2.3.2 可能需要hashMap统计字符最后一次出现的位置
- 划分字母区间
3 使用堆解决问题的贪心策略
3.1 leetcode1046. 最后一块石头的重量
3.2 leetcode 1642. 可以到达的最远建筑
leetcode 1642. 可以到达的最远建筑
标准答案:
// 砖块优先,砖块数量不足时考虑将当前替代最小高度的梯子改用砖块替代public int furthestBuilding(int[] heights, int bricks, int ladders) {int n=heights.length;//大根堆PriorityQueue<Integer>pq=new PriorityQueue<>((o1,o2)->(o2-o1));int i;int sum=0;//表示当前需要的梯子数量int sum_bri=0;for(i=1;i<n;i++){int diff=heights[i]-heights[i-1];if(diff>0){pq.offer(diff);sum_bri+=diff;//砖块的数量之和if(sum_bri>bricks){sum_bri-=pq.poll();sum++;}if(sum>ladders){return i-1;}}}return n-1;}//每次先放梯子,当梯子数量不足时,将当前使用过的梯子中,替代阶梯数最少的梯子找出来用对应砖头替换,替换出来的梯子拿到当前使用public int furthestBuilding(int[] heights, int bricks, int ladders) {int n=heights.length;//int[]:PriorityQueue<Integer>pq=new PriorityQueue<>((o1,o2)->(o1-o2));int i;int sum=0;//表示当前需要的砖块数量for(i=1;i<n;i++){int diff=heights[i]-heights[i-1];if(diff>0){pq.offer(diff);if(pq.size()>ladders){sum+=pq.poll();}if(sum>bricks){return i-1;}}}return n-1;}```我的答案:(有几个特别长的case过不了)```java
public int furthestBuilding2(int[] heights, int bricks, int ladders) {int n=heights.length;PriorityQueue<Integer>pq=new PriorityQueue<>((o1,o2)->(o1-o2));int i;for(i=1;i<n;){int diff=heights[i-1]-heights[i];// System.out.println("i:"+i+",diff:"+diff+",heights[i-1]:"+heights[i-1]+",heights[i]:"+heights[i]);if(diff<0){int diffAbs=-diff;if(ladders>0){ladders--;pq.add(diffAbs);}else if(bricks>=diffAbs){bricks-=diffAbs;}else{int newd=Integer.MAX_VALUE;if(!pq.isEmpty()){newd=pq.peek();}if(bricks>=newd){pq.poll();bricks-=newd;ladders++;i=i-1;}else{break;}}}i++;}return i-1;}
这里还有一个二分查找的方法:
每太整明白:
3.3 121. 买卖股票的最佳时机(虽然使用堆的方法不是最优解,但是方便和其他题目对比得出最优解)
3.3.1 这个题和3.1以及3.2有什么异同呢?
同:都涉及到取最值,而且最值都是可能变化的
不同:3.1以及3.2中的题目一个最值只能使用一次,一旦使用就得poll操作,而本题中的最值可以复用。正式这个特性导致了前者只能使用堆来维护最值(因为可能需要多次取最值,即使用到多个最值,poll操作只能靠堆维护),虽说本题也多次最最值,但是可以重用最值,没有poll操作。
class Solution {// 使用堆维护最小值public int maxProfit(int[] prices) {int n=prices.length;//表示到第i天时,股票的历史最低点价格PriorityQueue<Integer>pq=new PriorityQueue<>((o1,o2)->(o1-o2));int max=0;for(int i=0;i<n;i++){pq.add(prices[i]);max=Math.max(max,prices[i]-pq.peek());}return max;}// 方法:使用dp维护已经遍历值得最小值public int maxProfit3(int[] prices) {int n=prices.length;//表示到第i天时,股票的历史最低点价格int[]f=new int[n];f[0]=prices[0];int max=0;for(int i=1;i<n;i++){f[i]=Math.min(f[i-1],prices[i]);max=Math.max(max,prices[i]-f[i]);}return max;}// 方法:使用一个变量维护已经遍历值得最小值public int maxProfit(int[] prices) {int n=prices.length;//表示到第i天时,股票的历史最低点价格int min=prices[0];int max=0;for(int i=1;i<n;i++){min=Math.min(min,prices[i]);max=Math.max(max,prices[i]-min);}return max;}// 使用单调栈维护已经遍历序列的最小值public int maxProfit2(int[] prices) {int n=prices.length;Deque<Integer>st=new ArrayDeque<>();int max=0;st.add(prices[0]);for(int i=1;i<n;i++){int p=prices[i];if(!st.isEmpty()&&p<=st.peekLast()){max=Math.max(st.peekLast()-st.peekFirst(),max);while(!st.isEmpty()&&st.peekLast()>=p){st.pollLast();}}st.addLast(p);}if(!st.isEmpty()){max=Math.max(st.peekLast()-st.peekFirst(),max);}return max;}
}
3.3 871题最低加油次数和
3.4 630课程表III
4 使用相向双指针解决问题的贪心策略
4.1 167. 两数之和 II - 输入有序数组
思路:双指针解决偏差
class Solution {public int[] twoSum(int[] numbers, int target) {int n=numbers.length;int i=0,j=n-1;while(i<j){int sum=numbers[i]+numbers[j];if(sum>target){j--;}else if(sum<target){i++;}else{return new int[]{i+1,j+1};}}return new int[]{i+1,j+1};}}
4.2 11. 盛最多水的容器
思路:容器能盛的水取决于短板,不断移动双指针中代表较小数值的那个指针,直到两个指针相遇,其中得到的所有可能的盛水量中取最大值即可。
class Solution {public int maxArea(int[] height) {int n=height.length;int i=0,j=n-1;int max=-1;while(i<j){int s=(j-i)*Math.min(height[i],height[j]);max=Math.max(max,s);if(height[i]>height[j]){j--;}else{i++;}}return max;}
}
5 同向双指针与贪心策略
5.1 763. 划分字母区间(找出数组中满足特定条件的子序列)
class Solution {public List<Integer> partitionLabels(String s) {int n=s.length();int[]mp=new int[26];for(int i=0;i<n;i++){mp[s.charAt(i)-'a']=i;}List<Integer>res=new ArrayList<>();int start=0,end=0;for(int i=0;i<n;i++){end=Math.max(end,mp[s.charAt(i)-'a']);if(end==i){res.add(i-start+1);start=i+1;}}return res;}
}
相关文章:

贪心算法总结及其leetcode题目N道
1 我为什么要写这个总结 1.1 字节笔试题 小明在玩一场通关游戏,初始血量为1,关卡有怪兽或者有血包(正数就是血包可回血数,负数说明是怪兽的伤害值),当捡到血包时会加血量,碰到怪兽时会掉血&am…...

k8s的namespace一直处于terminating的解法
先试了强制替换,无法替换掉,强制删除,也删除不掉namespace [rootmaster k8s-study]# vi ns-demo.yaml [rootmaster k8s-study]# kubectl create -f ns-demo.yaml namespace/demo created [rootmaster k8s-study]# kubectl get -f ns-demo.ya…...

JAVA面试总结-Redis篇章(六)——数据过期策略
Java面试总结-Redis篇章(六)——数据过期策略 Redis数据删除策略——惰性删除Redis数据删除策略——定期删除 Redis数据删除策略——惰性删除 Redis数据删除策略——定期删除...
【LLM】大语言模型学习之LLAMA 2:Open Foundation and Fine-Tuned Chat Model
大语言模型学习之LLAMA 2:Open Foundation and Fine-Tuned Chat Model 快速了解预训练预训练模型评估微调有监督微调(SFT)人类反馈的强化学习(RLHF)RLHF结果局限性安全性预训练的安全性安全微调上手就干使用登记代码下载获取模型转换模型搭建Text-Generation-WebUI分发模型…...

Android是如何识别USB信号的
Android设备通过USB接口与外部设备通信时,会通过USB控制器(USB Controller)与USB设备进行通信。USB控制器是Android设备的一个硬件组件,它负责管理USB总线并控制所有USB设备的连接和通信。 当一个USB设备被插入Android设备的USB接…...

机器学习前言
1.机器学习和统计学关系 2.机器学习的发展 3.机器学习与深度学习的相同点与不同点 4.机器学习和深度学习优缺点 一、机器学习和统计学关系 机器学习和统计学密切相关,可以说机器学习是统计学在计算机科学和人工智能领域的应用。机器学习和统计学在方法论和技术上有…...
Java另一种debug方法(not remote jmv debug),类似python远程debug方式
这种Debug类似python的debug方式,是运行时将业务代码及依赖推送到Linux并使用Linux的java运行运行程。只要本地能运行,就能自动将代码推送到Linux运行,不需打包及设置远程debug jvm参数,适合一些项目Debug调试 运行时会推送一些依…...
【QT】Day4
1> 思维导图 2> 手动完成服务器的实现,并具体程序要注释清楚 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTcpServer> //服务器类 #include <QTcpSocket> //客户端类 #include <QMessageBox> //…...
)
在CSDN学Golang云原生(Kubernetes Pod 有状态部署)
一,StatefulSet部署MongoDB集群 Kubernetes StatefulSet 是 Kubernetes 中的一种资源类型,它能够保证有状态服务(Stateful Service)的唯一性和顺序部署,适用于需要持久化存储、网络标识、状态管理等场景。MongoDB 是一…...

sql-从一个或多个表中向一个表中插入 多行
INSERT还可以将SELECT语句查询的结果插入到表中,此时不需要把每一条记录的值一个一个输入,只需 要使用一条INSERT语句和一条SELECT语句组成的组合语句即可快速地从一个或多个表中向一个表中插入 多行。 基本语法格式如下: INSERT INTO 目标表…...

ElementUI 实现动态表单数据校验(已解决)
文章目录 🍋前言:🍍正文1、探讨需求2、查阅相关文档([element官网](https://element.eleme.cn/#/zh-CN/component/form))官方动态增减表单项示例3、需求完美解决4、注意事项 🎃专栏分享: &#…...
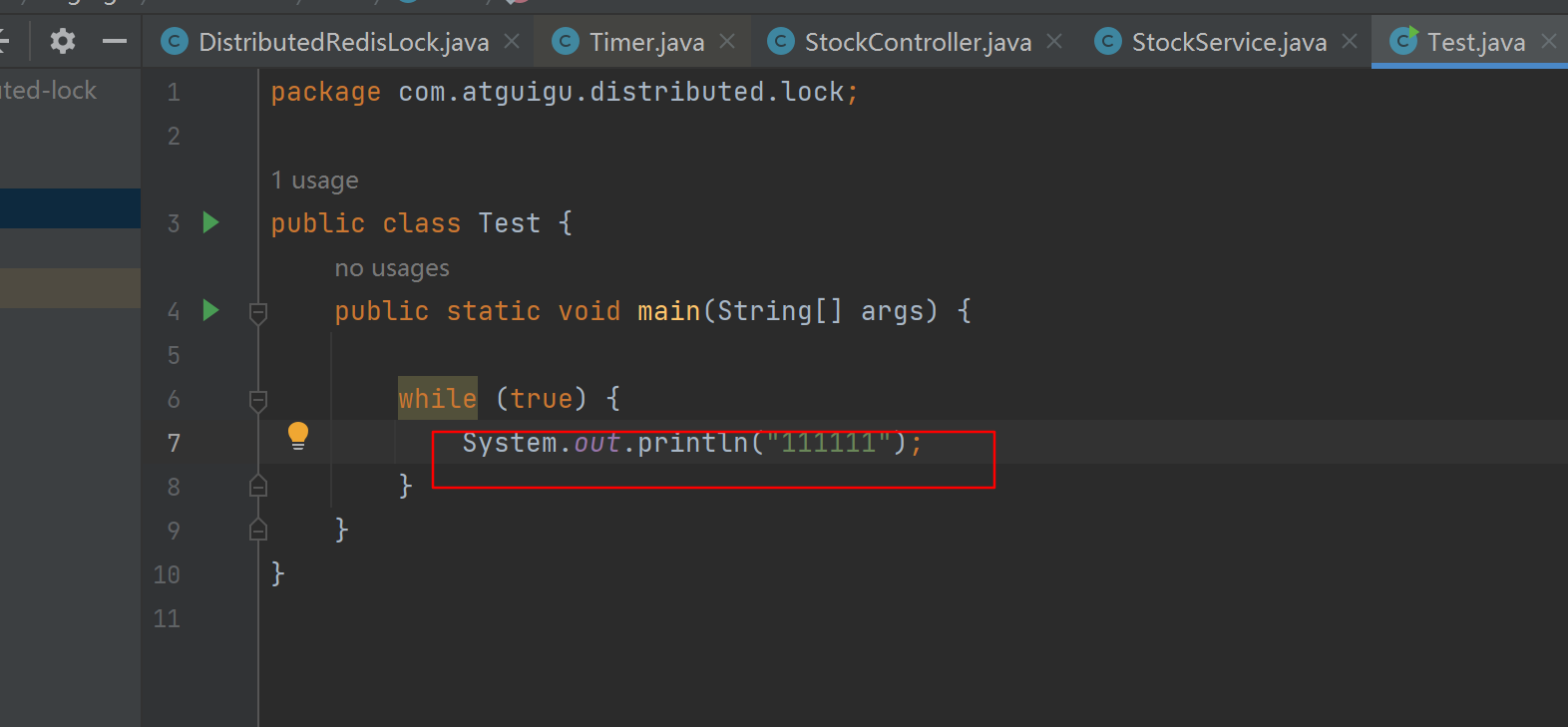
Linux上定位线上CPU飙高
【模拟场景】 写一个java main函数,死循环打印 System.out.println(“111111”) , 将其打成jar包放在linux中执行 1、通过TOP命令找到CPU耗用最厉害的那个进程的PID 2、top -H -p 进程PID 找到进程下的所有线程 可以看到 pid 为 94384的线程耗用cpu …...

06-行向量列向量_向量的运算 加法,数乘,减法,转置
行向量和列向量 行向量是按行把向量排开(横着来写), 列向量是按列把向量排开(竖着来写) 在数学中我们更多的把数据写成列向量,在编程语言中更多的把数据存成行向量! 如果想在编程语言中把行向量转化成列…...
)
基于Matlab实现最大类间方差阈值与遗传算法的道路分割(附上完整源码+图像+程序运行说明)
道路分割是计算机视觉和图像处理中的一个重要任务,它在交通监控、自动驾驶和地图制作等领域具有广泛的应用。其中,最大类间方差阈值和遗传算法是道路分割中常用的方法之一。本文将介绍如何使用Matlab实现最大类间方差阈值与遗传算法进行道路分割。 文章目…...

13.4.2 【Linux】sudo
相对于 su 需要了解新切换的使用者密码 (常常是需要 root 的密码), sudo 的执行则仅需要自己的密码即可。sudo 可以让你以其他用户的身份执行指令 (通常是使用 root 的身份来执行指令),因此并非所有人都能够…...

电脑软件:键盘按键修改器——keytweak使用介绍
对你的电脑键盘的布局不满意、键盘上的某个按键坏掉了等等键盘问题如何解决?有了KeyTweak这一切就可以轻松解决了,KeyTweak是一个免费软件程序,使用它可让你重新映射键盘键。如果您改变主意并想将其改回原样,只需点击一下即可容易…...

软件工程学术顶会——ICSE 2023 议题(网络安全方向)清单与摘要
按语:IEEE/ACM ICSE全称International Conference on Software Engineering,是软件工程领域公认的旗舰学术会议,中国计算机学会推荐的A类国际学术会议,Core Conference Ranking A*类会议,H5指数74,Impact s…...

【Python】jupyter Linux服务器使用
文章目录 环境使用访问 环境 pip install jupyter 使用 在你想访问的目录下执行: jupyter notebook --ip0.0.0.0jupyter 给出提示: [I 2023-07-28 14:32:43.589 ServerApp] Package notebook took 0.0000s to import [I 2023-07-28 14:32:43.597 Ser…...
element 级联 父传子
html代码例子 父组件 <el-cascaderstyle"width: 100%"change"unitIdChange":options"unitOptions"filterablev-model"formInline.unitId":props"unitProps"/></el-form-item>//改变级联传值到这个组件里面<r…...

【MTI 6.S081 Lab】Copy-on-write
【MTI 6.S081 Lab】Copy-on-write The problemThe solutionImplement copy-on-write fork (hard)实验任务Hints解决方案问题解决思考uvmcopykfreekallockpagerefcow_handlertrap 虚拟内存提供了一定程度的间接性:内核可以通过将PTE标记为无效或只读来拦截内存引用&a…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
