Pycharm debug程序,跳转至指定循环条件/循环次数
在断点出右键,然后设置条件

示例
for i in range(1,100):a = i + 1b = i + 2print(a, b, i)注意:
1、你应该debug断点在循环后的位置而不是循环上的位置,然后你就可以设置你的条件进入到指定的循环上了

2、设置条件,要使用等于符号“==”而不是赋值符号“=”
3、在设置断点条件的位置,条件应该是出现过的变量,例如下面设置“a==15”是正确的、“b==15”就是错误的,因为b在这一行运行之前还没有出现

在运行过程中设置条件,从而直接运行到这次的条件循环,而不需要重新debug
例如此时你设置了断点,但是没有设置断点条件,此时i=1是第一次循环

此时你想调到第15次循环,也就是条件“I==15”,那么你不需要重新debug,而只需要在本次运行中设置循环条件,然后直接“Step out”就可以了【Shift + F8】

成功进入第15次循环:

相关文章:

Pycharm debug程序,跳转至指定循环条件/循环次数
在断点出右键,然后设置条件 示例 for i in range(1,100):a i 1b i 2print(a, b, i) 注意: 1、你应该debug断点在循环后的位置而不是循环上的位置,然后你就可以设置你的条件进入到指定的循环上了 2、设置条件,要使用等于符号…...

react实现markdown
参考:https://blog.csdn.net/Jack_lzx/article/details/118495763 参考:https://blog.csdn.net/m0_48474585/article/details/119742984 0. 示例 用react实现markdown编辑器 1.基本布局及样式 <><div classNametf_editor_header>头部&…...
HTTP请求走私漏洞简单分析
文章目录 HTTP请求走私漏洞的产生HTTP请求走私漏洞的分类HTTP请求走私攻击的危害确认HTTP请求走私漏洞通过时间延迟技术确认CL漏洞通过时间延迟技术寻找TE.CL漏洞 使用差异响应内容确认漏洞通过差异响应确认CL.TE漏洞通过差异响应确认TE.CL漏洞 请求走私漏洞的利用通过请求漏洞…...
BI-SQL丨两表差异比较
BOSS:哎,白茶,我们最近新上了一个系统,后续有一些数据要进行源切换,这个能整么? 白茶:没问题,可以整! BOSS:哦,对了,差点忘记告诉你了…...

ZooKeeper 选举的过半机制防止脑裂
结论: Zookeeper采用过半选举机制,防止了脑裂。 原因: 如果有5台节点,leader联系不上了,其他4个节点由于超过半数,所以又选出了一个leader,当失联的leader恢复网络时,发现集群中已…...
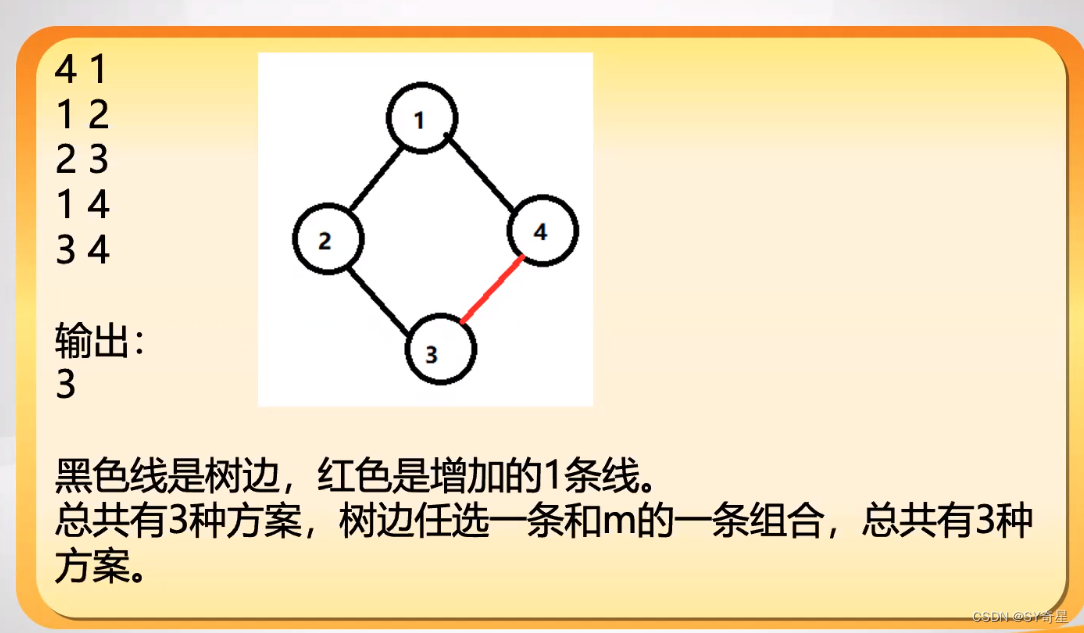
【图论】树上差分(边差分)
一.简介 其实点差分和边差分区别不大。 点差分中,d数组存储的是树上的节点 边差分中,d数组存储的是当前节点到父节点的那条边的差分值。 指定注意的是:边差分中因为根连的父节点是虚点,所以遍历结果时应当忽略! 二…...
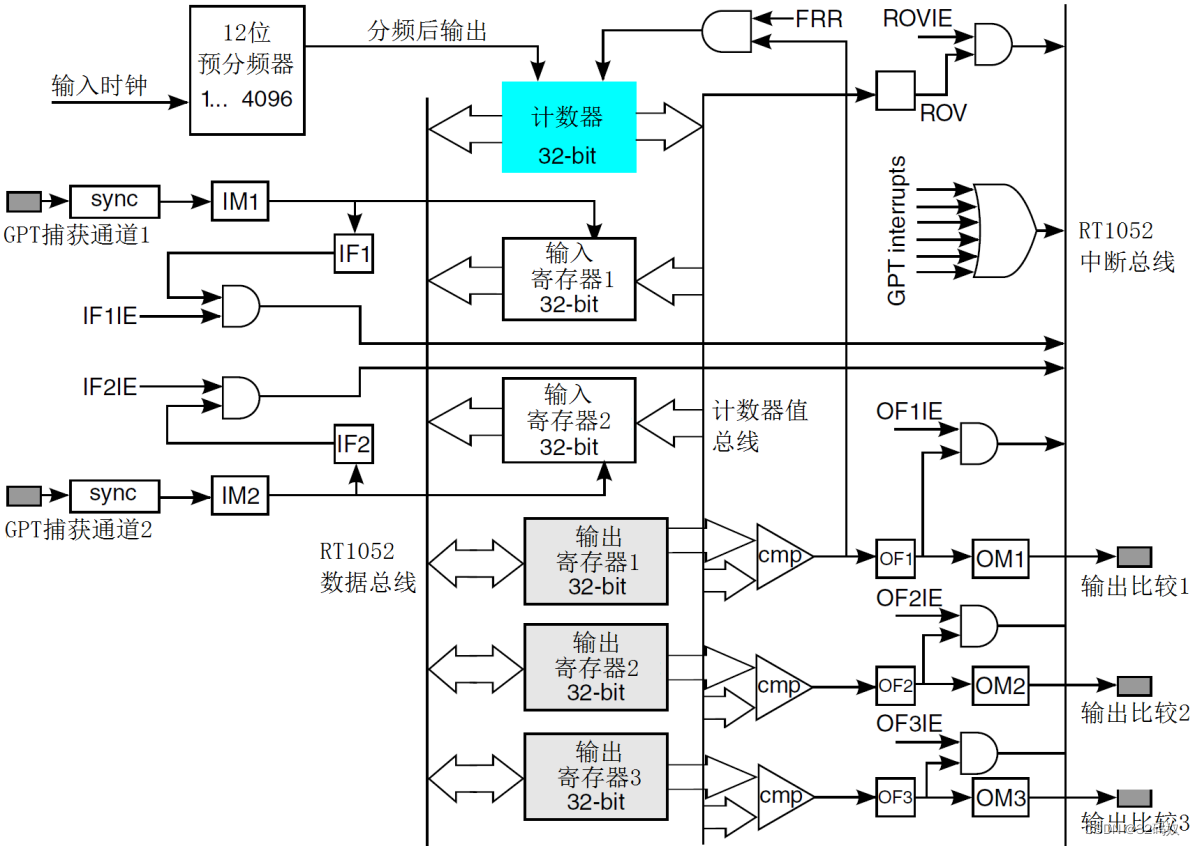
RT1052的定时器
文章目录 1 通用定时器1.1 定时器框图1.2 实现周期性中断 2 相关寄存器3 定时器配置3.1 时钟使能3.2 初始化GPT1定时器3.2.1 base3.2.2 initConfig3.2.2.1 clockSorce3.2.2.2 divider3.2.2.3 enablexxxxx 3.3 设置 GPT1 比较值3.3.1 base3.3.2 channel3.3.3 value 3.4 设置 GPT…...
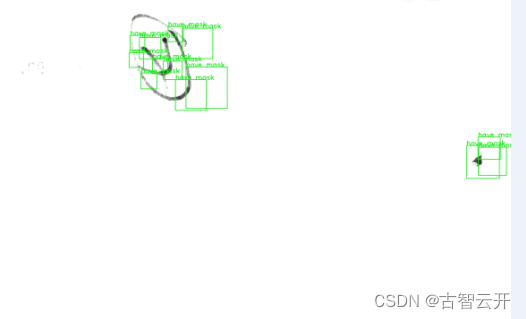
opencv python 训练自己的分类器
源码下载 一、分类器制作 1.样本准备 收集好你所需的正样本,和负样本,分别保存在不同文件夹 在pycharm新建项目,项目结构如下:has_mask文件夹放置正样本,no_mask文件夹放置负样本 安装opencv,把opencv包…...
详解Mybatis之分页插件【PageHelper】
编译软件:IntelliJ IDEA 2019.2.4 x64 操作系统:win10 x64 位 家庭版 Maven版本:apache-maven-3.6.3 Mybatis版本:3.5.6 文章目录 一. 什么是分页?二. 为什么使用分页?三. 如何设计一个Page类(分…...
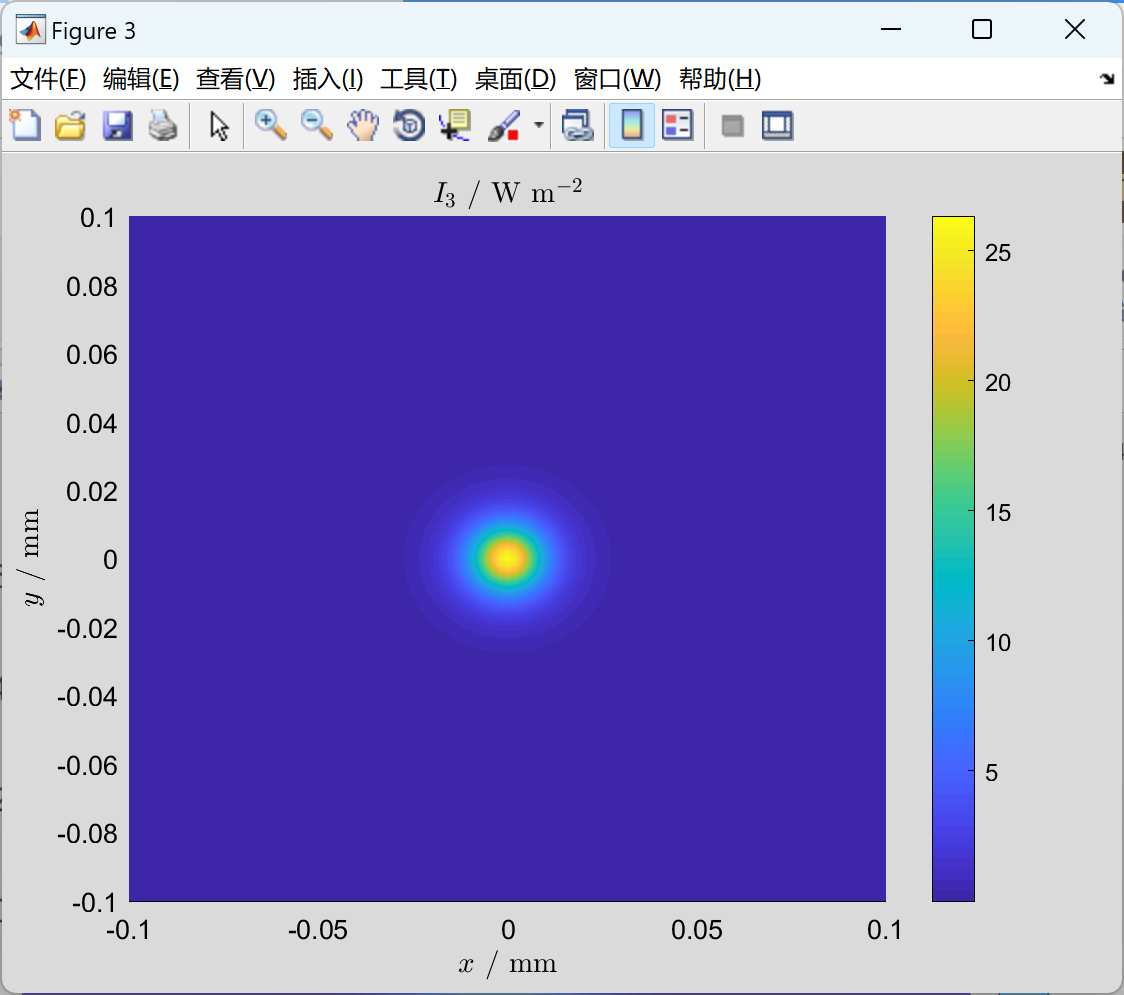
【基于矢量射线的衍射积分 (VRBDI)】基于矢量射线的衍射积分 (VRBDI) 和仿真工具(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

基于jackson对bean的序列号和反序列化
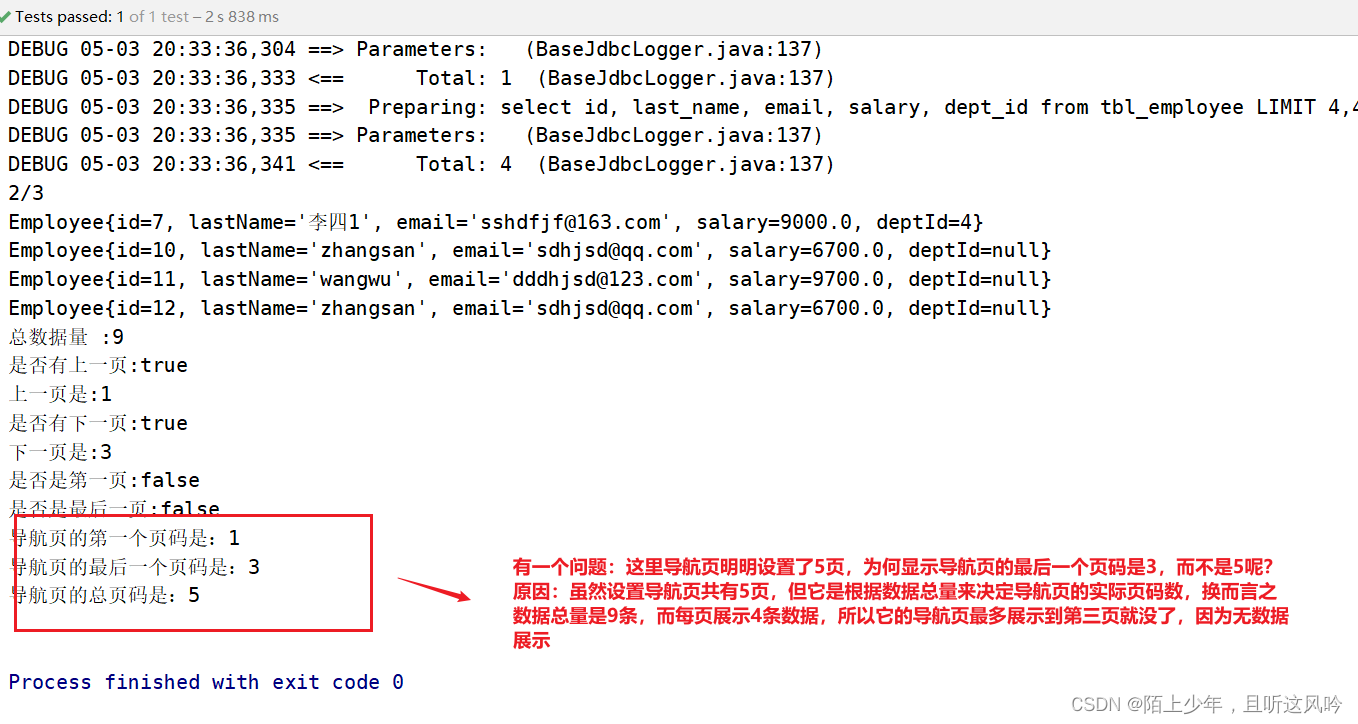
通过观察控制台输出的SQL发现页面传递过来的员工id的值和数据库中的id值不一致,这是怎么回事呢? 分页查询时服务端响应给页面的数据中id的值为19位数字,类型为long 页面中js处理long型数字只能精确到前16位,所以最终通过ajax请求提交给服务…...

排队理论简介
排队理论简介 1. 理论背景2. 研究的数学方法3. 拒绝型排队系统与等候型排队系统4. 拒绝型排队系统 本文参考文献为Вентцель Е. С.的《Исследование операций》。 1. 理论背景 排队理论又称大众服务理论,顾名思义指的是在有限的服务条…...
-算法分析)
极速查找(3)-算法分析
篇前小言 本篇文章是对查找(2)的续讲二叉排序树 二叉排序树(Binary Search Tree,BST),又称为二叉查找树,是一种特殊的二叉树。性质: 左子树的节点值小于根节点的值,右…...

http 常见的响应状态码 ?
100——客户必须继续发出请求101——客户要求服务器根据请求转换HTTP协议版本200——交易成功201——提示知道新文件的URL202——接受和处理、但处理未完成203——返回信息不确定或不完整204——请求收到,但返回信息为空205——服务器完成了请求,用户代理…...
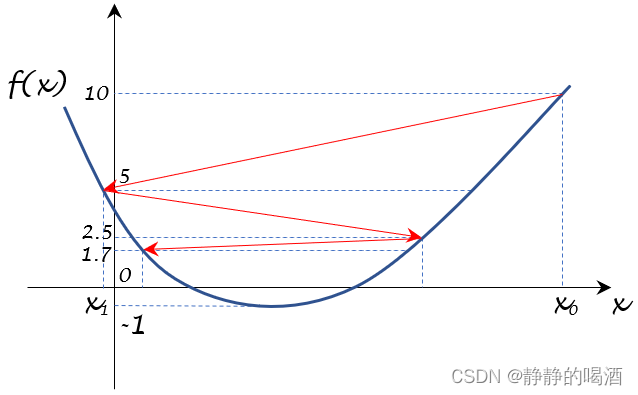
机器学习笔记之优化算法(四)线搜索方法(步长角度;非精确搜索)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索] 引言回顾:精确搜索步长及其弊端非精确搜索近似求解最优步长的条件反例论述 引言 上一节介绍了从精确搜索的步长角度观察了线搜索方法,本节将从非精确搜索的步长角度重新观察线搜…...
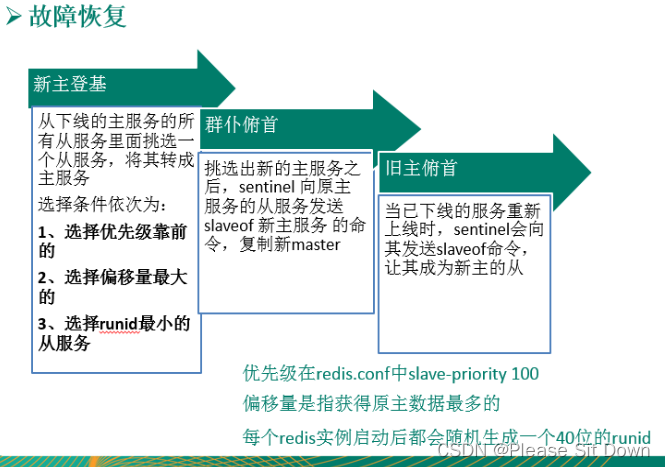
Redis 哨兵 (sentinel)
是什么 官网理论:https://redis.io/docs/management/sentinel/ 吹哨人巡查监控后台 master 主机是否故障,如果故障了根据投票数自动将某一个从库转换为新主库,继续对外服务。 作用:无人值守运维 哨兵的作用: 1…...

统计2021年10月每个退货率不大于0.5的商品各项指标
统计2021年10月每个退货率不大于0.5的商品各项指标_牛客题霸_牛客网s mysql(ifnull): select product_id, format(ifnull(sum(if_click)/nullif(count(*),0),0),3) as ctr, format(ifnull(sum(if_cart)/nullif(sum(if_click),0),0),3) as c…...
【小波尺度谱】从分段离散小波变换计算小波尺度谱研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
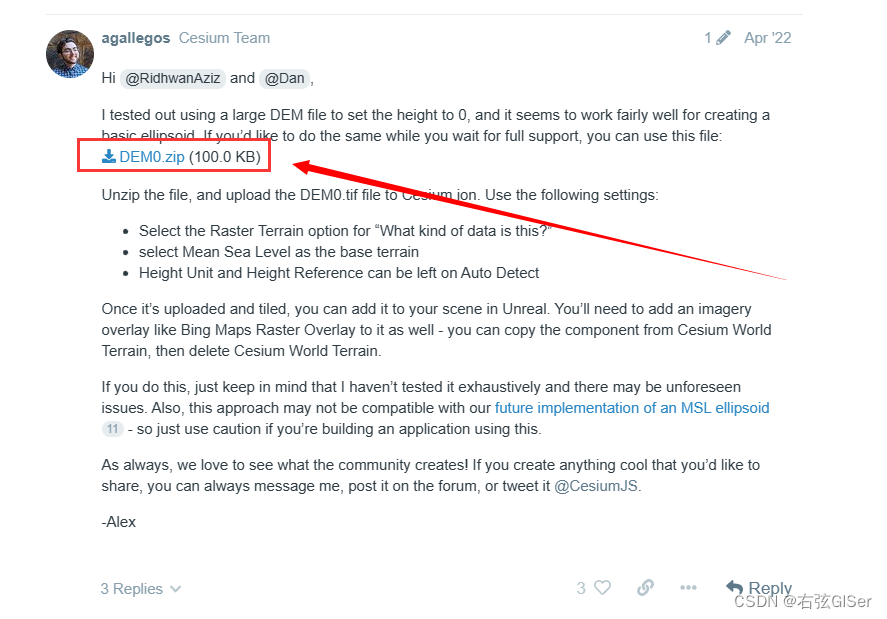
UE5、CesiumForUnreal加载无高度地形
文章目录 1.实现目标2.实现过程3.参考资料1.实现目标 在UE5中,CesiumForUnreal插件默认的地形都是带高度的,这里加载没有高度的地形,即大地高程为0,GIF动图如下: 2.实现过程 参考官方的教程,下载无高度的DEM,再切片加载到UE中。 (1)下载无高度地形DEM0。 在官方帖子…...

关于Spring中的@Configuration中的proxyBeanMethods属性
Configuration的proxyBeanMethods属性 在Configuration注解中,有两个属性: value配置Bean名称proxyBeanMethos,默认是true 这个proxyBeanMethods的默认属性是true。 直接说:当Configuration注解的proxyBeanMeathods属性是true…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
