AtCoder Beginner Contest 312(A~D)
A
//语法题也要更仔细嘞,要不然也会wa
#include <bits/stdc++.h>
// #pragma GCC optimize(3,"Ofast","inline")
// #pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
typedef pair<int, int> PII;
const int N = 1e6 + 10;void solve()
{string s;cin >> s;if(s=="ACE"||s=="BDF"||s=="CEG"||s=="DFA"||s=="EGB"||s=="FAC"||s=="GBD") cout << "Yes" << endl;else cout << "No" << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause"); return 0;
}
B
题意就是从一块大棋盘中抠出一块9*9指定的图案。数据范围不大,没有什么新奇的想法,直接遍历判断的。坐标的转换比较绕人//下次还是从1开始存吧
#include <bits/stdc++.h>
// #pragma GCC optimize(3,"Ofast","inline")
// #pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
typedef pair<int, int> PII;
const int N = 1e6 + 10;
int n, m;
char g[110][110];bool check(int x, int y)
{//左上角3*3的黑色for(int i = 0; i < 3; i ++ )for(int j = 0; j < 3; j ++ ){if(g[x+i][y+j] != '#') return false;}//右下角3*3的黑色for(int i = x + 8; i >= x + 6; i --)for(int j = y + 8; j >= y + 6; j -- )if(g[i][j] != '#') return false;//黑色周围的白色for(int i = 0; i < 4; i ++ ){if(g[x+3][y+i] != '.') return false;if(g[x+i][y + 3] !='.') return false; if(g[x+5][y+8-i] != '.') return false;if(g[x+8-i][y + 5] !='.') return false;}return true;
}void solve()
{ cin >> n >> m;for(int i = 0; i < n; i ++ ){for(int j = 0; j < m; j ++ ) cin >> g[i][j];}for(int i = 0; i < n - 8; i ++ )for(int j = 0; j < m - 8; j ++ ){if(check(i, j)){cout << i + 1<< ' ' << j + 1<< endl;} }}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause"); return 0;
}
C
思路:裸二分题,直接二分答案即可。
二分的时间复杂度是logn,check是n,nlogn能过。也可以给两个数组排序,对于每个mid在数组里二分查找坐标,但是排序的时间复杂度是nlogn,其实是一样的。
#include <bits/stdc++.h>
// #pragma GCC optimize(3,"Ofast","inline")
// #pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
typedef pair<int, int> PII;
const int N = 2e6 + 10;
int a[N], b[N];
int n, m;bool check(int mid)
{int cnt1 = 0, cnt2 = 0;for(int i = 1; i <= n; i ++ )if(a[i] <= mid) cnt1 ++;for(int i = 1; i <= m; i ++ )if(b[i] >= mid) cnt2 ++;return cnt2 <= cnt1;
}void solve()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> a[i];for (int j = 1; j <= m; j ++ ) cin >> b[j];int l = 0, r = 1e9 + 1, mid;//注意右边界不能是1e9,a和b的范围是1e9,但是实际出价的范围可以比1e9多while(l < r){mid = l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}cout << l << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause"); return 0;
}
D
dp题,f[i,j]表示前 i 个字符,剩余左括号数为 j 的方案数
#include <bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
#pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
const int N = 3010, mod = 998244353;
int f[N][N];void solve()
{ string s;cin >> s;s = '0' + s;f[0][0] = 1;for(int i = 1; i < s.size(); i ++ )for(int j = 0; j <= i; j ++ ){if(s[i] == '(') //如果第i位是左括号,那么情况与上一位 左括号数-1的情况相同f[i][j] = f[i - 1][j - 1];else if(s[i] == ')') //如果这位是右括号,情况与上一位 剩余左括号数+1情况相同f[i][j] = f[i - 1][j + 1];else //如果这一位是?,那么相当于可以是左括号也可以是右括号,情况为上面两种的和f[i][j] = (f[i - 1][j + 1] + f[i - 1][j - 1])%mod;}//遍历到最后一个字符串,并且左右括号恰好匹配(无剩余左括号)cout << f[s.size() - 1][0] << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause"); return 0;
}
相关文章:
)
AtCoder Beginner Contest 312(A~D)
A //语法题也要更仔细嘞,要不然也会wa #include <bits/stdc.h> // #pragma GCC optimize(3,"Ofast","inline") // #pragma GCC optimize(2) using namespace std; typedef long long LL; #define int LL typedef pair<int, int> …...

SQL中Partition的相关用法
使用Partition可以根据指定的列或表达式将数据分成多个分区。每个分区都是逻辑上独立的,可以单独进行查询、插入、更新和删除操作。Partition可以提高查询性能,因为它可以限制在特定分区上执行查询,而不是在整个表上执行。 在SQL中ÿ…...
微服务——Docker
docker与虚拟机的区别 首先要知道三个层次 硬件层:计算机硬件 内核层:与硬件交互,提供操作硬件的指令 应用层: 系统应用封装内核指令为函数,便于程序员调用。用户程序基于系统函数库实现功能。 docker在打包的时候直接把应用层的函数库也进行打包&a…...

测试|测试用例方法篇
测试|测试用例方法篇 文章目录 测试|测试用例方法篇1.测试用例的基本要素:测试环境,操作步骤,测试数据,预期结果…2.测试用例带来的好处3.测试用例的设计思路,设计方法,具体设计方法之间的关系**设计测试用…...

负载均衡的策略有哪些? 负载均衡的三种方式?
负载均衡的策略有哪些? 负载均衡的策略有如下: 1. 轮询(Round Robin):按照请求的顺序轮流分配到不同的服务器。 2. 权重(Weighted):给不同的服务器分配不同的权重,根据权重比例来…...
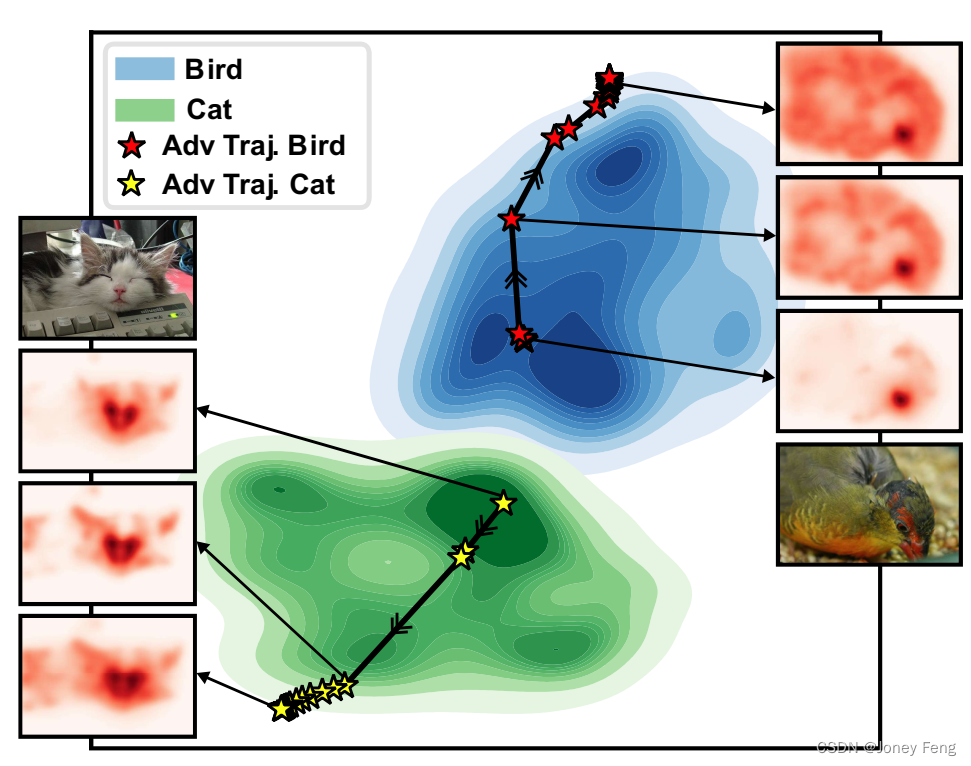
二十三章:抗对抗性操纵的弱监督和半监督语义分割的属性解释
0.摘要 弱监督语义分割从分类器中生成像素级定位,但往往会限制其关注目标对象的一个小的区域。AdvCAM是一种图像的属性图,通过增加分类分数来进行操作。这种操作以反对抗的方式实现,沿着像素梯度的相反方向扰动图像。它迫使最初被认为不具有区…...

curator实现的zookeeper可重入锁
Curator是一个Apache开源的ZooKeeper客户端库,它提供了许多高级特性和工具类,用于简化在分布式环境中使用ZooKeeper的开发。其中之一就是可重入锁。 Curator提供了InterProcessMutex类来实现可重入锁。以下是使用Curator实现ZooKeeper可重入锁的示例&am…...
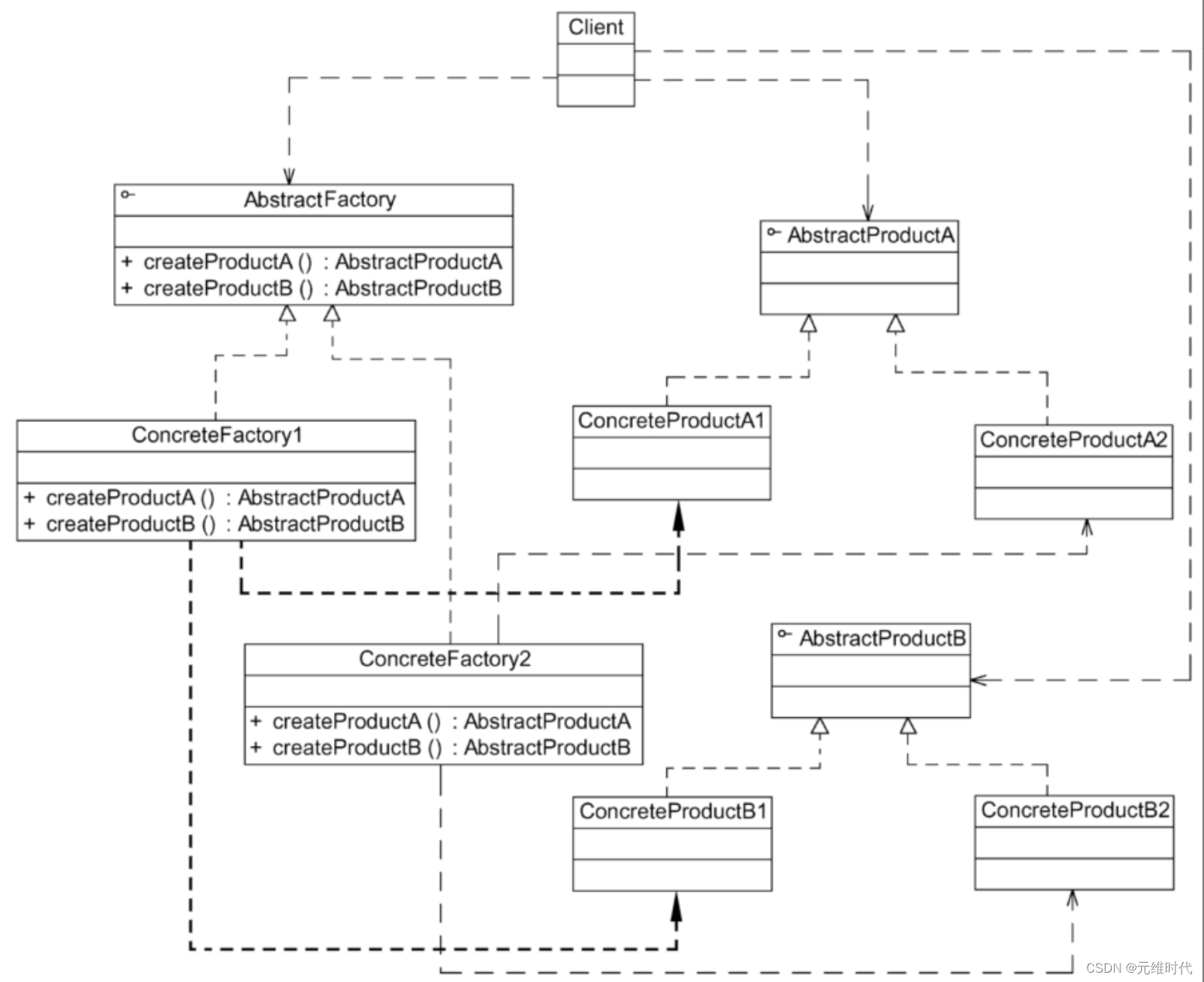
抽象工厂模式——产品族的创建
1、简介 1.1、简介 抽象工厂模式为创建一组对象提供了一种解决方案。与工厂方法模式相比,抽象工厂模式中的具体工厂不只是创建一种产品,它负责创建一族产品 1.2、定义 抽象工厂模式(Abstract Factory Pattern):提供…...

【C语言初阶篇】自定义类型结构体我不允许还有人不会!
🎬 鸽芷咕:个人主页 🔥 个人专栏:《C语言初阶篇》 《C语言进阶篇》 ⛺️生活的理想,就是为了理想的生活! 文章目录 📋 前言1 . 什么是结构体1.1 结构的定义1.2 结构的声明 2.结构体初始化2.1 用标签名定义和初始化2.2…...

重大更新|Sui主网即将上线流动性质押,助力资产再流通
Sui社区一直提议官方上线流动质押功能,现在通过SIP过程,已经升级该协议以实现这一功能。 Sui使用委托权益证明机制(DPoS)来选择和奖励负责运营网络的验证节点。为了保障网络安全,验证节点通过质押SUI token获得质押奖…...

day3 驱动开发 c语言编程
通过ioctl(内核应用层) 控制led灯三盏,风扇,蜂鸣器,小马达 头文件head.h #ifndef __LED_H__ #define __LED_H__typedef struct {volatile unsigned int TZCR; // 0x000volatile unsigned int res1[2]; // 0x…...
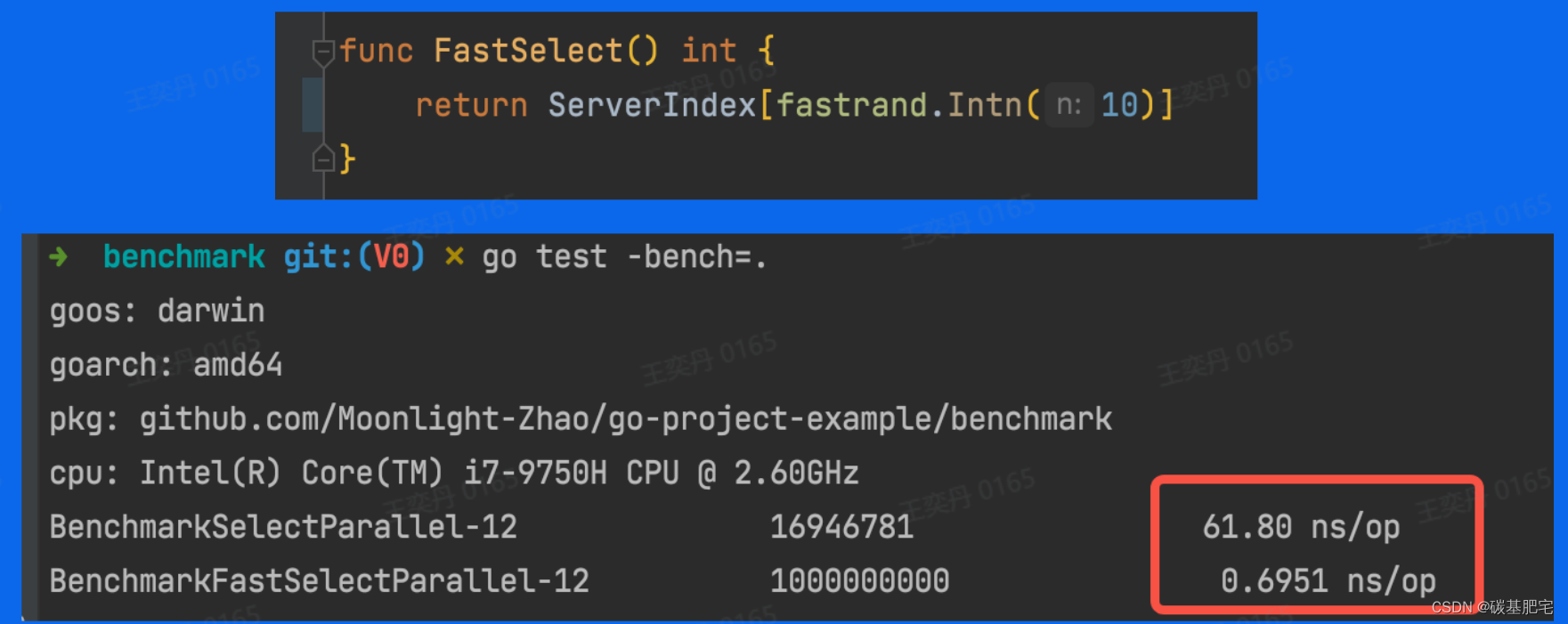
【字节跳动青训营】后端笔记整理-3 | Go语言工程实践之测试
**本文由博主本人整理自第六届字节跳动青训营(后端组),首发于稀土掘金:🔗Go语言工程实践之测试 | 青训营 目录 一、概述 1、回归测试 2、集成测试 3、单元测试 二、单元测试 1、流程 2、规则 3、单元测试的例…...

【Android】Recyclerview的缓存复用
介绍 RecyclerView是Android开发中常用的一个高度可定制的列表视图组件。它是在ListView和GridView的基础上进行了改进和增强,旨在提供更好的性能和更灵活的布局管理。 RecyclerView的主要特点如下: 灵活的布局管理器(LayoutManager&#…...
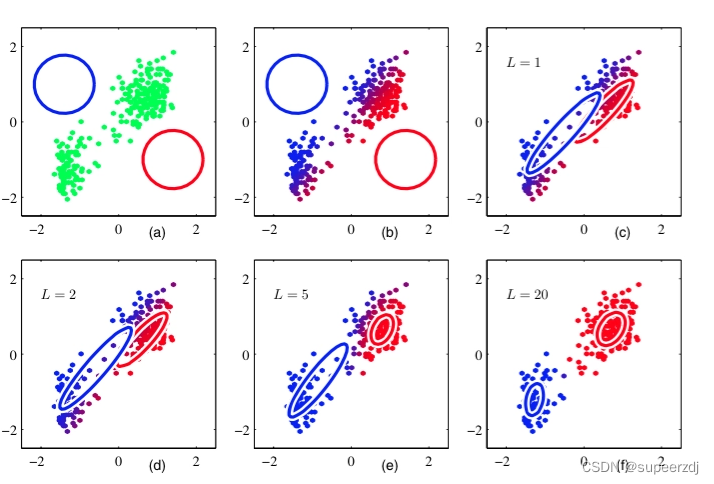
机器学习:混合高斯聚类GMM(求聚类标签)+PCA降维(3维降2维)习题
使用混合高斯模型 GMM,计算如下数据点的聚类过程: Datanp.array([1,2,6,7]) 均值初值为: μ1,μ21,5 权重初值为: w1,w20.5,0.5 方差: std1,std21,1 K2 10 次迭代后数据的聚类标签是多少? 采用python代码实现: from scipy import…...

libuv库学习笔记-processes
Processes libuv提供了相当多的子进程管理函数,并且是跨平台的,还允许使用stream,或者说pipe完成进程间通信。 在UNIX中有一个共识,就是进程只做一件事,并把它做好。因此,进程通常通过创建子进程来完成不…...

c++ 给无名形参提供默认值
如上图,若函数的形参不在函数体里使用,可以不提供形参名,而且可以给此形参提供默认值。也能编译通过。 在看vs2019上的源码时,也出现了这种写法。应用SFINAE(substitute false is not an error)原则&#x…...
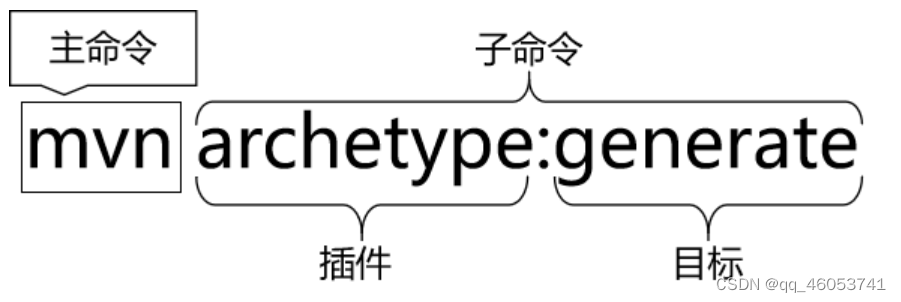
NO1.使用命令行创建Maven工程
①在工作空间目录下打开命令窗口 ②使用命令行生成Maven工程 mvn archetype:generate 运行 MVN 原型:生成命令,下面根据提示操作 选择一个数字或应用过滤器(格式:[groupId:]artifactId,区分大小写包含)&a…...

深度学习入门(一):神经网络基础
一、深度学习概念 1、定义 通过训练多层网络结构对位置数据进行分类或回归,深度学习解决特征工程问题。 2、深度学习应用 图像处理语言识别自然语言处理 在移动端不太好,计算量太大了,速度可能会慢 eg.医学应用、自动上色 3、例子 使用…...
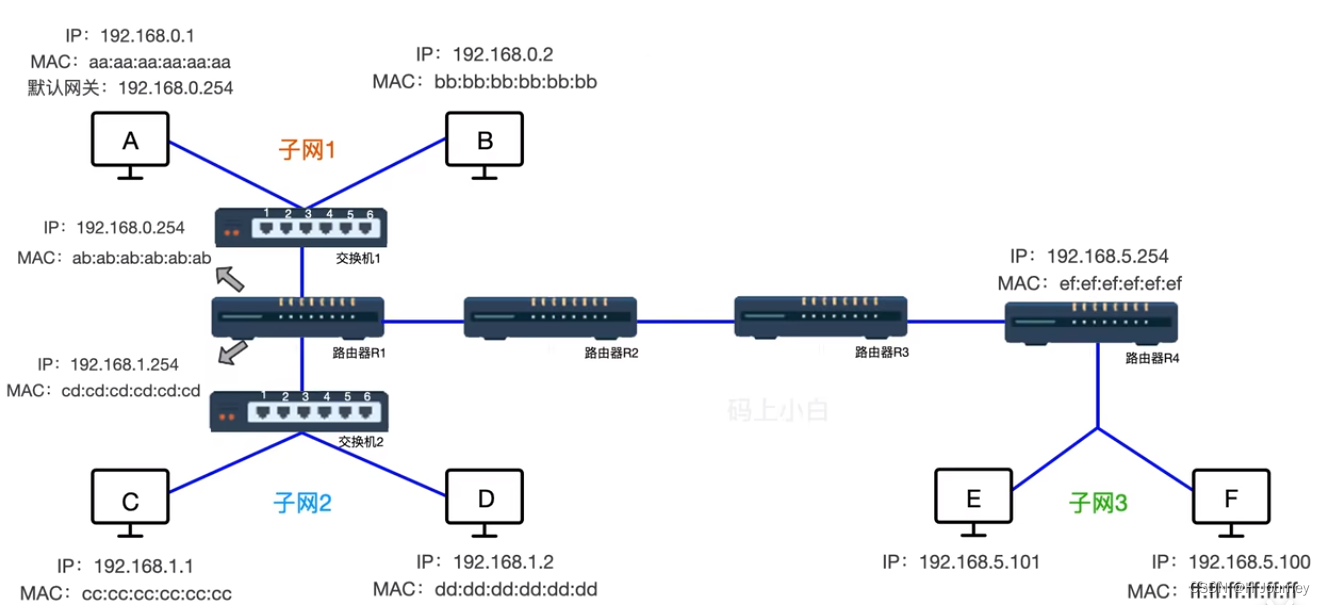
网络知识整理
网络知识整理 网络拓扑网关默认网关 数据传输拓扑结构层面协议层面 网络拓扑 网关 连接两个不同的网络的设备都可以叫网关设备,网关的作用就是实现两个网络之间进行通讯与控制。 网关设备可以是交换机(三层及以上才能跨网络) 、路由器、启用了路由协议的服务器、代…...

如何有效地使用ChatGPT写小说讲故事?
构思故事情节,虽有趣但耗时,容易陷入写作瓶颈。ChatGPT可提供灵感,帮你解决写作难题。要写出引人入胜的故事,关键在于抓住八个要素——主题、人物、视角、背景、情节、语气、冲突和解决办法。 直接给出故事模板,你可…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
