机器学习:混合高斯聚类GMM(求聚类标签)+PCA降维(3维降2维)习题
- 使用混合高斯模型 GMM,计算如下数据点的聚类过程:
Data=np.array([1,2,6,7])
均值初值为:
μ1,μ2=1,5
权重初值为:
w1,w2=0.5,0.5
方差:
std1,std2=1,1
K=2
10 次迭代后数据的聚类标签是多少?
采用python代码实现: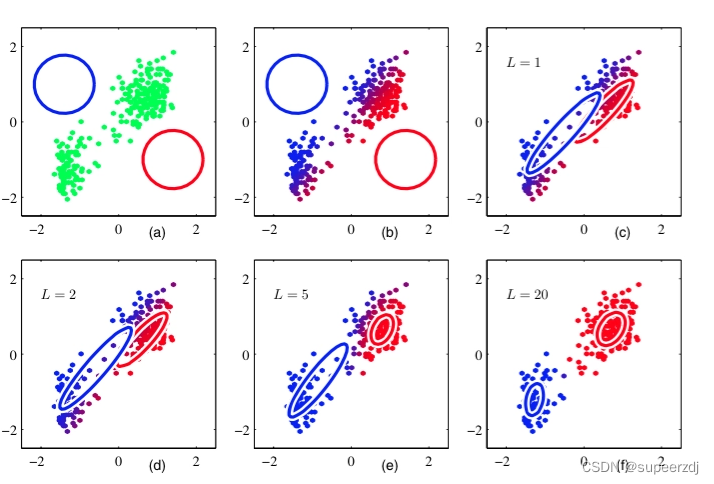
from scipy import stats
import numpy as np#初始化数据
Data = np.array([1,2,6,7])
w1 , w2 = 0.5, 0.5
mu1 , mu2 = 1, 5
std1 , std2 = 1, 1n = len(Data) # 样本长度
zij=np.zeros([n,2])
for t in range(10):# E-step 依据当前参数,计算每个数据点属于每个子分布的概率z1_up = w1 * stats.norm(mu1 ,std1).pdf(Data)z2_up = w2*stats.norm(mu2 , std2).pdf(Data)z_all = (w1*stats.norm(mu1 ,std1).pdf(Data)+w2*stats.norm(mu2 ,std2).pdf(Data))+0.001rz1 = z1_up/z_all # 为甲分布的概率rz2 = z2_up/z_all # 为乙分布的概率# M-step 依据 E-step 的结果,更新每个子分布的参数。mu1 = np.sum(rz1*Data)/np.sum(rz1)mu2 = np.sum(rz2*Data)/np.sum(rz2)std1 = np.sum(rz1*np.square(Data-mu1))/np.sum(rz1)std2 = np.sum(rz2*np.square(Data-mu2))/np.sum(rz2)w1 = np.sum(rz1)/nw2 = np.sum(rz2)/n
for i in range(n):zij[i][0] = rz1[i]/(rz1[i]+rz2[i])zij[i][1] = rz2[i]/(rz1[i]+rz2[i])labels = np.argmax(zij, axis=1)#输出每一行的最大值,0或1 axis表示返回每一行中最大值所在列的索引
print(labels)
聚类标签输出结果:[0 0 1 1]
也就是说,10 次迭代后数据的聚类标签是1,2归为0类6,7归为1类
附注:
如果 axis 为 None,那么 np.argmax 会将数组展平为一维,然后返回最大值的索引。例如:
>>> a = np.array([[1, 2], [3, 4]]) >>> np.argmax(a) 3如果 axis 为 0,那么 np.argmax 会沿着第一个维度(行)进行最大值的查找,返回每一列中最大值所在的行索引。例如:
>>> a = np.array([[1, 2], [3, 4]]) >>> np.argmax(a, axis=0) array([1, 1])如果 axis 为 1,那么 np.argmax 会沿着第二个维度(列)进行最大值的查找,返回每一行中最大值所在的列索引。例如:
>>> a = np.array([[1, 2], [3, 4]]) >>> np.argmax(a, axis=1) array([1, 1])在之前问题中,np.argmax([gamma1, gamma2], axis=0) 的意思是沿着第一个维度(gamma1 和 gamma2)进行最大值的查找,返回每个数据点属于哪个子分布的概率更大。
-
假设我们的数据集有 10 个 3 维数据, 需要用 PCA 降到 2 维特征。
array([[ 3.25, 1.85, -1.29],[ 3.06, 1.25, -0.18],[ 3.46, 2.68, 0.64],[ 0.3 , -0.1 , -0.79],[ 0.83, -0.21, -0.88],[ 1.82, 0.99, 0.16],[ 2.78, 1.75, 0.51],[ 2.08, 1.5 , -1.06],[ 2.62, 1.23, 0.04],[ 0.83, -0.69, -0.61]])给出求解过程
解:
- 对所有的样本进行中心化:
x(i)=x(i)−1m∑j=1mx(j)
得到:
X=np.array([[ 1.147 0.825 -0.944][ 0.957 0.225 0.166][ 1.357 1.655 0.986][-1.803 -1.125 -0.444][-1.273 -1.235 -0.534][-0.283 -0.035 0.506][ 0.677 0.725 0.856][-0.023 0.475 -0.714][ 0.517 0.205 0.386][-1.273 -1.715 -0.264]])
- 计算样本的协方差矩阵 XXT
covM2=np.array([[1.26344556 1.08743889 0.32030889],
[1.08743889 1.11076111 0.31611111],
[0.32030889 0.31611111 0.45449333]])
- 对矩阵 XXT 进行特征值分解
取出最大的 n′ 个特征值对应的特征向量 (w1,…,wn′), 将所有的特征向量标准化后,组成特征向量矩阵 W。
3.1求出特征值:
eigval=np.array([2.38219729 0.09637041 0.35013229])
3.2特征向量标准化:
eigvec=np.array([
[ 0.71144 0.67380165 -0.19961077],
[ 0.66498574 -0.73733944 -0.11884665],
[ 0.22725997 0.04818606 0.97264126]])
3.3取出特征值最大的2个特征值索引,也就是[2.38,0.35]对应的第1列和第3列:
indexes=[2 0]
3.4特征向量矩阵W:(对eigvec取了第3列和第1列)
W=np.array([
[-0.19961077 0.71144 ],
[-0.11884665 0.66498574],
[ 0.97264126 0.22725997]])
- 对样本集中的每一个样本 x(i) , 转化为新的样本 z(i)=WTx(i) ,得到输出样本集 D=(z(1),…z(m))
X:3×10 W:3×2 x⋅W=10×33×2 因为输入行列转置,结果是一致的
D=np.array([[-1.24517539 1.15010151][-0.05630956 0.86819503][ 0.49146125 2.29005381][ 0.06174799 -2.1317387 ][-0.1185103 -1.84827733][ 0.55280596 -0.10961848][ 0.6112806 1.15829407][-0.74632697 0.13724149][ 0.24787719 0.5918589 ][ 0.20114923 -2.10611029]])
代码:
import numpy as npX=np.array([[ 3.25, 1.85, -1.29],[ 3.06, 1.25, -0.18],[ 3.46, 2.68, 0.64],[ 0.3 , -0.1 , -0.79],[ 0.83, -0.21, -0.88],[ 1.82, 0.99, 0.16],[ 2.78, 1.75, 0.51],[ 2.08, 1.5 , -1.06],[ 2.62, 1.23, 0.04],[ 0.83, -0.69, -0.61]])def pca(X, d):# Centralization中心化means = np.mean(X, 0)X = X - meansprint(X)# Covariance Matrix 计算样本协方差矩阵M=len(X)X=np.mat(X) covM2=np.cov(X.T)# 求出特征值,特征值分解eigval , eigvec = np.linalg.eig(covM2)indexes = np.argsort(eigval)[-d:]W = eigvec[:, indexes]return X*W
print(pca(X, 2))
附注:
np.cov()是一个用于计算协方差矩阵的函数,它可以接受一个或两个数组作为参数,返回一个二维数组,表示协方差矩阵。
协方差矩阵是一个对称矩阵,它的对角线元素表示各个变量的方差,非对角线元素表示两个变量之间的协方差。协方差反映了两个变量的线性相关程度,如果协方差为正,说明两个变量正相关;如果协方差为负,说明两个变量负相关;如果协方差为零,说明两个变量无相关性。
np.cov()的用法如下:
np.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None)参数说明:
- m: 一个一维或二维的数组,表示多个变量和观测值。如果是一维数组,表示一个变量的观测值;如果是二维数组,每一行表示一个变量,每一列表示一个观测值。
- y: 可选参数,另一个一维或二维的数组,表示另一组变量和观测值,必须和m具有相同的形状。
- rowvar: 可选参数,布尔值,默认为True。如果为True,表示每一行代表一个变量;如果为False,表示每一列代表一个变量。
- bias: 可选参数,布尔值,默认为False。如果为False,表示计算无偏协方差(除以n-1);如果为True,表示计算有偏协方差(除以n)。
- ddof: 可选参数,整数,默认为None。如果不为None,则覆盖由bias隐含的默认值。ddof=0表示计算有偏协方差;ddof=1表示计算无偏协方差。
- fweights: 可选参数,一维数组或整数,默认为None。表示每次观测的频率权重。
- aweights: 可选参数,一维数组,默认为None。表示每个变量的可靠性权重。
返回值:
- 一个二维数组,表示协方差矩阵。
举例说明:
import numpy as np# 生成两组随机数据 x = np.random.randn(10) y = np.random.randn(10)# 计算x和y的协方差矩阵 cov_xy = np.cov(x,y) print(cov_xy) # 输出: [[ 0.8136679 -0.01594772][-0.01594772 0.84955963]]# 计算x和y的相关系数矩阵 corr_xy = np.corrcoef(x,y) print(corr_xy) # 输出: [[ 1. -0.01904402][-0.01904402 1. ]]
相关文章:

机器学习:混合高斯聚类GMM(求聚类标签)+PCA降维(3维降2维)习题
使用混合高斯模型 GMM,计算如下数据点的聚类过程: Datanp.array([1,2,6,7]) 均值初值为: μ1,μ21,5 权重初值为: w1,w20.5,0.5 方差: std1,std21,1 K2 10 次迭代后数据的聚类标签是多少? 采用python代码实现: from scipy import…...

libuv库学习笔记-processes
Processes libuv提供了相当多的子进程管理函数,并且是跨平台的,还允许使用stream,或者说pipe完成进程间通信。 在UNIX中有一个共识,就是进程只做一件事,并把它做好。因此,进程通常通过创建子进程来完成不…...

c++ 给无名形参提供默认值
如上图,若函数的形参不在函数体里使用,可以不提供形参名,而且可以给此形参提供默认值。也能编译通过。 在看vs2019上的源码时,也出现了这种写法。应用SFINAE(substitute false is not an error)原则&#x…...
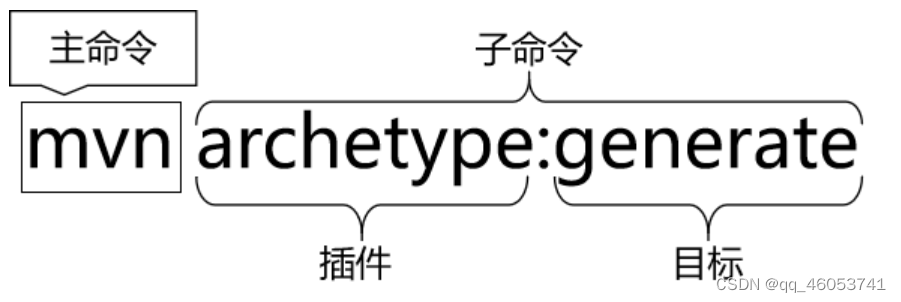
NO1.使用命令行创建Maven工程
①在工作空间目录下打开命令窗口 ②使用命令行生成Maven工程 mvn archetype:generate 运行 MVN 原型:生成命令,下面根据提示操作 选择一个数字或应用过滤器(格式:[groupId:]artifactId,区分大小写包含)&a…...

深度学习入门(一):神经网络基础
一、深度学习概念 1、定义 通过训练多层网络结构对位置数据进行分类或回归,深度学习解决特征工程问题。 2、深度学习应用 图像处理语言识别自然语言处理 在移动端不太好,计算量太大了,速度可能会慢 eg.医学应用、自动上色 3、例子 使用…...
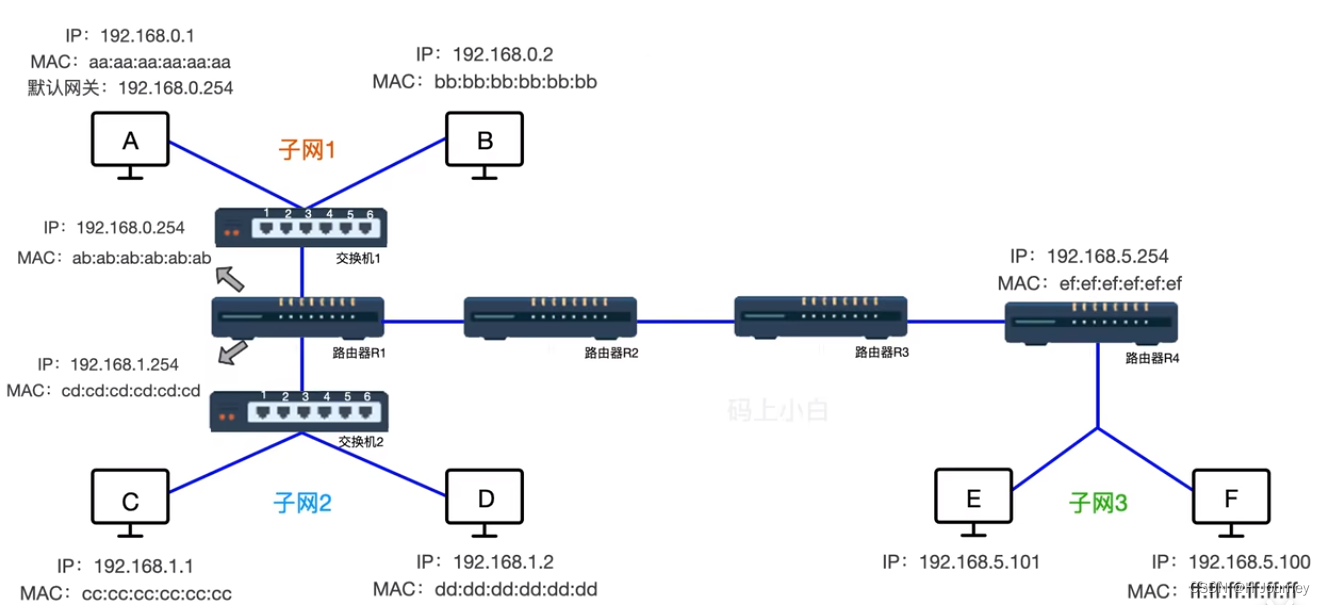
网络知识整理
网络知识整理 网络拓扑网关默认网关 数据传输拓扑结构层面协议层面 网络拓扑 网关 连接两个不同的网络的设备都可以叫网关设备,网关的作用就是实现两个网络之间进行通讯与控制。 网关设备可以是交换机(三层及以上才能跨网络) 、路由器、启用了路由协议的服务器、代…...

如何有效地使用ChatGPT写小说讲故事?
构思故事情节,虽有趣但耗时,容易陷入写作瓶颈。ChatGPT可提供灵感,帮你解决写作难题。要写出引人入胜的故事,关键在于抓住八个要素——主题、人物、视角、背景、情节、语气、冲突和解决办法。 直接给出故事模板,你可…...

原生求生记:揭秘UniApp的原生能力限制
文章目录 1. 样式适配问题2. 性能问题3. 原生能力限制4. 插件兼容性问题5. 第三方组件库兼容性问题6. 全局变量污染7. 调试和定位问题8. 版本兼容性问题9. 前端生态限制10. 文档和支持附录:「简历必备」前后端实战项目(推荐:⭐️⭐️⭐️⭐️…...
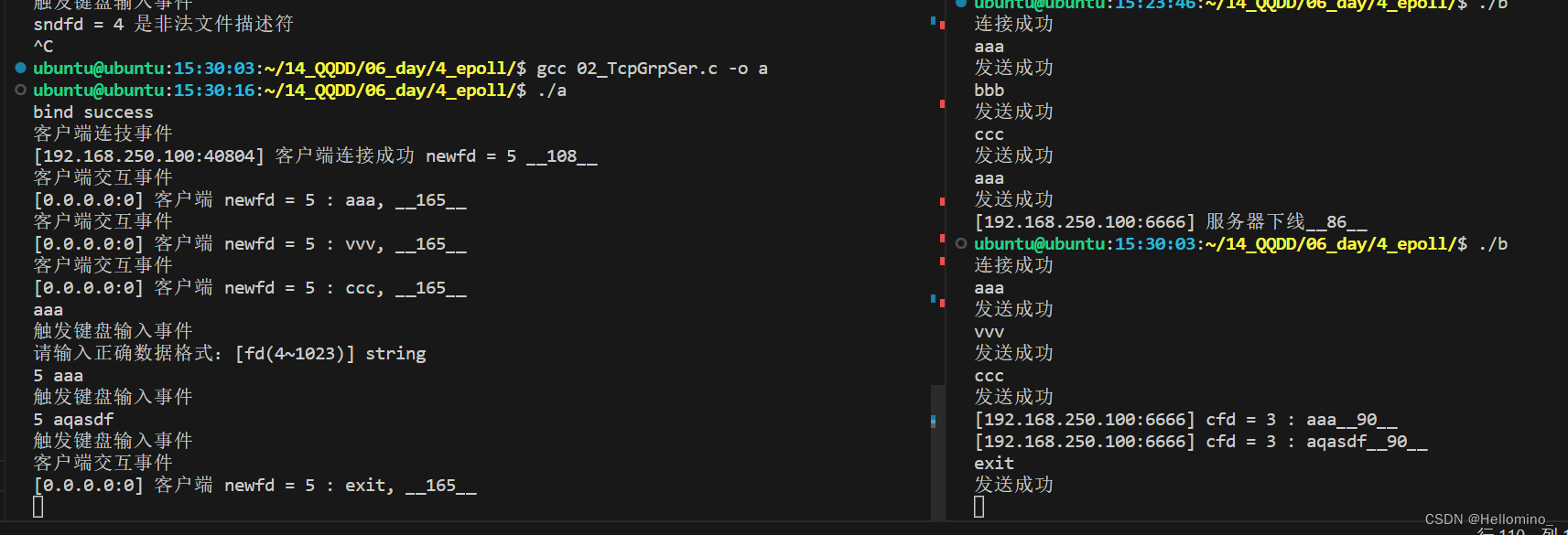
网络编程 IO多路复用 [epoll版] (TCP网络聊天室)
//head.h 头文件 //TcpGrpSer.c 服务器端 //TcpGrpUsr.c 客户端 通过IO多路复用实现服务器在单进程单线程下可以与多个客户端交互 API epoll函数 #include<sys/epoll.h> int epoll_create(int size); 功能:创建一个epoll句柄//创建红黑树根…...
【go-zero】浅析 01
“github.com/google/uuid” uuid.New().String() go-zero 文档 https://www.w3cschool.cn/gozero/ go-zero 官网 https://go-zero.dev/ 快速开始: $ mkdir go-zero-demo $ cd go-zero-demo $ go mod init go-zero-demo $ goctl api new greet $ go mod tidy Done…...
音视频——视频流H264编码格式
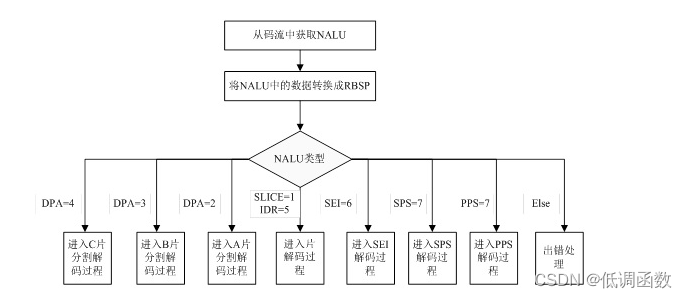
1 H264介绍 我们了解了什么是宏快,宏快作为压缩视频的最小的一部分,需要被组织,然后在网络之间做相互传输。 H264更深层次 —》宏块 太浅了 如果单纯的用宏快来发送数据是杂乱无章的,就好像在没有集装箱 出现之前,…...
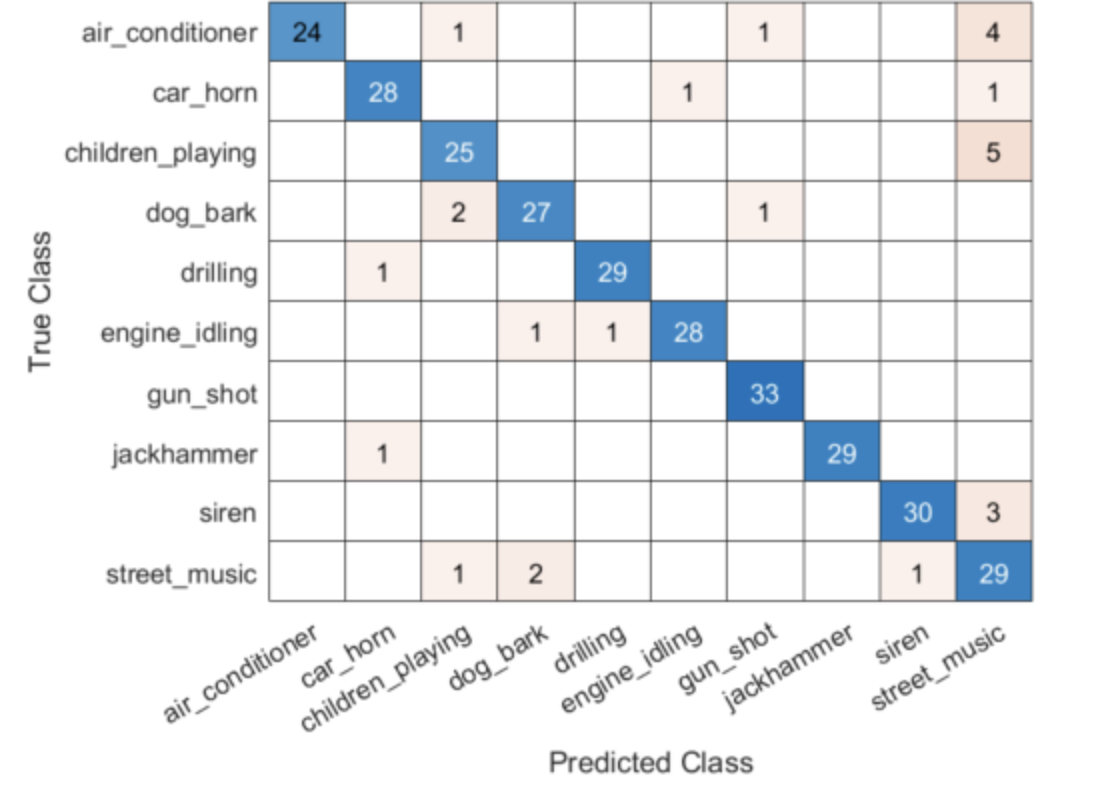
【使用深度学习的城市声音分类】使用从提取音频特征(频谱图)中提取的深度学习进行声音分类研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

机器学习完整路径
一个机器学习项目从开始到结束大致分为 5 步,分别是定义问题、收集数据和预处理、选择算法和确定模型、训练拟合模型、评估并优化模型性能。是一个循环迭代的过程,优秀的模型都是一次次迭代的产物。 定义问题 要剖析业务场景,设定清晰的目标…...
CK-00靶机详解
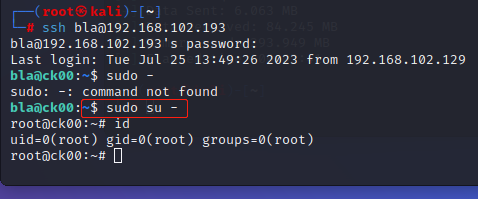
CK-00靶机详解 靶场下载地址:https://download.vulnhub.com/ck/CK-00.zip 这个靶场扫描到ip打开后发现主页面css是有问题的,一般这种情况就是没有配置域名解析。 我们网站主页右击查看源代码,发现一个域名。 把域名添加到我们hosts文件中。…...
17-C++ 数据结构 - 栈
📖 1.1 什么是栈 栈是一种线性数据结构,具有后进先出(Last-In-First-Out,LIFO)的特点。可以类比为装满盘子的餐桌,每次放盘子都放在最上面,取盘子时也从最上面取,因此最后放进去的盘…...
Redis如何实现排行榜?
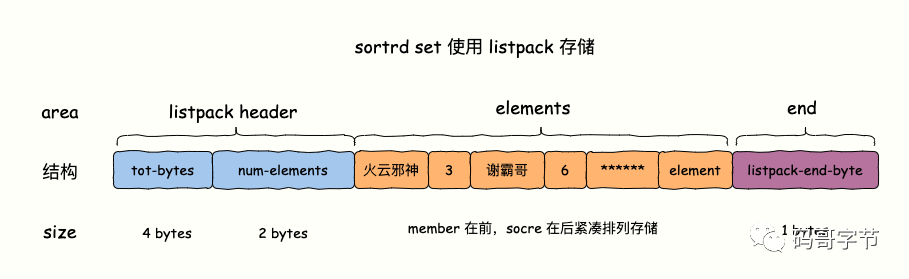
今天给大家简单聊聊 Redis Sorted Set 数据类型底层的实现原理和游戏排行榜实战。特别简单,一点也不深入,也就 7 张图,粉丝可放心食用,哈哈哈哈哈~~~~。 1. 是什么 Sorted Sets 与 Sets 类似,是一种集合类型ÿ…...

Pycharm debug程序,跳转至指定循环条件/循环次数
在断点出右键,然后设置条件 示例 for i in range(1,100):a i 1b i 2print(a, b, i) 注意: 1、你应该debug断点在循环后的位置而不是循环上的位置,然后你就可以设置你的条件进入到指定的循环上了 2、设置条件,要使用等于符号…...

react实现markdown
参考:https://blog.csdn.net/Jack_lzx/article/details/118495763 参考:https://blog.csdn.net/m0_48474585/article/details/119742984 0. 示例 用react实现markdown编辑器 1.基本布局及样式 <><div classNametf_editor_header>头部&…...
HTTP请求走私漏洞简单分析
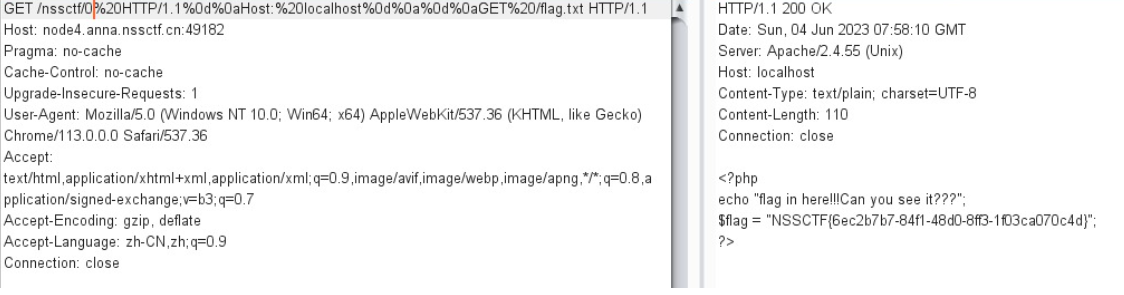
文章目录 HTTP请求走私漏洞的产生HTTP请求走私漏洞的分类HTTP请求走私攻击的危害确认HTTP请求走私漏洞通过时间延迟技术确认CL漏洞通过时间延迟技术寻找TE.CL漏洞 使用差异响应内容确认漏洞通过差异响应确认CL.TE漏洞通过差异响应确认TE.CL漏洞 请求走私漏洞的利用通过请求漏洞…...
BI-SQL丨两表差异比较
BOSS:哎,白茶,我们最近新上了一个系统,后续有一些数据要进行源切换,这个能整么? 白茶:没问题,可以整! BOSS:哦,对了,差点忘记告诉你了…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
