17-C++ 数据结构 - 栈
📖 1.1 什么是栈
栈是一种线性数据结构,具有后进先出(Last-In-First-Out,LIFO)的特点。可以类比为装满盘子的餐桌,每次放盘子都放在最上面,取盘子时也从最上面取,因此最后放进去的盘子最先取出。栈的典型应用场景有函数调用、括号匹配、表达式求值等。
元素从固定一侧开口进入和离开栈的操作,分别称为入栈和出栈。
栈中元素由深到浅存储,我们将栈最深的存储位置称为栈底,当前栈中最外围元素所在的位置则称为栈顶。
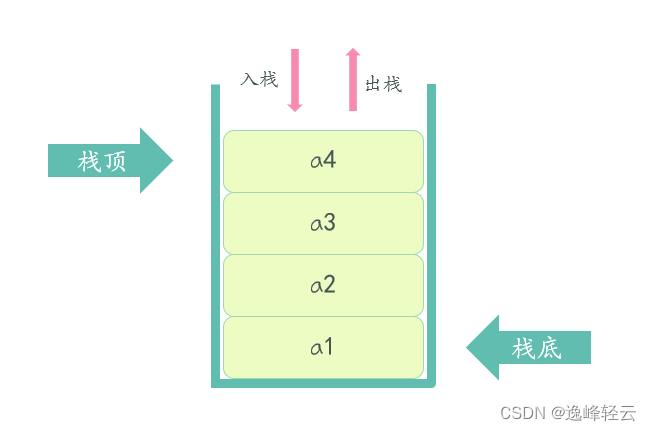
栈底通常固定不变,而栈顶则由当前栈中最外侧元素位置(栈中元素数量)确定。
由栈的特点可知栈的插入和删除(入栈和出栈)操作都是在栈顶这一端进行的。
栈顶(Top):线性表允许进行插入删除的那一端。
栈底(Bottom):固定的,不允许进行插入和删除的另一端。
空栈:不含任何元素的空表。
栈又称为后进先出(Last In First Out)的线性表,简称LIFO结构
栈的常见基本操作
InitStack(&S):初始化一个空栈S 。
StackEmpty(S):判断一个栈是否为空,若栈为空则返回true,否则返回false。
Push(&S, x):进栈(栈的插入操作),若栈S未满,则将x加入使之成为新栈顶。
Pop(&S, &x):出栈(栈的删除操作),若栈S非空,则弹出栈顶元素,并用x返回。
GetTop(S, &x):读栈顶元素,若栈S非空,则用x返回栈顶元素。
DestroyStack(&S):栈销毁,并释放S占用的存储空间(“&”表示引用调用)。
💻 1.2 栈的实现(数组模拟)
栈的实现可以使用数组来模拟。我们可以定义一个固定大小的数组和一个指向栈顶的指针。栈顶指针初始化为 -1,表示栈为空。每次入栈操作时,将元素放入数组并将栈顶指针加一;出栈操作时,将栈顶指针减一。
#include <iostream>
using namespace std;const int MAX_SIZE = 100; // 栈的最大容量
int stack[MAX_SIZE]; // 栈的数组
int top = -1; // 栈顶指针// 入栈操作
void push(int x) {if (top >= MAX_SIZE - 1) {cout << "栈已满,无法入栈!" << endl;return;}stack[++top] = x;
}// 出栈操作
void pop() {if (top == -1) {cout << "栈为空,无法出栈!" << endl;return;}top--;
}// 获取栈顶元素
int peek() {if (top == -1) {cout << "栈为空,无栈顶元素!" << endl;return -1;}return stack[top];
}// 判断栈是否为空
bool isEmpty() {return top == -1;
}// 获取栈的大小
int size() {return top + 1;
}int main() {push(1);push(2);push(3);cout << "当前栈顶元素:" << peek() << endl;cout << "栈的大小:" << size() << endl;pop();cout << "当前栈顶元素:" << peek() << endl;cout << "栈是否为空:" << (isEmpty() ? "是" : "否") << endl;return 0;
}
运行结果:
当前栈顶元素:3
栈的大小:3
当前栈顶元素:2
栈是否为空:否
📚 1.3 栈的实现(STL 方法)
在 C++ 中,我们也可以使用标准模板库(STL)提供的 stack 容器来实现栈。使用 stack 容器非常方便,不需要手动处理数组和指针。
#include <iostream>
#include <stack>
using namespace std;int main() {stack<int> st;st.push(1);st.push(2);st.push(3);cout << "当前栈顶元素:" << st.top() << endl;cout << "栈的大小:" << st.size() << endl;st.pop();cout << "当前栈顶元素:" << st.top() << endl;cout << "栈是否为空:" << (st.empty() ? "是" : "否") << endl;return 0;
}
运行结果:
当前栈顶元素:3
栈的大小:3
当前栈顶元素:2
栈是否为空:否
使用 stack 容器,我们可以更方便地实现栈的入栈、出栈、获取栈顶元素等操作,而无需自己处理底层的数据结构。
🚂 1.4 出入栈顺序(火车调度案例)
火车调度是一个经典的栈的应用场景。给定 n 辆火车的进站顺序,请输出所有可能的出站顺序。
我们使用递归来生成所有可能的出站顺序。对于每一辆火车,它可以先进站再出站,也可以直接从进站过程中出站。我们不断尝试所有可能的出站顺序,直到所有火车都出站。
#include <iostream>
#include <vector>
using namespace std;void dfs(vector<int>& in, vector<int>& out, vector<int>& path) {if (in.empty() && out.empty()) {for (int num : path) {cout << num << " ";}cout << endl;return;}if (!in.empty()) {int num = in.back();in.pop_back();path.push_back(num);dfs(in, out, path);path.pop_back();in.push_back(num);}if (!out.empty()) {int num = out.back();out.pop_back();path.push_back(num);dfs(in, out, path);path.pop_back();out.push_back(num);}
}int main() {vector<int> in = {1, 2, 3};vector<int> out;vector<int> path;dfs(in, out, path);return 0;
}
运行结果:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
🧩 1.5 栈的应用
有效的括号
题目描述
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
提示:
1 <= s.length <= 104s仅由括号'()[]{}'组成
力扣官方题解https://leetcode.cn/problems/valid-parentheses/solutions/373578/you-xiao-de-gua-hao-by-leetcode-solution/
我们遍历给定的字符串 s。当我们遇到一个左括号时,我们会期望在后续的遍历中,有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合,因此我们可以将这个左括号放入栈顶。
当我们遇到一个右括号时,我们需要将一个相同类型的左括号闭合。此时,我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型,或者栈中并没有左括号,那么字符串 s 无效,返回False。为了快速判断括号的类型,我们可以使用哈希表存储每一种括号。哈希表的键为右括号,值为相同类型的左括号。
在遍历结束后,如果栈中没有左括号,说明我们将字符串 s 中的所有左括号闭合,返回 True,否则返回 False。
注意到有效字符串的长度一定为偶数,因此如果字符串的长度为奇数,我们可以直接返回 False,省去后续的遍历判断过程。
栈在括号匹配中有着重要的应用。给定一个只包含 (、)、[、]、{ 和 } 的字符串,判断括号是否匹配。
使用栈可以轻松解决这个问题。遍历字符串中的每个字符,如果是左括号,将其入栈;如果是右括号,判断与栈顶元素是否匹配,若匹配则出
栈,否则返回 false。最后检查栈是否为空,为空则括号匹配。
#include <iostream>
#include <stack>
#include <unordered_map>
using namespace std;bool isValid(string s) {stack<char> st;unordered_map<char, char> mapping = {{')', '('}, {']', '['}, {'}', '{'}};for (char c : s) {if (c == '(' || c == '[' || c == '{') {st.push(c);} else if (c == ')' || c == ']' || c == '}') {if (st.empty() || st.top() != mapping[c]) {return false;}st.pop();}}return st.empty();
}int main() {cout << isValid("()") << endl; // 输出:1 (true)cout << isValid("()[]{}") << endl; // 输出:1 (true)cout << isValid("(]") << endl; // 输出:0 (false)return 0;
}
📝 总结
栈是一种非常重要的数据结构,在计算机算法中有着广泛的应用。通过模拟入栈和出栈操作,我们可以解决很多实际问题,比如火车调度、括号匹配等。同时,C++ 中也提供了标准模板库(STL)中的 stack 容器,方便我们使用栈来解决问题。熟练掌握栈的使用将会对你的编程技能有很大的提升。
⭐️希望本篇文章对你有所帮助。
⭐️如果你有任何问题或疑惑,请随时向提问。
⭐️感谢阅读!
相关文章:

17-C++ 数据结构 - 栈
📖 1.1 什么是栈 栈是一种线性数据结构,具有后进先出(Last-In-First-Out,LIFO)的特点。可以类比为装满盘子的餐桌,每次放盘子都放在最上面,取盘子时也从最上面取,因此最后放进去的盘…...
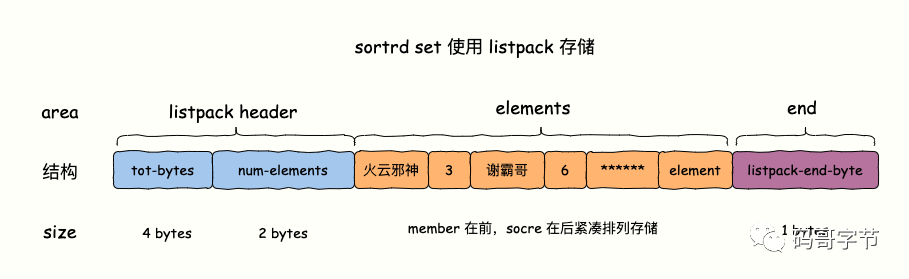
Redis如何实现排行榜?
今天给大家简单聊聊 Redis Sorted Set 数据类型底层的实现原理和游戏排行榜实战。特别简单,一点也不深入,也就 7 张图,粉丝可放心食用,哈哈哈哈哈~~~~。 1. 是什么 Sorted Sets 与 Sets 类似,是一种集合类型ÿ…...

Pycharm debug程序,跳转至指定循环条件/循环次数
在断点出右键,然后设置条件 示例 for i in range(1,100):a i 1b i 2print(a, b, i) 注意: 1、你应该debug断点在循环后的位置而不是循环上的位置,然后你就可以设置你的条件进入到指定的循环上了 2、设置条件,要使用等于符号…...

react实现markdown
参考:https://blog.csdn.net/Jack_lzx/article/details/118495763 参考:https://blog.csdn.net/m0_48474585/article/details/119742984 0. 示例 用react实现markdown编辑器 1.基本布局及样式 <><div classNametf_editor_header>头部&…...
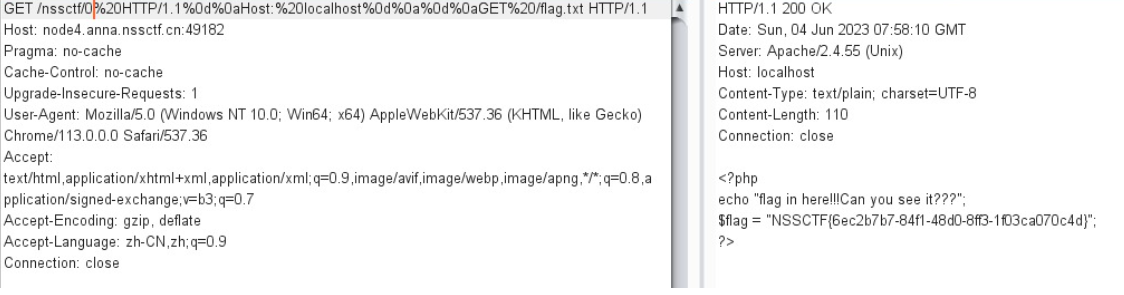
HTTP请求走私漏洞简单分析
文章目录 HTTP请求走私漏洞的产生HTTP请求走私漏洞的分类HTTP请求走私攻击的危害确认HTTP请求走私漏洞通过时间延迟技术确认CL漏洞通过时间延迟技术寻找TE.CL漏洞 使用差异响应内容确认漏洞通过差异响应确认CL.TE漏洞通过差异响应确认TE.CL漏洞 请求走私漏洞的利用通过请求漏洞…...
BI-SQL丨两表差异比较
BOSS:哎,白茶,我们最近新上了一个系统,后续有一些数据要进行源切换,这个能整么? 白茶:没问题,可以整! BOSS:哦,对了,差点忘记告诉你了…...

ZooKeeper 选举的过半机制防止脑裂
结论: Zookeeper采用过半选举机制,防止了脑裂。 原因: 如果有5台节点,leader联系不上了,其他4个节点由于超过半数,所以又选出了一个leader,当失联的leader恢复网络时,发现集群中已…...
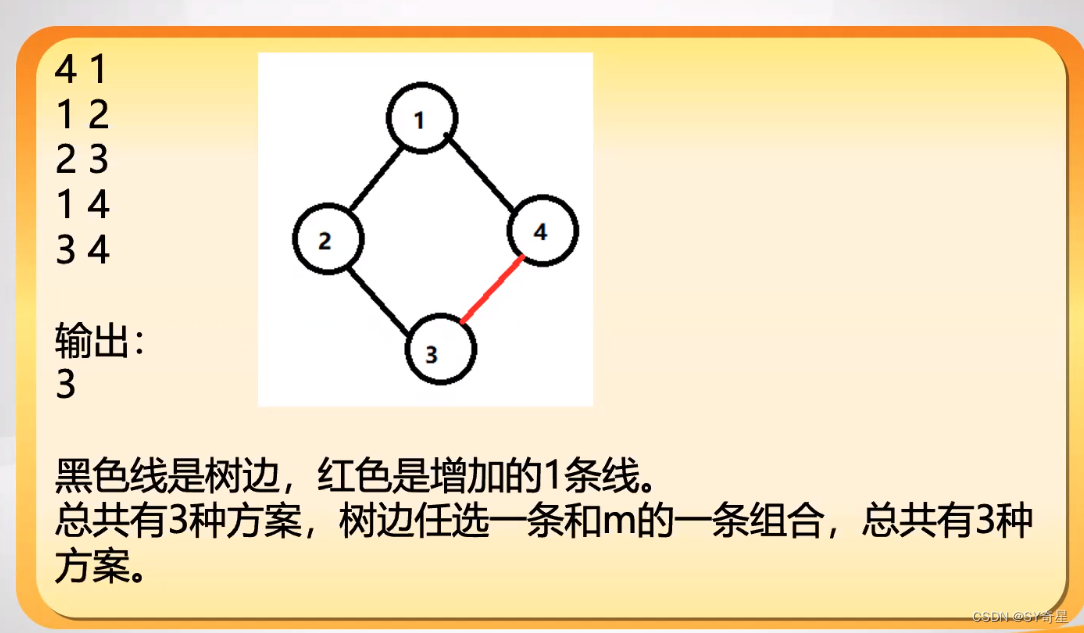
【图论】树上差分(边差分)
一.简介 其实点差分和边差分区别不大。 点差分中,d数组存储的是树上的节点 边差分中,d数组存储的是当前节点到父节点的那条边的差分值。 指定注意的是:边差分中因为根连的父节点是虚点,所以遍历结果时应当忽略! 二…...
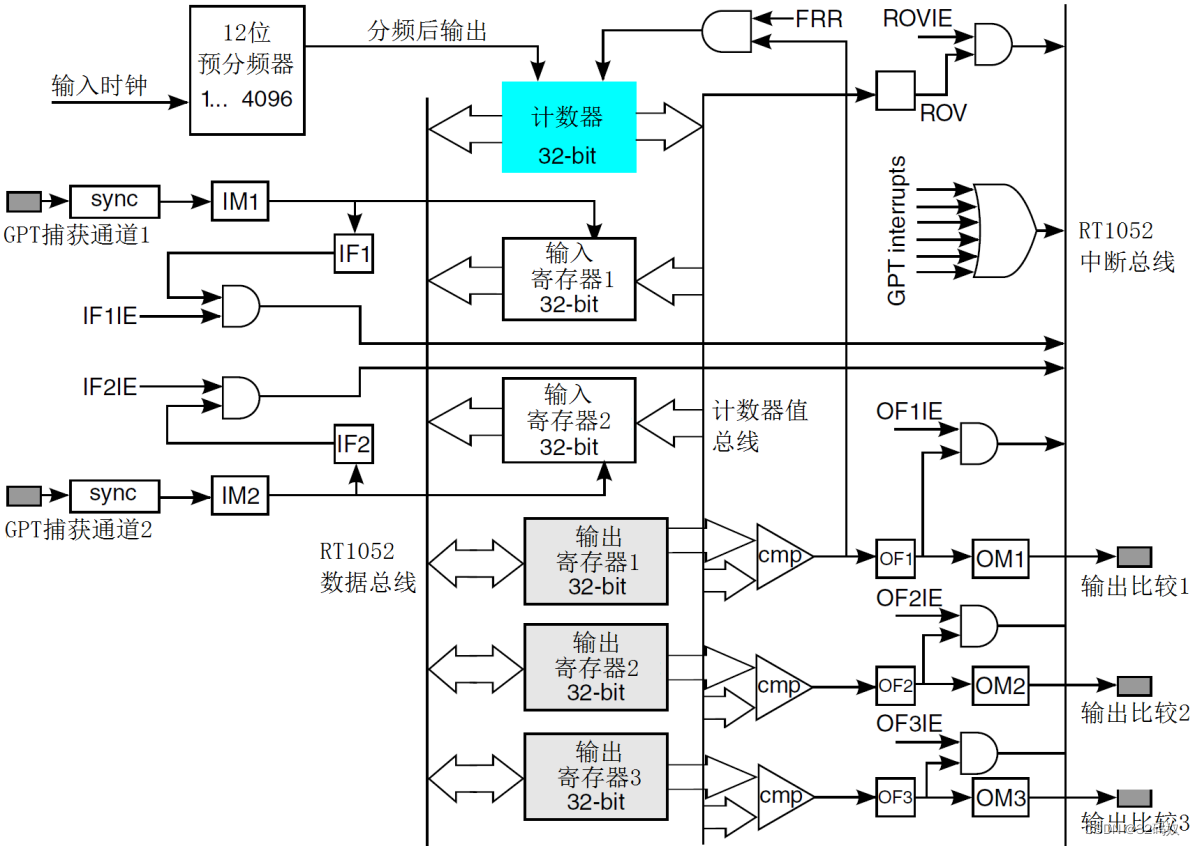
RT1052的定时器
文章目录 1 通用定时器1.1 定时器框图1.2 实现周期性中断 2 相关寄存器3 定时器配置3.1 时钟使能3.2 初始化GPT1定时器3.2.1 base3.2.2 initConfig3.2.2.1 clockSorce3.2.2.2 divider3.2.2.3 enablexxxxx 3.3 设置 GPT1 比较值3.3.1 base3.3.2 channel3.3.3 value 3.4 设置 GPT…...
opencv python 训练自己的分类器
源码下载 一、分类器制作 1.样本准备 收集好你所需的正样本,和负样本,分别保存在不同文件夹 在pycharm新建项目,项目结构如下:has_mask文件夹放置正样本,no_mask文件夹放置负样本 安装opencv,把opencv包…...
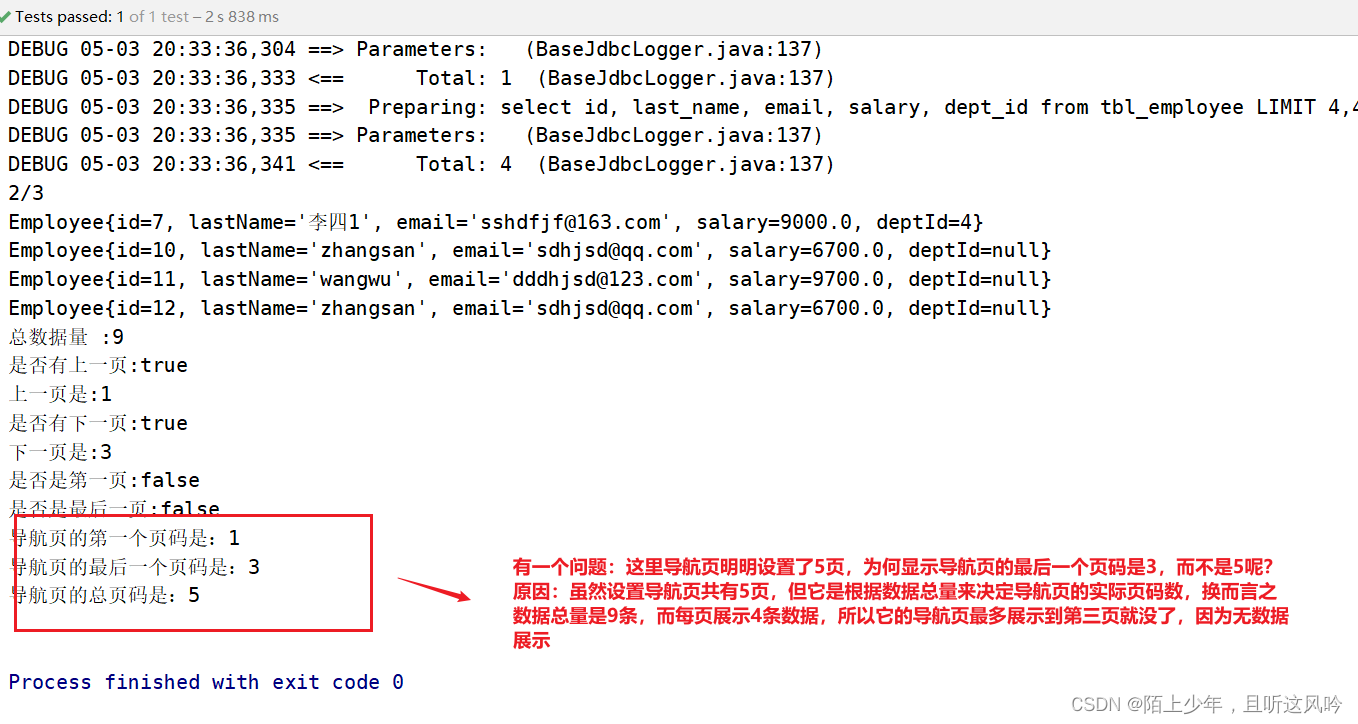
详解Mybatis之分页插件【PageHelper】
编译软件:IntelliJ IDEA 2019.2.4 x64 操作系统:win10 x64 位 家庭版 Maven版本:apache-maven-3.6.3 Mybatis版本:3.5.6 文章目录 一. 什么是分页?二. 为什么使用分页?三. 如何设计一个Page类(分…...
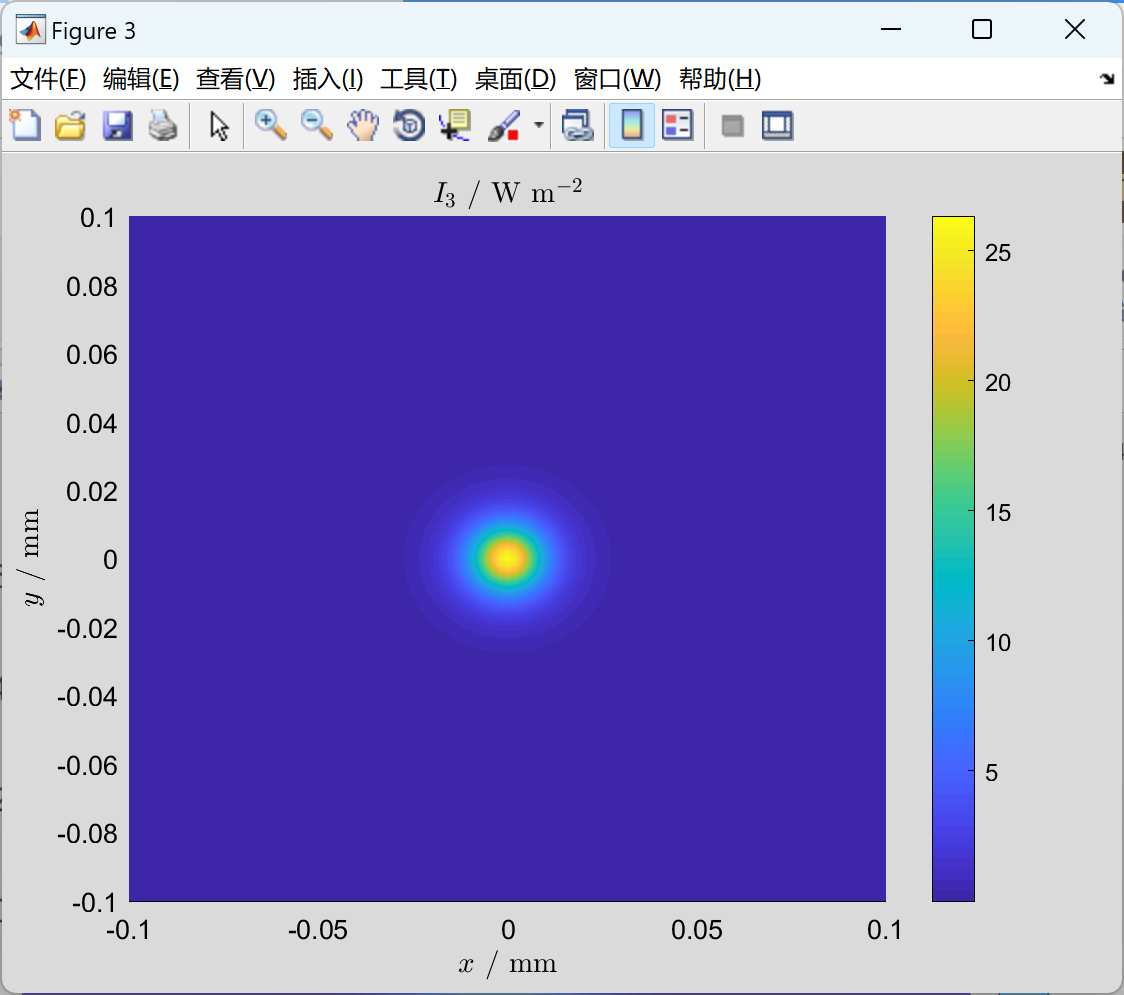
【基于矢量射线的衍射积分 (VRBDI)】基于矢量射线的衍射积分 (VRBDI) 和仿真工具(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

基于jackson对bean的序列号和反序列化
通过观察控制台输出的SQL发现页面传递过来的员工id的值和数据库中的id值不一致,这是怎么回事呢? 分页查询时服务端响应给页面的数据中id的值为19位数字,类型为long 页面中js处理long型数字只能精确到前16位,所以最终通过ajax请求提交给服务…...

排队理论简介
排队理论简介 1. 理论背景2. 研究的数学方法3. 拒绝型排队系统与等候型排队系统4. 拒绝型排队系统 本文参考文献为Вентцель Е. С.的《Исследование операций》。 1. 理论背景 排队理论又称大众服务理论,顾名思义指的是在有限的服务条…...
-算法分析)
极速查找(3)-算法分析
篇前小言 本篇文章是对查找(2)的续讲二叉排序树 二叉排序树(Binary Search Tree,BST),又称为二叉查找树,是一种特殊的二叉树。性质: 左子树的节点值小于根节点的值,右…...

http 常见的响应状态码 ?
100——客户必须继续发出请求101——客户要求服务器根据请求转换HTTP协议版本200——交易成功201——提示知道新文件的URL202——接受和处理、但处理未完成203——返回信息不确定或不完整204——请求收到,但返回信息为空205——服务器完成了请求,用户代理…...
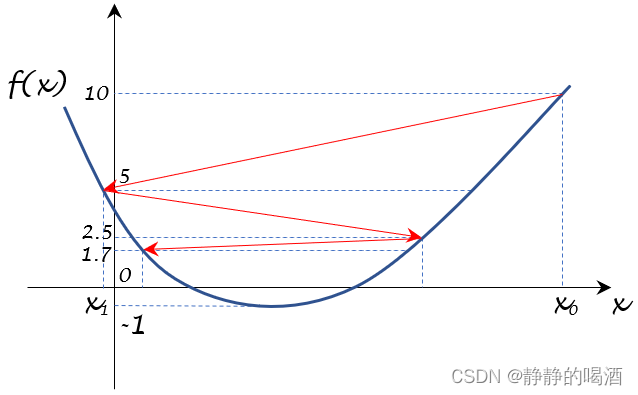
机器学习笔记之优化算法(四)线搜索方法(步长角度;非精确搜索)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索] 引言回顾:精确搜索步长及其弊端非精确搜索近似求解最优步长的条件反例论述 引言 上一节介绍了从精确搜索的步长角度观察了线搜索方法,本节将从非精确搜索的步长角度重新观察线搜…...
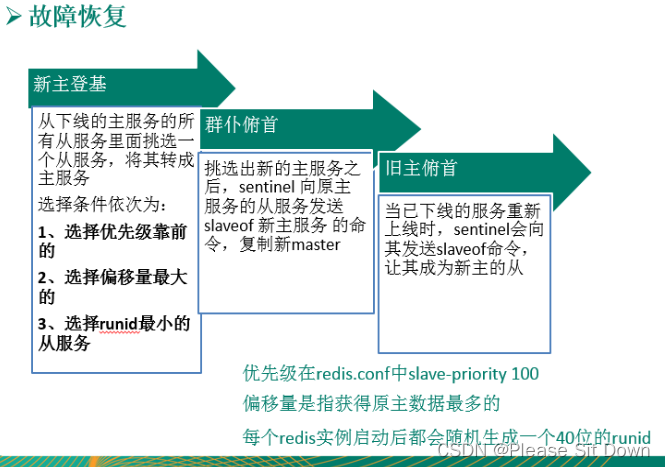
Redis 哨兵 (sentinel)
是什么 官网理论:https://redis.io/docs/management/sentinel/ 吹哨人巡查监控后台 master 主机是否故障,如果故障了根据投票数自动将某一个从库转换为新主库,继续对外服务。 作用:无人值守运维 哨兵的作用: 1…...

统计2021年10月每个退货率不大于0.5的商品各项指标
统计2021年10月每个退货率不大于0.5的商品各项指标_牛客题霸_牛客网s mysql(ifnull): select product_id, format(ifnull(sum(if_click)/nullif(count(*),0),0),3) as ctr, format(ifnull(sum(if_cart)/nullif(sum(if_click),0),0),3) as c…...
【小波尺度谱】从分段离散小波变换计算小波尺度谱研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
