七大经典比较排序算法
1. 插入排序 (⭐️⭐️)
🌟 思想:
直接插入排序是一种简单的插入排序法,思想是是把待排序的数据按照下标从小到大,依次插入到一个已经排好的序列中,直至全部插入,得到一个新的有序序列。例如:我们玩扑克牌的时候,每次摸进一张的新的牌我们会将其插入到合适的位置。
思路: 我们假设第一个数据有序,从第二个元素开始进行插入(最开始把前面第一个数据看作一个有序的区间),从后向前依次寻找合适位置,每次插入的时候如果当前位置不合适将当前位置向后移动一位。
InsertSort 实现:
// 插入排序
void InsertSort(int * nums , int size) {for (int i = 0; i < size - 1; i++) {// 把 [0 , end] 看作有序区间int end = i;// nums[end + 1]为需要插入的元素 使用 temp 保存int temp = nums[end + 1];// 找插入位置while (end >= 0 && temp < nums[end]) {// 把当前元素向后移动nums[end + 1] = nums[end];end--;}// 来到这里说明 temp >= nums[end] 找到插入位置// 插入nums[end + 1] = temp;}
}
我们可以思考一下极端情况:
- 假设数据为
3 5 7,end为1,temp = 7,所以temp < nums[end]为false循环结束,执行nums[end + 1] = temp,相当于nums[2] = 7而当前位置本来就是7,不会有影响。 - 假设数据为
3 5 1,end为1,temp = 1,当前temp < nums[end]将数据向后移动直至3 3 5,当end = -1循环结束,nums[end + 1] = temp相当于nums[0] = temp,所以最终结果为1 3 5。
总结:
- 元素结合越接近有序,直接插入排序算法的时间效率就越高。
- 最坏时间复杂度: O ( N 2 ) O(N^2) O(N2)
- 接近有序或已经有序时间复杂度: O ( N ) O(N) O(N)
- 空间复杂度: O ( 1 ) O(1) O(1)
2.希尔排序 (⭐️⭐️⭐️)
🌟 思想:
希尔排序又称缩小增量法。希尔排序的基本思想是:先选定一个 gap (整数),把待排序中的数据分成 gap 组(gap 距离的为同一组),并对每一组内的的数据进行插入排序。
假设 gap = 3 将下面的 10 个数分成 3 组。 {9 , 5 , 8 , 5}、{1 , 7 , 6}、{2 , 4 , 3}分别进行插入排序。当 gap 不为 1 时都是预排序,当 gap = 1时是插入排序,因为当数据接近有序的时候,插入排序的效率很高。

1️⃣ gap 组希尔排序: 这是希尔排序的 gap 组的一种写法,按上面的图来说,这样的写法是先走完红色组,再走蓝色组……
void ShellSort (int * nums , int size) {assert(nums);// 假设 gap = 3int gap = 3;for (int j = 0; j < gap; j++) {for (int i = j; i < size - gap; i+=gap) {int end = i;int temp = nums[end + gap];while (end >= 0 && temp < nums[end]) {nums[end + gap] = nums[end];end -= gap;}nums[end + gap] = temp;}}
}
2️⃣ gap 组希尔排序:第二种在上一种写法上进行了优化,原来是一组走完再走下一组,现在是一组一组间交替的去插入排序。
void ShellSort (int * nums , int size) {assert(nums);// 假设 gap = 3int gap = 3;for (int i = 0; i < size - gap; i++) {int end = i;int temp = nums[end + gap];while (end >= 0 && temp < nums[end]) {nums[end + gap] = nums[end];end -= gap;}nums[end + gap] = temp;}
}
ShellSort 实现:当 gap > 1 的时候都是预排序(是为了让数据更接近有序,因为直接插入排序当数据接近有序的时候是 O ( N ) O(N) O(N)),而这里 gap / 3 + 1 是为了最后一次让 gap = 1。 当 gap 越大的时候大的数会越快的到后面,但是数组越不接近有序。当 gap 越小的时候,数组越接近有序。当 gap = 1 就是直接插入排序。
void ShellSort (int * nums , int size) {assert(nums);int gap = size;while (gap > 1) {gap = gap / 3 + 1;for (int i = 0; i < size - gap; i++) {int end = i;int temp = nums[end + gap];while (end >= 0 && temp < nums[end]) {nums[end + gap] = nums[end];end -= gap;}nums[end + gap] = temp;}}
}
总结:
- 时间复杂度 ~ O ( N 1.3 ) O(N^{1.3}) O(N1.3)
- 空间复杂度: O ( 1 ) O(1) O(1)
- 希尔排序是插入排序的优化
3. 选择排序 (⭐️)
🌟 思想:
每一次从待排序的数据种选出最小或者最大的元素下标,存放在当前序列的起始位置,直到排序结束。
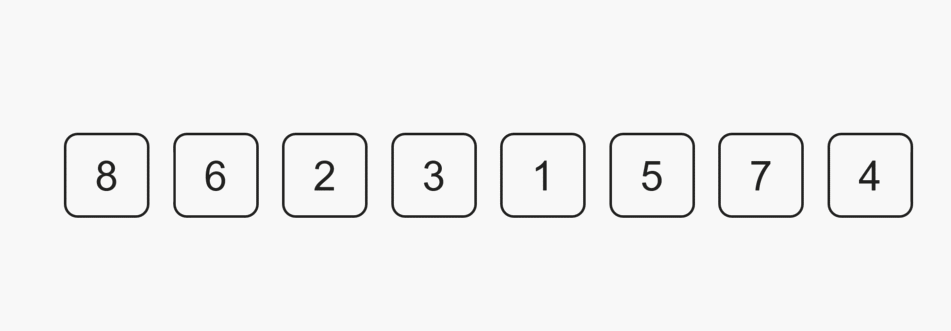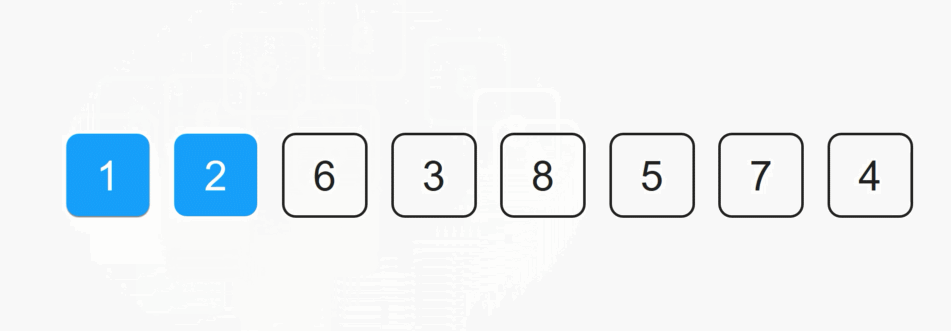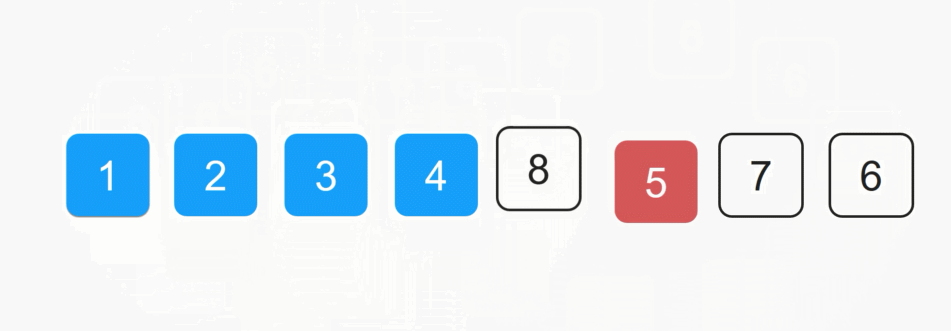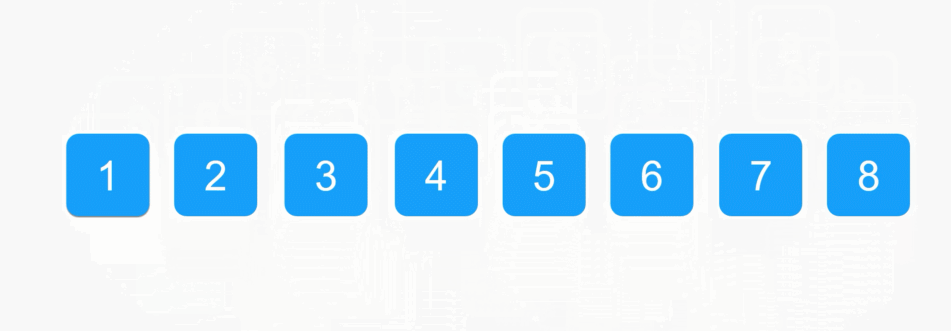
1️⃣SelectSort 实现:
// 选择排序
void SelectSort(int * nums , int size) {assert(nums);for (int i = 0; i < size - 1; i++) {int minIndex = i + 1;// 选数for (int j = i + 1; j < size; j++) {if (nums[j] < nums[minIndex ]) {minIndex = j;}}// 交换int temp = nums[minIndex];nums[minIndex] = nums[i];nums[i] = temp;}
}
2️⃣ SelectSort 优化: 我们可以同时选出两个数一个最大一个最小,把最小的组交换到当前区间的左边,最大的交换到区间的右边。
void SelectSort(int * nums , int size) {assert(nums);int left = 0;int right = size - 1;while (left < right) {// 最小值下标默认从左区间开始int maxIndex = left;int minIndex = left;for (int i = left + 1; i <= right; i++) {if (nums[i] > nums[maxIndex]) {maxIndex = i;}if (nums[i] < nums[minIndex]) {minIndex = i;}}// 交换Swap(&nums[left] , &nums[minIndex]);// 特殊情况:假设第一个位置就是最大值 那么做完第一次交换最小的值到最左边// 而最大值被交换到了原来最小值的位置if (left == maxIndex) {maxIndex = minIndex;}Swap(&nums[right] , &nums[maxIndex]);left++;right--;}
}
Swap 实现:
// 交换
void Swap(int* val1, int* val2) {int temp = *val1;*val1 = *val2;*val2 = temp;
}
总结:
- 选择排序比较好理解,但是效率很低,实际种很少使用。
- 时间复杂度 O ( N 2 ) O(N^2) O(N2)
4. 堆排序 (⭐️⭐️⭐️)
🌟 思想:
堆排序是指用堆这种数据结构所设计的一种排序思想,它是选择排序的一种,它是用堆来进行选数。升序需要建大堆,降序需要建小堆。
拿升序来举例,因为大堆的堆顶是最大的数,此时我们可以让堆顶和末尾元素交换。再让堆顶的元素向下调整(只不过此时向下调整,我们先让数组的长度减 1,因为最大的数已经到末尾的位置了,不必算入堆内)
AdjustDown 实现(大堆举例):
// 堆的向下调整算法
void AdjustDown(int * nums , int size , int parent) {assert(nums);// 默认左孩子最大int child = 2 * parent + 1;while (child < size) {// 选出左右孩子最大的孩子if (child + 1 < size && nums[child + 1] > nums[child]) {child++;}// 最大的孩子比父亲还大则调整if (nums[child] > nums[parent]) {Swap(&nums[child] , &nums[parent]);// 继续向下搜索parent = child;child = parent * 2 + 1;} else {break;}}
}
AdjustUp 实现(大堆举例):
// 堆的向上调整算法
void AdjustUp (int * nums , int child) {int parent = (child - 1) / 2;// 当孩子 = 0的时候已经没有父亲节点了while (child > 0) {if (nums[child] > nums[parent]) {Swap(&nums[child] , &nums[parent]);// 继续向上搜索child = parent;parent = (child - 1) / 2;} else {break;}}
}
HeapSort 实现:
// 堆排序
void HeapSort(int * nums , int size) {assert(nums);// 先建堆// 向上调整算法建堆// for (int i = 1; i < size; i++) {// AdjustUp(nums , i);// }// 向下调整算法建堆// 向下调整的前提是:左右子树必须都是堆// 所以大堆从第一个非叶子节点开始向下调整for (int parent = (size - 1 - 1) / 2; parent >= 0; parent--) {AdjustDown(nums , size , parent);}// 排序int end = size - 1;while (end > 0) {// 堆顶元素和末尾元素交换Swap(&nums[0] , &nums[end]); AdjustDown(nums , end , 0);end--;}
}
总结:
- 堆排序的时间复杂度 O ( N ∗ l o g N ) O(N*logN) O(N∗logN)
- 向上调整算法建堆的时间复杂度是 O ( N ∗ l o g N ) O(N * logN) O(N∗logN),向下调整算法建堆的时间复杂度是 O ( N ) O(N) O(N),但是向下调整算法建堆的前提是:当前左右子树必须是堆。所以向下调整算法要从非叶子节点开始向下调整,最后一个非叶子节点就是最后一个元素的父节点
(size - 1 - 1) / 2。
5. 冒泡排序 (⭐️⭐️)
🌟 思想:
冒泡排序是交换排序的一种。所谓交换就是根据序列中两个记录下标值的比较结果来对这一对数据进行交换,当第一躺冒泡排序结束后,若是升序会把最大的数冒到最后末尾,以此类推。
BubbleSort 实现:
// 冒泡排序
void BubbleSort(int* nums, int size) {assert(nums);for (int i = 0; i < size - 1; i++) {for (int j = 0; j < size - 1 - i; j++) {if (nums[j] > nums[j + 1]) {Swap(&nums[j] , &nums[j + 1]);}}}
}
BubbleSort 优化:当数组为有序的时候,我们用 enchage 来记录,若当前这一趟一次都没有交换,则数组已经有序。
// 冒泡排序
void BubbleSort(int* nums, int size) {assert(nums);for (int i = 0; i < size - 1; i++) {int exchage = 1;for (int j = 0; j < size - 1 - i; j++) {if (nums[j] > nums[j + 1]) {exchage = 0;Swap(&nums[j] , &nums[j + 1]);}}if (exchage) {break;}}
}
总结:
- 冒泡排序是非常经典的排序
- 时间复杂度 O ( N 2 ) O(N^2) O(N2)
6. 快速排序 (⭐️⭐️⭐️⭐️)
🌟 思想:
快速排序是 Hoare于1962年提出的一种二叉树结构的交换排序方法。基本思想是:从待排序序列中选一个 key(通常为最左边或者最右边),按照 key 把待排序序列分成两个子序列,左序列中的元素都 < key,右序列的元素都 > key,然后左右序列重复该过程,直到所有元素都排列在对应的位置上。

1.hoare版本:
思路和结论:假设 key 为最左边的数,那么就要先从右边走,再走左边。假设 key 为最右边的数,那么就要从左边先走,再走右边。这样做的目的是:当 left 与 right 相遇结束的时候,让 key 位置的元素与当前相遇位置交换,而当前相遇位置一定能保证比 key 要小(或大)。 第一次快速排序相当于处理好了第一个区间,因为 key 找到了合适的位置左面的数都比 key 小,右面的数都比 key 要大,此时只需要让左右区间重复上面的过程。左右区间划分为了 [begin , keyIndex - 1] keyIndex [keyIndex + 1 , end]。递归处理即可,当左右区间只剩一个数(begin == end)或者区间不存在(begin > end)的时候为递归结束条件。
QucikSort实现:
void QuickSort(int * nums , int begin , int end) {// 只剩一个数或者区间不存在不需要处理if (begin >= end) {return;}int left = begin;int right = end;// key 默认为最左边的数字int keyIndex = left;while (left < right) {// 右边先走,找小while (left < right && nums[right] >= nums[keyIndex]) {right--;}// 左边找大while (left < right && nums[left] <= nums[keyIndex]) {left++;}// 交换Swap(&nums[left] , &nums[right]);}// 相遇位置和 keyIndex 交换Swap(&nums[keyIndex] , &nums[left]);// 更改 keyIndexkeyIndex = left;QuickSort(nums , begin , keyIndex - 1);QuickSort(nums , keyIndex + 1, end);
}
💬 思考问题:
-
nums[left] <= nums[keyIndex]和nums[right] >= nums[keyIndex]这里为什么要使用=,不使用=可以吗?结论是不可以。
- 为什么右边和左边走的时候要加上
left < right?

- 为什么
key如果是左边的数就要先从右边走呢?左边先走可以吗?结论是不可以。

2.挖坑版本:
思路:先将最左面的数据存在一个临时变量 key 中,这样当前 key 这个位置就是一个坑位。右面 right 找小,找到之后把小的数填到当前坑中 nums[keyIndex] = nums[right],此时更换坑的位置 keyIndex = right。左面 left 找大,找到之后把大的数继续填到当前坑中 nums[keyIndex] = nums[left],此时继续更换坑的位置 keyIndex = left。当 left 与 right 相遇时在把 key 填入相遇(坑位)位置。
QucikSort实现:
void QuickSort(int * nums , int begin , int end) {// 只剩一个数或者区间不存在不需要处理if (begin >= end) {return;}int left = begin;int right = end;// 保存当前坑的元素int key= nums[left];// 坑位int keyIndex = left;while (left < right) {while (left < right && nums[right] >= key) {right--;}// 填坑nums[keyIndex] = nums[right];// 更换坑的位置keyIndex = right;while (left < right && nums[left] <= key) {left++;}// 填坑nums[keyIndex] = nums[left];// 更换坑的位置keyIndex = left;}// 循环结束填入当前坑位nums[keyIndex] = key;QuickSort(nums , begin , keyIndex - 1);QuickSort(nums , keyIndex + 1, end);
}
注:同样一组数,使用 hoare 思想和挖坑法思想进行一轮快排的结果是不同的。
例如:{6 , 1 , 2 , 7 , 9 , 3 , 4 , 5 , 10 , 8}
-
hoare:第一次交换{6 , 1 , 2 , 5 , 9 , 3 , 4 , 7 , 10 , 8}、第二次交换{6 , 1 , 2 , 5 , 4 , 3 , 9 , 7 , 10 , 8}、循环结束相遇位置与keyIndex位置交换{3 , 1 , 2 , 5 , 4 , 6 , 9 , 7 , 10 , 8}最终结果。 -
挖坑法:第一次挖坑{5 , 1 , 2 , 7 , 9 , 3 , 4 , (5) , 10 , 8}、第二次{5 , 1 , 2 , (7) , 9 , 3 , 4 , 7 , 10 , 8}、第三次{5 , 1 , 2 , 4 , 9 , 3 , (4) , 7 , 10 , 8}、第四次{5 , 1 , 2 , 4 , (9) , 3 , 9 , 7 , 10 , 8}、第五次{5 , 1 , 2 , 4 , 3 , (3) , 9 , 7 , 10 , 8}、循环结束把当前坑位填入key最终结果是{5 , 1 , 2 , 4 , 3 , 6 , 9 , 7 , 10 , 8}。
3.前后指针版本:
思路: 定义一个 prev 和 cur,cur 找比 key 要小的数,若找到则 ++prev 和 cur 当前下标的元素进行交换,这样做有一种把小的数翻到前面来,大的往后推。而 prev 后面的数都要比 key 大,最终 cur 越界循环结束,再把 keyIndex 位置和 prev 位置的元素进行交换。
QucikSort 实现:
void QuickSort(int * nums , int begin , int end) {// 只剩一个数或者区间不存在不需要处理if (begin >= end) {return;}int prev = begin;int cur = prev + 1;int keyIndex = begin;while (cur <= end) {if (nums[cur] < nums[keyIndex] && ++prev != cur) {Swap(&nums[prev] , &nums[cur]);}cur++;}Swap(&nums[prev] , &nums[keyIndex]);keyIndex = prev;QuickSort(nums , begin , keyIndex - 1);QuickSort(nums , keyIndex + 1, end);
}
🌟 快排优化
💬 为什么要优化?
因为 key 会影响快排的效率,如果每次的 key 都是中间那个值那么每次都是二分,若每次的 key 都是最小的,最坏情况下快排的时间复杂度 O ( N 2 ) O(N^2) O(N2)。最大的问题是会引起 栈溢出。
1.三数取中优化:
思路: 第一个数和中间还有最后的数,选不是最大也不是最小的数。三数取中主要体现在数据已经有序的情况下。
getMidIndex 实现:
int getMidIndex(int* nums, int begin, int end) {int midIndex = (begin + end) / 2;if (nums[begin] > nums[midIndex]) {// nums[begin] > nums[minIndex]if (nums[midIndex] > nums[end]) {// nums[begin] > nums[minIndex] > nums[end]return midIndex;}else if (nums[begin] > nums[end]) {// nums[begin] > nums[minIndex]// nums[end] >= nums[minIndex]// nums[begin] > nums[end]return end;}else {// nums[begin] > nums[minIndex]// nums[end] >= nums[minIndex]// nums[begin] <= nums[end]return begin;}}else {// nums[begin] <= nums[minIndex]if (nums[begin] > nums[end]) {// nums[begin] <= nums[minIndex]// nums[begin] > nums[end]return begin;}else if (nums[midIndex] > nums[end]) {// nums[begin] <= nums[minIndex]// nums[begin] <= nums[end]// nums[minIndex] > nums[end]return end;}else {// nums[begin] <= nums[minIndex]// nums[begin] <= nums[end]// nums[minIndex] <= nums[end]return midIndex;}}
}
2.小区间优化:
思路: 若只剩最后 10 - 20 个数,还使用快速排序的递归就有点不太划算了。所以当区间较小的时候,就不再使用递归继续划分小区间。考虑直接用其他排序对小区间处理,而希尔排序和堆排序对于数据量小的时候也不太优,所以在简单排序中,插入排序适应性最强。 小区间优化体现在减少递归的调用次数。
QuickSort 优化实现:
void QuickSort(int* nums, int begin, int end) {// 只剩一个数或者区间不存在不需要处理if (begin >= end) {return;}if (end - begin > 15) {int prev = begin;int cur = prev + 1;int keyIndex = begin;// 三数取中优化int midIndex = getMidIndex(nums, begin, end);Swap(&nums[keyIndex], &nums[midIndex]);while (cur <= end) {if (nums[cur] < nums[keyIndex] && ++prev != cur) {Swap(&nums[prev], &nums[cur]);}cur++;}Swap(&nums[prev], &nums[keyIndex]);keyIndex = prev;QuickSort(nums, begin, keyIndex - 1);QuickSort(nums, keyIndex + 1, end);} else {// 小区间优化// 插入排序InsertSort(nums + begin , end - begin + 1);}
}
🌟 快排非递归
QuickSortNoneR 非递归实现:
// 快排非递归(使用栈)
void QucikSortNoneR(int* nums, int begin, int end) {assert(nums);Stack stack;StackInit(&stack);// 区间进栈StackPush(&stack , end);StackPush(&stack, begin);while (!StackEmpty(&stack)) {// 取出左右区间int left = StackTop(&stack);StackPop(&stack);int right = StackTop(&stack);StackPop(&stack);// 快排int keyIndex = left;int prev = left;int cur = prev + 1;while (cur <= right) {if (nums[cur] < nums[keyIndex] && ++prev != cur) {Swap(&nums[prev], &nums[cur]);}cur++;}Swap(&nums[prev], &nums[keyIndex]);keyIndex = prev;// [left , keyIndex - 1] keyIndex [keyIndex + 1 , right]if (keyIndex + 1 < right) {// 区间存在 入栈StackPush(&stack, right);StackPush(&stack, keyIndex + 1);}if (left < keyIndex - 1) {// 区间存在 入栈StackPush(&stack, keyIndex - 1);StackPush(&stack, left);}}StackDestroy(&stack);
}
总结:
- 时间复杂度 O ( N ∗ l o g N ) O(N*logN) O(N∗logN)
- 空间复杂度 O ( l o g N ) O(logN) O(logN)
7. 归并排序 (⭐️⭐️⭐️)
🌟 思想:
归并排序是建立在归并操作上的一种有效的排序算法,是分治的一个典型的应用。将两个有序的子序列归并得到完全有序的序列。归并排序要借助额外的空间。
MergeSort 递归实现:
void merge(int* nums, int begin, int end, int* temp) {// 区间只有一个数或者不存在if (begin >= end) {return;}int midIndex = (begin + end) / 2;// [begin , midIndex] [minIndex + 1 , end]merge(nums , begin , midIndex , temp);merge(nums , midIndex + 1 , end , temp);// 归并int leftBegin = begin;int leftEnd = midIndex;int rightBegin = midIndex + 1;int rightEnd = end;int i = leftBegin;while (leftBegin <= leftEnd && rightBegin <= rightEnd) {if (nums[leftBegin] < nums[rightBegin]) {temp[i++] = nums[leftBegin++];}else {temp[i++] = nums[rightBegin++];}}// 左区间还存在while (leftBegin <= leftEnd) {temp[i++] = nums[leftBegin++];}// 右区间还存在while (rightBegin <= rightEnd) {temp[i++] = nums[rightBegin++];}// 拷贝回原数组memcpy(nums + begin , temp + begin, (end - begin + 1) * sizeof(int));
}// 归并排序
void MergeSort(int* nums, int size) {assert(nums);int* temp = (int*)malloc(sizeof(int) * size);assert(temp);merge(nums , 0 , size - 1 , temp);free(temp);
}
🌟 归并非递归
MergeSort 非递归实现:
// 归并排序非递归
void MergeSortNoneR(int* nums, int size) {assert(nums);int* temp = (int*)malloc(sizeof(int) * size);assert(temp);int gap = 1;while (gap < size) {for (int i = 0; i < size; i += 2 * gap) {int leftBegin = i;int leftEnd = i + gap - 1;int rightBegin = i + gap;int rightEnd = i + 2 * gap - 1;// 检查边界if (leftEnd >= size) {// 修正左区间leftEnd = size - 1;// 让右区间不存在rightBegin = size + 1;rightEnd = size;}else if (rightBegin >= size) {rightBegin = size + 1;rightEnd = size;}else if (rightEnd >= size) {rightEnd = size - 1;}// 归并int j = leftBegin;while (leftBegin <= leftEnd && rightBegin <= rightEnd) {if (nums[leftBegin] < nums[rightBegin]) {temp[j++] = nums[leftBegin++];}else {temp[j++] = nums[rightBegin++];}}// 左区间还存在while (leftBegin <= leftEnd) {temp[j++] = nums[leftBegin++];}// 右区间还存在while (rightBegin <= rightEnd) {temp[j++] = nums[rightBegin++];}}memcpy(nums, temp, sizeof(int) * size);gap *= 2;}free(temp);
}
总结:
- 时间复杂度 O ( N ∗ l o g N ) O(N*logN) O(N∗logN)
- 空间复杂度 O ( N ) O(N) O(N)
相关文章:

七大经典比较排序算法
1. 插入排序 (⭐️⭐️) 🌟 思想: 直接插入排序是一种简单的插入排序法,思想是是把待排序的数据按照下标从小到大,依次插入到一个已经排好的序列中,直至全部插入,得到一个新的有序序列。例如:…...
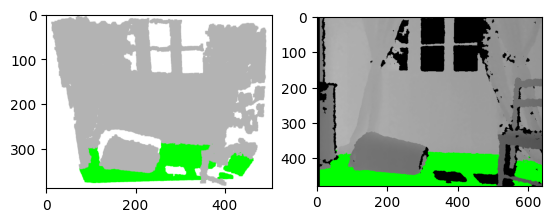
【点云处理教程】03使用 Python 实现地面检测
一、说明 这是我的“点云处理”教程的第3篇文章。“点云处理”教程对初学者友好,我们将在其中简单地介绍从数据准备到数据分割和分类的点云处理管道。 在上一教程中,我们在不使用 Open3D 库的情况下从深度数据计算点云。在本教程中,我们将首先…...
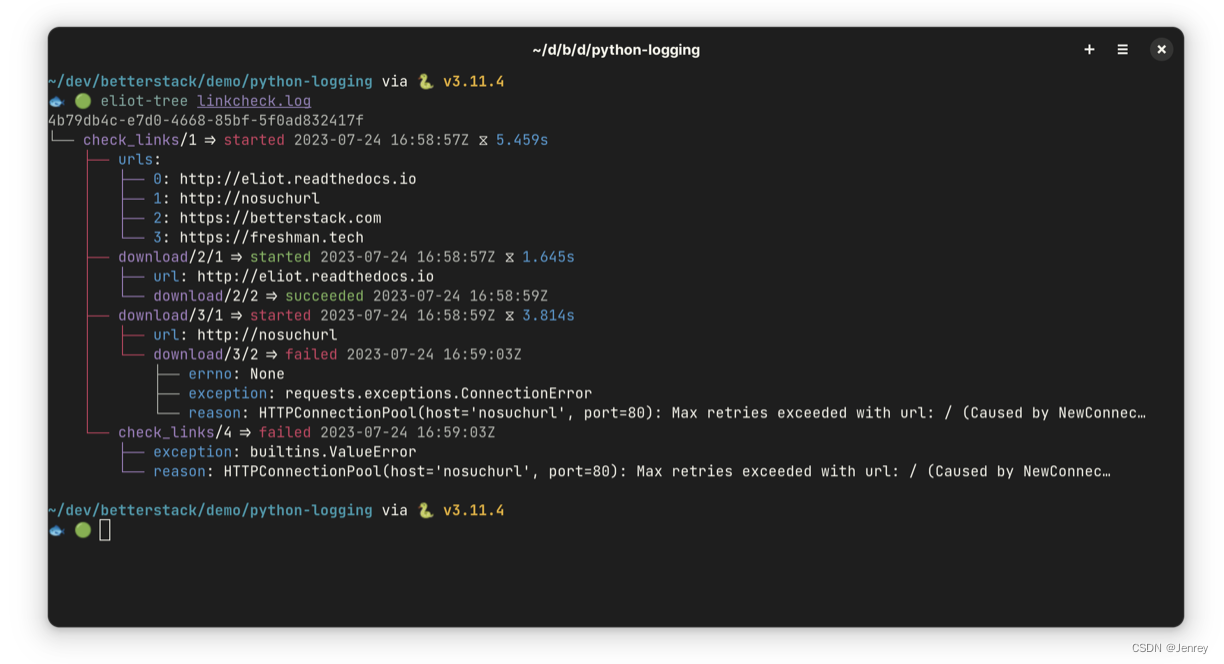
Python 日志记录:6大日志记录库的比较
Python 日志记录:6大日志记录库的比较 文章目录 Python 日志记录:6大日志记录库的比较前言一些日志框架建议1. logging - 内置的标准日志模块默认日志记录器自定义日志记录器生成结构化日志 2. Loguru - 最流行的Python第三方日志框架默认日志记录器自定…...

最近遇到一些问题的解决方案
最近遇到一些问题的解决方案 SpringBoot前后端分离参数传递方式总结Java8版本特性讲解idea使用git更新代码 : update project removeAll引发得java.lang.UnsupportedOperationException异常Java的split()函数用多个不同符号分割 Aspect注解切面demo 抽取公共组件,使…...

封装hutool工具生成JWT token
private static final String KEY "abcdef";/*** 生成token** param payload 可以存放用户的一些信息,不要存放敏感字段* return*/public static String createToken(Map<String, Object> payload) {//十分重要,不禁用发布到生产环境无…...

【手机】三星手机刷机解决SecSetupWizard已停止
三星手机恢复出厂设置之后,出现SecSetupWizard已停止的解决方案 零、问题 我手上有一部同学给的三星 GT-S6812I,这几天搞了张新卡,多余出的卡就放到这个手机上玩去了。因为是获取了root权限的(直接使用KingRoot就可以࿰…...

GDAL C++ API 学习之路 OGRGeometry 抽象曲线基类 OGRCurve
OGRCurve class "ogrsf_frmts.h" OGRCurve 是 OGR(OpenGIS Simple Features Reference Implementation)几何库中的一个基类,表示曲线几何对象。它是 OGRLineString 和 OGRCircularString 的抽象基类,用于表示曲…...

etcd底层支持的数据库有哪些
etcd底层的数据库可以更换。在当前版本的etcd中,它使用的是BoltDB作为默认的后端存储引擎。但是,etcd提供了接口允许您更换数据库后端,以便根据需要选择更合适的存储引擎。 以下是etcd支持的一些后端数据库选项: BoltDBÿ…...
linux设备驱动的poll与fasync
什么是fasync 在 Linux 驱动程序中,fasync 是一种机制,用于在异步事件发生时通知进程。它允许进程在等待设备事件时,不必像传统的轮询方式那样持续地查询设备状态。 具体来说,当进程调用 fcntl(fd, F_SETFL, O_ASYNC) 函数时&am…...
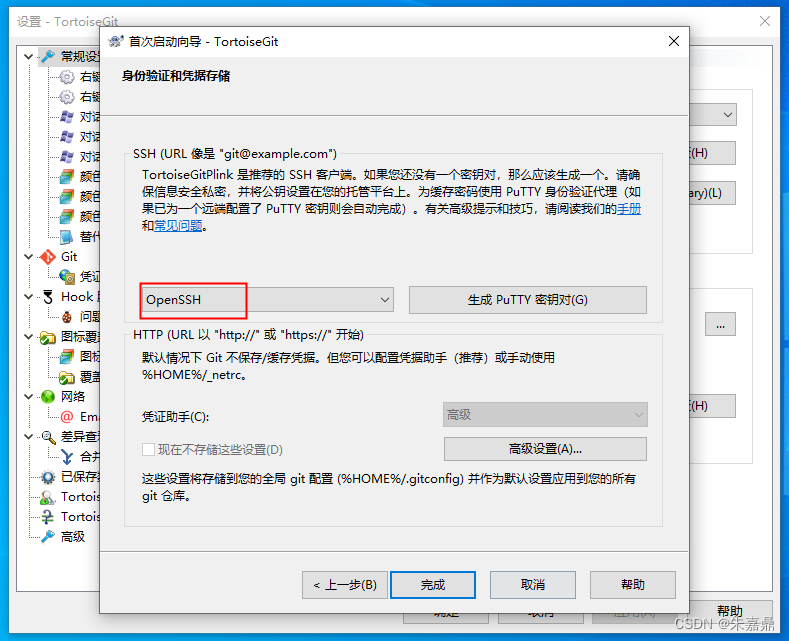
TortoiseGit安装与配置
注:在安装TortoiseGit之前我已经安装了git工具。 二、Git的诞生及环境配置_tortoisegit安装包_朱嘉鼎的博客-CSDN博客 1、TortoiseGit简介 TortoiseGit是基于TortoiseSVN的Git版本的Windows Shell界面。它是开源的,可以完全免费使用。 TortoiseGit 支持…...
)
Java代码打印空心菱形(小练习)
回看基础 利用Java代码打印一个空心菱形 //5. 打印空心菱形 import java.util.Scanner; public class MulForExercise01 {//编写一个 main 方法public static void main(String[] args) {Scanner myScanner new Scanner(System.in);System.out.println("请输入正三角的行…...

【性能优化】MySQL百万数据深度分页优化思路分析
业务场景 一般在项目开发中会有很多的统计数据需要进行上报分析,一般在分析过后会在后台展示出来给运营和产品进行分页查看,最常见的一种就是根据日期进行筛选。这种统计数据随着时间的推移数据量会慢慢的变大,达到百万、千万条数据只是时间问…...
交叉编译工具链的安装、配置、使用
一、交叉编译的概念 交叉编译是在一个平台上生成另一个平台上的可执行代码。 编译:一个平台上生成在该平台上的可执行文件。 例如:我们的Windows上面编写的C51代码,并编译成可执行的代码,如xx.hex.在C51上面运行。 我们在Ubunt…...
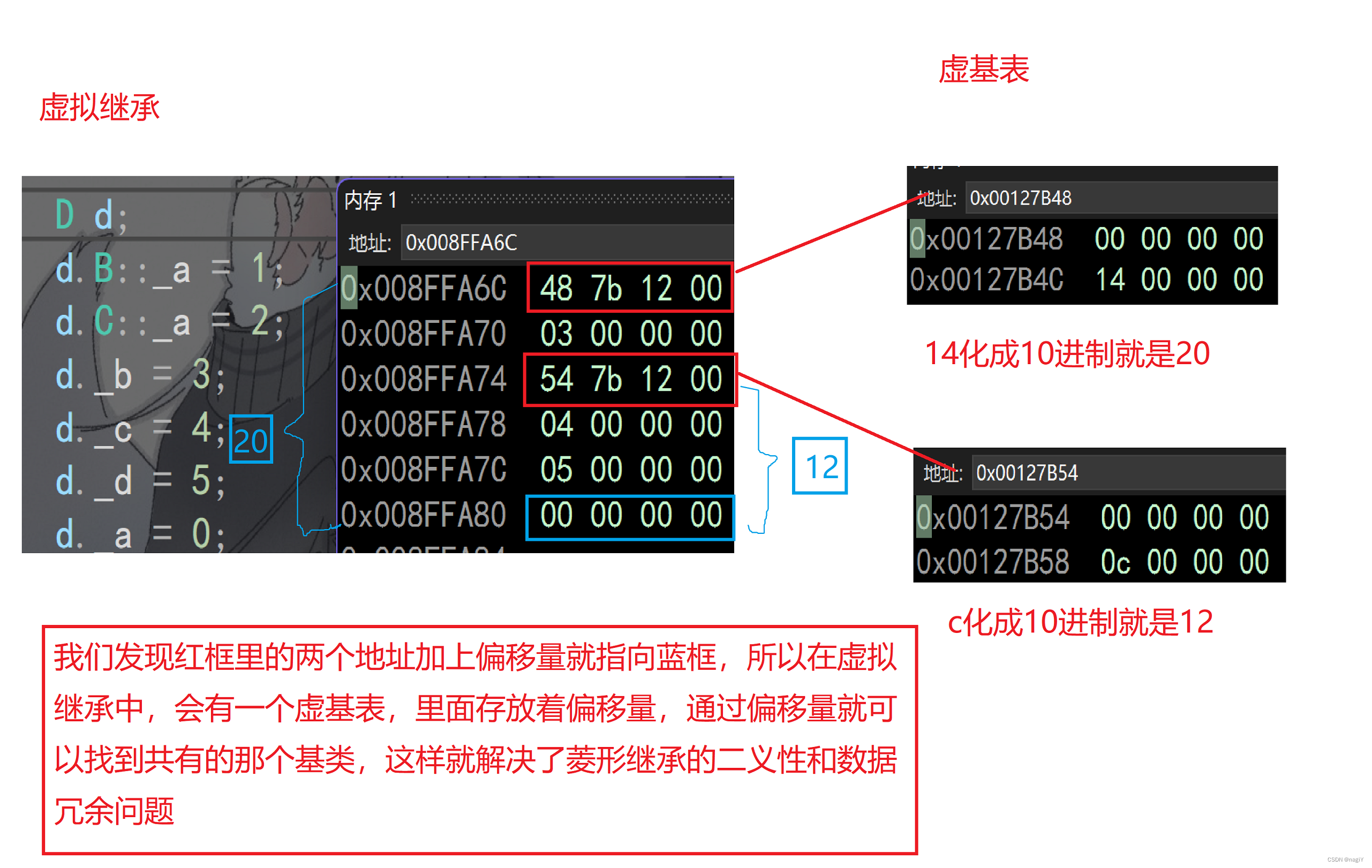
【C++ 进阶】继承
一.继承的定义格式 基类又叫父类,派生类又叫子类; 二.继承方式 继承方式分为三种: 1.public继承 2.protected继承 3.private继承 基类成员与继承方式的关系共有9种,见下表: 虽然说是有9种,但其实最常用的还…...
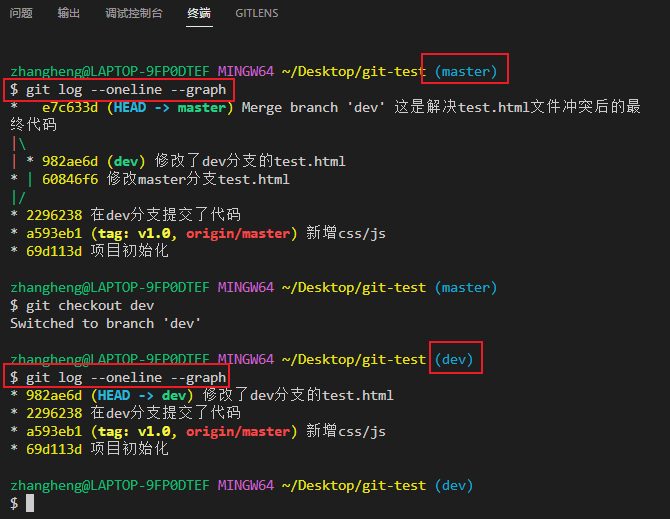
Git使用详细教程
1. cmd面板的常用命令 clear:清屏cd 文件夹名称----进入文件夹cd … 进入上一级目录(两个点)dir 查看当前目录下的文件和文件夹(全拼:directory)Is 查看当前目录下的文件和文件夹touch 文件名----创建文件echo 内容 > 创建文件名----创建文件并写入内容rm 文件名…...

小程序 表单验证
使用 WxValidate.js 插件来校验表单数据 常用实例方法 名称返回类型描述checkForm(e)boolean验证所有字段的规则,返回验证是否通过。valid()boolean返回验证是否通过。size()number返回错误信息的个数。validationErrors()array返回所有错误信息。addMethod(name…...
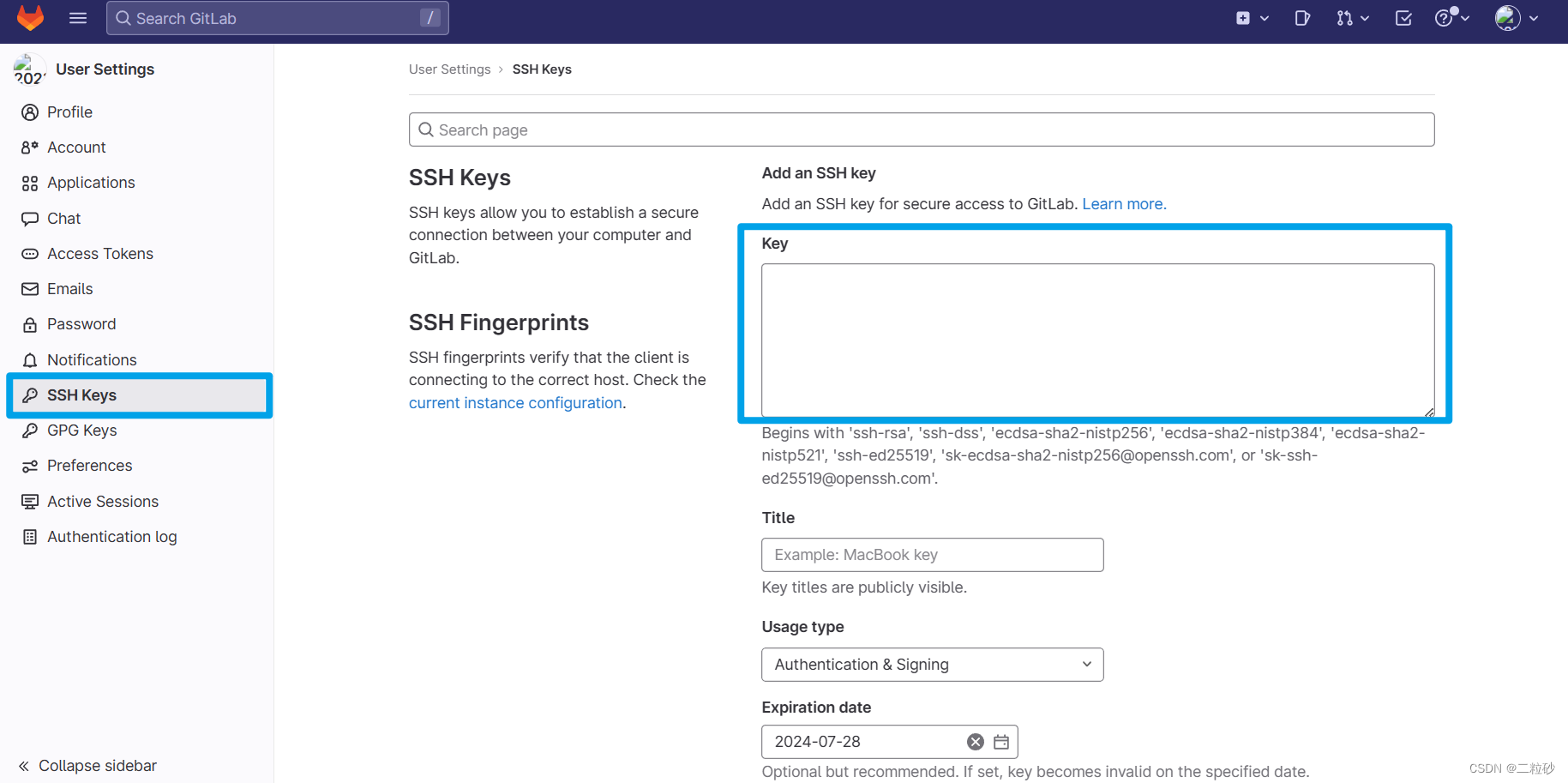
本地仓库推送至远程仓库
1. 本地生成ssh密钥对 ssh-keygen -t rsa -C 邮箱2. 添加公钥到gitlab/github/gitee上 打开C:\Users\用户名\.ssh目录下生成的密钥文件id_rsa.pub,把内容复制到如下文本框中 删除Expiration date显示的日期,公钥有效期变成永久,之后点Add K…...
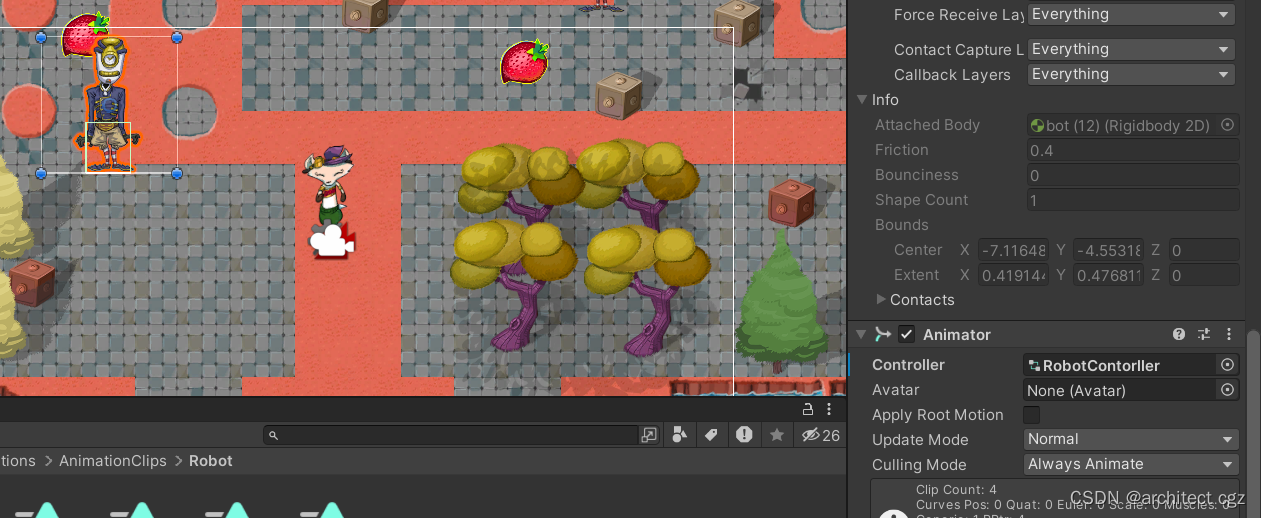
【Unity2D】角色动画的切换
动画状态转换 第一种方法是设置一个中间状态,从中间状态向其余各种状态切换,且各状态向其他状态需要设置参数 实现动作转移时右键点击Make Transition即可 实现动画转移需要设置条件 点击一种动画到另一种动画的线 ,然后点击加号添加Condi…...
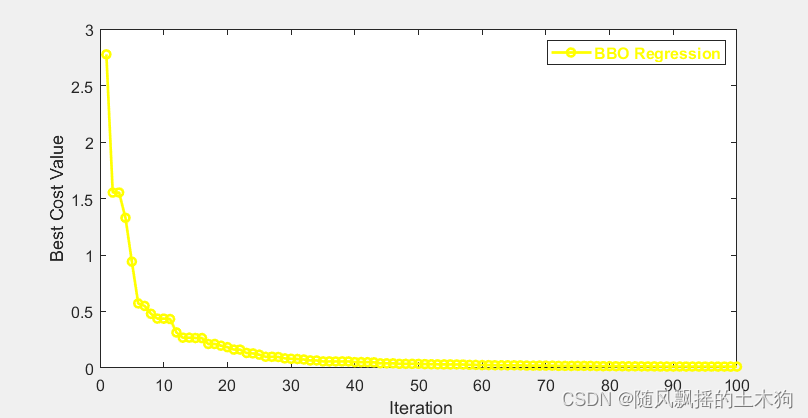
【MATLAB第62期】基于MATLAB的PSO-NN、BBO-NN、前馈神经网络NN回归预测对比
【MATLAB第62期】基于MATLAB的PSO-NN、BBO-NN、前馈神经网络NN回归预测对比 一、数据设置 1、7输入1输出 2、103行样本 3、80个训练样本,23个测试样本 二、效果展示 NN训练集数据的R2为:0.73013 NN测试集数据的R2为:0.23848 NN训练集数据的…...
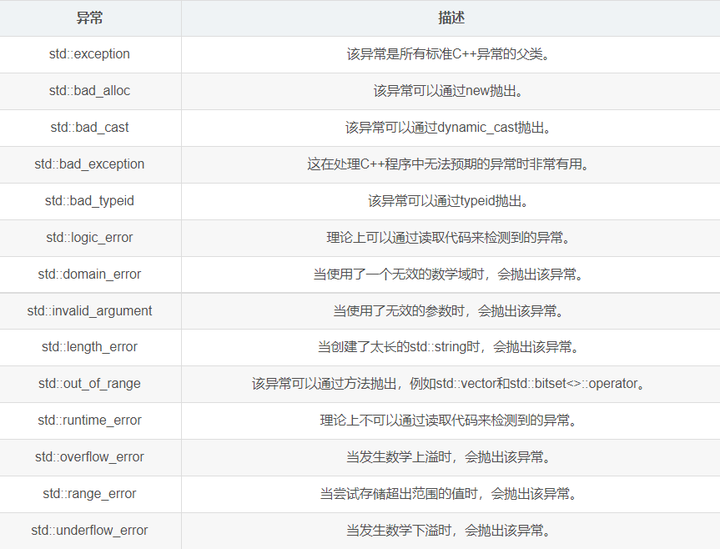
深度剖析C++ 异常机制
传统排错 我们早在 C 程序里面传统的错误处理手段有: 终止程序,如 assert;缺陷是用户难以接受,说白了就是一种及其粗暴的手法,比如发生内存错误,除0错误时就会终止程序。 返回错误码。缺陷是需要我们自己…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
