【MATLAB第58期】基于MATLAB的PCA-Kmeans、PCA-LVQ与BP神经网络分类预测模型对比
【MATLAB第58期】基于MATLAB的PCA-Kmeans、PCA-LVQ与BP神经网络分类预测模型对比
一、数据介绍
基于UCI葡萄酒数据集进行葡萄酒分类及产地预测
共包含178组样本数据,来源于三个葡萄酒产地,每组数据包含产地标签及13种化学元素含量,即已知类别标签。
把样本集随机分为训练集和测试集(70%训练,30%测试),根据已有数据集训练一个能进行葡萄酒产地预测的模型,以正确区分三个产地所产出的葡萄酒,
分别采用PCA+Kmeans、PCA+LVQ、BP神经网络等方法进行模型的训练与测试,准确率都能达到95%左右。
二、效果展示
1.PCA-Kmeans
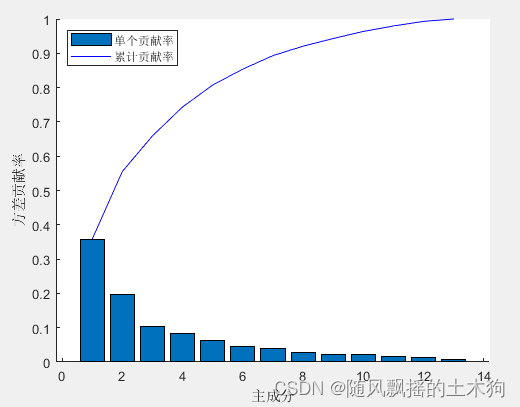
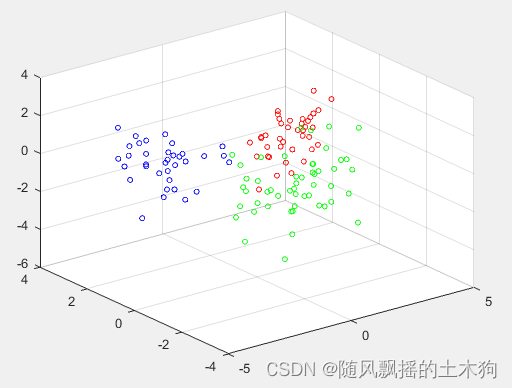
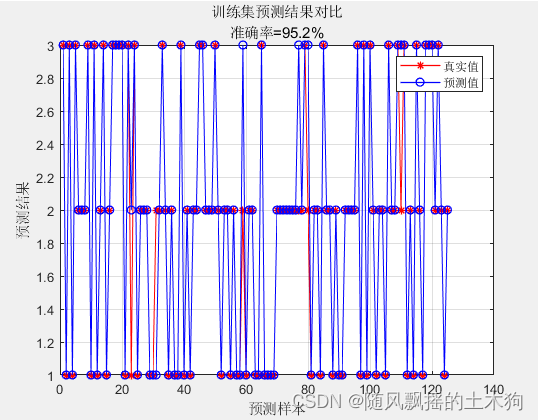
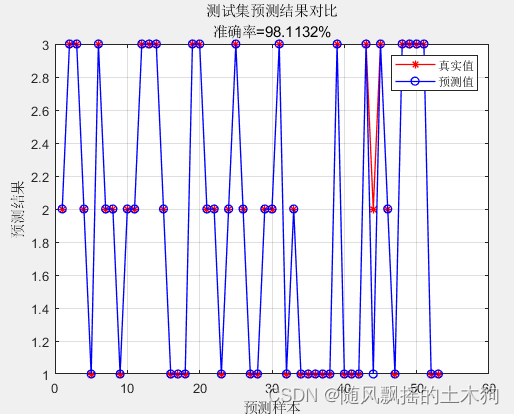
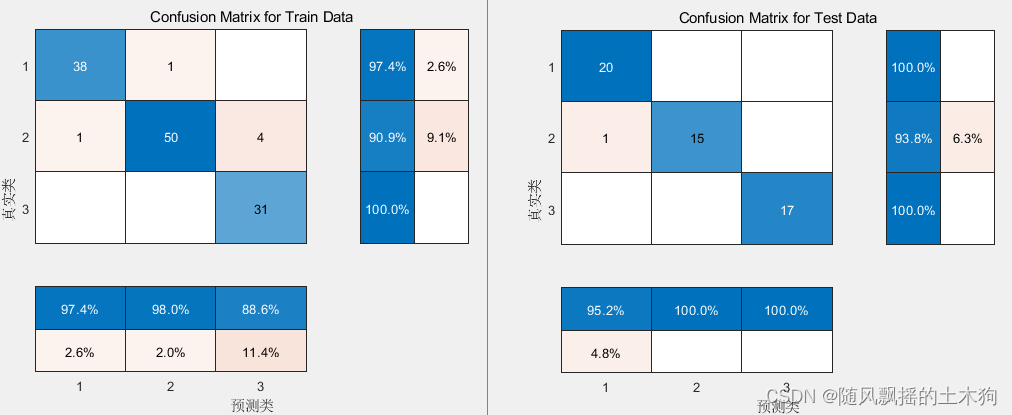
train_accuracy = 0.95
test_accuracy = 0.98
2.PCA-LVQ
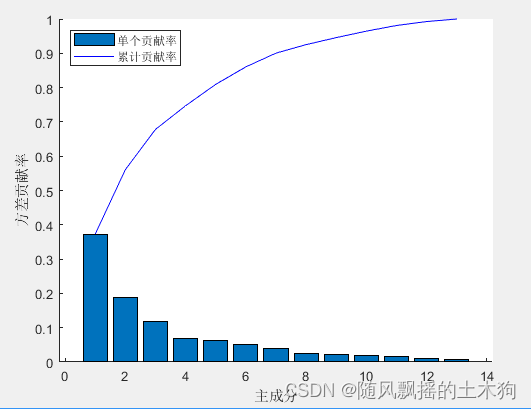
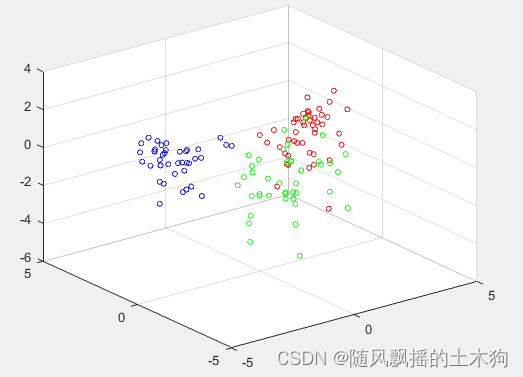
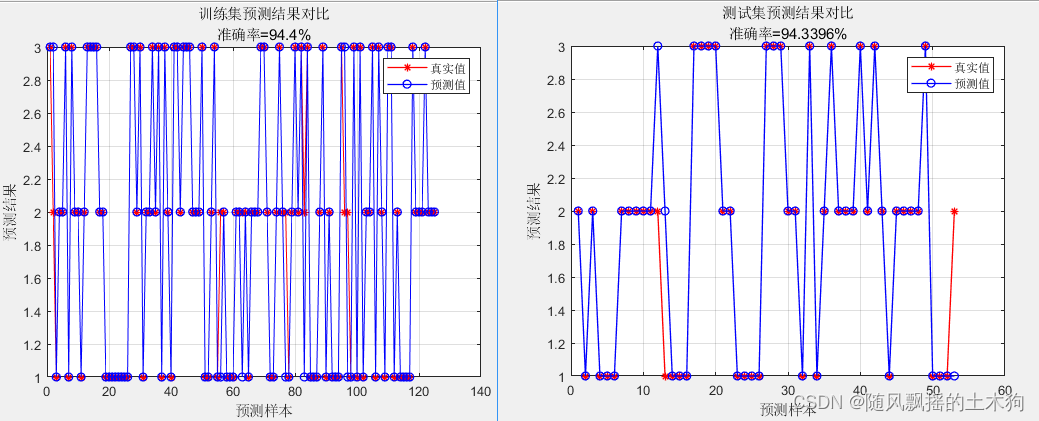
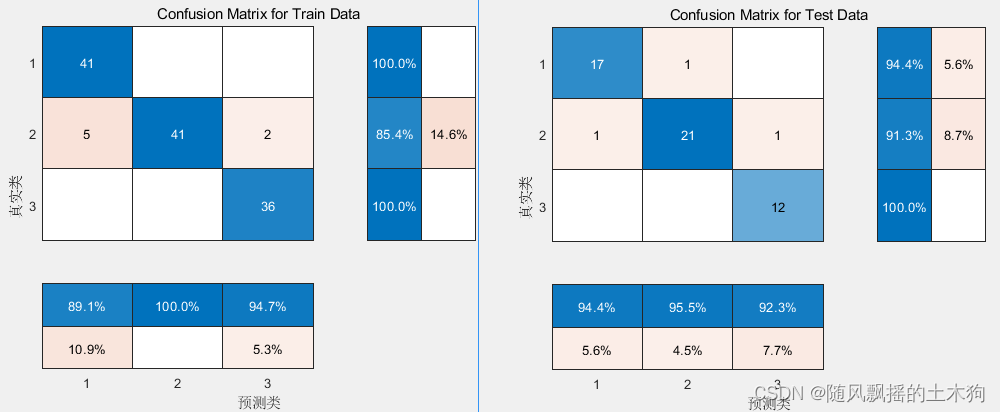
3.BP
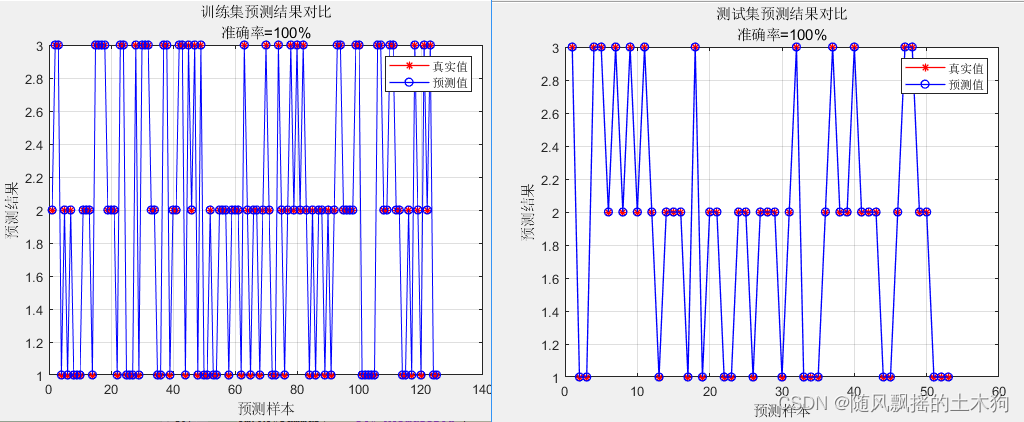
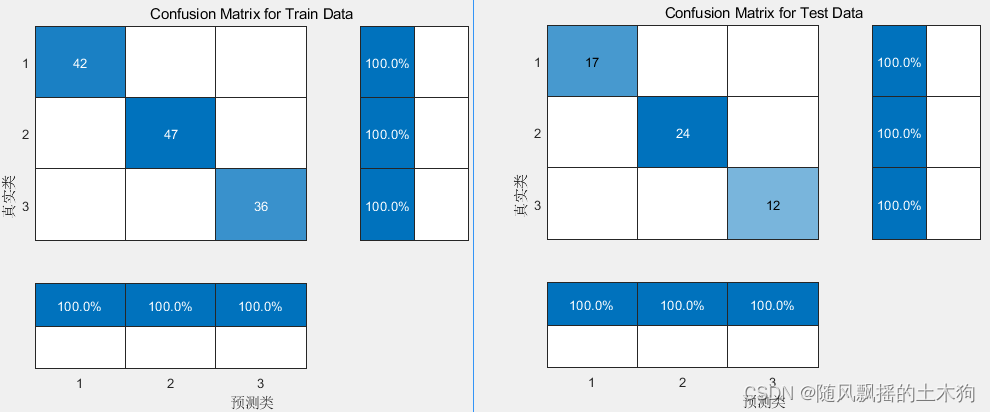
三、代码展示(部分代码)
clear all;
wine_data = xlsread('wine.xlsx'); %分类标签默认第一列method = 'BP';%PK: PCA & Kmeans
%PL: PCA & LVQ
%BP: BP Neural Network'
rate = 0.7;%训练集70%,测试集30%
N = size(unique(wine_data(:,1)),1);;total_cnt = size(wine_data,1);
train_cnt = round(total_cnt*rate);
test_cnt = total_cnt - train_cnt;rand_idx = randperm(total_cnt);
train_idx = rand_idx(1:train_cnt);
test_idx = rand_idx(train_cnt+1:total_cnt);train_data = wine_data(train_idx,2:size(wine_data,2));
train_class = wine_data(train_idx,1);
test_data = wine_data(test_idx,2:size(wine_data,2));
test_class = wine_data(test_idx,1);
dim = size(wine_data,2)-1;%矩阵z-score标准化
train_SM = zeros(train_cnt,dim);
data_mean = mean(train_data);
data_std = std(train_data);
test_SM = zeros(test_cnt,dim);
for j = 1:dimtrain_SM(:,j) = (train_data(:,j) - data_mean(j)) / data_std(j);test_SM(:,j) = (test_data(:,j) - data_mean(j)) / data_std(j);
end
四、代码获取
私信回复“58期”即可获取下载链接。
相关文章:

【MATLAB第58期】基于MATLAB的PCA-Kmeans、PCA-LVQ与BP神经网络分类预测模型对比
【MATLAB第58期】基于MATLAB的PCA-Kmeans、PCA-LVQ与BP神经网络分类预测模型对比 一、数据介绍 基于UCI葡萄酒数据集进行葡萄酒分类及产地预测 共包含178组样本数据,来源于三个葡萄酒产地,每组数据包含产地标签及13种化学元素含量,即已知类…...
CF1833 A-E
A题 题目链接:https://codeforces.com/problemset/problem/1833/A 基本思路:for循环遍历字符串s,依次截取字符串s的子串str,并保存到集合中,最后输出集合内元素的数目即可 AC代码: #include <iostrea…...

【深度学习】【Image Inpainting】Generative Image Inpainting with Contextual Attention
Generative Image Inpainting with Contextual Attention DeepFillv1 (CVPR’2018) 论文:https://arxiv.org/abs/1801.07892 论文代码:https://github.com/JiahuiYu/generative_inpainting 论文摘录 文章目录 效果一览摘要介绍论文贡献相关工作Image…...
二维深度卷积网络模型下的轴承故障诊断
1.数据集 使用凯斯西储大学轴承数据集,一共有4种负载下采集的数据,每种负载下有10种 故障状态:三种不同尺寸下的内圈故障、三种不同尺寸下的外圈故障、三种不同尺寸下的滚动体故障和一种正常状态 2.模型(二维CNN) 使…...

redis突然变慢问题定位
CPU 相关:使用复杂度过高命令、O(N)的这个N,数据的持久化,都与耗费过多的 CPU 资源有关 内存相关:bigkey 内存的申请和释放、数据过期、数据淘汰、碎片整理、内存大页、内存写时复制都与内存息息相关 磁盘…...
React井字棋游戏官方示例
在本篇技术博客中,我们将介绍一个React官方示例:井字棋游戏。我们将逐步讲解代码实现,包括游戏的组件结构、状态管理、胜者判定以及历史记录功能。让我们一起开始吧! 项目概览 在这个井字棋游戏中,我们有以下组件&am…...

七大经典比较排序算法
1. 插入排序 (⭐️⭐️) 🌟 思想: 直接插入排序是一种简单的插入排序法,思想是是把待排序的数据按照下标从小到大,依次插入到一个已经排好的序列中,直至全部插入,得到一个新的有序序列。例如:…...
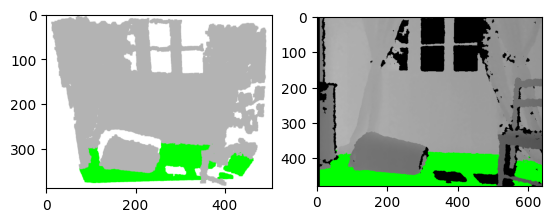
【点云处理教程】03使用 Python 实现地面检测
一、说明 这是我的“点云处理”教程的第3篇文章。“点云处理”教程对初学者友好,我们将在其中简单地介绍从数据准备到数据分割和分类的点云处理管道。 在上一教程中,我们在不使用 Open3D 库的情况下从深度数据计算点云。在本教程中,我们将首先…...
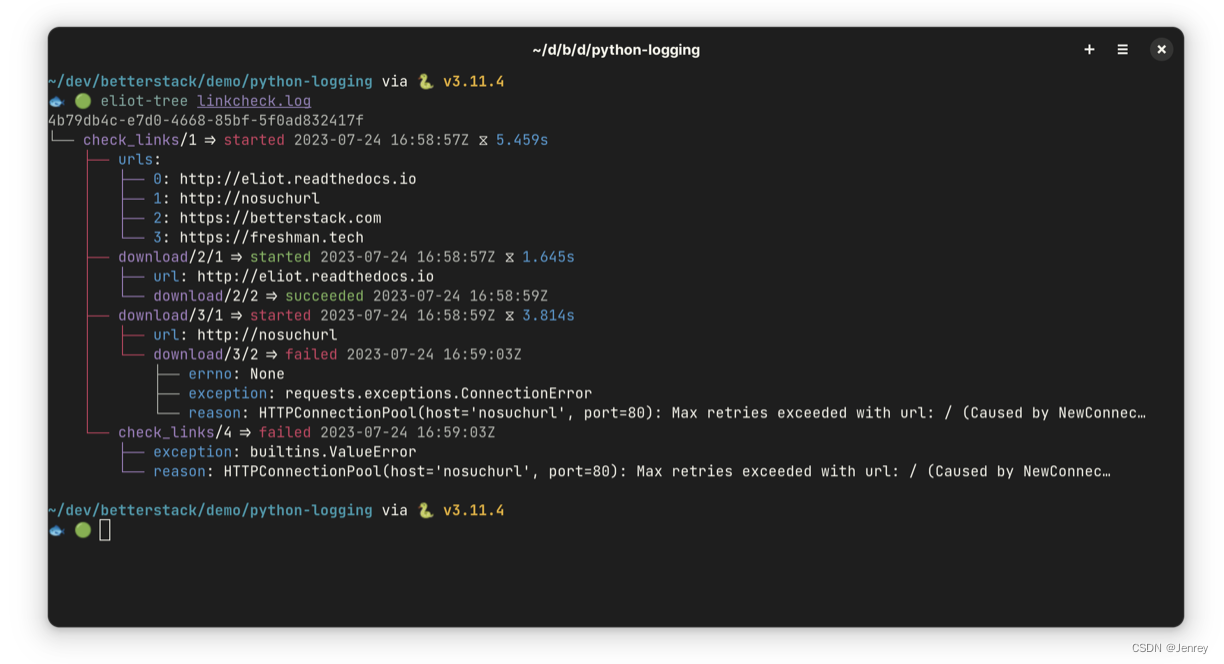
Python 日志记录:6大日志记录库的比较
Python 日志记录:6大日志记录库的比较 文章目录 Python 日志记录:6大日志记录库的比较前言一些日志框架建议1. logging - 内置的标准日志模块默认日志记录器自定义日志记录器生成结构化日志 2. Loguru - 最流行的Python第三方日志框架默认日志记录器自定…...

最近遇到一些问题的解决方案
最近遇到一些问题的解决方案 SpringBoot前后端分离参数传递方式总结Java8版本特性讲解idea使用git更新代码 : update project removeAll引发得java.lang.UnsupportedOperationException异常Java的split()函数用多个不同符号分割 Aspect注解切面demo 抽取公共组件,使…...

封装hutool工具生成JWT token
private static final String KEY "abcdef";/*** 生成token** param payload 可以存放用户的一些信息,不要存放敏感字段* return*/public static String createToken(Map<String, Object> payload) {//十分重要,不禁用发布到生产环境无…...

【手机】三星手机刷机解决SecSetupWizard已停止
三星手机恢复出厂设置之后,出现SecSetupWizard已停止的解决方案 零、问题 我手上有一部同学给的三星 GT-S6812I,这几天搞了张新卡,多余出的卡就放到这个手机上玩去了。因为是获取了root权限的(直接使用KingRoot就可以࿰…...

GDAL C++ API 学习之路 OGRGeometry 抽象曲线基类 OGRCurve
OGRCurve class "ogrsf_frmts.h" OGRCurve 是 OGR(OpenGIS Simple Features Reference Implementation)几何库中的一个基类,表示曲线几何对象。它是 OGRLineString 和 OGRCircularString 的抽象基类,用于表示曲…...

etcd底层支持的数据库有哪些
etcd底层的数据库可以更换。在当前版本的etcd中,它使用的是BoltDB作为默认的后端存储引擎。但是,etcd提供了接口允许您更换数据库后端,以便根据需要选择更合适的存储引擎。 以下是etcd支持的一些后端数据库选项: BoltDBÿ…...
linux设备驱动的poll与fasync
什么是fasync 在 Linux 驱动程序中,fasync 是一种机制,用于在异步事件发生时通知进程。它允许进程在等待设备事件时,不必像传统的轮询方式那样持续地查询设备状态。 具体来说,当进程调用 fcntl(fd, F_SETFL, O_ASYNC) 函数时&am…...
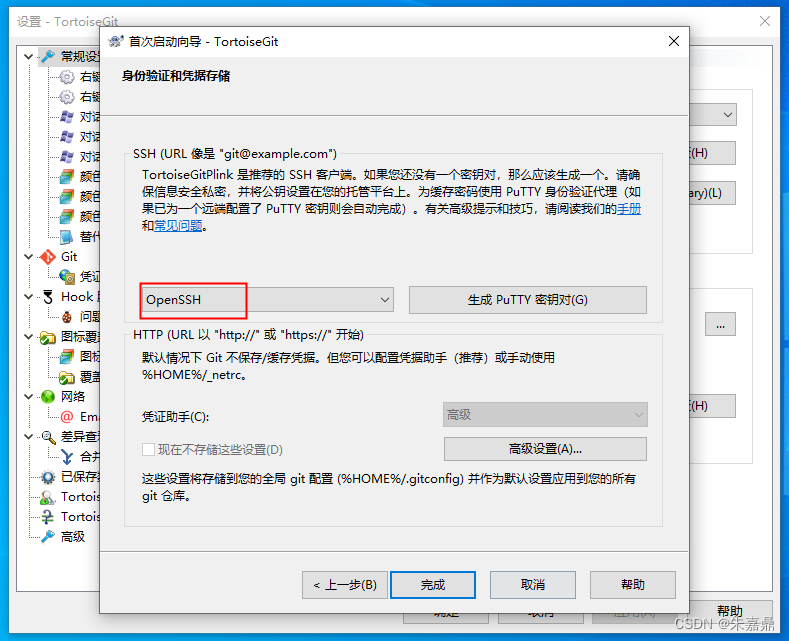
TortoiseGit安装与配置
注:在安装TortoiseGit之前我已经安装了git工具。 二、Git的诞生及环境配置_tortoisegit安装包_朱嘉鼎的博客-CSDN博客 1、TortoiseGit简介 TortoiseGit是基于TortoiseSVN的Git版本的Windows Shell界面。它是开源的,可以完全免费使用。 TortoiseGit 支持…...
)
Java代码打印空心菱形(小练习)
回看基础 利用Java代码打印一个空心菱形 //5. 打印空心菱形 import java.util.Scanner; public class MulForExercise01 {//编写一个 main 方法public static void main(String[] args) {Scanner myScanner new Scanner(System.in);System.out.println("请输入正三角的行…...

【性能优化】MySQL百万数据深度分页优化思路分析
业务场景 一般在项目开发中会有很多的统计数据需要进行上报分析,一般在分析过后会在后台展示出来给运营和产品进行分页查看,最常见的一种就是根据日期进行筛选。这种统计数据随着时间的推移数据量会慢慢的变大,达到百万、千万条数据只是时间问…...
交叉编译工具链的安装、配置、使用
一、交叉编译的概念 交叉编译是在一个平台上生成另一个平台上的可执行代码。 编译:一个平台上生成在该平台上的可执行文件。 例如:我们的Windows上面编写的C51代码,并编译成可执行的代码,如xx.hex.在C51上面运行。 我们在Ubunt…...
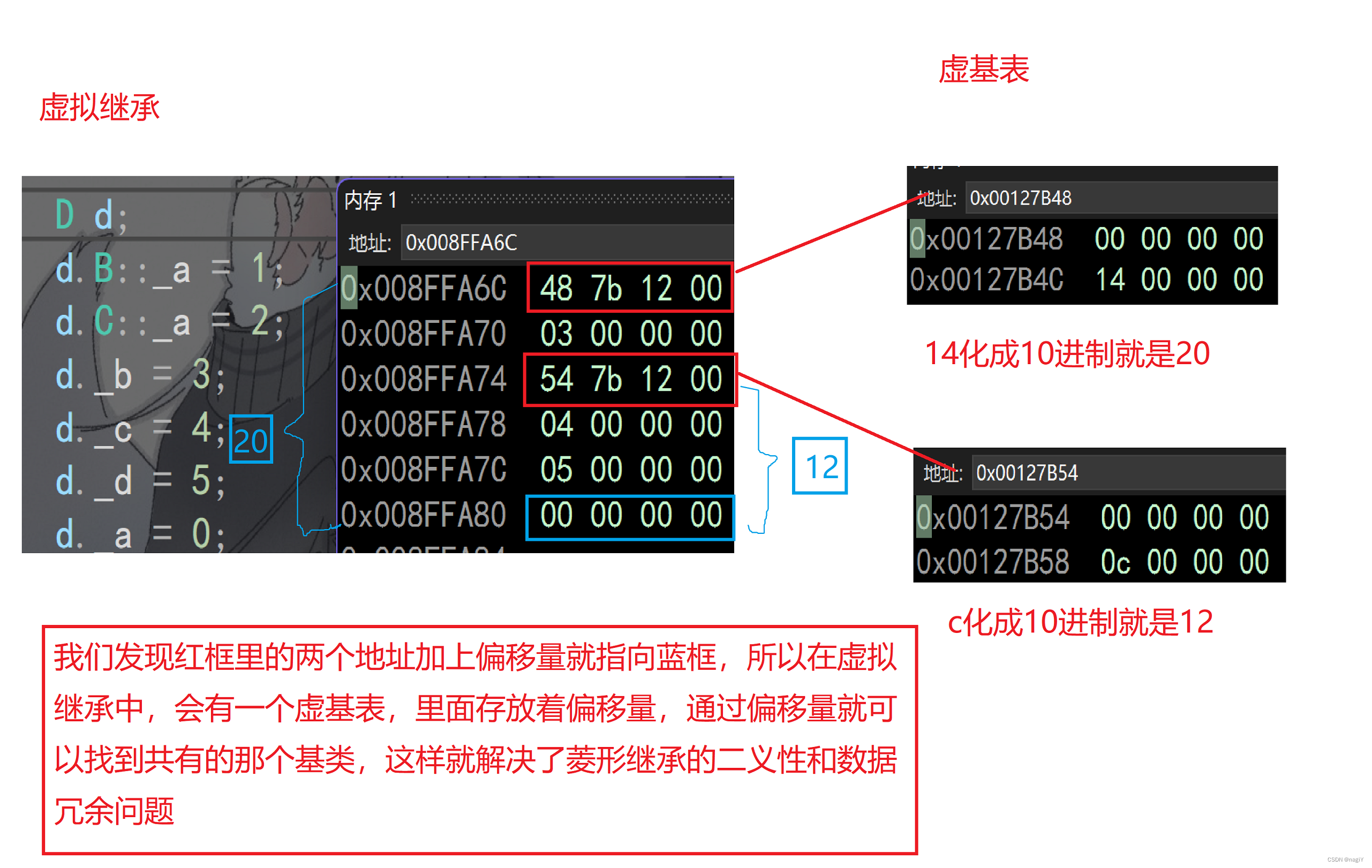
【C++ 进阶】继承
一.继承的定义格式 基类又叫父类,派生类又叫子类; 二.继承方式 继承方式分为三种: 1.public继承 2.protected继承 3.private继承 基类成员与继承方式的关系共有9种,见下表: 虽然说是有9种,但其实最常用的还…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
