C++笔记之迭代器失效问题处理
C++笔记之迭代器失效问题处理
code review!

参考博文:C++STL迭代器失效的几种情况总结
文章目录
- C++笔记之迭代器失效问题处理
- 一.使用返回新迭代器的插入和删除操作
- 二.对`std::vector` 来说,擦除(erase)元素会导致迭代器失效
一.使用返回新迭代器的插入和删除操作

二.对std::vector 来说,擦除(erase)元素会导致迭代器失效
对于 std::vector 来说,擦除(erase)元素会导致迭代器失效。具体而言,当从 std::vector 中删除元素时,原来指向被删除元素的迭代器就会失效,进而可能引起未定义行为。
处理迭代器失效的方法取决于具体的情况和需求。以下是一些处理迭代器失效的常见方法:
- 使用返回新迭代器的擦除操作:
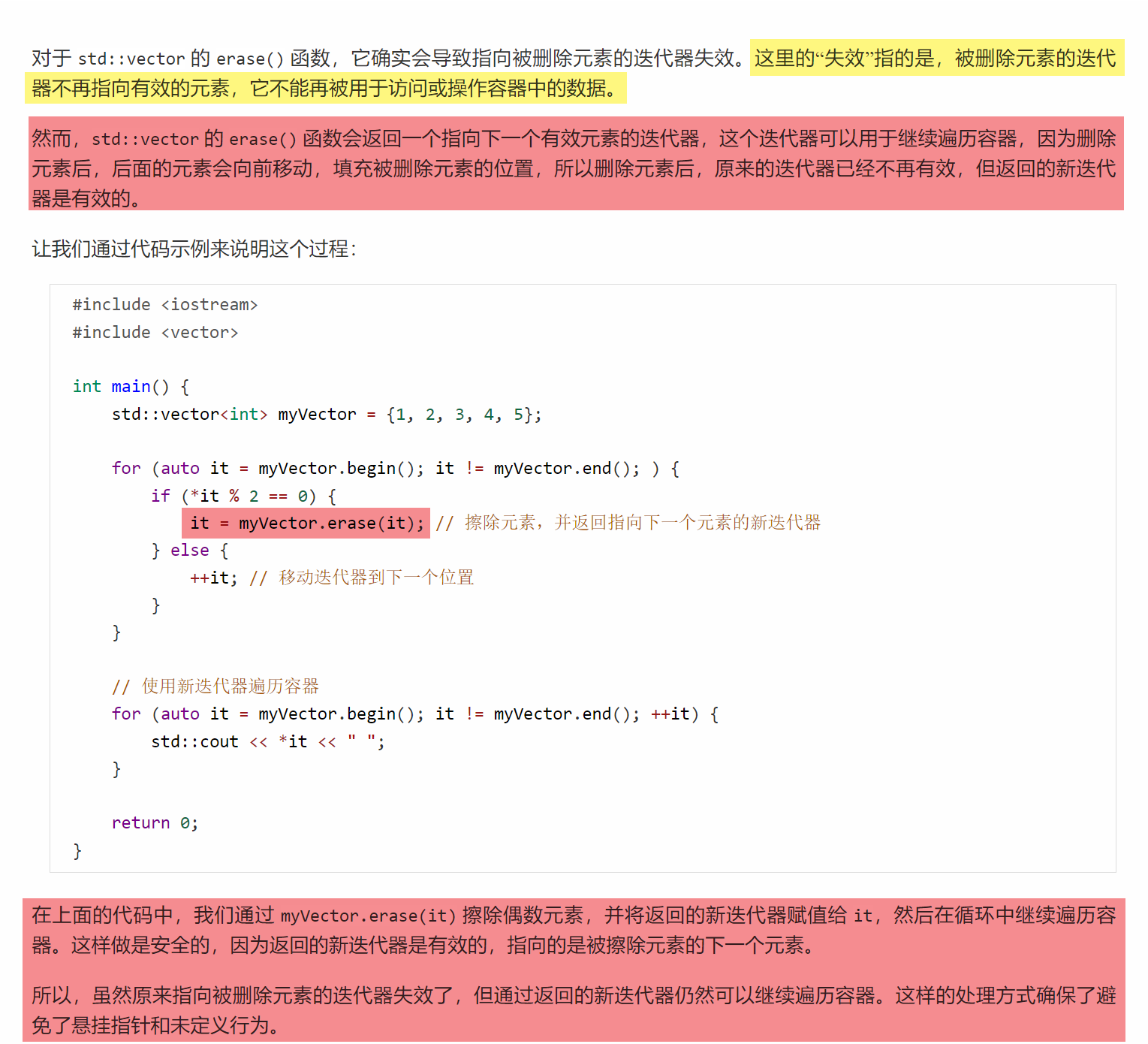
std::vector的erase()函数会返回一个指向下一个有效元素的迭代器。因此,在擦除元素后,可以使用返回的新迭代器继续遍历容器。
#include <iostream>
#include <vector>int main() {std::vector<int> myVector = {1, 2, 3, 4, 5};for (auto it = myVector.begin(); it != myVector.end(); ) {if (*it % 2 == 0) {it = myVector.erase(it); // 擦除元素,并返回指向下一个元素的新迭代器} else {++it; // 移动迭代器到下一个位置}}// 使用新迭代器遍历容器for (auto it = myVector.begin(); it != myVector.end(); ++it) {std::cout << *it << " ";}return 0;
}
- 使用标准算法:C++ 提供了一些标准算法,如
std::remove_if,用于在不失效迭代器的情况下移除满足条件的元素。
#include <iostream>
#include <vector>
#include <algorithm>int main() {std::vector<int> myVector = {1, 2, 3, 4, 5};myVector.erase(std::remove_if(myVector.begin(), myVector.end(), [](int n) {return n % 2 == 0;}), myVector.end());// 使用迭代器遍历容器for (auto it = myVector.begin(); it != myVector.end(); ++it) {std::cout << *it << " ";}return 0;
}
在此例中,我们使用 std::remove_if 来将满足条件的元素移到容器末尾,并返回一个指向新的逻辑尾部的迭代器,然后再使用 erase() 擦除这些元素。
总之,在删除 std::vector 的元素时,尽量使用返回新迭代器的擦除操作或者标准算法,以确保迭代器不会失效。在使用 erase() 函数后,使用返回的新迭代器来继续遍历容器。如果你需要在循环中擦除元素,请特别注意处理迭代器的有效性。
相关文章:

C++笔记之迭代器失效问题处理
C笔记之迭代器失效问题处理 code review! 参考博文:CSTL迭代器失效的几种情况总结 文章目录 C笔记之迭代器失效问题处理一.使用返回新迭代器的插入和删除操作二.对std::vector 来说,擦除(erase)元素会导致迭代器失效 一.使用返回…...

Tomcat的startup.bat文件出现闪退问题
对于双击Tomcat的startup.bat文件出现闪退问题,您提供的分析是正确的。主要原因是Tomcat需要Java Development Kit (JDK)的支持,而如果没有正确配置JAVA_HOME环境变量,Tomcat将无法找到JDK并启动,从而导致闪退。 以下是解决该问题…...

JAVA8-lambda表达式8:在设计模式-模板方法中的应用
传送门 JAVA8-lambda表达式1:什么是lambda表达式 JAVA8-lambda表达式2:常用的集合类api JAVA8-lambda表达式3:并行流,提升效率的利器? JAVA8-lambda表达式4:Optional用法 java8-lambda表达式5…...

React之组件间通信
React之组件间通信 组件通信: 简单讲就是组件之间的传值,包括state、函数等 1、父子组件通信 父组件给子组件传值 核心:1、自定义属性;2、props 父组件中: 自定义属性传值 import Header from /components/Headerconst Home ()…...
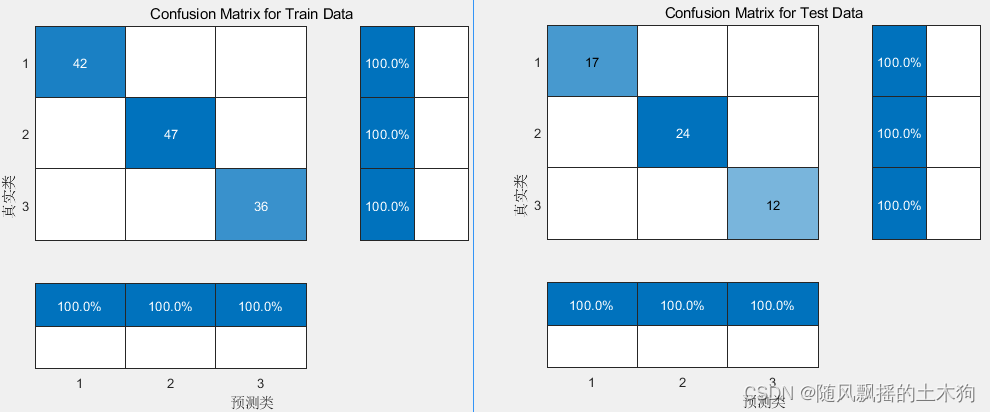
【MATLAB第58期】基于MATLAB的PCA-Kmeans、PCA-LVQ与BP神经网络分类预测模型对比
【MATLAB第58期】基于MATLAB的PCA-Kmeans、PCA-LVQ与BP神经网络分类预测模型对比 一、数据介绍 基于UCI葡萄酒数据集进行葡萄酒分类及产地预测 共包含178组样本数据,来源于三个葡萄酒产地,每组数据包含产地标签及13种化学元素含量,即已知类…...
CF1833 A-E
A题 题目链接:https://codeforces.com/problemset/problem/1833/A 基本思路:for循环遍历字符串s,依次截取字符串s的子串str,并保存到集合中,最后输出集合内元素的数目即可 AC代码: #include <iostrea…...

【深度学习】【Image Inpainting】Generative Image Inpainting with Contextual Attention
Generative Image Inpainting with Contextual Attention DeepFillv1 (CVPR’2018) 论文:https://arxiv.org/abs/1801.07892 论文代码:https://github.com/JiahuiYu/generative_inpainting 论文摘录 文章目录 效果一览摘要介绍论文贡献相关工作Image…...
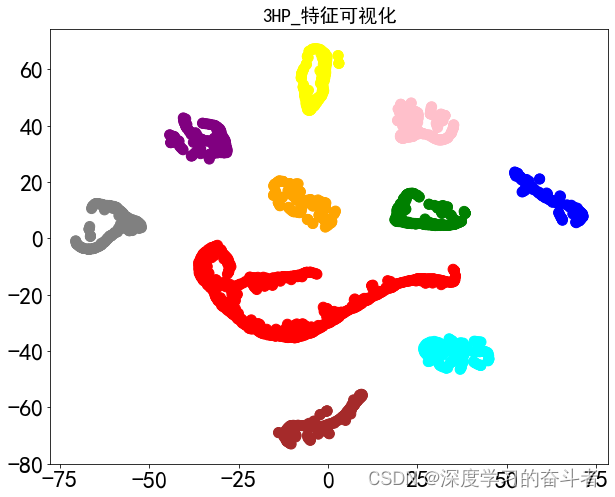
二维深度卷积网络模型下的轴承故障诊断
1.数据集 使用凯斯西储大学轴承数据集,一共有4种负载下采集的数据,每种负载下有10种 故障状态:三种不同尺寸下的内圈故障、三种不同尺寸下的外圈故障、三种不同尺寸下的滚动体故障和一种正常状态 2.模型(二维CNN) 使…...

redis突然变慢问题定位
CPU 相关:使用复杂度过高命令、O(N)的这个N,数据的持久化,都与耗费过多的 CPU 资源有关 内存相关:bigkey 内存的申请和释放、数据过期、数据淘汰、碎片整理、内存大页、内存写时复制都与内存息息相关 磁盘…...
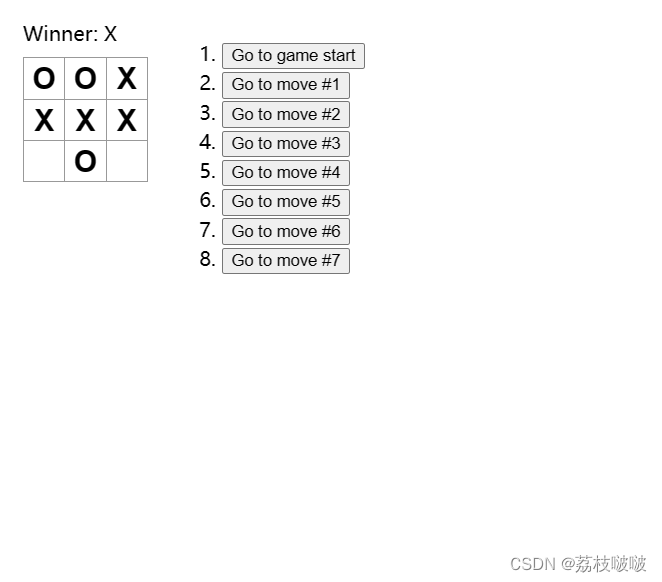
React井字棋游戏官方示例
在本篇技术博客中,我们将介绍一个React官方示例:井字棋游戏。我们将逐步讲解代码实现,包括游戏的组件结构、状态管理、胜者判定以及历史记录功能。让我们一起开始吧! 项目概览 在这个井字棋游戏中,我们有以下组件&am…...

七大经典比较排序算法
1. 插入排序 (⭐️⭐️) 🌟 思想: 直接插入排序是一种简单的插入排序法,思想是是把待排序的数据按照下标从小到大,依次插入到一个已经排好的序列中,直至全部插入,得到一个新的有序序列。例如:…...
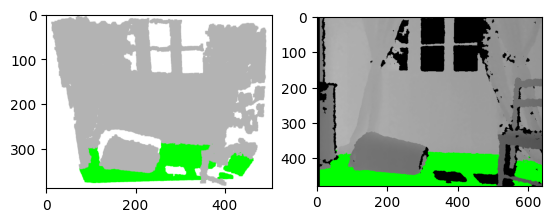
【点云处理教程】03使用 Python 实现地面检测
一、说明 这是我的“点云处理”教程的第3篇文章。“点云处理”教程对初学者友好,我们将在其中简单地介绍从数据准备到数据分割和分类的点云处理管道。 在上一教程中,我们在不使用 Open3D 库的情况下从深度数据计算点云。在本教程中,我们将首先…...
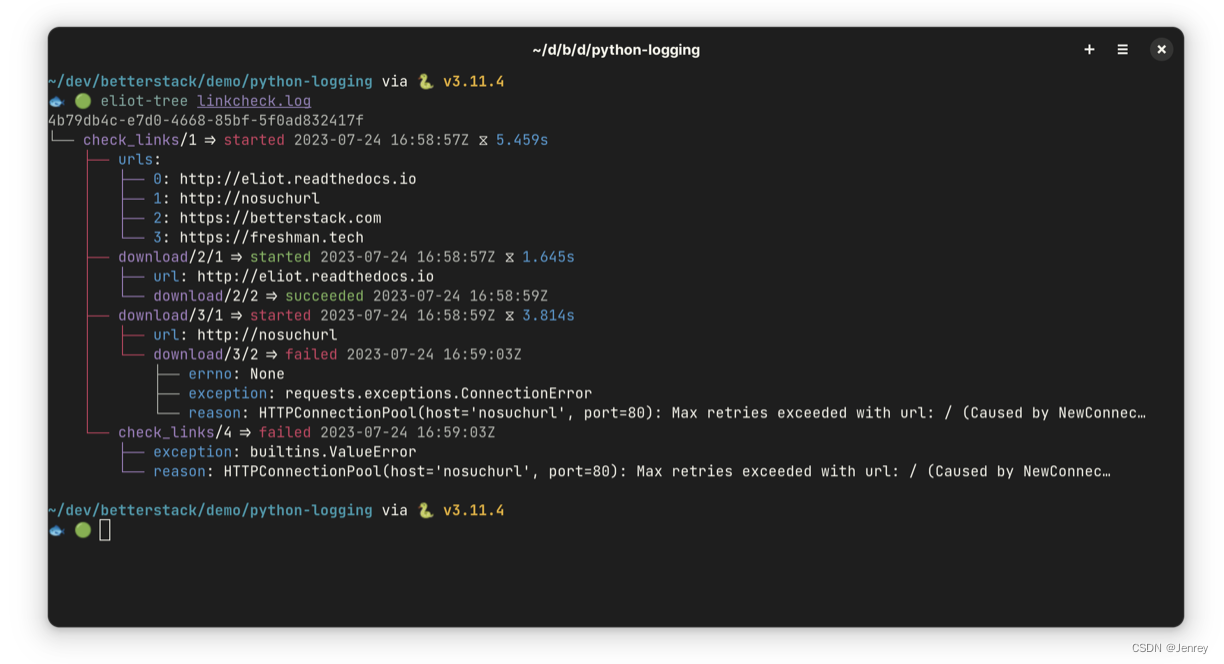
Python 日志记录:6大日志记录库的比较
Python 日志记录:6大日志记录库的比较 文章目录 Python 日志记录:6大日志记录库的比较前言一些日志框架建议1. logging - 内置的标准日志模块默认日志记录器自定义日志记录器生成结构化日志 2. Loguru - 最流行的Python第三方日志框架默认日志记录器自定…...

最近遇到一些问题的解决方案
最近遇到一些问题的解决方案 SpringBoot前后端分离参数传递方式总结Java8版本特性讲解idea使用git更新代码 : update project removeAll引发得java.lang.UnsupportedOperationException异常Java的split()函数用多个不同符号分割 Aspect注解切面demo 抽取公共组件,使…...

封装hutool工具生成JWT token
private static final String KEY "abcdef";/*** 生成token** param payload 可以存放用户的一些信息,不要存放敏感字段* return*/public static String createToken(Map<String, Object> payload) {//十分重要,不禁用发布到生产环境无…...

【手机】三星手机刷机解决SecSetupWizard已停止
三星手机恢复出厂设置之后,出现SecSetupWizard已停止的解决方案 零、问题 我手上有一部同学给的三星 GT-S6812I,这几天搞了张新卡,多余出的卡就放到这个手机上玩去了。因为是获取了root权限的(直接使用KingRoot就可以࿰…...

GDAL C++ API 学习之路 OGRGeometry 抽象曲线基类 OGRCurve
OGRCurve class "ogrsf_frmts.h" OGRCurve 是 OGR(OpenGIS Simple Features Reference Implementation)几何库中的一个基类,表示曲线几何对象。它是 OGRLineString 和 OGRCircularString 的抽象基类,用于表示曲…...

etcd底层支持的数据库有哪些
etcd底层的数据库可以更换。在当前版本的etcd中,它使用的是BoltDB作为默认的后端存储引擎。但是,etcd提供了接口允许您更换数据库后端,以便根据需要选择更合适的存储引擎。 以下是etcd支持的一些后端数据库选项: BoltDBÿ…...
linux设备驱动的poll与fasync
什么是fasync 在 Linux 驱动程序中,fasync 是一种机制,用于在异步事件发生时通知进程。它允许进程在等待设备事件时,不必像传统的轮询方式那样持续地查询设备状态。 具体来说,当进程调用 fcntl(fd, F_SETFL, O_ASYNC) 函数时&am…...
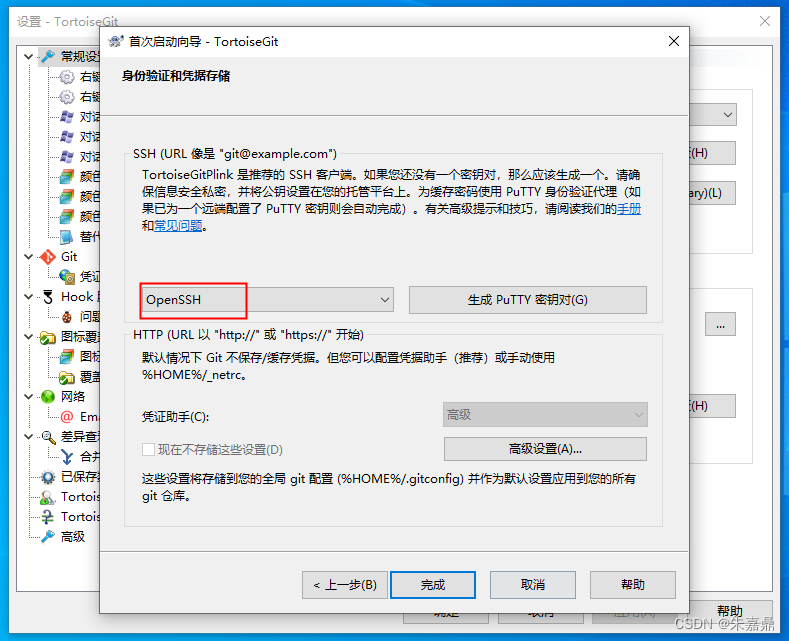
TortoiseGit安装与配置
注:在安装TortoiseGit之前我已经安装了git工具。 二、Git的诞生及环境配置_tortoisegit安装包_朱嘉鼎的博客-CSDN博客 1、TortoiseGit简介 TortoiseGit是基于TortoiseSVN的Git版本的Windows Shell界面。它是开源的,可以完全免费使用。 TortoiseGit 支持…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
