神经网络简单介绍
人工神经网络(artififial neural network) 简称神经网络,它是一种模仿生物神经网络结构和功能的非线性数学模型。
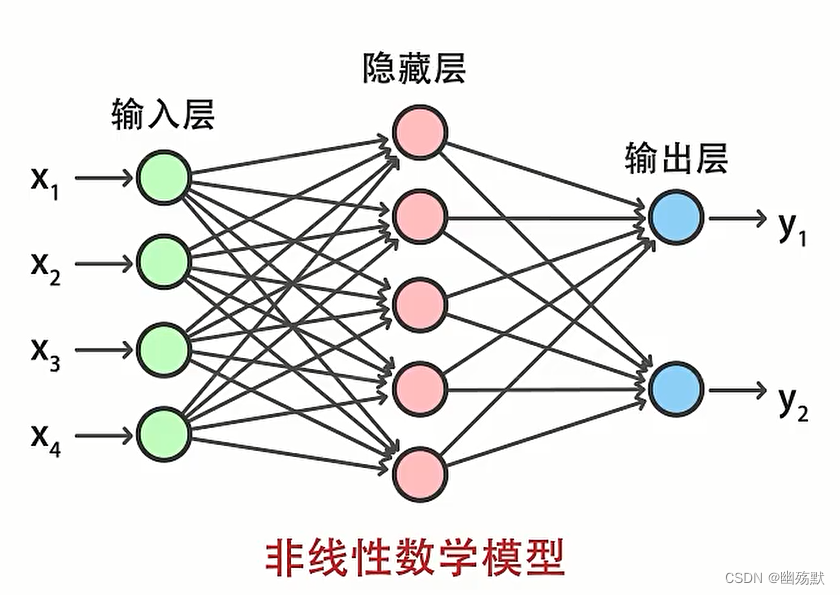
神经网络通过输入层接受原始特征信息,再通过隐藏层进行特征信息的加工和提取,最后通过输出层输出结果。
根据需要神经网络可以包含多层隐藏层。
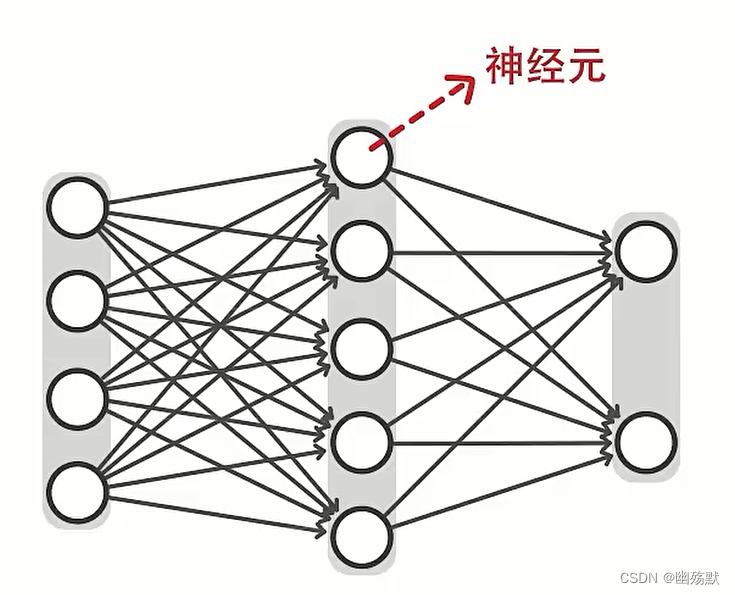
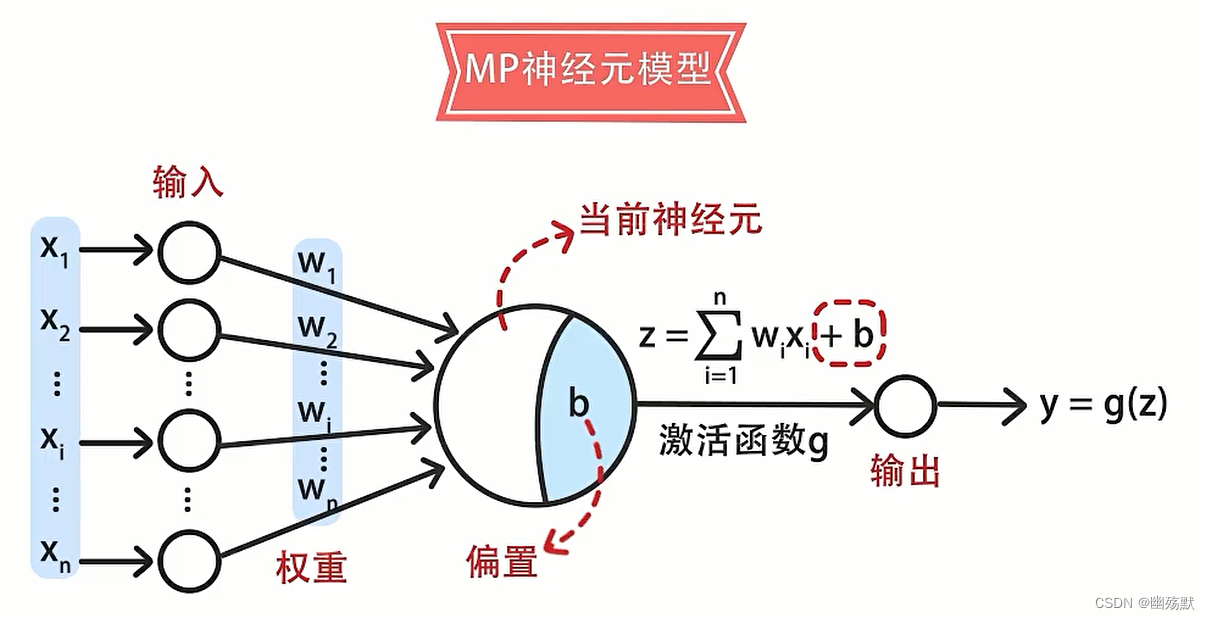
激活函数它用于将输入数据映射到输出端,通过激活函数将非线性特征引入神经元。从而得到神经网络可以任意逼近任何非线性函数。
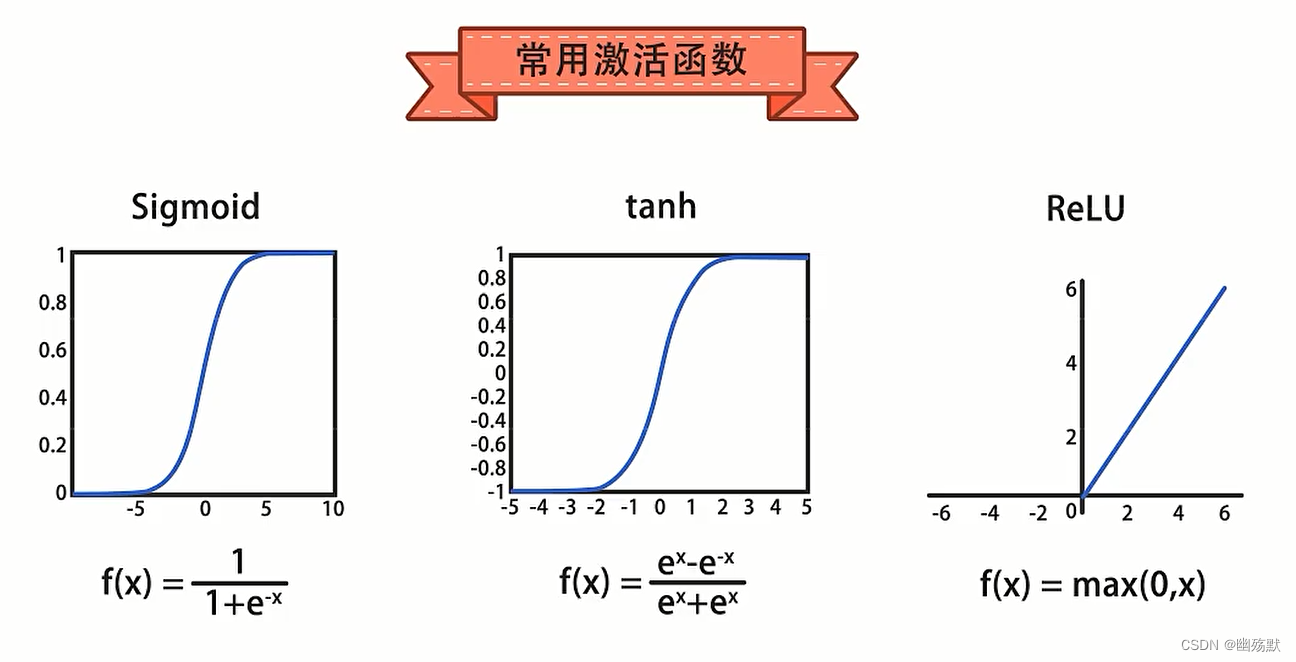

Sigmoid函数将值压缩到[0-1]之间。tanh函数将值压缩到[-1,1]之间。
激活函数在神经网络中起着非常重要的作用。它们是一类非线性函数,被应用于神经元或人工神经元的输出,用于引入非线性特性。以下是激活函数的几个关键作用:
- 引入非线性:线性函数的组合仍然只能得到线性函数,而激活函数的非线性特性能够使神经网络具备处理非线性关系的能力。这对于解决复杂的问题非常关键,因为许多自然现象和人类行为往往都是非线性的。
改善模型的表达能力:通过引入非线性变换,激活函数能够帮助神经网络更好地学习和表示非线性函数。这使得神经网络能够逼近非线性映射,从而提高模型的表达能力。 - 解决梯度消失问题:在深层神经网络中,反向传播时梯度可能会变得非常小,从而导致梯度消失问题。一些激活函数,如ReLU(Rectified Linear Unit),能够缓解这个问题,因为它们的导数在一定范围内保持恒定。这有助于梯度在网络中传播得更远,使得网络能够更好地学习。
- 控制神经元的激活状态:激活函数的输出可以被看作是神经元的激活状态。通过调整激活函数的参数和形状,我们可以控制神经元是否激活以及激活的程度。这对于控制神经网络的整体行为和输出非常重要。
- 常见的激活函数包括Sigmoid函数、ReLU函数、Leaky ReLU函数、Tanh函数等。选择适合的激活函数取决于具体的任务和数据特点,在实际应用中需要根据实验和经验进行选择。
相关文章:

神经网络简单介绍
人工神经网络(artififial neural network) 简称神经网络,它是一种模仿生物神经网络结构和功能的非线性数学模型。 神经网络通过输入层接受原始特征信息,再通过隐藏层进行特征信息的加工和提取,最后通过输出层输出结果。 根据需要神经网络可以…...
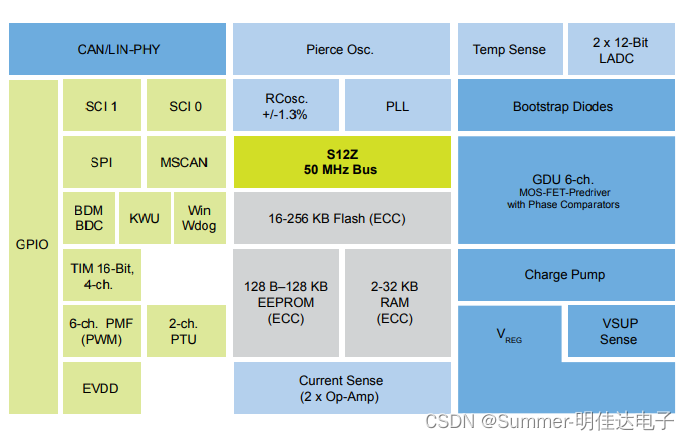
16位S912ZVML32F3MKH、S912ZVML31F1WKF、S912ZVML31F1MKH混合信号MCU,适用于汽车和工业电机控制应用。
S12 MagniV微控制器是易于使用且高度集成的混合信号MCU,非常适合用于汽车和工业应用。S12 MagniV MCU提供单芯片解决方案,是基于成熟的S12技术的完整系统级封装 (SiP) 解决方案,在整个产品组合内软件和工具都兼容。 S12 MagniV系统级封装 (S…...

力扣 509. 斐波那契数
题目来源:https://leetcode.cn/problems/fibonacci-number/description/ C题解1:根据题意,直接用递归函数。 class Solution { public:int fib(int n) {if(n 0) return 0;else if(n 1) return 1;else return(fib(n-1) fib(n-2));} }; C题…...

使用 DolphinDB TopN 函数探索高效的Alpha因子
DolphinDB 已经有非常多的窗口计算函数,例如 m 系列的滑动窗口计算,cum 系列累计窗口计算,tm 系列的的时间窗口滑动计算。但是所有这类函数都是对窗口内的所有记录进行指标计算,难免包含很多噪音。 DolphinDB 的金融领域用户反馈…...

超聚变和厦门大学助力兴业银行构建智慧金融隐私计算平台,助力信用卡业务精准营销...
兴业银行与超聚变数字技术有限公司、厦门大学携手,发挥产学研用一体化整体优势联合建设,厦门大学提供先进的算法模型及科研能力,超聚变提供产品解决方案及工程能力,兴业银行提供金融实践能力,三方发挥各自领域优势&…...

docker 的compose安装
1. Docker Compose 环境安装 Docker Compose 是 Docker 的独立产品,因此需要安装 Docker 之后在单独安装 Docker Compose docker compose 实现单机容器集群编排管理(使用一个模板文件定义多个应用容器的启动参数和依赖关系,并使用docker co…...

JavaScript---事件对象event
获取事件对象: 事件对象:是个对象,这个对象里有事件触发时的相关信息,在事件绑定的回调函数的第一个参数就是事件对象,一般命名为event、ev、e eg: 元素.addEventListener(click,function (e){}) 部分常用属性&…...

Day 15 C++对象模型和this指针
目录 C对象模型 类内的成员变量和成员函数分开存储 总结 this指针 概念 示例 用途 当形参和成员变量同名时 在非静态成员函数中,如果希望返回对象本身 例子 空指针访问成员函数 示例 const修饰成员函数 常函数(const member function&…...

HarmonyOS/OpenHarmony元服务开发-卡片生命周期管理
创建ArkTS卡片,需实现FormExtensionAbility生命周期接口。 1.在EntryFormAbility.ts中,导入相关模块。 import formInfo from ohos.app.form.formInfo; import formBindingData from ohos.app.form.formBindingData; import FormExtensionAbility from …...

软件工程01
软件工程原则: 开闭原则: open closed principle : 对扩展开放,对修改关闭,,,只让扩展,不让修改,用新增的类去替代修改的类 扩展之后,代码不用改变ÿ…...
UML/SysML建模工具更新(2023.7)(1-5)有国产工具
DDD领域驱动设计批评文集 欢迎加入“软件方法建模师”群 《软件方法》各章合集 最近一段时间更新的工具有: 工具最新版本:Visual Paradigm 17.1 更新时间:2023年7月11日 工具简介 很用心的建模工具。支持编写用例规约。支持文本分析和C…...

Mac plist文件
macOS、iOS、iPadOS的应用程序都可能会有plist配置文件,他是苹果系列操作系统特有的配置文件。 plist的本质是个xml格式的文本文件,英文全称是property list,文件后缀使用.plist。 对于普通用户来说,基本不用管plist文件是什么&…...
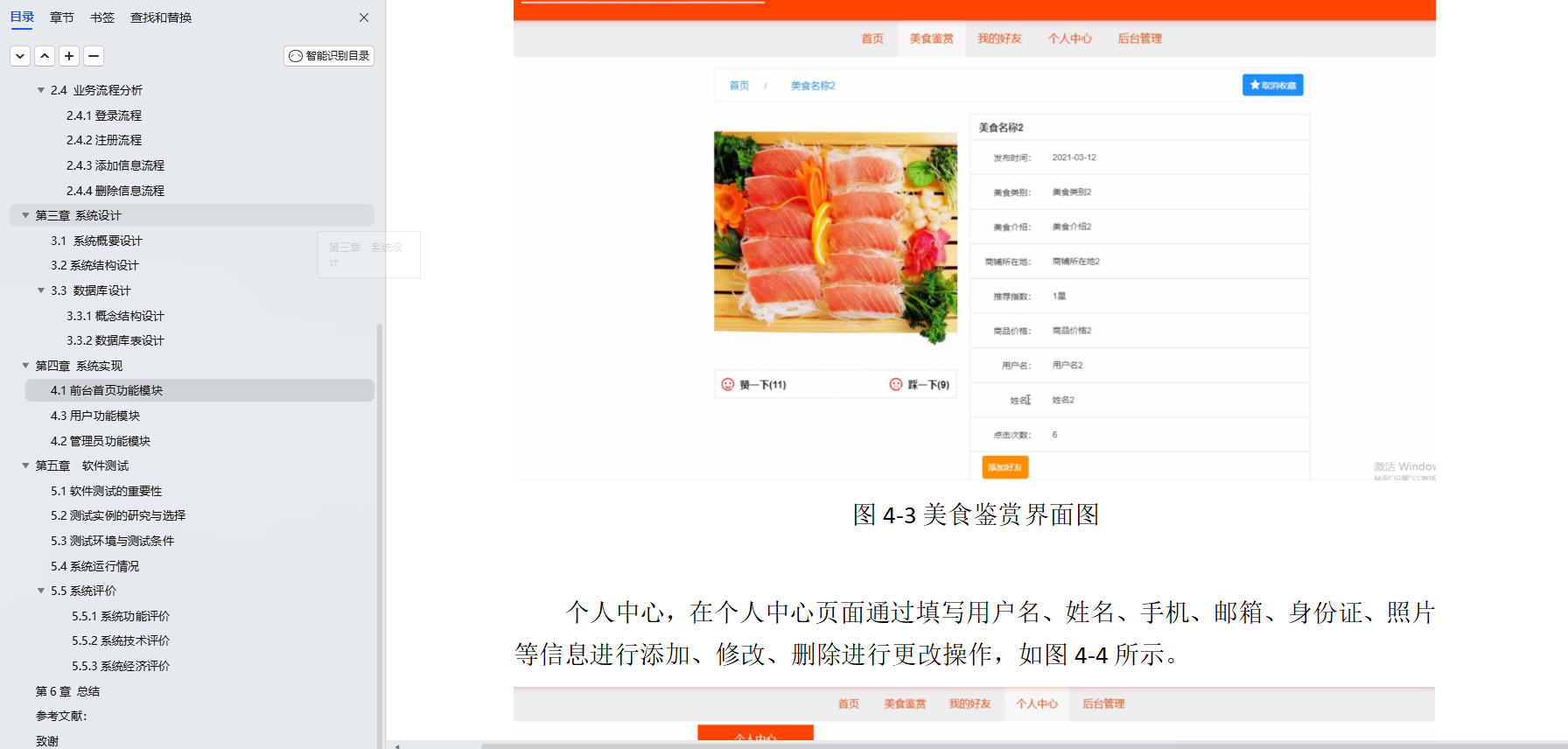
基于Java+SpringBoot+vue前后端分离校园周边美食探索分享平台设计实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

【openwrt】package介绍
openwrt package介绍 OpenWrt 构建系统主要围绕package的概念展开。不管是什么软件,几乎都对应一个package。 这几乎适用于系统中的所有内容:HOST工具、交叉编译工具链、Linux 内核、内核mod、根文件系统和上层的应用软件。 一个 OpenWrt package本质上…...

vue 封装一个鼠标拖动选择时间段功能
<template><div class"timeRange"><div class"calendar"><table><thead><tr><th rowspan"6" class"weekRow"><b>周/时间</b></th><th colspan"24"><…...

ubuntu22.0安装Barrier局域网共享鼠标键盘
ubuntu22.0安装Barrier局域网共享鼠标键盘 参考网站安装步骤客户端一直开启中解决 参考网站 https://idroot.us/install-barrier-ubuntu-22-04/ 安装步骤 sudo apt update sudo apt upgrade sudo apt install wget apt-transport-https gnupg2 software-properties-common s…...

ffmpeg常用功能博客导航
FFmpeg 是一个处理视频和音频内容的开源工具库,可以实现编码、解码、转码、流媒体和后处理等服务。 推荐博客: 常见命令和使用案例 用ffmpeg转mov为mp4格式 FFmpeg 常用命令 FFmpeg 常用命令编辑音/视频(转换格式、压缩、裁剪、截图、切分合…...

shopee,lazada,etsy店群如何高效安全的管理
对于电商卖家来说,要经营多个店铺,管理多个账号是非常常见的操作。为了避免账号关联被平台识别出来,需要使用防关联的浏览器来进行操作 1、支持多平台 支持同时管理多个电商平台店铺,Shopee、Lazada、etsy、poshmark、vinted等&…...
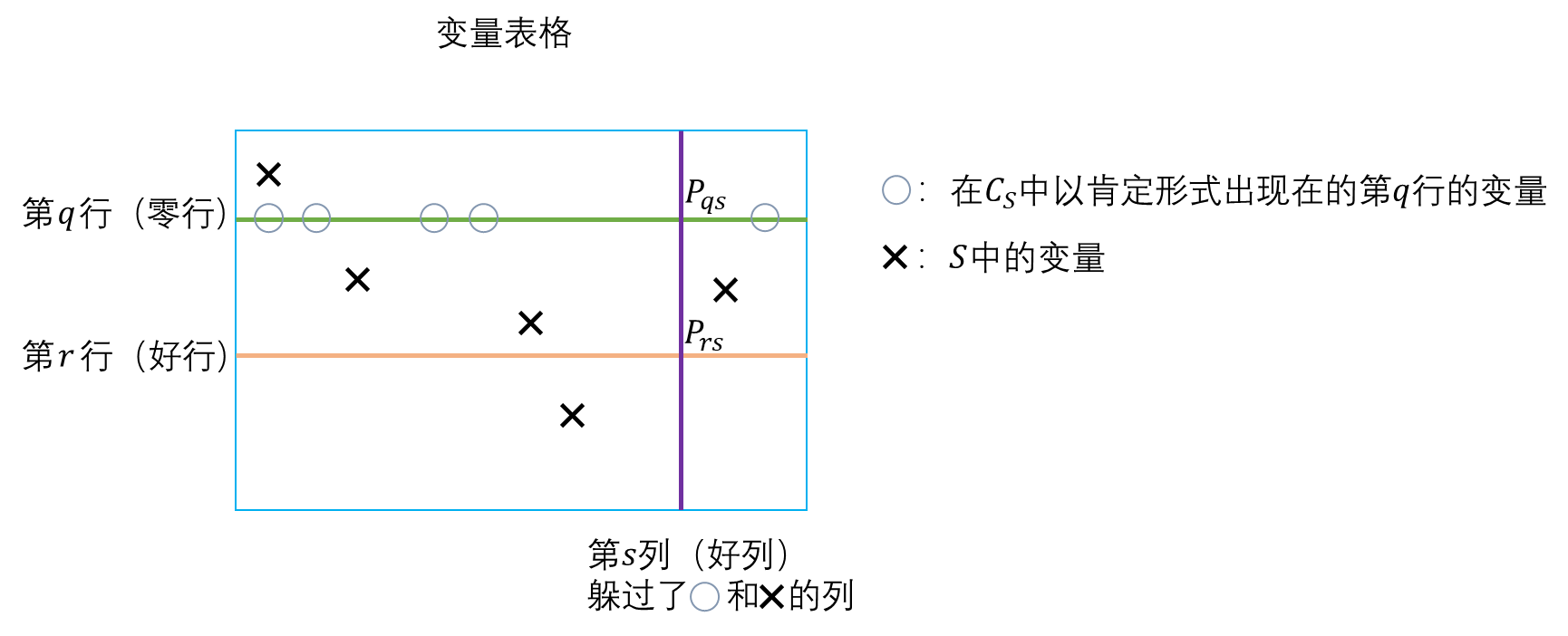
【计算复杂性理论】证明复杂性(八):命题鸽巢原理(Propositional Pigeonhole Principle)的指数级归结下界
往期文章: 【计算复杂性理论】证明复杂性(Proof Complexity)(一):简介 【计算复杂性理论】证明复杂性(二):归结(Resolution)与扩展归结ÿ…...
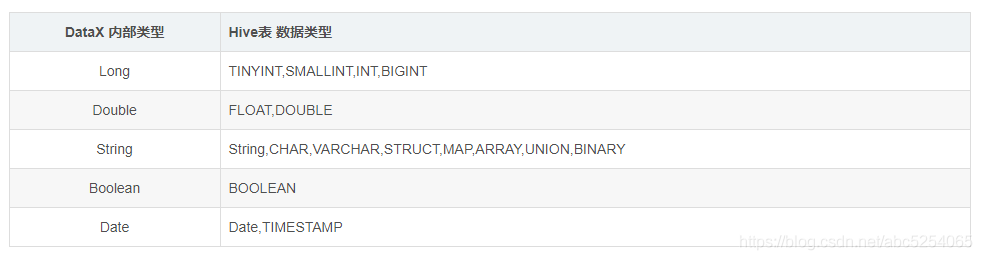
使用DataX实现mysql与hive数据互相导入导出
一、概论 1.1 什么是DataX DataX 是阿里巴巴开源的一个异构数据源离线同步工具,致力于实现包括关系型数据库(MySQL、Oracle 等)、HDFS、Hive、ODPS、HBase、FTP 等各种异构数据源之间稳定高效的数据同步功能。 1.2 DataX 的设计 为了解决异构数据源同步问题…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
