秋招算法备战第31天 | 贪心算法理论基础、455.分发饼干、376. 摆动序列、53. 最大子序和
贪心算法理论基础
- 贪心算法并没有固定的套路,唯一的难点就是如何通过局部最优,推出整体最优。
- 如何验证可不可以用贪心算法呢?最好用的策略就是举反例,如果想不到反例,那么就试一试贪心吧。
- 刷题或者面试的时候,手动模拟一下感觉可以局部最优推出整体最优,而且想不到反例,那么就试一试贪心。
贪心算法一般分为如下四步:
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步去思考,真是有点“鸡肋”。做题的时候,只要想清楚 局部最优 是什么,如果推导出全局最优,其实就够了。
455. 分发饼干 - 力扣(LeetCode)
这是一个经典的贪心算法问题,策略是优先满足胃口小的孩子。具体操作就是先将孩子的胃口数组和饼干尺寸数组排序,然后从小到大匹配。如果当前饼干可以满足当前孩子,就把饼干给孩子,然后移动到下一个孩子和下一个饼干;如果当前饼干无法满足当前孩子,就放弃当前饼干,移动到下一个饼干。
这种算法的理论支持是,如果当前饼干无法满足当前孩子,那么它也无法满足胃口更大的孩子,因此应该放弃。如果可以满足当前孩子,就应该先满足他,因为下一个饼干不一定能满足下一个孩子,但是下一个饼干可能会满足当前孩子或者胃口更大的孩子。
Python实现代码如下:
def findContentChildren(g, s):g.sort()s.sort()child_i = cookie_j = 0while child_i < len(g) and cookie_j < len(s):if s[cookie_j] >= g[child_i]:child_i += 1cookie_j += 1return child_i
在这段代码中,g代表孩子的胃口数组,s代表饼干的尺寸数组。函数返回的是能够满足的孩子数量。数组g和s都先进行了排序,然后用两个指针child_i和cookie_j分别遍历孩子和饼干。如果当前饼干能满足当前孩子,就将饼干给孩子,然后考虑下一个孩子和下一个饼干;否则放弃当前饼干,考虑下一个饼干。这样一直进行,直到没有孩子或者饼干为止。最后返回满足的孩子数量child_i,即为结果。
376. 摆动序列 - 力扣(LeetCode)
贪心算法
在这个问题中,贪心算法的策略是我们始终尽可能地使序列保持摆动。换句话说,我们总是优先考虑改变趋势,即如果当前是上升的,我们就寻找下一个下降的点,反之亦然。
这个问题实际上是找出数组中的所有"转折点"。一个"转折点"是指该点两侧的差值与该点和其前一点的差值异号。也就是说,如果该点比前一点大,那么它应该比后一点小;反之亦然。
这种策略可以通过一次遍历完成,时间复杂度是O(n)。
Python实现代码如下:
def wiggleMaxLength(nums):n = len(nums)if n < 2:return nprevdiff = nums[1] - nums[0]count = 2 if prevdiff != 0 else 1for i in range(2, n):diff = nums[i] - nums[i - 1]if (diff > 0 and prevdiff <= 0) or (diff < 0 and prevdiff >= 0):count += 1prevdiff = diffreturn count
在这段代码中,nums代表给定的整数数组。函数返回的是最长摆动子序列的长度。首先计算前两个数字的差值prevdiff,然后从第三个数字开始,如果当前数字与前一个数字的差值diff和prevdiff异号,说明当前数字是一个转折点,摆动序列长度增加1,然后更新prevdiff为当前的差值。最后返回摆动序列长度count,即为结果。
这个算法的时间复杂度是O(n),空间复杂度是O(1),满足题目的要求。
动态规划
这是一道典型的动态规划问题,我们需要找到数组中的最长摆动子序列的长度。
我们可以维护两个动态规划数组 up 和 down,其中 up[i] 表示在到达数组的第 i 个位置时,最后一次摆动是上升的最长子序列长度,down[i] 表示在到达数组的第 i 个位置时,最后一次摆动是下降的最长子序列长度。
状态转移方程为:
- 如果
nums[i] > nums[i - 1],那么我们可以在以i - 1结尾的下降子序列后面接一个nums[i],形成一个更长的摆动序列,所以有up[i] = down[i - 1] + 1,down[i] = down[i - 1]; - 如果
nums[i] < nums[i - 1],那么我们可以在以i - 1结尾的上升子序列后面接一个nums[i],形成一个更长的摆动序列,所以有down[i] = up[i - 1] + 1,up[i] = up[i - 1]; - 如果
nums[i] == nums[i - 1],那么我们无法在子序列后面接一个nums[i]形成一个更长的摆动序列,所以有up[i] = up[i - 1],down[i] = down[i - 1]。
最后的答案就是 up[n - 1] 和 down[n - 1] 的最大值。
Python 代码如下:
def wiggleMaxLength(nums):n = len(nums)if n < 2:return nup = [0] * ndown = [0] * nup[0] = down[0] = 1for i in range(1, n):if nums[i] > nums[i - 1]:up[i] = max(up[i - 1], down[i - 1] + 1)down[i] = down[i - 1]elif nums[i] < nums[i - 1]:up[i] = up[i - 1]down[i] = max(up[i - 1] + 1, down[i - 1])else:up[i] = up[i - 1]down[i] = down[i - 1]return max(up[-1], down[-1])
这段代码中,nums 代表给定的整数数组。函数返回的是最长摆动子序列的长度。数组 up 和 down 存储了以每个位置结尾的最长上升和下降摆动子序列的长度。然后通过状态转移方程更新 up 和 down,最后返回 up 和 down 的最大值,即为最长摆动子序列的长度。
这个算法的时间复杂度是 O(n),空间复杂度是 O(n),满足题目的要求。
53. 最大子数组和 - 力扣(LeetCode)
贪心算法
贪心算法的思路是:遍历数组,并在每个步骤中维护当前的子数组和以及到目前为止找到的最大子数组和。如果当前子数组和变为负数,则在下一个元素处开始新的子数组。
Python实现代码如下:
def maxSubArray(nums):current_sum = max_sum = nums[0]for num in nums[1:]:current_sum = max(num, current_sum + num)max_sum = max(max_sum, current_sum)return max_sum
动态规划
动态规划的思路稍微复杂一些。设dp[i]表示以第i个元素结尾的最大子数组和,那么dp[i]可以由dp[i-1]和nums[i]决定。如果dp[i-1]大于0,dp[i]就等于dp[i-1]加上nums[i],否则等于nums[i]。我们要求的结果就是dp数组中的最大值。
Python实现代码如下:
def maxSubArray(nums):dp = [0] * len(nums)dp[0] = nums[0]for i in range(1, len(nums)):dp[i] = max(dp[i-1] + nums[i], nums[i])return max(dp)
两种算法的时间复杂度都是O(n),空间复杂度上,贪心算法是O(1),动态规划是O(n),如果将动态规划的解法优化一下,可以降低到O(1),因为dp[i]只依赖于dp[i-1]。
优化后的动态规划解法:
def maxSubArray(nums):max_sum = curr_sum = nums[0]for num in nums[1:]:curr_sum = max(curr_sum + num, num)max_sum = max(max_sum, curr_sum)return max_sum
这个解法与贪心算法看起来非常相似,但它们的思考方式是不同的。贪心算法是在每一步都采取局部最优解,而动态规划则是在每一步都根据前一步的结果做出决策。
总结
贪心算法是在每一步都采取局部最优解,而动态规划则是在每一步都根据前一步的结果做出决策。
相关文章:

秋招算法备战第31天 | 贪心算法理论基础、455.分发饼干、376. 摆动序列、53. 最大子序和
贪心算法理论基础 贪心算法并没有固定的套路,唯一的难点就是如何通过局部最优,推出整体最优。如何验证可不可以用贪心算法呢?最好用的策略就是举反例,如果想不到反例,那么就试一试贪心吧。刷题或者面试的时候…...
页面生成图片或PDF node-egg
没有特别的幸运,那么就特别的努力!!! 中间件:页面生成图片 node-egg 涉及到技术node egg Puppeteer 解决文书智能生成多样化先看效果环境准备初始化项目 目录结构核心代码 完整代码https://gitee.com/hammer1010_ad…...

go常用知识点
go env -w GO111MODULEon go env -w GOPROXYhttps://goproxy.cn,direct 打包一个目录下的多个包时 go build ./… go install ./… 测试时,命令行:go test . //目录下所有单元测试都会执行 go test -v 目录 //测试覆盖率 go test -cover //使用cove…...
)
ComPDFKit PDF SDK(支持Web、Android、IOS、Windows、Server、API、跨平台)
1. SDK、API是什么? SDK是软件开发工具包的缩写,指的是一组用于开发软件应用的工具、库和文档。SDK包含一系列的函数、类和方法,开发人员可以使用这些工具和资源来开发、测试和部署应用程序。SDK可以提供各种功能和技术支持,如图…...

使用maven容器打包java项目
docker run --rm -v /path/to/your/microservice:/app -w /app maven:latest mvn clean package 解释一下上面的命令: docker run:运行Docker容器。--rm:在容器运行结束后自动删除容器,避免堆积未使用的容器。-v /path/to/you…...
超前端相关的学习网站和一些靠谱的小工具
CSS相关 1. CSS Battle - 在线比拼 CSS https://cssbattle.dev 在线比拼 CSS ,一个挺有趣的竞争性游戏,一共有12个级别,需要你用 HTML和 CSS 100%还原它给出的页面,然后再尽量减少代码,你也可以查看全球的排行榜&am…...

uniapp跳转到外部链接
// 一、先配置页面 {"path": "pages/webview/webview","style": {"navigationBarTitleText": ""} } // 二、编写页面 <template><web-view :src"src" /> </template><script> export def…...
初识DBT以及搭建第一个DBT工程
DBT是什么: 按照官方的说法,DBT 是一个数据转换流编排工具。个人理解就是,DBT是帮你编排SQL用的,你可以按照DBT的结构,构建好一个SQL的pipeline,然后让DBT帮你执行这个pipeline。我这里说的SQL pipeline的意…...
Python基于PyTorch实现卷积神经网络回归模型(CNN回归算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 卷积神经网络,简称为卷积网络,与普通神经网络的区别是它的卷积层内的神经元只覆…...
集合-Nim游戏)
(AcWing)集合-Nim游戏
给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。 现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合 S,最后无法进行操作的人视为失败。 问如果两人都采用最优策略,先…...

ConcurrentHashMap源码详解
本文已收录于专栏 《Java》 目录 概念说明数据结构线程安全HashMap示例运行结果ConcurrentHashMap示例运行结果 涉及技术Synchronized概念特性 CAS(Compare And Swap)概念原理代码演示没有使用CAS的代码运行结果使用CAS的代码运行结果 总结提升 概念说明 ConcurrentHashMap是Ja…...

医疗流程自动化盛行,RPA成为医疗保健行业的重点应用技术
随着我们进入新的科技纪元,机器人流程自动化(RPA)正快速地改变着我们的游戏规则。简单来说,RPA 就是模仿人类与电子系统的互动,自动化执行重复性的任务和操作序列。 医疗保健领域中,RPA 的应用具备巨大的潜…...
Java 版 spring cloud + spring boot 工程系统管理 工程项目管理系统源码 工程项目各模块及其功能点清单
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...
java重试机制实现方案
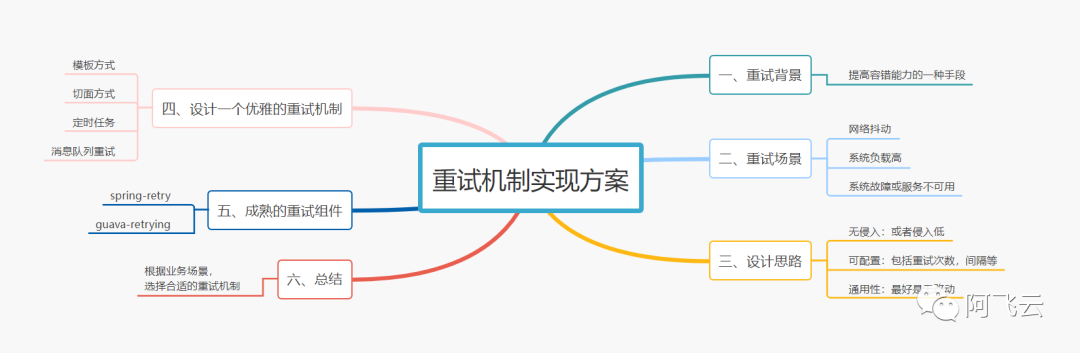
本文内容是目前团队内小磊同学对重试机制实现方案的梳理总结。 从为什么需要重试的背景开始,到重试的场景,大致的一些设计思路,最后通过两个成熟的retry组件进行案例讲解,理论实战。 背景 重试是系统提高容错能力的一种手段。在一…...

参数量仅有50KB的超轻量级unet变种网络egeunet【参数和计算量降低494和160倍】医疗图像分割实践
今天看到一篇挺有意思的文章,做的是跟医疗图像分割相关的工作,但是不像之前看到的一些工作一味地去追求高精度,因为医疗领域本身就是一个相对特殊的行业,对于模型产生的结果的精确性要求是很高的,带来的是参数量级的庞…...
根据需求动态添加删除一级菜单、二级菜单的设置项)
Android10 Settings系列(三)根据需求动态添加删除一级菜单、二级菜单的设置项
一 、背景 当时遇到定制需求,需要根据实际需要隐藏Settings的菜单项,于是开始了寻找方法 二 、准备工作 在看了一下源码,经过尝试后,确认生效后,就简单说明一下Settings中布局中主要组成元素 Settings中的菜单项是由 PreferenceScreen 和Preference组成的。其中Prefer…...
51单片机——串行口通信
目录 1、51单片机串口通信介绍 2、串行口相关寄存器 2.1 、串行口控制寄存器SCON和PCON 2.1.1 SCON:串行控制寄存器 (可位寻址) 2.1.2 PCON:电源控制寄存器(不可位寻址) 2.2、串行口数据缓冲寄存器SBUF 2.3、从机地址控制…...

洛谷题单 Part 6.7.1 矩阵
应队友要求,开始学线性代数,具体路线是矩阵 → \rightarrow →高斯消元 → \rightarrow →线性基。为多项式做个准备 P3390 【模板】矩阵快速幂 题面 板子,用结构体写的,感觉有点丑,一会儿看看题解有没有写得好看的 …...

Spring中c3p0与dbcp配置
<?xml version="1.0" encoding="UTF-8"?> <beans xmlns="http://www.springframework.org/schema/beans" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xmlns:jee="http://www.springframework.org/schem…...

Flutter 添加 example流程
一、已有Flutter工程(命令)添加 example 1、cd 工程(flutter_plugin ,是自己创建的)根目录 例: flutter create example 执行命令创建example PS:cd example 后执行flutter doctor 后就可以看到效果 2、如果需要指定iOS/Android 语言,请添加…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
