(AcWing)集合-Nim游戏
给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。
现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合 S,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 k,表示数字集合 S 中数字的个数。
第二行包含 k 个整数,其中第 i 个整数表示数字集合 S 中的第 i 个数 si。
第三行包含整数 n。
第四行包含 n 个整数,其中第 i 个整数表示第 i 堆石子的数量 hi。
输出格式
如果先手方必胜,则输出 Yes。
否则,输出 No。
数据范围
1≤n,k≤100,
1≤si,hi≤10000
输入样例:
2
2 5
3
2 4 7
输出样例:
Yes#include<iostream>
#include<algorithm>
#include<unordered_set>
#include<cstring>
using namespace std;const int N = 110, M = 10010;int s[N],f[M]; //s用来存储数字集合,f用来存储各状态的sg
int n,m;int sg(int num)
{//如果当前这个数的sg不为-1,说明已被计算过,则直接返回if(f[num]!=-1) return f[num];//定义哈希表,防止出现重复的数字unordered_set<int> S;//对该堆石子进行判断,是否可以拿取集合内的数量的石子,若可以,则将拿去后的状态进行sg(即剩余石子的数量)for(int i=0;i<n;i++) if(num>=s[i]) S.insert(sg(num-s[i]));//对哈希表进行查找,每次将不存在集合中的最小的自然数赋予f[num](即Mex运算),并返回f[num];for(int i=0; ;i++) if(!S.count(i)) return f[num] = i;
}int main()
{cin>>n;for(int i=0;i<n;i++) cin>>s[i];memset(f,-1,sizeof f); //初始化f数组,每个值均为-1int res = 0;cin>>m;//若起点的sg(即初始石子堆的sg)均不为0,则先手必胜//设终点的sg为0,若起点的sg不为0,则可以进行一系列的操作后到0,在这一系列操作中有到0的,有不到0的,不到0的就是获胜的操作//若起点为0,0是最小的自然数,由Mex运算可知,0无法通过任何操作变成非零数,即这就是先手必败for(int i=0;i<m;i++){int num;cin>>num;res^=sg(num);}if(res) cout<<"Yes"<<endl;else cout<<"No"<<endl;return 0;
}
相关文章:
集合-Nim游戏)
(AcWing)集合-Nim游戏
给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。 现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合 S,最后无法进行操作的人视为失败。 问如果两人都采用最优策略,先…...

ConcurrentHashMap源码详解
本文已收录于专栏 《Java》 目录 概念说明数据结构线程安全HashMap示例运行结果ConcurrentHashMap示例运行结果 涉及技术Synchronized概念特性 CAS(Compare And Swap)概念原理代码演示没有使用CAS的代码运行结果使用CAS的代码运行结果 总结提升 概念说明 ConcurrentHashMap是Ja…...

医疗流程自动化盛行,RPA成为医疗保健行业的重点应用技术
随着我们进入新的科技纪元,机器人流程自动化(RPA)正快速地改变着我们的游戏规则。简单来说,RPA 就是模仿人类与电子系统的互动,自动化执行重复性的任务和操作序列。 医疗保健领域中,RPA 的应用具备巨大的潜…...
Java 版 spring cloud + spring boot 工程系统管理 工程项目管理系统源码 工程项目各模块及其功能点清单
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...
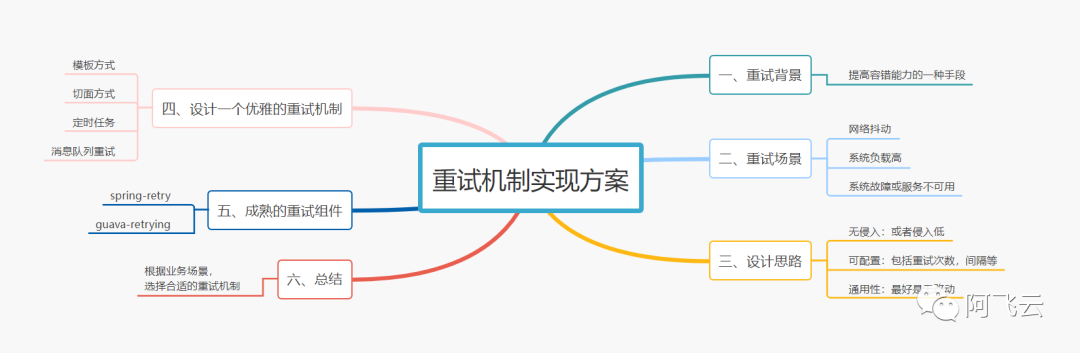
java重试机制实现方案
本文内容是目前团队内小磊同学对重试机制实现方案的梳理总结。 从为什么需要重试的背景开始,到重试的场景,大致的一些设计思路,最后通过两个成熟的retry组件进行案例讲解,理论实战。 背景 重试是系统提高容错能力的一种手段。在一…...

参数量仅有50KB的超轻量级unet变种网络egeunet【参数和计算量降低494和160倍】医疗图像分割实践
今天看到一篇挺有意思的文章,做的是跟医疗图像分割相关的工作,但是不像之前看到的一些工作一味地去追求高精度,因为医疗领域本身就是一个相对特殊的行业,对于模型产生的结果的精确性要求是很高的,带来的是参数量级的庞…...
根据需求动态添加删除一级菜单、二级菜单的设置项)
Android10 Settings系列(三)根据需求动态添加删除一级菜单、二级菜单的设置项
一 、背景 当时遇到定制需求,需要根据实际需要隐藏Settings的菜单项,于是开始了寻找方法 二 、准备工作 在看了一下源码,经过尝试后,确认生效后,就简单说明一下Settings中布局中主要组成元素 Settings中的菜单项是由 PreferenceScreen 和Preference组成的。其中Prefer…...
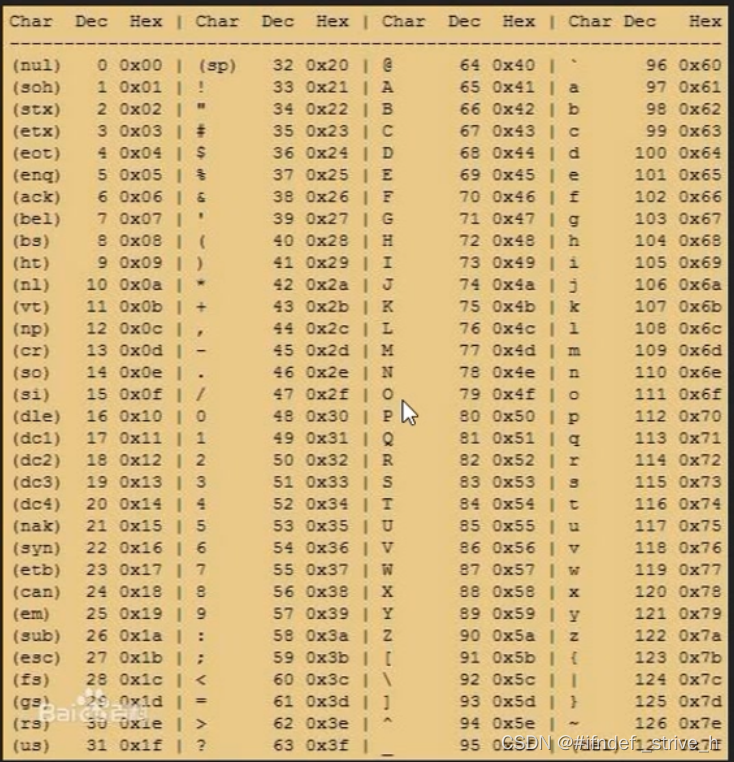
51单片机——串行口通信
目录 1、51单片机串口通信介绍 2、串行口相关寄存器 2.1 、串行口控制寄存器SCON和PCON 2.1.1 SCON:串行控制寄存器 (可位寻址) 2.1.2 PCON:电源控制寄存器(不可位寻址) 2.2、串行口数据缓冲寄存器SBUF 2.3、从机地址控制…...

洛谷题单 Part 6.7.1 矩阵
应队友要求,开始学线性代数,具体路线是矩阵 → \rightarrow →高斯消元 → \rightarrow →线性基。为多项式做个准备 P3390 【模板】矩阵快速幂 题面 板子,用结构体写的,感觉有点丑,一会儿看看题解有没有写得好看的 …...

Spring中c3p0与dbcp配置
<?xml version="1.0" encoding="UTF-8"?> <beans xmlns="http://www.springframework.org/schema/beans" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xmlns:jee="http://www.springframework.org/schem…...

Flutter 添加 example流程
一、已有Flutter工程(命令)添加 example 1、cd 工程(flutter_plugin ,是自己创建的)根目录 例: flutter create example 执行命令创建example PS:cd example 后执行flutter doctor 后就可以看到效果 2、如果需要指定iOS/Android 语言,请添加…...

数据治理8种方法
数据治理8种方法 8种方法,分别是:顶层设计法、技术推动法、应用牵引法、标准先行法、监管驱动法、质量管控法、利益驱动法、项目建设法。 事先声明,这些方法论都是向各位大佬学习来的,也有部分是项目中实操得来的,并非…...

大模型成互联网真正蜕变的标志,亦是各种新技术开始衍生的标志
以往,我们看到了以区块链、元宇宙为代表的诸多新物种的出现,但是,它们始终都没有逃脱仅仅只是一个概念和噱头的宿命,它们始终都没有走出一条可持续的发展道路。说到底,它们仅仅只是一个没有实现商业闭环的概念而已&…...
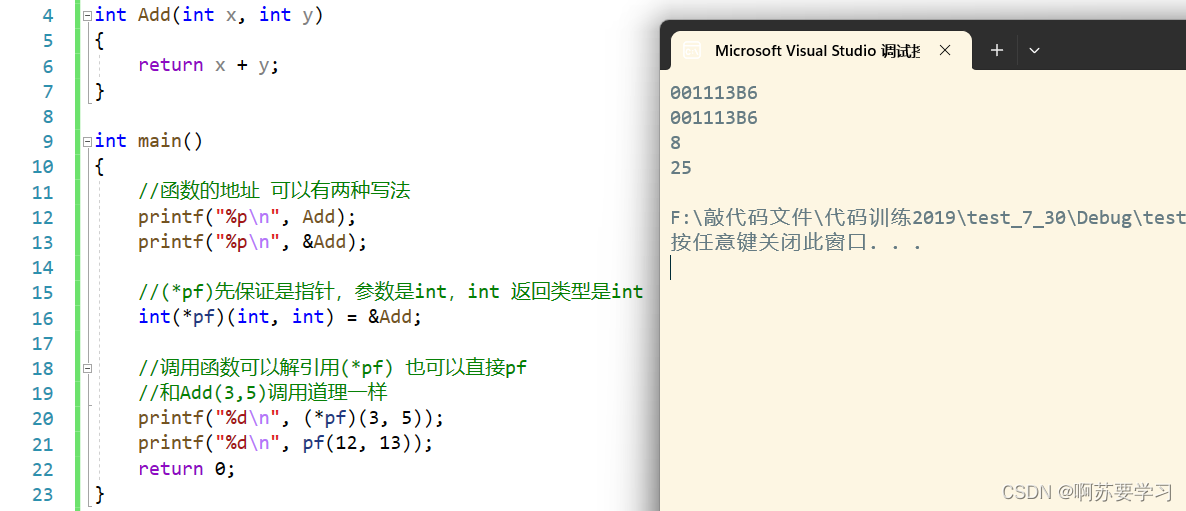
指针进阶详解---C语言
❤博主CSDN:啊苏要学习 ▶专栏分类:C语言◀ C语言的学习,是为我们今后学习其它语言打好基础,C生万物! 开始我们的C语言之旅吧!✈ 目录 前言: 一.字符指针 二.指针数组 三.数组指针 四.数组、指针参数 …...

设计模式思考,简单工厂模式和策略模式的区别?
最近学习了设计模式,学到简单工厂模式和策略模式的时候想,这两个模式不是一样嘛,仔细思考之后发现大体设计思路是一样的,但是细节却有所不一样。 简单工厂模式 简单工厂模式是一种创建型设计模式,它主要涉及对象的创建…...

Java - sh 脚本启动 jar 包等服务 - sh 脚本模板 - 适用于任何类似的服务启动
sh 脚本模板 该模板,每次运行一次都会 kill 掉原来的服务,然后重新启动 jar 包服务 #!/bin/bash# 定义Java进程的名称 APP_NAMEyour-app-name.jar# 定义Java进程的日志文件路径 LOG_PATH/var/log/your-app-name.log# 定义备份日志文件的目录 BACKUP_DI…...

MySQL高级篇第5章(存储引擎)
文章目录 1、查看存储引擎2、设置系统默认的存储引擎3、设置表的存储引擎3.1 创建表时指定存储引擎3.2 修改表的存储引擎 4、引擎介绍4.1 InnoDB 引擎:具备外键支持功能的事务存储引擎4.2 MyISAM 引擎:主要的非事务处理存储引擎4.3 Archive 引擎…...
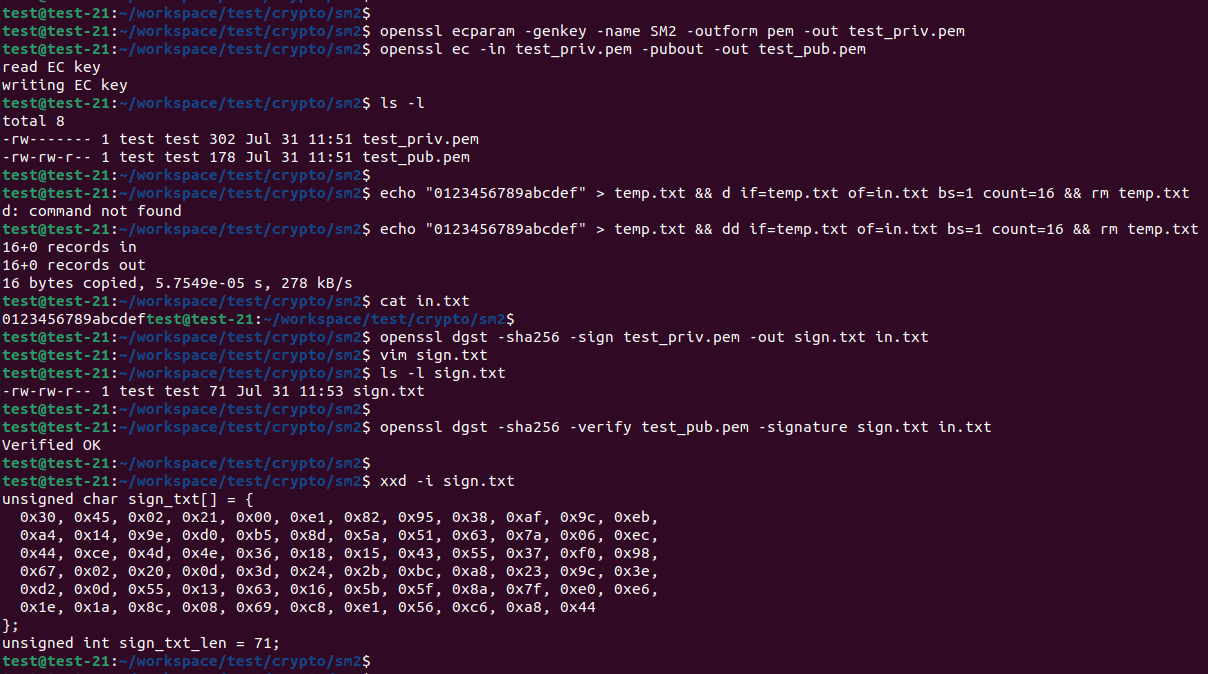
openssl 命令行国密sm2的签名验签操作
快速链接: . 👉👉👉 个人博客笔记导读目录(全部) 👈👈👈 付费专栏-付费课程 【购买须知】: 密码学实践强化训练–【目录】 👈👈👈 生成EC私钥: openssl ecp…...
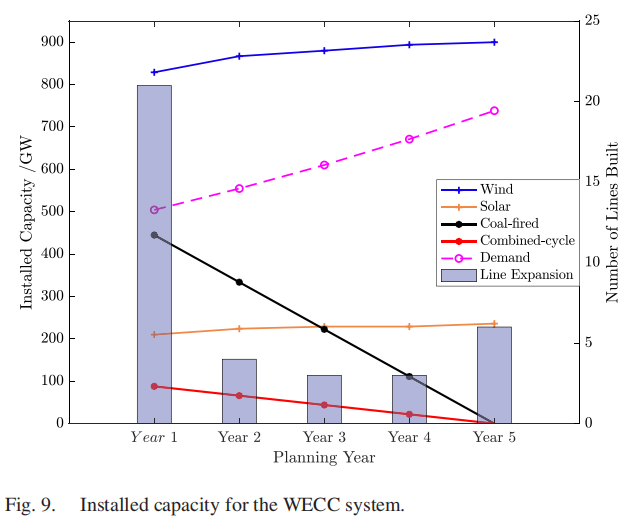
开源代码分享(9)—面向100%清洁能源的发输电系统扩展规划(附matlab代码)
1.背景介绍 1.1摘要 本文提出了一种新颖的建模框架和基于分解的解决策略,将随机规划(SP)和鲁棒优化(RO)相结合,以应对协调中长期电力系统规划中的多重不确定性。从独立系统运营商(ISOÿ…...

为 Google Play 即将推出基于区块链的内容政策做好准备
作者 / Joseph Mills, Group Product Manager, Google Play 作为一个平台,Google Play 一直致力于帮助开发者将创新理念变为现实。Google Play 上托管了许多和区块链相关的应用,我们深知合作伙伴们希望扩展这些应用,并利用 NFT 等代币化数字资…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
