洛谷题单 Part 6.7.1 矩阵
应队友要求,开始学线性代数,具体路线是矩阵 → \rightarrow →高斯消元 → \rightarrow →线性基。为多项式做个准备
P3390 【模板】矩阵快速幂
题面
板子,用结构体写的,感觉有点丑,一会儿看看题解有没有写得好看的
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 110;
const ll mod=1e9+7;
struct node{ll a[N][N];int len;}sqr;
void sqr0(node &x){memset(x.a,0,sizeof x.a);x.len=sqr.len;
}
void sqr1(node &x){memset(x.a,0,sizeof x.a);x.len=sqr.len;for(int i=1;i<=x.len;i++)x.a[i][i]=1;
}
node operator*(node x, node b){node c;sqr0(c);for(int i=1;i<=x.len;i++){for(int j=1;j<=x.len;j++){for(int k=1;k<=x.len;k++)(c.a[i][j]+=x.a[i][k]*b.a[k][j]%mod)%=mod;}}return c;
}void qpow(node &x, ll y){node re;sqr1(re);while(y){if(y&1)re=re*x;x=x*x;y>>=1;}x=re;
}
ll k;
int main(){scanf("%d%lld",&sqr.len,&k);for(int i=1;i<=sqr.len;i++){for(int j=1;j<=sqr.len;j++)scanf("%lld",&sqr.a[i][j]);}qpow(sqr,k);for(int i=1;i<=sqr.len;i++){for(int j=1;j<=sqr.len;j++)printf("%lld ",sqr.a[i][j]);puts("");}
}P1939 【模板】矩阵加速(数列)
题面
搞个方阵
A 3 = [ a 3 a 2 a 1 0 0 0 0 0 0 ] , X = [ 1 1 0 0 0 1 1 0 0 ] , A_3=\left [ \begin{matrix} a_3& a_2 & a_1 \\ 0& 0 &0 \\ 0 & 0 & 0 \\ \end{matrix} \right] ,X=\left [ \begin{matrix} 1& 1 & 0 \\ 0& 0 &1 \\ 1& 0 & 0 \\ \end{matrix} \right], A3= a300a200a100 ,X= 101100010 ,
则 A 3 X = [ a 4 a 3 a 2 0 0 0 0 0 0 ] = A 4 , A_3X=\left [ \begin{matrix} a_4& a_3 & a_2 \\ 0& 0 &0 \\ 0 & 0 & 0 \\ \end{matrix} \right]=A_4, A3X= a400a300a200 =A4,
因此对 X X X进行矩阵快速幂即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5;
const ll mod=1e9+7;
struct node{ll a[N][N];}sqr,A;
void sqr0(node &x){memset(x.a,0,sizeof x.a);
}
void sqr1(node &x){memset(x.a,0,sizeof x.a);for(int i=1;i<=3;i++)x.a[i][i]=1;
}
node operator*(node x, node b){node c;sqr0(c);for(int i=1;i<=3;i++){for(int j=1;j<=3;j++){for(int k=1;k<=3;k++)(c.a[i][j]+=x.a[i][k]*b.a[k][j]%mod)%=mod;}}return c;
}void qpow(node &x, ll y){node re;sqr1(re);while(y){if(y&1)re=re*x;x=x*x;y>>=1;}x=re;
}
ll n,T;
int main(){cin>>T;while(T--){cin>>n;if(n<=3){puts("1");continue;}sqr0(sqr);sqr.a[1][1]=sqr.a[1][2]=sqr.a[2][3]=sqr.a[3][1]=1;sqr0(A);A.a[1][1]=A.a[1][2]=A.a[1][3]=1;qpow(sqr,n-3);A=A*sqr;cout<<A.a[1][1]<<endl;}}P4783 【模板】矩阵求逆
题面
把一个矩阵通过行变换变为单位矩阵所需要的行变换操作,操作给一个单位矩阵,就可以得到其逆矩阵。故应用高斯消元即可。
#include<bits/stdc++.h>
#define N 1000
using namespace std;
const int mod=1e9+7;
inline void read(int &x){int s=0,w=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}while(ch>='0'&&ch<='9'){s=(s<<3)+(s<<1)+(ch&15);ch=getchar();}x=s*w;
}
int n,a[N][N];
int qpow(int x, int y){int re=1;while(y){if(y&1)re=1LL*re*x%mod;x=1LL*x*x%mod,y>>=1;}return re;
}
int main(){read(n);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)read(a[i][j]);a[i][n+i]=1;}for(int i=1;i<=n;i++){int now=i;for(int j=i;j<=n;j++)if(a[now][i]<a[j][i])now=j;if(a[now][i]==0){puts("No Solution");return 0;}if(now!=i)swap(a[now],a[i]);for(int j=i+1;j<=n<<1;j++)a[i][j]=1LL*a[i][j]*qpow(a[i][i],mod-2)%mod;a[i][i]=1;for(int j=1;j<=n;j++){if(j==i)continue;int div=1LL*a[j][i]*qpow(a[i][i],mod-2)%mod;for(int k=i;k<=n<<1;k++)a[j][k]=(a[j][k]-1LL*a[i][k]*div%mod+mod)%mod;}}for(int i=1;i<=n;i++,puts(""))for(int j=1;j<=n;j++)printf("%d ",a[i][n+j]);}
P1962 斐波那契数列
题面
构造矩阵
A 2 = [ f 2 f 1 0 0 ] , X = [ 1 1 1 0 ] , A_2=\left [ \begin{matrix} f_2 & f_1 \\ 0 &0 \\ \end{matrix} \right] ,X=\left [ \begin{matrix} 1& 1 \\ 1& 0 \\ \end{matrix} \right], A2=[f20f10],X=[1110],
则 A 2 X = [ f 3 f 2 0 0 ] = A 3 , A_2X=\left [ \begin{matrix} f_3 & f_2 \\ 0 &0 \\ \end{matrix} \right]=A_3, A2X=[f30f20]=A3,
#include<cstdio>
typedef long long ll;
const ll mod=ll(1e9+7);
struct node
{ll sqr[5][5];
}a;
node operator*(node a, node b)
{node c;c.sqr[1][1]=(a.sqr[1][1]*b.sqr[1][1]%mod+a.sqr[1][2]*b.sqr[2][1]%mod)%mod;c.sqr[1][2]=(a.sqr[1][1]*b.sqr[1][2]%mod+a.sqr[1][2]*b.sqr[2][2]%mod)%mod;c.sqr[2][1]=(a.sqr[2][1]*b.sqr[1][1]%mod+a.sqr[2][2]*b.sqr[2][1]%mod)%mod;c.sqr[2][2]=(a.sqr[2][1]*b.sqr[1][2]%mod+a.sqr[2][2]*b.sqr[2][2]%mod)%mod;return c;
}
ll n;
void quickpow(node &x, ll y)
{node rec;rec.sqr[1][1]=rec.sqr[2][2]=1,rec.sqr[1][2]=rec.sqr[2][1]=0;while(y){if(y&1)rec=rec*x;x=x*x,y>>=1;}x=rec;
}
int main()
{scanf("%lld",&n);if(n==0)return puts("0");a.sqr[1][1]=a.sqr[1][2]=a.sqr[2][1]=1,a.sqr[2][2]=0;quickpow(a,n-1);printf("%lld\n",a.sqr[1][1]);
}
P1349 广义斐波那契数列
题面
构造矩阵
A 2 = [ f 2 f 1 0 0 ] , X = [ P 1 Q 0 ] , A_2=\left [ \begin{matrix} f_2 & f_1 \\ 0 &0 \\ \end{matrix} \right] ,X=\left [ \begin{matrix} P& 1 \\ Q& 0 \\ \end{matrix} \right], A2=[f20f10],X=[PQ10],
则 A 2 X = [ f 3 f 2 0 0 ] = A 3 , A_2X=\left [ \begin{matrix} f_3 & f_2 \\ 0 &0 \\ \end{matrix} \right]=A_3, A2X=[f30f20]=A3,
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod;
struct node
{ll sqr[5][5];node(){memset(sqr,0,sizeof sqr);}
}a,b;
node operator*(node a, node b)
{node c;c.sqr[1][1]=(a.sqr[1][1]*b.sqr[1][1]%mod+a.sqr[1][2]*b.sqr[2][1]%mod)%mod;c.sqr[1][2]=(a.sqr[1][1]*b.sqr[1][2]%mod+a.sqr[1][2]*b.sqr[2][2]%mod)%mod;c.sqr[2][1]=(a.sqr[2][1]*b.sqr[1][1]%mod+a.sqr[2][2]*b.sqr[2][1]%mod)%mod;c.sqr[2][2]=(a.sqr[2][1]*b.sqr[1][2]%mod+a.sqr[2][2]*b.sqr[2][2]%mod)%mod;return c;
}
ll n;
void quickpow(node &x, ll y)
{node rec;rec.sqr[1][1]=rec.sqr[2][2]=1,rec.sqr[1][2]=rec.sqr[2][1]=0;while(y){if(y&1)rec=rec*x;x=x*x,y>>=1;}x=rec;
}
int main()
{scanf("%lld%lld%lld%lld%lld%lld",&a.sqr[1][1],&a.sqr[2][1],&b.sqr[1][2],&b.sqr[1][1],&n,&mod);if(n<=2)return printf("%lld\n",b.sqr[1][3-n]);a.sqr[1][2]=1,a.sqr[2][2]=0;quickpow(a,n-2);b=b*a;printf("%lld\n",b.sqr[1][1]);
}
P4000 斐波那契数列
题面
不是,这什么题都往题单里放啊,这是我 18 18 18年外出集训堵了个论文费了两三天时间才切了的人生中第一道黑题,现在变成紫题了。
有一个性质是 f n m o d p f_n\mod p fnmodp有循环节,且循环节长度不会超过 6 p 6p 6p,这还有个名叫皮萨诺定理。所以我们考虑求出循环节的长度,然后用矩阵乘法求出结果。
引理:对于 f n m o d p f_n\mod p fnmodp的循环节 g ( p ) g(p) g(p)有如下性质:
1. p = p i α i 1.p=p_i^{\alpha_i} 1.p=piαi,即 p p p为质数的幂时, g ( p ) = g ( p i ) × p i α i − 1 g(p)=g(p_i)\times p_i^{\alpha_i-1} g(p)=g(pi)×piαi−1
2. p = ∏ p i α i 2.p=\prod p_i^{\alpha_i} 2.p=∏piαi,即 p p p为合数时, g ( p ) = l c m ( g ( p i α i ) g(p)=lcm(g(p_i^{\alpha_i}) g(p)=lcm(g(piαi)
对于 g ( p ) g(p) g(p)这么算,如果 5 5 5是模 p p p的二次剩余,那么循环节为 p − 1 p-1 p−1的因子,否则为 2 p + 2 2p+2 2p+2的因子。
因为 p p p不是特别大,直接取 p − 1 p-1 p−1和 2 p + 2 2p+2 2p+2即可。
对于 p ≤ 5 p\le 5 p≤5就暴力算即可, g ( 2 ) = 3 , g ( 3 ) = 5 , g ( 5 ) = 20 g(2)=3,g(3)=5,g(5)=20 g(2)=3,g(3)=5,g(5)=20
// luogu-judger-enable-o2
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
#define rg register
typedef long long ll;
char str[30000000];
ll n,p,mod,len,fac[100000],power[100000],faccnt,s;
struct node
{ll sqr[5][5];
}b;
node operator *(node a, node b)
{node xx;xx.sqr[1][1]=(a.sqr[1][1]*b.sqr[1][1]%p+a.sqr[1][2]*b.sqr[2][1]%p)%p;xx.sqr[1][2]=(a.sqr[1][1]*b.sqr[1][2]%p+a.sqr[1][2]*b.sqr[2][2]%p)%p;xx.sqr[2][2]=(a.sqr[2][1]*b.sqr[1][2]%p+a.sqr[2][2]*b.sqr[2][2]%p)%p;xx.sqr[2][1]=(a.sqr[2][1]*b.sqr[1][1]%p+a.sqr[2][2]*b.sqr[2][1]%p)%p;return xx;
}
node quickpow(node x, ll y)
{node rec;rec.sqr[1][1]=rec.sqr[2][2]=1;rec.sqr[1][2]=rec.sqr[2][1]=0;while(y){if(y%2==1)rec=rec*x;x=x*x;y/=2;}return rec;
}
ll gcd(ll a, ll b)
{if(b==0)return a;else return gcd(b,a%b);
}
ll lcm(ll a, ll b)
{return a*b/gcd(a,b);
}
ll get(ll k)
{ll now=k;for(rg ll i=2;i*i<=now;i++){if(now%i==0){faccnt++;fac[faccnt]=i;power[faccnt]=1;while(now%i==0){now/=i;power[faccnt]*=i;}}}for(rg ll i=1;i<=faccnt;i++)power[i]/=fac[i];if(now!=1){fac[++faccnt]=now;power[faccnt]=1;}for(rg ll i=1;i<=faccnt;i++){if(fac[i]==2)power[i]*=3;else if(fac[i]==3)power[i]*=5;else if(fac[i]==5)power[i]*=20;else if(fac[i]%5==1||fac[i]%5==4)power[i]*=fac[i]-1;else power[i]*=(fac[i]+1)<<1;}ll ans=power[1];for(rg ll i=1;i<=faccnt;i++)ans=lcm(ans,power[i]);return ans;
}
int main()
{scanf("%s%lld",str,&p);if(p==1){printf("0\n");return 0;}mod=get(p);len=strlen(str);for(rg ll i=0;i<len;i++)n=((n<<3)+(n<<1)+(str[i]&15))%mod;if(n==0){printf("0\n");return 0;}if(n==1||n==2){printf("1\n");return 0;}b.sqr[2][2]=0;b.sqr[1][1]=b.sqr[1][2]=b.sqr[2][1]=1;b=quickpow(b,n-1);printf("%lld\n",b.sqr[1][1]);
}
P3758 [TJOI2017] 可乐
题面
#include<bits/stdc++.h>
#define N 50
using namespace std;
const int mod=2017;
int t,n,m;
struct node{int a[N][N];node(){memset(a,0,sizeof a);}
}sqr;
node operator*(node x, node b){node c;for(int i=0;i<=n;i++){for(int j=0;j<=n;j++){for(int k=0;k<=n;k++)(c.a[i][j]+=x.a[i][k]*b.a[k][j]%mod)%=mod;}}return c;
}
void qpow(node &x, int y){node re;for(int i=0;i<=n;i++)re.a[i][i]=1;while(y){if(y&1)re=re*x;x=x*x;y>>=1;}x=re;
}
int main(){cin>>n>>m;for(int i=1,u,v;i<=m;i++)cin>>u>>v,sqr.a[u][v]=sqr.a[v][u]=1;cin>>t;for(int i=1;i<=n;i++)sqr.a[i][0]=1;for(int i=0;i<=n;i++)sqr.a[i][i]=1;qpow(sqr,t);int ans=0;for(int i=0;i<=n;i++)(ans+=sqr.a[1][i])%=mod;cout<<ans<<endl;}
P5343 【XR-1】分块
题面
方程很简单 d p [ i ] = ∑ j ∈ b l o c k , j ≤ i d p [ i − j ] dp[i]=\sum_{j\in block,j\le i}dp[i-j] dp[i]=∑j∈block,j≤idp[i−j],现在考虑如何矩阵优化。
由于块的大小不会超过 100 100 100,所以我们开一个 100 × 100 100\times 100 100×100的矩阵,首先预处理出 d p [ 1 ] − d p [ 100 ] dp[1]-dp[100] dp[1]−dp[100],将其填入 A A A矩阵第一行中,再考虑所有 j ∈ b l o c k j\in block j∈block,设 X [ j ] [ 1 ] = 1 X[j][1]=1 X[j][1]=1,对于后99列设 X [ j − 1 ] [ j ] = 1 X[j-1][j]=1 X[j−1][j]=1,则这样可以转移 A A A矩阵,应用矩阵快速幂即可。
#include<bits/stdc++.h>
#define N 120
using namespace std;
const int mod=1e9+7;
const int len=100;
inline void read(int &x){int s=0,w=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}while(ch>='0'&&ch<='9'){s=(s<<3)+(s<<1)+(ch&15);ch=getchar();}x=s*w;
}
long long n;
int p,q,cnt,a[N],f[N],vis[N];
set<int> s;
struct node{int m[N][N];node(){memset(m,0,sizeof m);}
}sqr,A;
node operator*(node a, node b){node c;for(int i=0;i<=len;i++)for(int j=0;j<=len;j++)for(int k=0;k<=len;k++)c.m[i][j]=int((1LL*c.m[i][j]+1LL*a.m[i][k]*b.m[k][j]%mod)%mod);return c;
}
void qpow(node &x, long long y){node re;for(int i=0;i<=len;i++)re.m[i][i]=1;while(y){if(y&1)re=re*x;x=x*x;y>>=1;}x=re;
}
int main(){cin>>n;read(p);for(int i=1,x;i<=p;i++){read(x);if(s.find(x)==s.end())s.insert(x);}read(q);for(int i=1,x;i<=q;i++){read(x);if(s.find(x)!=s.end()&&!vis[x])a[++cnt]=x,vis[x]=1;}f[0]=1;for(int i=1;i<=len;i++)for(int j=1;j<=cnt;j++)if(a[j]<=i)f[i]=(1LL*f[i]+f[i-a[j]])%mod;if(n<=100){printf("%d\n",f[n]);return 0;}for(int i=0;i<=len;i++)sqr.m[0][len-i]=f[i];for(int i=1;i<=cnt;i++)A.m[a[i]-1][0]=1;for(int i=1;i<=len;i++)A.m[i-1][i]=1;qpow(A,n-100);sqr=sqr*A;printf("%d\n",sqr.m[0][0]);return 0;
}
相关文章:

洛谷题单 Part 6.7.1 矩阵
应队友要求,开始学线性代数,具体路线是矩阵 → \rightarrow →高斯消元 → \rightarrow →线性基。为多项式做个准备 P3390 【模板】矩阵快速幂 题面 板子,用结构体写的,感觉有点丑,一会儿看看题解有没有写得好看的 …...

Spring中c3p0与dbcp配置
<?xml version="1.0" encoding="UTF-8"?> <beans xmlns="http://www.springframework.org/schema/beans" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xmlns:jee="http://www.springframework.org/schem…...

Flutter 添加 example流程
一、已有Flutter工程(命令)添加 example 1、cd 工程(flutter_plugin ,是自己创建的)根目录 例: flutter create example 执行命令创建example PS:cd example 后执行flutter doctor 后就可以看到效果 2、如果需要指定iOS/Android 语言,请添加…...

数据治理8种方法
数据治理8种方法 8种方法,分别是:顶层设计法、技术推动法、应用牵引法、标准先行法、监管驱动法、质量管控法、利益驱动法、项目建设法。 事先声明,这些方法论都是向各位大佬学习来的,也有部分是项目中实操得来的,并非…...

大模型成互联网真正蜕变的标志,亦是各种新技术开始衍生的标志
以往,我们看到了以区块链、元宇宙为代表的诸多新物种的出现,但是,它们始终都没有逃脱仅仅只是一个概念和噱头的宿命,它们始终都没有走出一条可持续的发展道路。说到底,它们仅仅只是一个没有实现商业闭环的概念而已&…...
指针进阶详解---C语言
❤博主CSDN:啊苏要学习 ▶专栏分类:C语言◀ C语言的学习,是为我们今后学习其它语言打好基础,C生万物! 开始我们的C语言之旅吧!✈ 目录 前言: 一.字符指针 二.指针数组 三.数组指针 四.数组、指针参数 …...

设计模式思考,简单工厂模式和策略模式的区别?
最近学习了设计模式,学到简单工厂模式和策略模式的时候想,这两个模式不是一样嘛,仔细思考之后发现大体设计思路是一样的,但是细节却有所不一样。 简单工厂模式 简单工厂模式是一种创建型设计模式,它主要涉及对象的创建…...

Java - sh 脚本启动 jar 包等服务 - sh 脚本模板 - 适用于任何类似的服务启动
sh 脚本模板 该模板,每次运行一次都会 kill 掉原来的服务,然后重新启动 jar 包服务 #!/bin/bash# 定义Java进程的名称 APP_NAMEyour-app-name.jar# 定义Java进程的日志文件路径 LOG_PATH/var/log/your-app-name.log# 定义备份日志文件的目录 BACKUP_DI…...

MySQL高级篇第5章(存储引擎)
文章目录 1、查看存储引擎2、设置系统默认的存储引擎3、设置表的存储引擎3.1 创建表时指定存储引擎3.2 修改表的存储引擎 4、引擎介绍4.1 InnoDB 引擎:具备外键支持功能的事务存储引擎4.2 MyISAM 引擎:主要的非事务处理存储引擎4.3 Archive 引擎…...
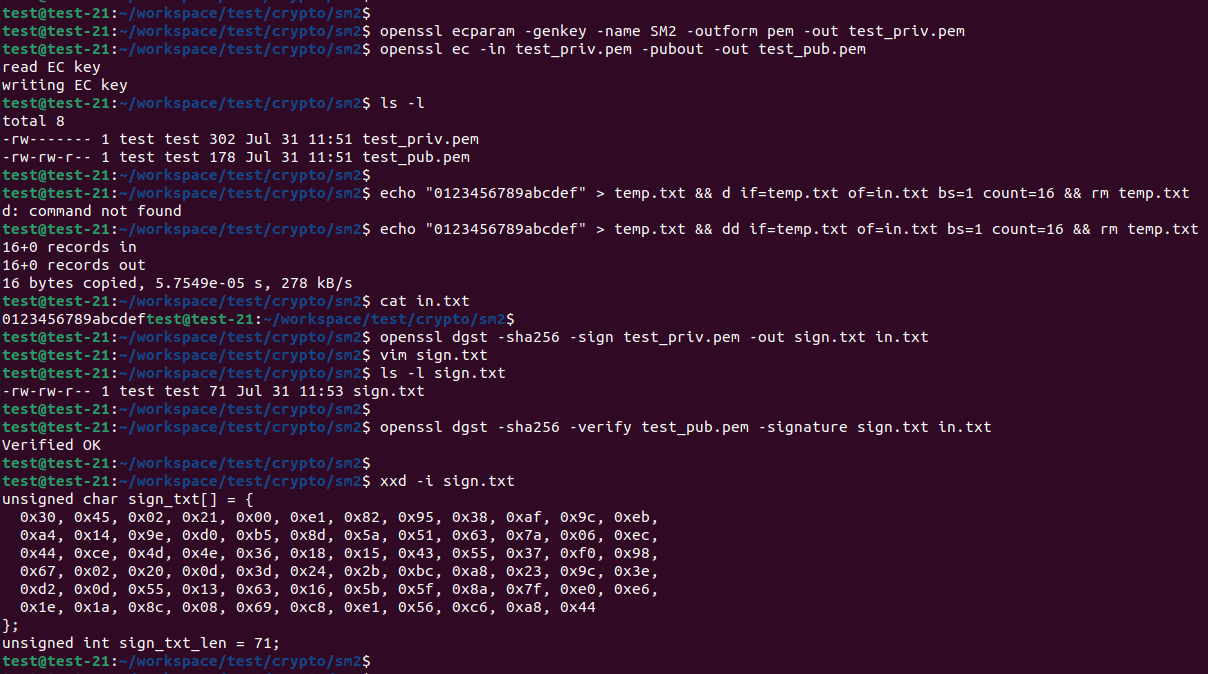
openssl 命令行国密sm2的签名验签操作
快速链接: . 👉👉👉 个人博客笔记导读目录(全部) 👈👈👈 付费专栏-付费课程 【购买须知】: 密码学实践强化训练–【目录】 👈👈👈 生成EC私钥: openssl ecp…...
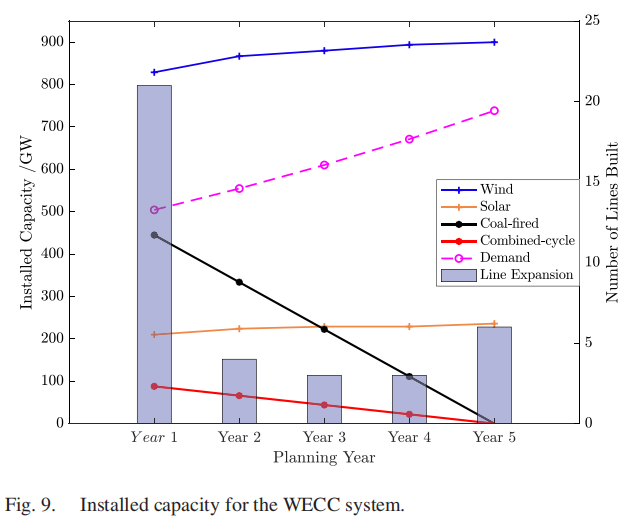
开源代码分享(9)—面向100%清洁能源的发输电系统扩展规划(附matlab代码)
1.背景介绍 1.1摘要 本文提出了一种新颖的建模框架和基于分解的解决策略,将随机规划(SP)和鲁棒优化(RO)相结合,以应对协调中长期电力系统规划中的多重不确定性。从独立系统运营商(ISOÿ…...

为 Google Play 即将推出基于区块链的内容政策做好准备
作者 / Joseph Mills, Group Product Manager, Google Play 作为一个平台,Google Play 一直致力于帮助开发者将创新理念变为现实。Google Play 上托管了许多和区块链相关的应用,我们深知合作伙伴们希望扩展这些应用,并利用 NFT 等代币化数字资…...

查找-多路查找详解篇
多路查找树 多路查找树(Multway Search Tree)是一种高级的树形数据结构,它 允许每个节点有多个子节点(通常大于等于2)。多路查找树的每个节点 可以存储多个关键字和对应的值。分类 2-3树(2-3 Tree&#x…...
css设置八等分圆
现需要上图样式的布局,我通过两张向右方的图片,通过定位和旋转完成了布局。 问题: 由于是通过旋转获取到的样式,实际的盒子是一个长方形,当鼠标移入对应的箭头时选中的可能是其他盒子,如第一张设计稿可以看…...

「教程」如何使用一套代码在多种程序中接入天气预警API
引言 天气预警的重要性不言而喻,在遭受自然灾害和极端天气时,及时获得预警信息可以拯救生命和减少财产损失。如今,随着科技的进步,开发者和企业可以借助天气预警 API 这款强大的服务,将实时预警信息集成到自己的应用中…...
(MYSQL)数据库服务端的启动与停止,登录与退出
MYSQL服务的启动与停止 方式一:右击左下角win图标——选择计算机管理——选择计算机管理(本地)——选择服务和应用程序——找到mysql(此方法不好用) 方式二:通过管理员身份运行(必须是管理员身…...

数学建模学习(8):单目标和多目标规划
优化问题描述 优化 优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值 线性规划 线性规划是指目标函数和约束都是线性的情况 [x,fval]linprog(f,A,b,Aeq,Beq,LB,U…...

【Vscode | R | Win】R Markdown转html记录-Win
Rmd文件转html R语言环境Vscode扩展安装及配置配置radian R依赖包pandoc安装配置pandoc环境变量验证是否有效转rmd为html 注意本文代码块均为R语言代码,在R语言环境下执行即可 R语言环境 官网中去下载R语言安装包以及R-tool 可自行搜寻教程 无需下载Rstudio Vscod…...

【Lua语法】字符串操作、字符串中的方法
1.对字符串的操作 --声明一个字符串 str "我是一个字符串"--1.获取字符串的长度 -- 前面加个#即可(注意:Lua中字母占1个长度,汉字占3个长度) print(#str)--2.字符串多行打印 -- 方法1.Lua中是支持转义字符的 print("哈哈\n嘻嘻&q…...

Linux 终端生成二维码
1、安装qrencode [rootnode1 script]# yum -y install qrencode2、输出正常的 [rootnode1 ~]# echo https://www.github.com|qrencode -o - -t utf83、输出彩色的 [rootnode1 ~]# qrencode -t utf8 -s 1 https://www.github.com|lolcatPS:没有lolcat命令 #由于…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
