查找-多路查找详解篇
多路查找树
多路查找树(Multway Search Tree)是一种高级的树形数据结构,它
允许每个节点有多个子节点(通常大于等于2)。多路查找树的每个节点
可以存储多个关键字和对应的值。
分类
2-3树(2-3 Tree):
2-3树是一种最简单的多路查找树,每个节点可以存储1个或2个关键字,
并有2个或3个子节点。
2-3树的特点是所有叶子节点都在同一层,且根节点到每个叶子节点的
路径长度相等,保持树的平衡性。B-树(B-tree):
B-树是一种平衡的多路查找树,每个节点可以存储多个关键字,并有相
应数量的子节点。
B-树的特点是节点的关键字按照升序排列,具有高度平衡的特性,主要
用于在磁盘等外部存储设备中高效存储和检索数据。B+树(B+ tree):
B+树是B-树的一种变种,在B-树的基础上做了一些优化,特别适合于范
围查询和顺序访问。
B+树的特点是只有叶子节点存储了真实数据,而内部节点仅用于索引,
叶子节点通过指针连接形成一个链表,方便范围查询。B树(B-tree):
B*树也是B-树的一种变种,与B+树类似,它在B-树的基础上做了一些改
进。
B*树通过在非叶子节点中存储部分关键字,扩大了节点的使用率,减少
了磁盘访问次数,并提高了空间和时间的效率。Trie树(字典树或前缀树):
Trie树是一种特殊的多路查找树,在处理字符串和前缀匹配的情况下非
常有用。
Trie树的特点是每个节点代表一个字符,从根节点到叶子节点的路径可
以表示一个完整的字符串。除此以外,还有如2-3-4树、2-3-4-树、B*+树等。每种多路查找树在
平衡性、存储结构、查询性能等方面可能有所不同,选择合适的多路查
找树取决于应用需求和数据特点。对于大规模的外部存储数据,B-树和
B+树是常见的选择;对于高效的字符串匹配和前缀查询,Trie树是一种
有效的数据结构。
详细介绍
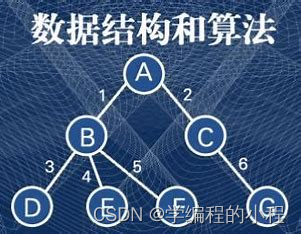
2-3树(2-3 Tree)
2-3树是一种平衡的多路查找树,每个节点可以存储1个或2个关键字,并有2个
或3个子节点。以下是关于2-3树的详细介绍:
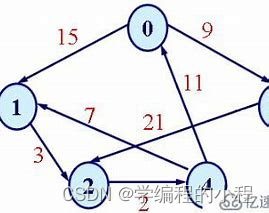
结构特点:
2-3树由节点组成,每个节点可以存储1个或2个关键字,这些关键字按升序排列。
每个节点有2个或3个子节点,对应于存储的关键字个数。
所有叶子节点都在同一层,且根节点到每个叶子节点的路径长度相等,保持树的
平衡性。
插入操作:
1、当要插入一个关键字时,从根节点开始,判断关键字应插入的位置。
2、如果节点已满(即已有两个关键字),则需要进行节点分裂操作。将中间较大的关键字移动到上一层的父节点,并将两个剩余的关键字分别创建为新的子节点。
3、如果节点还没有满,则直接将关键字插入到正确的位置。
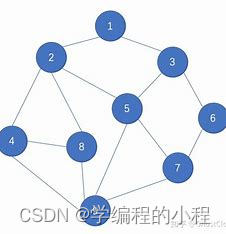
删除操作:
当要删除一个关键字时,从根节点开始,找到包含该关键字的节点。如果该节点是叶子节点,直接删除关键字即可。如果该节点是内部节点,有几种情况需要处理:如果该节点有2个关键字,则可以直接删除关键字,不需要做其他操作。如果该节点有1个关键字:如果其兄弟节点有2个关键字,则可以借用兄弟节点的一个关键字,并进行相关的调整。如果其兄弟节点也只有1个关键字,则需要进行合并操作,将关键字和子节点合并到一起。
查询操作:
2-3树的查询操作与二叉查找树类似,从根节点开始,根据关键字的大小比较,
向左或向右子节点递归查询,直到找到匹配的关键字或遇到叶子节点。
强调
2-3树的特点在于其每个节点可以存储多个关键字,这样可以减少树的高度,提
供更高效的搜索和插入操作。它保持了树的平衡性,且所有叶子节点都在同一层,
这样可以保证较为平衡的查询性能。然而,2-3树的实现和维护操作较为复杂,
导致其并不常用,更常见的是其变种B-树和B+树,它们在2-3树的基础上进行了
一些优化和改进。
Java代码实现
// 2-3树的节点类
class Node {private int[] keys; // 节点的关键字private Node[] children; // 子节点数组private int size; // 节点包含的关键字数量private boolean isLeaf; // 是否为叶子节点public Node(boolean isLeaf) {this.keys = new int[3];this.children = new Node[4];this.size = 0;this.isLeaf = isLeaf;}// 从节点中查找关键字的位置public int findKey(int key) {for (int i = 0; i < size; i++) {if (keys[i] == key) {return i;} else if (keys[i] > key) {return -1;}}return -1;}// 在节点中插入关键字public void insertKey(int key) {if (size == 0) {keys[0] = key;size++;} else {int i = size - 1;while (i >= 0 && keys[i] > key) {keys[i + 1] = keys[i];i--;}keys[i + 1] = key;size++;}}// 在节点中删除关键字public void deleteKey(int key) {int index = findKey(key);if (index != -1) {for (int i = index; i < size - 1; i++) {keys[i] = keys[i + 1];}size--;}}// 获取节点的关键字数量public int getSize() {return size;}// 判断节点是否为叶子节点public boolean isLeaf() {return isLeaf;}// 获取节点指定位置的子节点public Node getChild(int index) {return children[index];}// 设置节点指定位置的子节点public void setChild(int index, Node child) {children[index] = child;}
}// 2-3树类
class TwoThreeTree {private Node root;public TwoThreeTree() {root = null;}// 在2-3树中插入关键字public void insert(int key) {if (root == null) {root = new Node(true);root.insertKey(key);} else {Node newNode = insertKey(root, key);if (newNode != null) {Node oldRoot = root;root = new Node(false);root.setChild(0, oldRoot);root.setChild(1, newNode);root.insertKey(newNode.keys[0]);root.insertKey(oldRoot.keys[0]);}}}// 在给定的节点中插入关键字private Node insertKey(Node node, int key) {if (node.isLeaf()) {node.insertKey(key);if (node.getSize() > 2) {return splitLeaf(node);}} else {int i = node.getSize() - 1;while (i >= 0 && key < node.getChild(i).keys[0]) {i--;}Node newNode = insertKey(node.getChild(i + 1), key);if (newNode != null) {node.insertKey(newNode.keys[0]);}
B-树(B-tree)
B-树(B-tree)是一种平衡的多路查找树,广泛应用于在磁盘等外部存储设备中
高效地存储和检索大量数据。以下是关于B-树的详细介绍:
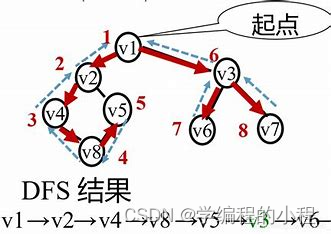
结构特点:
B-树由节点组成,每个节点可以存储多个
关键字,这些关键字按升序排列。
B-树的特点是节点的关键字按升序排列,具有高度平衡的特性。
每个节点通常有多个子节点,最多可以拥有m个子节点,其中m称为B-树的阶数。
插入操作:
1、当要插入一个关键字时,从根节点开始,判断关键字应插入的位置。
2、如果节点已满,则需要进行节点分裂操作。将中间位置的关键字提升为父节点,并将节点分裂为两个节点,将剩余的关键字均匀分配到这两个节点中。
3、如果要插入的节点还没有满,则直接将关键字插入到合适的位置。
删除操作:
1、当要删除一个关键字时,从根节点开始,找到包含该关键字的节点。
2、如果该节点是叶子节点,直接删除关键字即可。如果该节点是内部节点,需要找到其前驱或后继关键字来替代删除的关键字。
3、在删除操作后,如果节点中的关键字数量过少,则需要进行节点合并或者从兄弟节点中借用关键字来保持树的平衡。
查询操作:
B-树的查询操作与二叉查找树类似,从根节点开始,根据关键字的大小比较,
向左或向右子节点递归查询,直到找到匹配的关键字或遇到叶子节点。

强调
B-树适用于大规模数据存储和查询的场景,尤其是需要在外部存储设备上进行操
作的情况。B-树的高度平衡保证了较为均衡的查询性能,因为从根节点到叶子节
点的路径长度相等或差别不大。B-树的阶数m可以根据具体应用和硬件限制来选
择,通常情况下,较大的阶数有助于减少磁盘访问的次数,提高效率。B-树的变种B+树在B-树的基础上做了一些优化,将所有数据存储在叶子节点中,
使得范围查询和顺序访问更加高效。因此,在现代数据库系统和文件系统中,
B+树更加常见和广泛应用。
代码实现
import java.util.ArrayList;
import java.util.List;class BMinusTreeNode {public boolean isLeaf; // 是否是叶子节点public List<Integer> keys; // 节点中存储的关键字public List<BMinusTreeNode> children; // 节点的子节点public BMinusTreeNode() {keys = new ArrayList<>();children = new ArrayList<>();}
}class BMinusTree {private BMinusTreeNode root;private int t; // B-树的阶数public BMinusTree(int degree) {root = new BMinusTreeNode();root.isLeaf = true;t = degree;}public void insert(int key) {// 根节点满了就分裂if (root.keys.size() == (2 * t)) {BMinusTreeNode newRoot = new BMinusTreeNode();newRoot.children.add(root);splitChild(newRoot, 0, root);root = newRoot;}insertNonFull(root, key);}private void insertNonFull(BMinusTreeNode node, int key) {int index = node.keys.size() - 1;if (node.isLeaf) {while (index >= 0 && node.keys.get(index) > key) {index--;}node.keys.add(index + 1, key);} else {while (index >= 0 && node.keys.get(index) > key) {index--;}index++;if (node.children.get(index).keys.size() == (2 * t)) {splitChild(node, index, node.children.get(index));if (node.keys.get(index) < key) {index++;}}insertNonFull(node.children.get(index), key);}}private void splitChild(BMinusTreeNode parent, int index, BMinusTreeNode node) {BMinusTreeNode newNode = new BMinusTreeNode();newNode.isLeaf = node.isLeaf;parent.keys.add(index, node.keys.get(t - 1));parent.children.add(index + 1, newNode);for (int i = t; i < 2 * t - 1; i++) {newNode.keys.add(node.keys.get(i));}if (!node.isLeaf) {for (int i = t; i < 2 * t; i++) {newNode.children.add(node.children.get(i));}}for (int i = 2 * t - 2; i >= t - 1; i--) {node.keys.remove(i);}if (!node.isLeaf) {for (int i = 2 * t - 1; i >= t; i--) {node.children.remove(i);}}}
B+树(B+tree)
B+树(B+ tree)是B-树的一种变种,特别适用于范围查询和顺序访问。
结构特点:
B+树与B-树类似,由节点组成,每个节点可以存储多个关键字,这些关键字按升
序排列。B+树的特点是只有叶子节点存储了真实数据,而内部节点仅用于索引。叶子节点
通过指针连接形成一个链表,方便范围查询和顺序访问。
内部节点特点:
内部节点存储关键字和指向子节点的指针。
内部节点的关键字按升序排列,用于指示范围查询的起点。
内部节点的指针指向比关键字更大的子节点。
叶子节点特点:
叶子节点存储真实数据和指向下一个叶子节点的指针。
叶子节点的关键字按升序排列,支持范围查询和顺序访问。
所有叶子节点通过指针连接成一个链表,便于范围查询和顺序访问。
插入操作:
当要插入一个关键字时,从根节点开始,找到合适的叶子节点。
如果叶子节点已满,则需要进行节点分裂操作。将中间位置的关键字提升到父节
点,并将两个剩余的部分分别创建为新的叶子节点。
如果叶子节点还没有满,则直接将关键字插入到合适的位置。
删除操作:
当要删除一个关键字时,从根节点开始,找到包含该关键字的叶子节点。
直接删除叶子节点中的关键字,并更新链表指针。
删除操作后,如果叶子节点的关键字个数过少,则需要从兄弟节点借用关键字或
进行节点合并。
查询操作:
B+树的查询操作与B-树类似,从根节点开始,根据关键字的大小比较,向左或向右子节点递归查询,直到找到匹配的关键字或遇到叶子节点。
对于范围查询和顺序访问,可以从叶子节点开始,沿着链表进行遍历。
强调
B+树的特点在于只有叶子节点存储真实数据,这样使得范围查询和顺序访问更加
高效,因为数据在叶子节点上连续存储,读取连续的数据块比随机读取更快。而
内部节点仅存储索引信息,可以容纳更多的索引,提高了查询效率。B+树的实现
适用于需要高效地处理大量数据的数据库和文件系统,能够提供较高的查询性能
和存储效率。代码实现
import java.util.ArrayList;
import java.util.List;class BPlusTreeNode {public boolean isLeaf;public List<Integer> keys;public List<Object> values;public List<BPlusTreeNode> children;public BPlusTreeNode next;public BPlusTreeNode() {isLeaf = false;keys = new ArrayList<>();values = new ArrayList<>();children = new ArrayList<>();next = null;}
}class BPlusTree {private BPlusTreeNode root;private int m;public BPlusTree(int m) {root = new BPlusTreeNode();root.isLeaf = true;this.m = m;}// 插入操作public void insert(int key, Object value) {if (root.keys.size() == m) {BPlusTreeNode newRoot = new BPlusTreeNode();newRoot.children.add(root);splitChild(newRoot, 0, root);root = newRoot;}insertNonFull(root, key, value);}// 非满子节点插入操作private void insertNonFull(BPlusTreeNode node, int key, Object value) {int index = node.keys.size() - 1;if (node.isLeaf) {while (index >= 0 && node.keys.get(index) > key) {index--;}node.keys.add(index + 1, key);node.values.add(index + 1, value);node.next = node.next;} else {while (index >= 0 && node.keys.get(index) > key) {index--;}index++;if (node.children.get(index).keys.size() == m) {splitChild(node, index, node.children.get(index));if (node.keys.get(index) < key) {index++;}}insertNonFull(node.children.get(index), key, value);}}// 分裂满子节点private void splitChild(BPlusTreeNode parent, int index, BPlusTreeNode node) {BPlusTreeNode newNode = new BPlusTreeNode();newNode.isLeaf = node.isLeaf;parent.keys.add(index, node.keys.get(m / 2));parent.children.add(index + 1, newNode);newNode.keys.addAll(node.keys.subList((m / 2) + 1, m));newNode.values.addAll(node.values.subList((m / 2) + 1, m));if (!node.isLeaf) {newNode.children.addAll(node.children.subList((m / 2) + 1, m + 1));node.children.subList((m / 2) + 1, m + 1).clear();} else {newNode.next = node.next;node.next = newNode;}node.keys.subList(m / 2, m).clear();node.values.subList(m / 2, m).clear();}// 搜索操作public List<Object> search(int key) {return search(root, key);}private List<Object> search(BPlusTreeNode node, int key) {int index = 0;while (index < node.keys.size() && key > node.keys.get(index)) {index++;}if (index < node.keys.size() && key == node.keys.get(index)) {return node.values.get(index);} else if (node.isLeaf) {return null;} else {return search(node.children.get(index), key);}}
}
B树(B-tree)
B树(B-tree)是一种平衡的多路查找树,主要用于在磁盘等外部存储设备中高
效地存储和检索大量数据。以下是关于B树的详细介绍:
结构特点:
B树由节点组成,每个节点可以存储多个关键字,这些关键字按升序排列。
B树的特点是节点的关键字按升序排列,具有高度平衡的特性。
每个节点通常有多个子节点,最多可以拥有m个子节点,其中m称为B树的阶数。
插入操作:
当要插入一个关键字时,从根节点开始,判断关键字应插入的位置。
如果节点已满(即已有m-1个关键字),则需要进行节点分裂操作。将中间位置
的关键字提升为父节点,并将节点分裂为两个节点,将剩余的关键字均匀分配到
这两个节点中。
如果要插入的节点还没有满,则直接将关键字插入到合适的位置。
删除操作:
当要删除一个关键字时,从根节点开始,找到包含该关键字的节点。
如果该节点是叶子节点,直接删除关键字。
如果该节点是内部节点,有几种情况需要处理:
如果该节点有足够多的关键字,则可以直接删除关键字。
如果该节点的关键字数量过少,需要考虑兄弟节点的关键字数量以及兄弟节点合
并的情况。
查询操作:
B树的查询操作与二叉查找树类似,从根节点开始,根据关键字的大小比较,向
左或向右子节点递归查询,直到找到匹配的关键字或遇到叶子节点。
B树适用于大规模数据存储和查询的场景,特别适用于外部存储设备上的数据存
储。其平衡性保证了较为均衡的查询性能,因为从根节点到叶子节点的路径长度
相等或差别不大。B树的阶数m可以根据具体应用和硬件限制来选择,较大的阶数
有助于减少磁盘访问的次数,提高效率。
强调
B树的变种B+树在B树的基础上做了一些优化,将所有的数据都存储在叶子节点
中,使得范围查询和顺序访问更加高效。因此,B+树在现代数据库系统和文件
系统中更为常见和广泛应用。、
代码实现
import java.util.ArrayList;
import java.util.List;class BTreeNode {int degree; // B树的阶数List<Integer> keys; // 节点中存储的关键字List<BTreeNode> children; // 节点的子节点boolean isLeaf; // 是否是叶子节点public BTreeNode(int degree, boolean isLeaf) {this.degree = degree;this.isLeaf = isLeaf;keys = new ArrayList<>();children = new ArrayList<>();}
}class BTree {BTreeNode root; // B树的根节点int degree; // B树的阶数public BTree(int degree) {this.degree = degree;root = new BTreeNode(degree, true);}// 插入关键字public void insert(int key) {if (root.keys.size() == (2 * degree - 1)) {BTreeNode newRoot = new BTreeNode(degree, false);newRoot.children.add(root);splitChild(newRoot, 0, root);root = newRoot;}insertNonFull(root, key);}// 在非满节点插入关键字private void insertNonFull(BTreeNode node, int key) {int index = node.keys.size() - 1;if (node.isLeaf) {while (index >= 0 && key < node.keys.get(index)) {index--;}node.keys.add(index + 1, key);} else {while (index >= 0 && key < node.keys.get(index)) {index--;}index++;if (node.children.get(index).keys.size() == (2 * degree - 1)) {splitChild(node, index, node.children.get(index));if (key > node.keys.get(index)) {index++;}}insertNonFull(node.children.get(index), key);}}// 分裂子节点private void splitChild(BTreeNode parent, int index, BTreeNode node) {BTreeNode newNode = new BTreeNode(degree, node.isLeaf);parent.keys.add(index, node.keys.get(degree - 1));parent.children.add(index + 1, newNode);for (int i = 0; i < degree - 1; i++) {newNode.keys.add(node.keys.get(i + degree));if (!node.isLeaf) {newNode.children.add(node.children.get(i + degree));}}if (!node.isLeaf) {newNode.children.add(node.children.get(2 * degree - 1));}for (int i = degree - 1; i >= 0; i--) {node.keys.remove(i + degree - 1);if (!node.isLeaf) {node.children.remove(i + degree);}}}// 搜索关键字public boolean search(int key) {return search(root, key);}private boolean search(BTreeNode node, int key) {int index = 0;while (index < node.keys.size() && key > node.keys.get(index)) {index++;}if (index < node.keys.size() && key == node.keys.get(index)) {return true;} else if (node.isLeaf) {return false;} else {return search(node.children.get(index), key);}}
}
Trie树(字典树或前缀树)
Trie树,也被称为字典树或前缀树,是一种用于高效存储和搜索字符串的树型数
据结构。Trie树的主要特点是通过字符串的前缀来进行搜索和匹配。
结构特点:
Trie树由根节点和一系列子节点组成。
根节点不包含任何关键字,每个子节点都表示一个字符,并按字符的顺序连接形
成路径。
从根节点到每个叶子节点的路径都对应一个字符串。
每个节点可以存储额外的信息,如词频或附加数据等。
插入操作:
当要插入一个字符串时,从根节点开始,逐个字符按顺序插入。
如果某个字符对应的子节点不存在,则创建一个新的子节点。
插入字符串的最后一个字符后,将当前节点标记为一个单词的结束。
搜索操作:
当要搜索一个字符串时,从根节点开始,逐个字符按顺序匹配。
如果某个字符对应的子节点存在,则继续匹配下一个字符。
如果匹配遇到缺失的字符或到达某个节点后没有子节点,则表示字符串不在Trie
树中。
如果匹配成功并且在Trie树中找到最后一个字符,则表示字符串存在于Trie树中。
删除操作:
当要删除一个字符串时,从根节点开始,逐个字符按顺序遍历。
如果遍历过程中发现某个字符对应的子节点不存在,则表示字符串不存在于Trie
树中。
如果遍历成功,并到达字符串的最后一个字符,将当前节点的结束标记取消。
如果遍历成功,但还存在其他相关字符串(例如,删除"abc"但还有"abcd"),
可以保留当前节点以表示其他相关字符串。
优点:
搜索的时间复杂度与字符串长度无关,仅与Trie树的高度相关,通常比哈希表更
高效。
可以高效地搜索具有相同前缀的字符串集合。
对于字符串的前缀匹配和自动补全,Trie树可以提供高效的结果。
缺点:
空间消耗较大,尤其在处理大量长字符串时。为了缓解这个问题,可以使用压缩
的Trie树,如压缩前缀树(Patricia树)或Trie树的变种来减少存储空间。
代码实现
class TrieNode {private TrieNode[] children;private boolean isEndOfWord;public TrieNode() {children = new TrieNode[26]; // 26个英文字母isEndOfWord = false;}public TrieNode getChild(char ch) {return children[ch - 'a'];}public void setChild(char ch, TrieNode node) {children[ch - 'a'] = node;}public boolean isEndOfWord() {return isEndOfWord;}public void setEndOfWord(boolean isEndOfWord) {this.isEndOfWord = isEndOfWord;}
}class Trie {private TrieNode root;public Trie() {root = new TrieNode();}public void insert(String word) {TrieNode node = root;for (char ch : word.toCharArray()) {if (node.getChild(ch) == null) {node.setChild(ch, new TrieNode());}node = node.getChild(ch);}node.setEndOfWord(true);}public boolean search(String word) {TrieNode node = findNode(word);return node != null && node.isEndOfWord();}public boolean startsWith(String prefix) {TrieNode node = findNode(prefix);return node != null;}private TrieNode findNode(String str) {TrieNode node = root;for (char ch : str.toCharArray()) {node = node.getChild(ch);if (node == null) {return null;}}return node;}
}
使用示例
public class Main {public static void main(String[] args) {Trie trie = new Trie();trie.insert("apple");trie.insert("banana");trie.insert("grape");System.out.println(trie.search("apple")); // 输出: trueSystem.out.println(trie.search("orange")); // 输出: falseSystem.out.println(trie.startsWith("app")); // 输出: trueSystem.out.println(trie.startsWith("ban")); // 输出: trueSystem.out.println(trie.startsWith("grap")); // 输出: true}
}
相关文章:

查找-多路查找详解篇
多路查找树 多路查找树(Multway Search Tree)是一种高级的树形数据结构,它 允许每个节点有多个子节点(通常大于等于2)。多路查找树的每个节点 可以存储多个关键字和对应的值。分类 2-3树(2-3 Tree&#x…...
css设置八等分圆
现需要上图样式的布局,我通过两张向右方的图片,通过定位和旋转完成了布局。 问题: 由于是通过旋转获取到的样式,实际的盒子是一个长方形,当鼠标移入对应的箭头时选中的可能是其他盒子,如第一张设计稿可以看…...

「教程」如何使用一套代码在多种程序中接入天气预警API
引言 天气预警的重要性不言而喻,在遭受自然灾害和极端天气时,及时获得预警信息可以拯救生命和减少财产损失。如今,随着科技的进步,开发者和企业可以借助天气预警 API 这款强大的服务,将实时预警信息集成到自己的应用中…...
(MYSQL)数据库服务端的启动与停止,登录与退出
MYSQL服务的启动与停止 方式一:右击左下角win图标——选择计算机管理——选择计算机管理(本地)——选择服务和应用程序——找到mysql(此方法不好用) 方式二:通过管理员身份运行(必须是管理员身…...

数学建模学习(8):单目标和多目标规划
优化问题描述 优化 优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值 线性规划 线性规划是指目标函数和约束都是线性的情况 [x,fval]linprog(f,A,b,Aeq,Beq,LB,U…...

【Vscode | R | Win】R Markdown转html记录-Win
Rmd文件转html R语言环境Vscode扩展安装及配置配置radian R依赖包pandoc安装配置pandoc环境变量验证是否有效转rmd为html 注意本文代码块均为R语言代码,在R语言环境下执行即可 R语言环境 官网中去下载R语言安装包以及R-tool 可自行搜寻教程 无需下载Rstudio Vscod…...

【Lua语法】字符串操作、字符串中的方法
1.对字符串的操作 --声明一个字符串 str "我是一个字符串"--1.获取字符串的长度 -- 前面加个#即可(注意:Lua中字母占1个长度,汉字占3个长度) print(#str)--2.字符串多行打印 -- 方法1.Lua中是支持转义字符的 print("哈哈\n嘻嘻&q…...

Linux 终端生成二维码
1、安装qrencode [rootnode1 script]# yum -y install qrencode2、输出正常的 [rootnode1 ~]# echo https://www.github.com|qrencode -o - -t utf83、输出彩色的 [rootnode1 ~]# qrencode -t utf8 -s 1 https://www.github.com|lolcatPS:没有lolcat命令 #由于…...
子组件未抛出事件 父组件如何通过$refs监听子组件中数据的变化
我们平时开发项目会使用一些比较成熟的组件库, 但是在极小的情况下,可能会出现我们需要监听某个属性的变化,使我们的页面根据这个属性发生一些改变,但是偏偏组件库没有把这个属性抛出来,当我们使用watch通过refs监听时,由于生命周期的原因还不能拿到,这时候我们可以这样做,以下…...
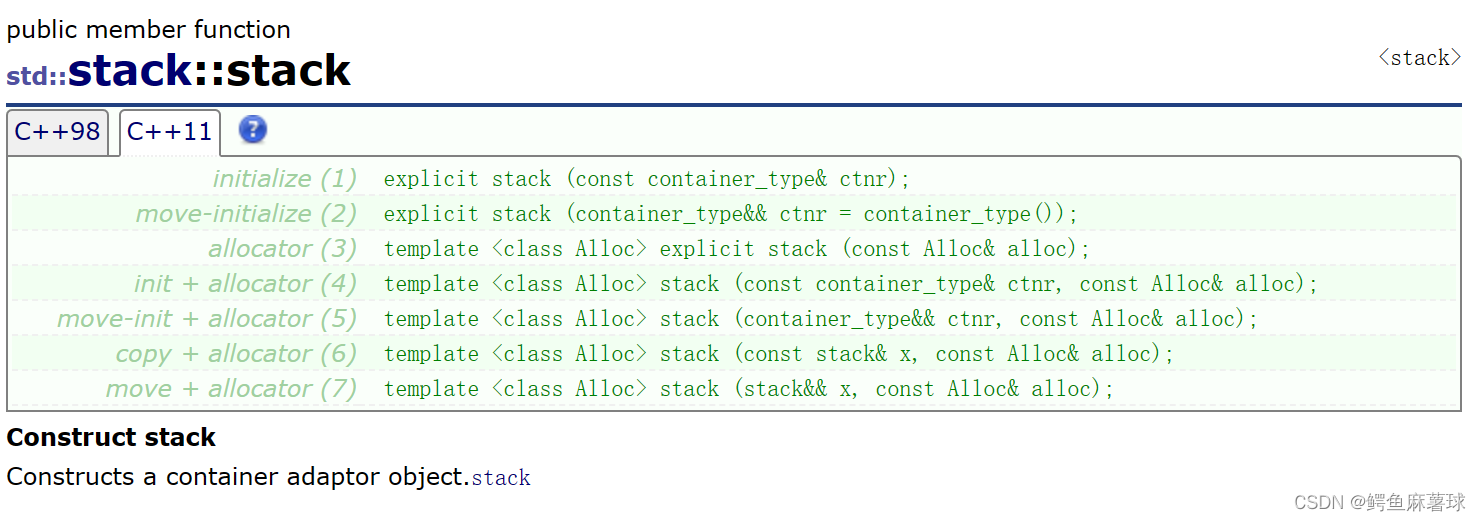
【C++】STL——stack的介绍和使用、stack的push和pop函数介绍和使用、stack的其他成员函数
文章目录 1.stack的介绍2.stack的使用2.1stack构造函数2.1stack成员函数(1)empty() 检测stack是否为空(2)size() 返回stack中元素的个数(3)top() 返回栈顶元素的引用(4)push() 将元素…...
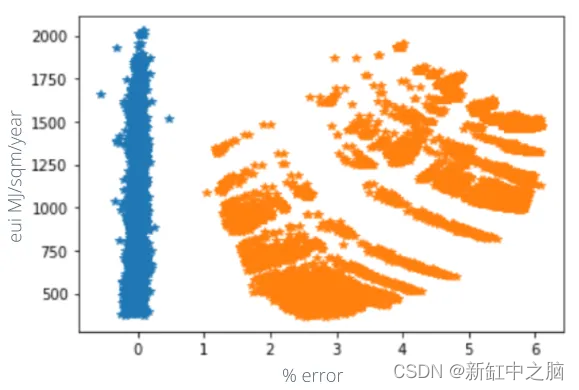
基于BIM+AI的建筑能源优化模型【神经网络】
推荐:用 NSDT设计器 快速搭建可编程3D场景。 AEC(建筑、工程、施工)行业的BIM 技术,允许在实际施工开始之前虚拟地建造建筑物; 这带来了许多有形和无形的好处:减少成本超支、更有效的协调、增强决策权等等。…...

#P0998. [NOIP2007普及组] 守望者的逃离
题目背景 恶魔猎手尤迪安野心勃勃,他背叛了暗夜精灵,率领深藏在海底的娜迦族企图叛变。 题目描述 守望者在与尤迪安的交锋中遭遇了围杀,被困在一个荒芜的大岛上。 为了杀死守望者,尤迪安开始对这个荒岛施咒,这座岛…...
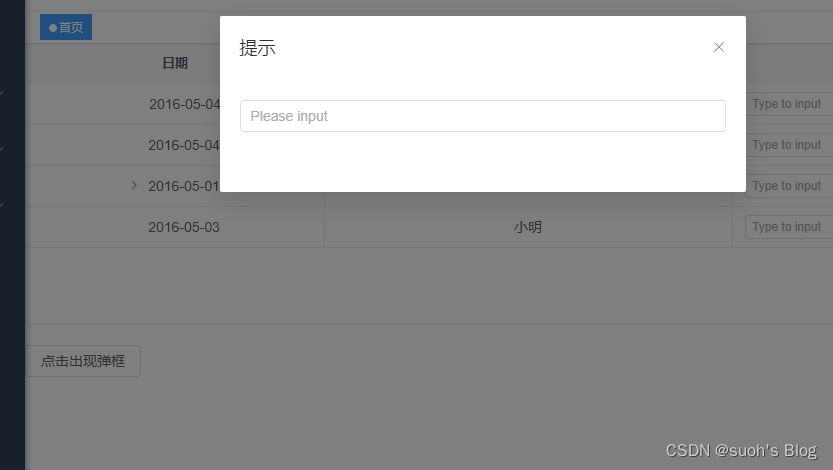
vue3+ts+elementui-plus二次封装弹框
一、弹框组件BaseDialog <template><div classmain><el-dialog v-model"visible" :title"title" :width"dialogWidth" :before-close"handleClose"><!-- 内容插槽 --><slot></slot><template…...

ffmpeg批量分割视频解决视频前几秒黑屏的问题解决
echo 请输入视频地址: set /p fp echo 请输入开始时间: set /p st echo 请输入结束时间: set /p et echo 请输入分片时间: set /p sgt echo 注意:循环范围参数要空格。 for /l %%i in (%st%, %sgt%, %et%) do call :aa…...

nodejs + express 调用本地 python程序
假设已经安装好 nodejs ; cd /js/node_js ; 安装在当前目录的 node_modules/ npm install express --save 或者 cnpm install express --save web 服务器程序 server.js const http require(http); const express require(express); const path require(path); const …...

微信小程序代码优化3个小技巧
抽取重复样式 样式复用 我们会发现很多时候在开发的过程中会存在多个页面中都用到了同样的样式,那么其实之前有提到过,公用样式可以放在app.wxss里面这样就可以直接复用。 如:flex布局的纵向排列,定义在app.wxss里面 .flex-co…...
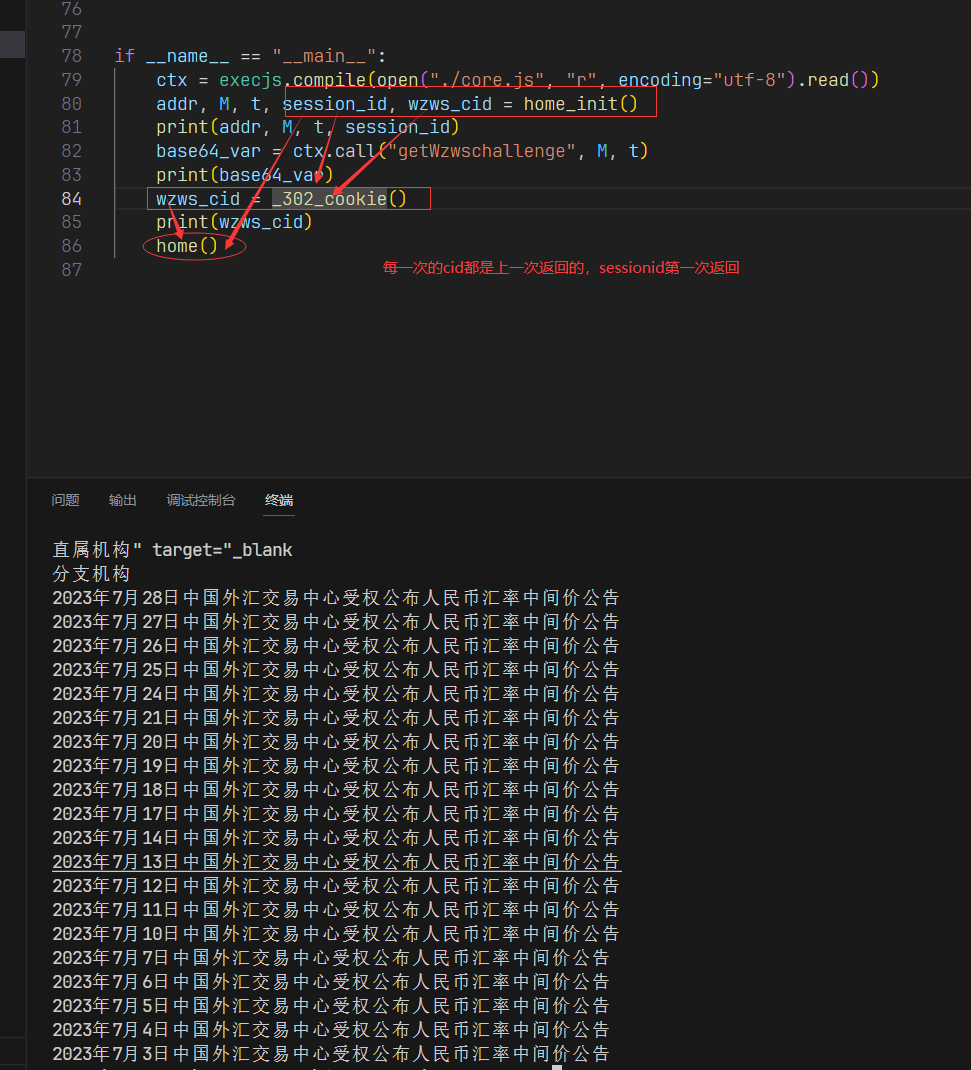
某行动态cookie反爬虫分析
某行动态cookie反爬虫分析 1. 预览 反爬网址(base64): aHR0cDovL3d3dy5wYmMuZ292LmNu 反爬截图: 需要先加载运行js代码,可能是对环境进行检测,反调试之类的 无限debugger 处理办法 网上大部分人说的都是添加cookie来解决。 那个noscript…...

恒运资本:A股、港股全线爆发,沪指突破3300点,恒指重返2万点上方
7月31日,两市股指高开高走,沪指在金融、地产、酿酒等权重板块的带动下一举突破3300点。截至发稿,沪指、深成指、创业板指涨幅均超1%,上证50指数涨近2%。Wind数据显现,北向资金净买入超25亿元。 职业方面,券…...

Rust vs Go:常用语法对比(十二)
题图来自 Rust vs Go in 2023[1] 221. Remove all non-digits characters Create string t from string s, keeping only digit characters 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. 删除所有非数字字符 package mainimport ( "fmt" "regexp")func main() { s : hei…...
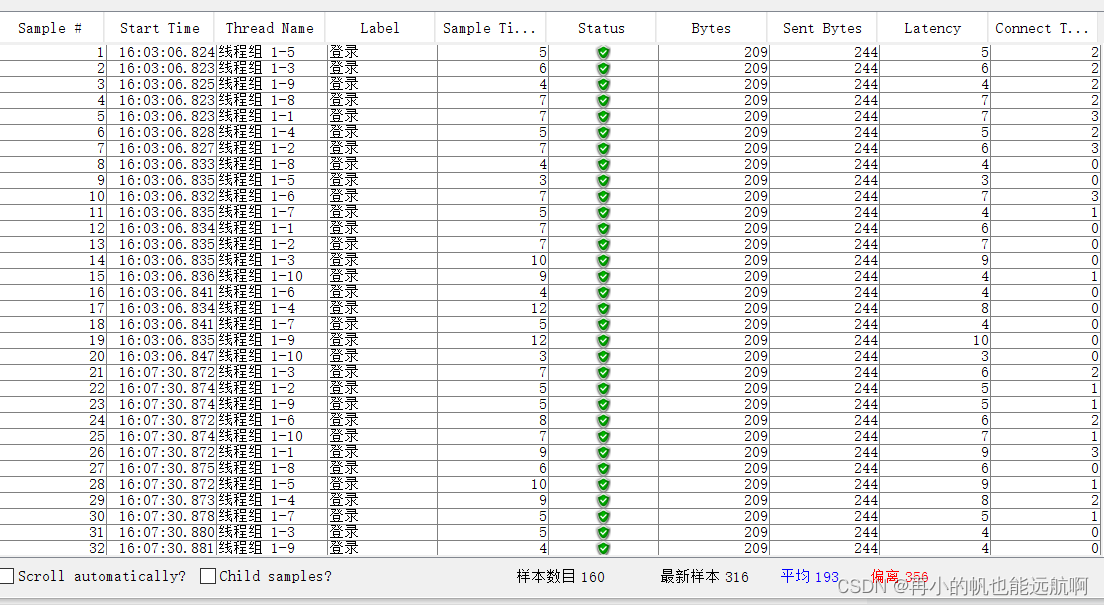
jmeter接口测试、压力测试简单实现
jmeter测试的组件执行顺序: 测试计划—>线程组—>配置元件—>前置处理器—>定时器—>逻辑控制器—>取样器—>后置处理器—>断言—>监听器 组件的作用范围: 同级组件同级组件下的子组件父组件 目前市面上的三类接口 1、基…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
