开源代码分享(9)—面向100%清洁能源的发输电系统扩展规划(附matlab代码)
1.背景介绍
1.1摘要
本文提出了一种新颖的建模框架和基于分解的解决策略,将随机规划(SP)和鲁棒优化(RO)相结合,以应对协调中长期电力系统规划中的多重不确定性。从独立系统运营商(ISO)的角度出发,问题被建模为一个多年的发电和输电规划问题,旨在最小化二进制和连续不确定性下的扩展和运营成本,即系统元件事故和负荷/发电变化。RO利用经修正的事故准则来捕捉N-k事故,而SP嵌入RO通过使用具有时空相关性的历史数据生成操作场景来考虑负荷/发电不确定性。原始混合模型非常复杂,但通过基于列-约束生成和L型算法的分解策略可以减轻其复杂性。我们应用我们的模型来进行长期系统规划,研究了高比例可再生能源渗透度的情况,以及长期规划中100%可再生能源的情况。在多尺度测试系统上进行的数值实验验证了所提出方法的有效性。
1.2引言
对于高可再生能源渗透的电力系统的运营模式和经济状况的研究,引起了学术界和工业界的广泛关注。可再生能源虽然具有清洁能源和零运营成本的优势,但其随机发电模式对电力系统的可靠性构成了挑战,尤其是当电网需要为突发情况提供高水平的备用能力时。因此,尽管美国政府和更广泛的社区极力鼓励可再生能源投资[1],但在高渗透可再生能源的情况下的系统规划仍需要进一步研究。
迄今为止,研究人员已经在基于不确定性的系统规划方面做了广泛的工作[2]-[5]。从ISO的角度来看,发电机和输电线路是最大的可靠性问题,这在许多运行问题中经常存在,例如机组组合问题[6]和输电规划问题[2]。鲁棒优化(RO)可以有效应对这种不确定性,具体描述在[2]和[7]中。RO的基本思想是找到最坏情况,然后做出预防性决策,这也使解决方案高度保守。另一方面,可再生能源和弹性需求的不确定性是系统规划师面临的另一个挑战。大量的文献(例如[8]和[9])也采用RO来处理这种不确定性,通过设置保守边界。然而,相对而言,随机规划(SP)比RO提供了较少保守的解决方案,我们可以利用历史数据生成场景。特别是对于具有高可再生能源渗透的大型系统,通过场景生成,如蒙特卡洛模拟结合多阶段场景树[10],能够准确捕捉可再生能源和需求的时空相关性。
在当今的输电网络中,不确定性层出不穷,例如发电机/线路的二进制状态和持续发电/负荷的波动性。因此,将SP和RO结合起来是一种具有更高可靠性的有前途的方法。最近,许多研究也考虑了融合了持续形式的混合SP和RO形式,如[3]、[5]和[11],但这仅对不确定性进行了有限的评估。很少有研究同时考虑电力系统元件的事故和随机发电,尤其是在高可再生能源渗透水平下的发电和输电扩展问题(G&TEP)中。
由于其非凸性和涉及的不确定性,G&TEP在多重不确定性下的联合优化是一个棘手的问题。A. Moreira等人[4]在连续不确定性中融合了二进制事故,但没有探索改进算法以促进解决方案。L. Gallego等人[12]使用启发式算法来避免求解复杂的模型,但得到的是局部最优解。然而,评估所获得的最优解与全局最优解之间的差距并不容易。我们认为,在像电力系统规划这样可能涉及多个规划年份且不需要实时解决的大规模经济评估中,如果我们能获得一个保证的全局最优解,将是更好的选择。这可以看作是我们提出的方法与那些智能方法相比的优势。此外,大多数现有的研究解决单年度规划问题[11]、[13]、[14],这些问题并未涵盖电力系统规划的某些方面,如发电机投产或退役的时机。然而,在我们的研究中,我们的目标是调查在系统中进行超高可再生能源安装是否有益。由于可再生单位被广泛认为是没有变动运行成本的单位[15],可再生能源投资的经济回报可能在长期内超过传统单位。因此,为了确保对不同发电技术进行公正比较,我们还考虑了投资成本并拟揭示可再生能源投资的成本效益,尤其是在超高可再生能源渗透案例下。
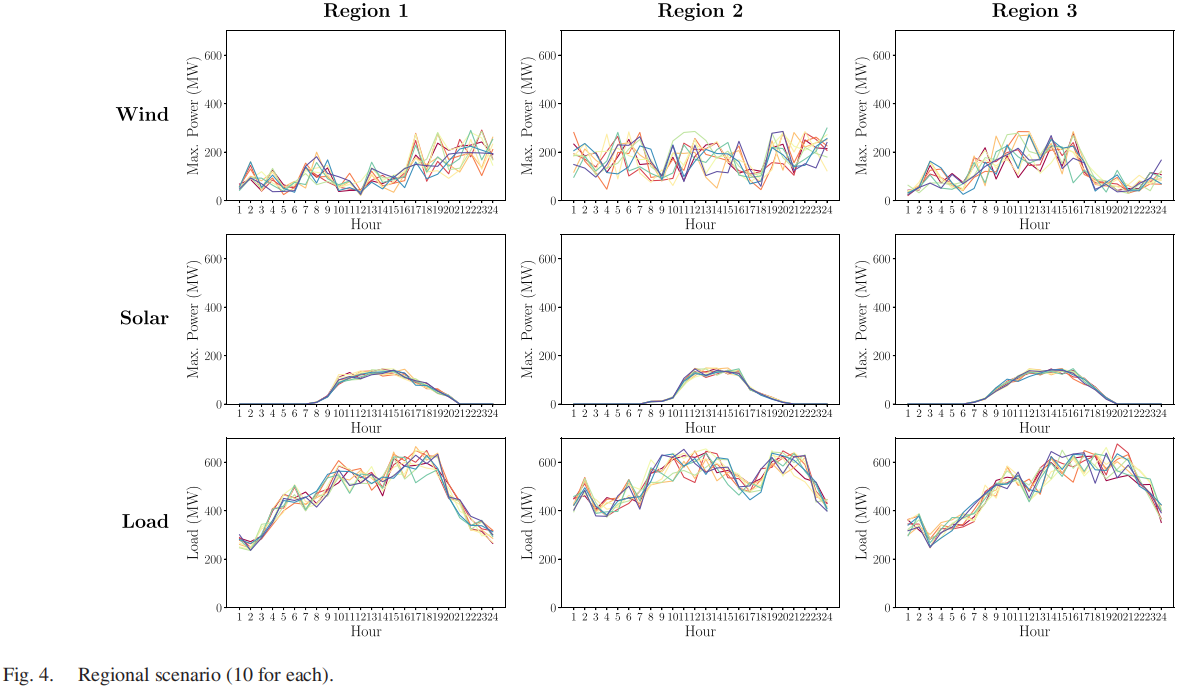
为了研究百分之百可再生能源的系统,可再生能源之间的相关性也是至关重要的,例如不同地区的风能,风能和太阳能,风能和需求等。在任何时刻,系统应该有足够的可再生能源发电量来满足需求。然而,系统规划者必须采取系统范围的方法,考虑区域间的相互支持,避免特定位置的发电短缺。此外,即使在发生N-k线路故障的情况下,充足的输电能力对于区域间能源交换以保持系统能量平衡至关重要。最终的最优G&TEP投资应考虑到最佳的发电组合和长期的可再生能源发电前景。一些研究人员(例如[14])认为,100%可再生能源的盈利能力不如传统能源发电组合,但这实际上对系统设置非常敏感。
在本文中,我们提出了一种有效的G&TEP建模和解决方案方法,以实现100%可再生能源渗透。[16]提出的柱塔与约束生成(C&CG)方法可以将我们的问题分解为一个主问题和一个子问题。这种方法已被[3]、[6]、[11]等许多研究采用,并成为多阶段RO问题的主流解决方法。此外,正如[11]和[4]中报道的那样,解决子问题消耗了大部分计算时间。我们提出应用L形法[17]来进一步促进子问题的求解,这也可以实现并行计算。同时,我们特别考虑基于蒙特卡罗采样的区域可再生能源对短期和长期时空相关性与负载之间的相关性。图1提供了我们提出的方法的总体框架。

与最先进的研究相比,本文的主要贡献有三个方面。
1) 我们分析了在超高水平的可再生能源渗透下的协调系统规划,并通过特定参数设置,在IEEE测试系统和WECC系统上调查了100%可再生能源渗透可能存在的问题。
2) 为了应对G&TEP中的多重不确定性,我们提出了一个三阶段的多年鲁棒共优化模型,其中包含随机调整模型。鲁棒对偶模型捕捉到了N-k容错,而基于样本的情景考虑了可再生能源与负载之间的时空相关性,实现了需求和可再生能源的不确定性。
3) 我们利用C&CG算法将整个问题分解为主从结构,并基于对偶理论改进了随机子问题,并采用L形法进行了分解。这大大提高了计算效率,多尺度测试案例验证了所提出的方法的有效性。
本文的其余部分安排如下:第三节描述了G&TEP模型的数学表达;第四节介绍了所提出的解决策略和详细的流程图;案例研究和可扩展性测试分别在第五节和第六节分析;第七节对本文进行总结,并提出几点意见。
2.数学模型
在本节中,我们将详细介绍复合不确定性G&TEP的数学模型。首先,我们将展示混合SP和RO模型的三阶段确定等效形式(DEF)。在此,我们所提到的“阶段”指的是所提出的优化框架的数学结构。




目标函数(1)描述了提议的发电机和输电线路扩建的投资成本,以及计划的常规发电机的运行成本和可能的负荷削减。
约束条件(1a)-(1b)对发电机和输电线路的投资预算进行建模,并构建了第一阶段的可行区域。约束条件(1c)-(1e)表示一旦在第t年进行了投资,该组件将在规划时间的剩余部分可用。控制集合N(∗,t)表示候选单位和规划时间之间的映射,我们根据可投资的年限对候选单位进行分类。这些约束条件构成了第一阶段的约束空间。约束条件(1f)显示了发电机和输电线路的N-k准则,其中Kt可以调整以执行不同的应急分析。该约束条件是第二阶段的不确定性集合[18]的形式(第二阶段的目标函数可以被视为{0 a},其中a是故障指标的向量)。该不确定性集合是离散多面体。
对于第三阶段,我们首先解释t和h之间的关系。由于我们考虑的是长期规划问题,在整个一年的8760个小时上进行遍历会给模型带来很重的复杂性。因此,我们考虑第三阶段采用24小时运行作为对一个典型日的小时调度进行分析。这种操作在[14]中也被采用。然后,时间索引映射集合M可以描述为
![]()
此外,我们还注意到该设计进一步推广了选择代表性小时/天的应用。当系统规划师打算选择更多代表性小时进行G&TEP研究时,通过增加小时数来调整集合M是微不足道的。这也表明我们提出的框架非常灵活和通用,可以根据系统规划师在G&TEP问题中的需求进行扩展。
值得注意的是,我们公式中的故障指标是以天为基准的变量。正如我们所指出的,第三阶段问题可以视为一个24小时的经济调度问题。对于这种运行问题,通常在整个运行周期内,即24小时内,考虑事故情况[19]。实际上,94%的计划和运行中的故障持续时间超过2小时,其中34.6%的故障持续时间超过48小时[20]。在一些系统规划的研究中,也采用了长期的应急情况[5]。为了简化起见,由于我们选择了一年中的一天作为多个不确定情景的代表性日期,我们稍微滥用了符号,并使用一个以年为基准的索引来表示以天为基准的变量,例如aG g,t。此外,对于第三阶段的运营问题,我们选择使用一个具有多个情景的代表性日进行研究,以调查区域可再生能源和负荷之间的短期相关性,这可以通过小时级的运营更好地捕捉,正如[14]中所采用的方式。
特别地,约束条件(1g)是节点平衡约束,约束条件(1h)定义了直流线路流动方程。需要注意的是,这里我们稍微滥用了符号,使得单位电抗A'在系统基准MVA下应进行归一化处理。约束条件(1i)-(1l)是候选线路和现有线路的线路流量限制约束。约束条件(1m)-(1p)是候选发电机和现有常规发电机以及可再生发电机的发电能力约束。需要注意的是,可再生发电机可以进行调度,因此我们允许可再生能源的削减。约束条件(1q)表示相位角限制。我们可以发现,所有第三阶段的变量都与情景索引ω相关联,用于不同可再生能源和负荷实现的不同情况。需要注意的是,二进制变量和变量的乘法,比如(1h),(1i),(1j),(1m)和(1o),使得该模型成为混合整数非线性模型。
所提出的模型(1)是基于混合随机和鲁棒优化的系统规划的非常通用的框架,并且可以轻松调整或扩展以包括更多关于各种研究方向或工业应用的约束条件。例如,在我们的案例研究中,我们没有任何现有的发电机,因此可以在公式中忽略约束条件(1n)和(1p)。我们还修改了(1)以包含独特的案例设置,例如区域N-1容错和一个候选母线的多个投资,可以通过将约束条件(1f)替换为(1r)并分别添加约束条件(1s)来实现,如下所示。

其中,z表示区域指示符,Z是总区域集合,ncg表示热力发电机的候选母线,ncr表示可再生发电机的候选母线。
3.模型求解方法

在所描述的模型的第三部分中,提出了一个难以解决的三阶段混合整数非线性问题,其中包含随机补偿。然而,我们可以将原始问题分解为一个混合整数线性规划(MILP)主问题和一个混合整数双线性子问题的结构,可以基于C&CG算法的理论进行迭代求解[16]。线性放松技术可以处理子问题的非线性。此外,可以使用L形法对子问题进行进一步的分解[17]。
图2描述了整体的解决方案工作流程。通常,我们采用C&CG算法将问题分解为主-从结构,然后L形算法根据不同的场景进一步对子问题进行分解。我们将在问题的描述中解释图2的过程和符号表示。为了更简洁,下面使用了紧凑的形式。
3.1主问题
在C&CG过程中,我们将主问题表示为式(2)。其中x表示一阶段变量,z表示第三阶段变量,其迭代索引为k,包含当前迭代k之前的所有过去迭代的信息。IC和PC表示投资成本和惩罚成本的向量,而pG和r表示发电机出力和负荷放弃的向量。φ是一个辅助变量,用来构建第二阶段问题的松弛下界。第三阶段变量的约束条件为式(2d)。需要注意的是,这里的第二阶段变量a是固定的,它们是从子问题中获取的。因此,主问题现在成为一个确定性的混合整数线性规划问题,可以通过现成的求解器有效地求解。这里,x包括一阶段变量,z包括第三阶段变量。
![]()

3.2子问题
C&CG程序的子问题是由第二和第三阶段问题构建而成的,即确定情景下最坏情况的问题。在这里,变量a包括第二阶段的变量。

请注意,约束中的第一阶段变量成为了在上一次迭代中从主问题中获得的固定参数。由于(3)的内最小化问题具有线性规划特性,根据强对偶理论,在给出第二阶段的客观句柄后,等价于将(3)重写为它的对偶形式(4)。

其中Q(a,π)表示二元化的目标函数,π为(3)中所有对偶变量的向量,Γa,π由约束空间组成。为了更好地演示,问题(4)被进一步修改为一个最小化问题(5),在那里我们以(5a)-(5c)的形式重写了Γa,π。具体来说,(5a)构造了不确定性集,(5b)制定了操作约束,并且(5c)确保了KKT条件的双重可行性。
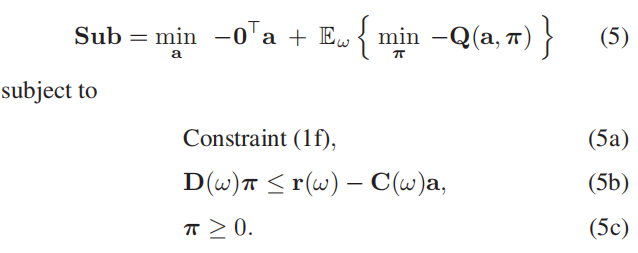
请注意,在目标函数中,Q(a,π)包含了由主问题确定的第一阶段决策x∗。该子问题展现了典型的两阶段随机混合整数双线性最小化结构。此外,线性松弛技术例如Big M方法(见附录A)可以有效地放松双线性部分而不损失准确性。由于整数变量的二进制特性使得凸松弛更加紧密,我们可以确保所得到的解的准确性。根据随机L形法[17],具有线性回应和有限支持的两阶段混合整数随机规划也是可分解的,如下所示。

在l型主问题中,η是一个辅助变量,αo和βo是由l型子问题的对偶计算出来的子梯度,这将在下一小节中讨论。请注意,这个公式是用于单次切割的l形算法的。
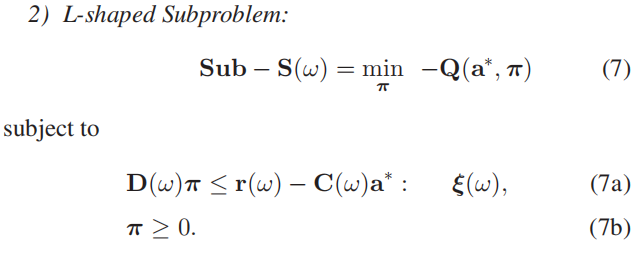
当l形主问题得到一个∗的最优解时,子问题接收到这个解并解决操作问题。设ξ∗(ω)表示运算约束(7a)的最优对偶解。在求解了可以并行完成的ω个单个l形子问题后,每次迭代的子梯度可以计算如下。
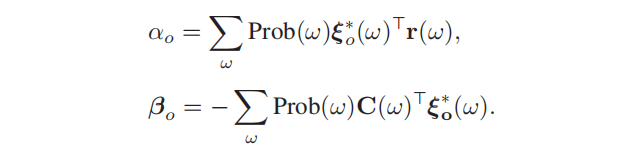
然后,l形主问题得到一个最优性切割(6b)。最后,∗形过程的内部迭代循环确定了最终的最坏情况偶然事件,并将其发送回C&CG主问题。由于我们实现了减负荷,所有问题的可行性都得到了保证,因此可行性削减可以忽略不计。
根据收敛性分析[16]和[17],该算法通过第二阶段随机追索不确定集的有限极值点和有限支持来保证其收敛性。图2显示,C&CG过程不会影响嵌入式L形方法的收敛速度,这意味着我们仍然保持了C&CG方法[16]的快速收敛。C&CG部分的收敛性依赖于L形算法的收敛性,并由随机追索中有限的支持度来保证。根据[4]和[11]的报道,解决原始子问题占据了大部分的计算时间。采用L形方法时,我们利用并行计算的优势来方便解决子问题。
4.算例分析
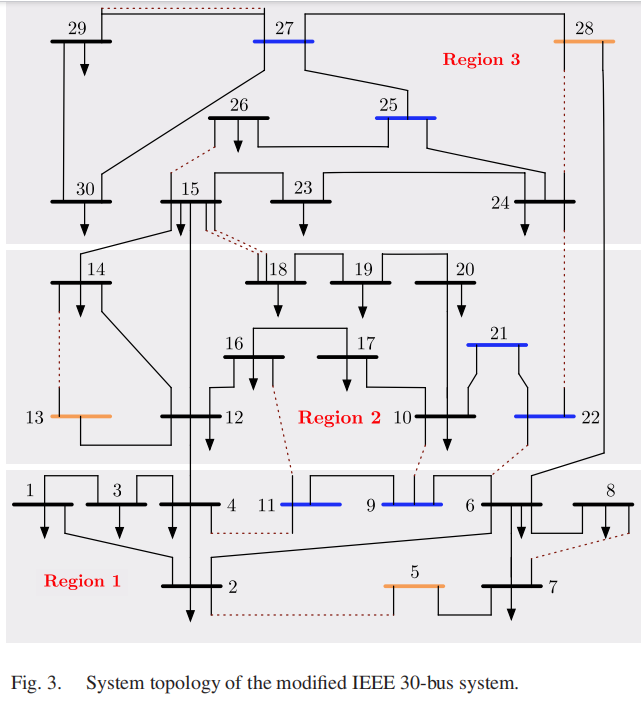
为了说明我们提出的方法,我们修改了IEEE 30节点系统,使其减少传输线路并且没有现有的发电机。图3显示了详细的拓扑结构,其中蓝色和橙色的节点分别表示建设风力发电机和太阳能发电机的候选位置。热力发电机可以投资于任何负荷节点。虚线表示候选输电线路。表格I显示了投资信息,可以在[24]–[26]中找到参考资料。修改后的IEEE 30节点系统每日的峰值功率需求总和为2,000兆瓦,分布在三个地区。我们将负荷削减的惩罚成本设置为1,000美元/兆瓦时。





5.完整代码获取
代码获取链接如下:
https://github.com/thiagojluz/IEEE-Thiago-Luz
相关文章:

开源代码分享(9)—面向100%清洁能源的发输电系统扩展规划(附matlab代码)
1.背景介绍 1.1摘要 本文提出了一种新颖的建模框架和基于分解的解决策略,将随机规划(SP)和鲁棒优化(RO)相结合,以应对协调中长期电力系统规划中的多重不确定性。从独立系统运营商(ISOÿ…...

为 Google Play 即将推出基于区块链的内容政策做好准备
作者 / Joseph Mills, Group Product Manager, Google Play 作为一个平台,Google Play 一直致力于帮助开发者将创新理念变为现实。Google Play 上托管了许多和区块链相关的应用,我们深知合作伙伴们希望扩展这些应用,并利用 NFT 等代币化数字资…...

查找-多路查找详解篇
多路查找树 多路查找树(Multway Search Tree)是一种高级的树形数据结构,它 允许每个节点有多个子节点(通常大于等于2)。多路查找树的每个节点 可以存储多个关键字和对应的值。分类 2-3树(2-3 Tree&#x…...
css设置八等分圆
现需要上图样式的布局,我通过两张向右方的图片,通过定位和旋转完成了布局。 问题: 由于是通过旋转获取到的样式,实际的盒子是一个长方形,当鼠标移入对应的箭头时选中的可能是其他盒子,如第一张设计稿可以看…...

「教程」如何使用一套代码在多种程序中接入天气预警API
引言 天气预警的重要性不言而喻,在遭受自然灾害和极端天气时,及时获得预警信息可以拯救生命和减少财产损失。如今,随着科技的进步,开发者和企业可以借助天气预警 API 这款强大的服务,将实时预警信息集成到自己的应用中…...
(MYSQL)数据库服务端的启动与停止,登录与退出
MYSQL服务的启动与停止 方式一:右击左下角win图标——选择计算机管理——选择计算机管理(本地)——选择服务和应用程序——找到mysql(此方法不好用) 方式二:通过管理员身份运行(必须是管理员身…...

数学建模学习(8):单目标和多目标规划
优化问题描述 优化 优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值 线性规划 线性规划是指目标函数和约束都是线性的情况 [x,fval]linprog(f,A,b,Aeq,Beq,LB,U…...

【Vscode | R | Win】R Markdown转html记录-Win
Rmd文件转html R语言环境Vscode扩展安装及配置配置radian R依赖包pandoc安装配置pandoc环境变量验证是否有效转rmd为html 注意本文代码块均为R语言代码,在R语言环境下执行即可 R语言环境 官网中去下载R语言安装包以及R-tool 可自行搜寻教程 无需下载Rstudio Vscod…...

【Lua语法】字符串操作、字符串中的方法
1.对字符串的操作 --声明一个字符串 str "我是一个字符串"--1.获取字符串的长度 -- 前面加个#即可(注意:Lua中字母占1个长度,汉字占3个长度) print(#str)--2.字符串多行打印 -- 方法1.Lua中是支持转义字符的 print("哈哈\n嘻嘻&q…...

Linux 终端生成二维码
1、安装qrencode [rootnode1 script]# yum -y install qrencode2、输出正常的 [rootnode1 ~]# echo https://www.github.com|qrencode -o - -t utf83、输出彩色的 [rootnode1 ~]# qrencode -t utf8 -s 1 https://www.github.com|lolcatPS:没有lolcat命令 #由于…...
子组件未抛出事件 父组件如何通过$refs监听子组件中数据的变化
我们平时开发项目会使用一些比较成熟的组件库, 但是在极小的情况下,可能会出现我们需要监听某个属性的变化,使我们的页面根据这个属性发生一些改变,但是偏偏组件库没有把这个属性抛出来,当我们使用watch通过refs监听时,由于生命周期的原因还不能拿到,这时候我们可以这样做,以下…...
【C++】STL——stack的介绍和使用、stack的push和pop函数介绍和使用、stack的其他成员函数
文章目录 1.stack的介绍2.stack的使用2.1stack构造函数2.1stack成员函数(1)empty() 检测stack是否为空(2)size() 返回stack中元素的个数(3)top() 返回栈顶元素的引用(4)push() 将元素…...
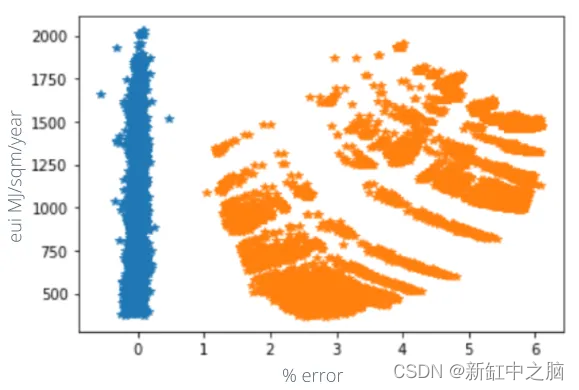
基于BIM+AI的建筑能源优化模型【神经网络】
推荐:用 NSDT设计器 快速搭建可编程3D场景。 AEC(建筑、工程、施工)行业的BIM 技术,允许在实际施工开始之前虚拟地建造建筑物; 这带来了许多有形和无形的好处:减少成本超支、更有效的协调、增强决策权等等。…...

#P0998. [NOIP2007普及组] 守望者的逃离
题目背景 恶魔猎手尤迪安野心勃勃,他背叛了暗夜精灵,率领深藏在海底的娜迦族企图叛变。 题目描述 守望者在与尤迪安的交锋中遭遇了围杀,被困在一个荒芜的大岛上。 为了杀死守望者,尤迪安开始对这个荒岛施咒,这座岛…...
vue3+ts+elementui-plus二次封装弹框
一、弹框组件BaseDialog <template><div classmain><el-dialog v-model"visible" :title"title" :width"dialogWidth" :before-close"handleClose"><!-- 内容插槽 --><slot></slot><template…...

ffmpeg批量分割视频解决视频前几秒黑屏的问题解决
echo 请输入视频地址: set /p fp echo 请输入开始时间: set /p st echo 请输入结束时间: set /p et echo 请输入分片时间: set /p sgt echo 注意:循环范围参数要空格。 for /l %%i in (%st%, %sgt%, %et%) do call :aa…...

nodejs + express 调用本地 python程序
假设已经安装好 nodejs ; cd /js/node_js ; 安装在当前目录的 node_modules/ npm install express --save 或者 cnpm install express --save web 服务器程序 server.js const http require(http); const express require(express); const path require(path); const …...

微信小程序代码优化3个小技巧
抽取重复样式 样式复用 我们会发现很多时候在开发的过程中会存在多个页面中都用到了同样的样式,那么其实之前有提到过,公用样式可以放在app.wxss里面这样就可以直接复用。 如:flex布局的纵向排列,定义在app.wxss里面 .flex-co…...
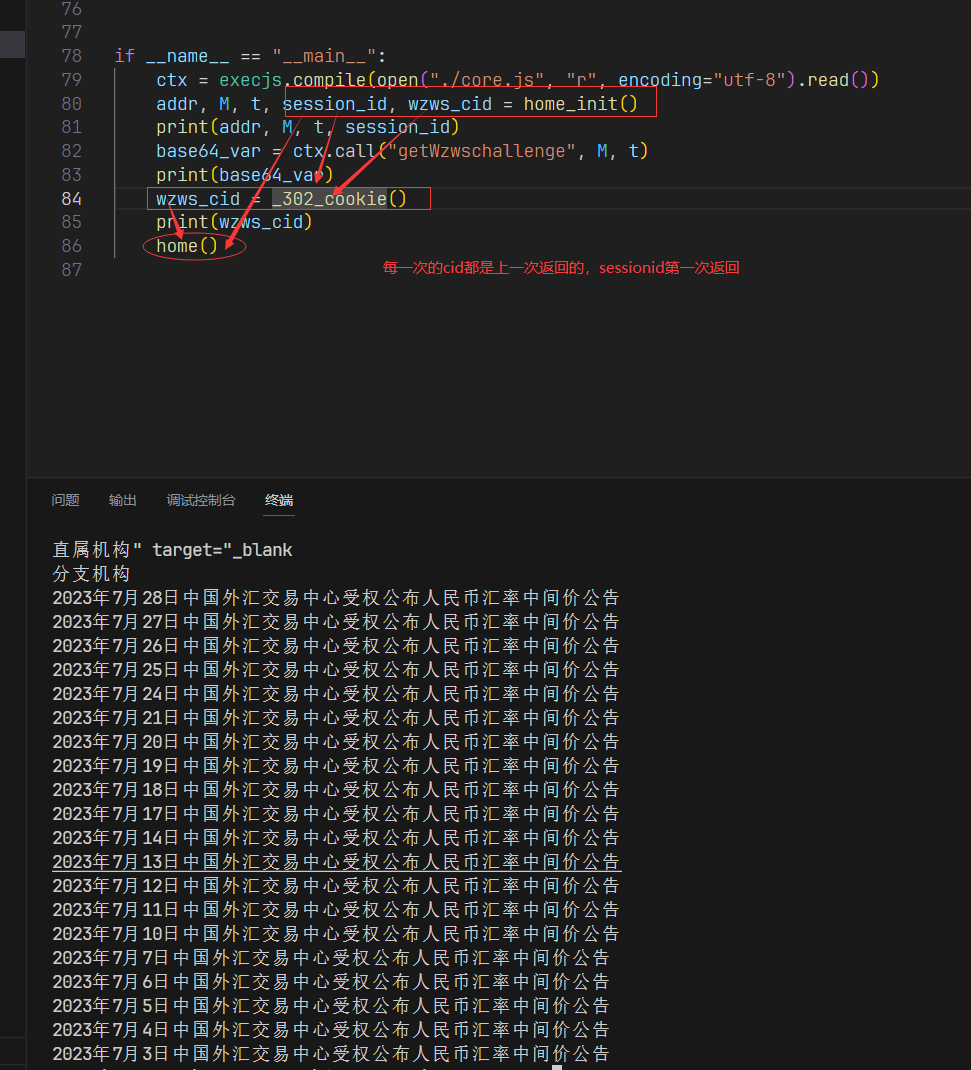
某行动态cookie反爬虫分析
某行动态cookie反爬虫分析 1. 预览 反爬网址(base64): aHR0cDovL3d3dy5wYmMuZ292LmNu 反爬截图: 需要先加载运行js代码,可能是对环境进行检测,反调试之类的 无限debugger 处理办法 网上大部分人说的都是添加cookie来解决。 那个noscript…...

恒运资本:A股、港股全线爆发,沪指突破3300点,恒指重返2万点上方
7月31日,两市股指高开高走,沪指在金融、地产、酿酒等权重板块的带动下一举突破3300点。截至发稿,沪指、深成指、创业板指涨幅均超1%,上证50指数涨近2%。Wind数据显现,北向资金净买入超25亿元。 职业方面,券…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
