【数据结构篇C++实现】- 图
友情链接:C/C++系列系统学习目录
文章目录
- 🚀一、图的基本概念和术语
- 1、有向图和无向图
- 3、基本图和多重图
- 4、完全图
- 5、子图
- 6、连通、连通图和连通分量
- 7、强连通图、强连通分量
- 8、生成树、生成森林
- 9、顶点的度、入度和出度
- 10、边的权和网
- 11、稠密图、稀疏图
- 12、路径、路径长度和回路
- 13、 简单路径、简单回路
- 14、距离
- 15、有向树
- 🚀二、图的表示:邻接表
- ⛳(一)邻接列表原理精讲
- ⛳(二)邻接表的算法实现
- 1.邻接表结构的定义
- 2.邻接表的初始化
- 3.邻接表的创建
- 🚀三、邻接表的深度遍历
- ⛳(一)深度优先遍历算法原理
- ⛳(二)深度优先遍历算法实现
- 🚀四、邻接表的广度遍历
- ⛳(一)广度优先遍历算法原理
- ⛳(二)广度优先遍历算法实现
- 程序清单
🚀一、图的基本概念和术语
**概念:**在计算机科学中,一个图就是一些顶点的集合,这些顶点通过一系列边结对(连接)。顶点用圆圈表示,边就是这些圆圈之间的连线。顶点之间通过边连接。注意:顶点有时也称为节点或者交点,边有时也称为链接。 社交网络,每一个人就是一个顶点,互相认识的人之间通过边联系在一起, 边表示彼此的关系。这种关系可以是单向的,也可以是双向的!
树和链表都是图的特例,在线性表中,数据元素之间是被串起来的,仅有线性关系,每个数据元素只有一个直接前驱和一个直接后继。在树形结构中,数据元素之间有着明显的层次关系,并且每一层上的数据元素可能和下一层中多个元素相关,但只能和上一层中一个元素相关。图是一种较线性表和树更加复杂的数据结构。在图形结构中,结点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。
如果一个编程问题可以通过顶点和边表示,那么我们就可以将问题用图画出来,然后使用相应的算法来找到解决方案
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pJ0nLt8L-1690729858577)(E:\create\图片\图\1.png)]
1、有向图和无向图

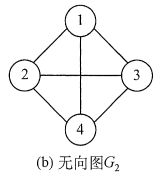
3、基本图和多重图
一个图G若满足:①不存在重复边;②不存在顶点到自身的边,则称图G为简单图。上图中G1 和G2 均为简单图。数据结构中仅讨论简单图。
若图G中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联,则G为多重图。多重图的定义和简单图是相对的。
4、完全图
对于无向图,在完全图中任意两个顶点之间都存在边。
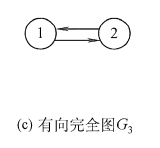
对于有向图,在有向完全图中任意两个顶点之间都存在方向相反的两条弧。
上图中G2为无向完全图,而G3为有向完全图。
5、子图
上图中G3为G1的子图。
6、连通、连通图和连通分量
在无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的。若图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。无向图中的极大连通子图称为连通分量。若一个图有n个顶点,并且边数小于n − 1,则此图必是非连通图。如下图(a)所示, 图G4有3个连通分量,如图(b)所示。
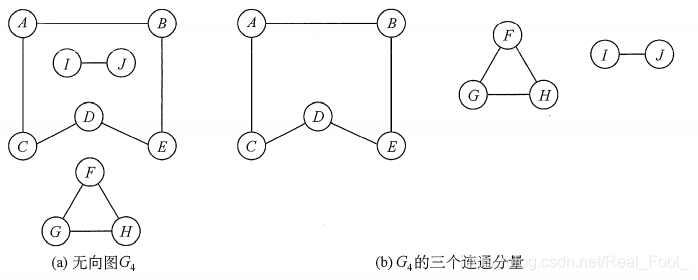
注意:弄清连通、连通图、连通分量的概念非常重要。首先要区分极大连通子图和极小连通子图,极大连通子图是无向图的连通分量,极大即要求该连通子图包含其所有的边;极小连通子图是既要保持图连通又要使得边数最少的子图。
7、强连通图、强连通分量
在有向图中,若从顶点v到顶点w和从顶点w到项点v之间都有路径,则称这两个顶点是强连通的。若图中任何一对顶点都是强连通的,则称此图为强连通图。有向图中的极大强连通子图称为有向图的强连通分量,图G1的强连通分量如下图所示。
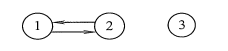
注意:强连通图、强连通分量只是针对有向图而言的。一般在无向图中讨论连通性,在有向图中考虑强连通性。
8、生成树、生成森林
连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为n,则它的生成树含有n − 1条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。在非连通图中,连通分量的生成树构成了非连通图的生成森林。图G2的一个生成树如下图所示。
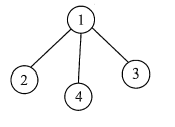
注意:包含无向图中全部顶点的极小连通子图,只有生成树满足条件,因为砍去生成树的任一条边,图将不再连通。
9、顶点的度、入度和出度
图中每个顶点的度定义为以该项点为一个端点的边的数目。
对于有向图,顶点v vv的度分为入度和出度,入度就是进来的边,出度就是出去的边
10、边的权和网
在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。这种边上带有权值的图称为带权图,也称网。
11、稠密图、稀疏图
边数很少的图称为稀疏图,反之称为稠密图。稀疏和稠密本身是模糊的概念,稀疏图和稠密图常常是相对而言的。
12、路径、路径长度和回路
顶点vp到顶点vq之间的一条路径是指它们之间的顶点序列(包括本身),当然关联的边也可以理解为路径的构成要素。路径上边的数目称为路径长度。第一个顶点和最后一个顶点相同的路径称为回路或环。若一个图有n个顶点,并且有大于n − 1条边,则此图一定有环。
13、 简单路径、简单回路
在路径序列中,顶点不重复出现的路径称为简单路径。除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。
14、距离
从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离。若从u到v根本不存在路径,则记该距离为无穷( ∞ )。
15、有向树
一个顶点的入度为0、其余顶点的入度均为1的有向图,称为有向树。
🚀二、图的表示:邻接表
⛳(一)邻接列表原理精讲
- 在邻接列表实现中,每一个顶点会存储一个从它这里开始的相邻边的列表。比如,如果顶点 B 有一条边到 A、C 和 E,那么 B 的列表中会有 3 条边。
- 邻接列表只描述指向外部的边。B 有一条边到 A,但是 A 没有边到 B,所以 B 没有出现在 A 的邻接列表中。
- 查找两个顶点之间的边或者权重会比较费时,因为要遍历邻接列表直到找到为止。
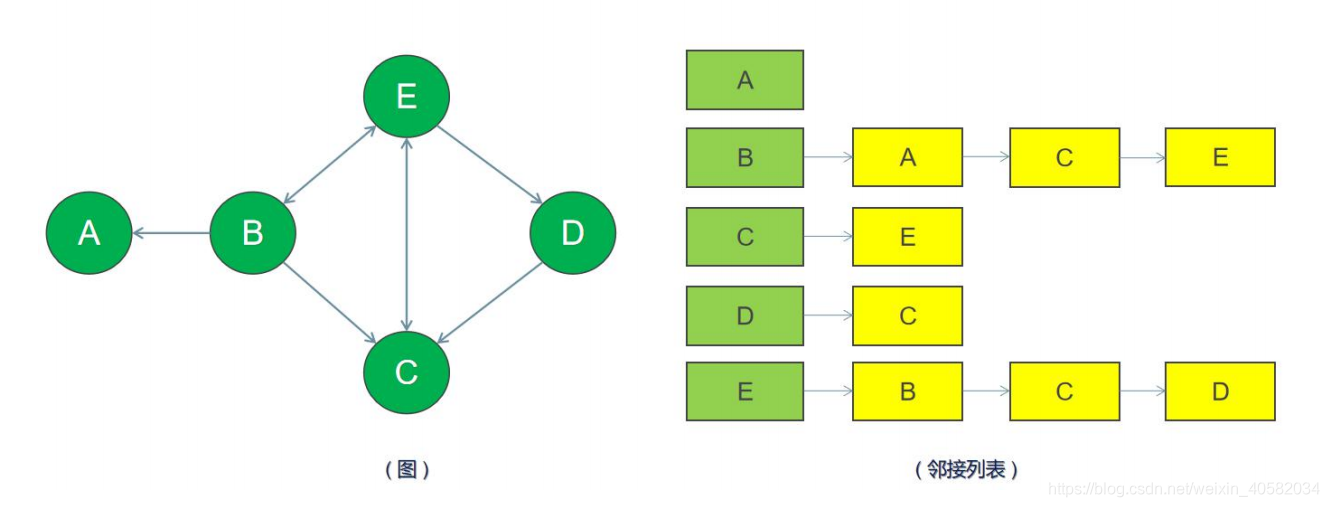
邻接矩阵:
由二维数组对应的行和列都表示顶点,由两个顶点所决定的矩阵对应元素数值表示这里两个顶点是否相连(如,0表示不相连,非0表示相连和权值)﹑如果相连这个值表示的是相连边的权重。例如,广西到北京的机票,我们用邻接矩阵表示:
- 行表示起点,列表示终点
- 往这个图中添加顶点的成本非常昂贵,因为新的矩阵结果必须重新按照新的行/列创建,然后将已有的数据复制到新的矩阵中。
- 即用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YNpfMlMW-1690729858579)(E:\create\图片\图\2.png)]
#define MaxVertexNum 100 //顶点数目的最大值 typedef char VertexType; //顶点的数据类型 typedef int EdgeType; //带权图中边上权值的数据类型 typedef struct{VertexType Vex[MaxVertexNum]; //顶点表EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表int vexnum, arcnum; //图的当前顶点数和弧树 }MGraph;比较:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OjUq1hBo-1690729858580)(E:\create\图片\图\3.png)]
结论:大多数时候,选择邻接列表是正确的。(在图比较稀疏的情况下,每一个顶点都只会和少数几个顶点相连,这种情况下邻接列表是最佳选择。如果这个图比较密集,每一个顶点都和大多数其他顶点相连,那么邻接矩阵更合适。)
⛳(二)邻接表的算法实现

顶点表结点由顶点域(data)和指向第一条邻接边的指针(firstarc) 构成,边表(邻接表)结点由邻接点域(adjvex)和指向下一条邻接边的指针域(nextarc) 构成。
1.邻接表结构的定义
#define MAXSIZE 1024typedef struct _EdgeNode//新的边
{int adjvex;//邻接的顶点 (用下标位置来表示)int weight;//权重struct _EdgeNode *next;//指向下一个顶点/边
}EdgeNode;typedef struct _VertexNode//顶点结点
{char data;//结点数据struct _EdgeNode *first; //指向邻接的第一条边
}VertexNode,*AdjList;typedef struct _AdJListGraph
{AdjList adjList;//顶点数组,结构体数组int numVex;int numEdg;
}AdjListGraph;
2.邻接表的初始化
bool Init(AdjListGraph &gh)
{gh.adjList = new VertexNode[MAXSIZE];//分配顶点数组地址if (!gh.adjList) return false;gh.numEdg = 0;gh.numVex = 0;}

3.邻接表的创建
//寻找顶点的数据找到数组的下标
int Location(AdjListGraph gh, char c)
{if (gh.numVex <= 0) return -1;for (int i=0;i<gh.numVex;i++){if (c==gh.adjList[i].data){return i;}}return-1;
}//图的创建
void CreateALGraph(AdjListGraph &gh)
{cout << "输入图的定点数 和边数:";cin >> gh.numVex >> gh.numEdg;if (gh.numVex > MAXSIZE) return;cout << endl << "输入相关顶点: " << endl;//保存顶点for (int i=0;i<gh.numVex;i++){cin >> gh.adjList[i].data;gh.adjList[i].first = NULL; //顶点的第一条边目前连接为空}char vi, vj;//保存输入的顶点;int i, j;cout << "请依次输入边(vi,vj)上的顶点序号:" << endl;for(int k = 0; k < gh.numEdg; k++){cin >> vi >> vj;i = Location(gh, vi); //获取要连接的两个点在数组中的下标j = Location(gh, vj);if (i>=0 && j>=0){ //头插法插入边EdgeNode *temp = new EdgeNode; temp->adjvex = j; temp->next = gh.adjList[i].first;gh.adjList[i].first = temp;}}
}

🚀三、邻接表的深度遍历
⛳(一)深度优先遍历算法原理
首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点;
当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直到所有的顶点都被访问过。
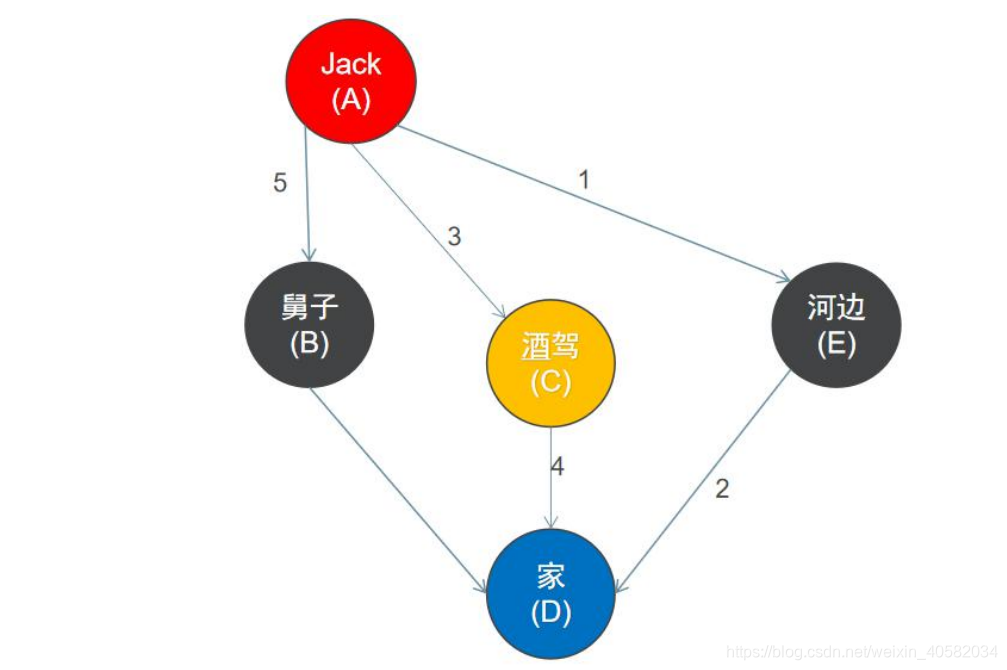
使用深度优先搜索来遍历这个图的具体过程是:
- 首先从一个未走到过的顶点作为起始顶点,比如 A 顶点作为起点。
- 沿 A 顶点的边去尝试访问其它未走到过的顶点,首先发现 E 号顶点还没有走到过,于是访问 E 顶点。
- 再以 E 顶点作为出发点继续尝试访问其它未走到过的顶点,接下来访问 D 顶点。
- 再尝试以 D 顶点作为出发点继续尝试访问其它未走到过的顶点。
- 但是,此时沿 D 顶点的边,已经不能访问到其它未走到过的顶点,接下来返回到 E 顶点。
- 返回到 E 顶点后,发现沿 E 顶点的边也不能再访问到其它未走到过的顶点。此时又回到顶点 A( D-> E-> A),再以 A 顶点作为出发点继续访问其它未走到过的顶点,于是接下来访问 C 点。
- 以此类推
- 最终访问的结果是 A -> E -> D -> C -> B
⛳(二)深度优先遍历算法实现
bool visited[MAXSIZE] = {0};//全局数据用来判断元素是否被访问过//对图上的顶点进行深度遍历
void DFS(adjListGraph &gh,int i)
{int nextNum = -1;if (visited[i])//如果该结点已经被访问则返回 return;//访问该结点cout << gh.adjList[i].data << " ";visited[i] = true;EdgeNode *tmp = gh.adjList[i].first;while (tmp){nextNum = tmp->adjvex;if (visited[nextNum]==false){DFS(gh, nextNum);}tmp = tmp->next;}}//对所有顶点进行深度遍历
void DFS_All(AdjListGraph &gh)
{for (int i=0;i<gh.numVex;i++){if (visited[i]==false){DFS(gh, i);}}
}
🚀四、邻接表的广度遍历
⛳(一)广度优先遍历算法原理
首先以一个未被访问过的顶点作为起始顶点,访问其所有相邻的顶点;
然后对每个相邻的顶点,再访问它们相邻的未被访问过的顶点,直到所有顶点都被访问过,遍历结束。

⛳(二)广度优先遍历算法实现
//对图上的顶点进行广度遍历
void BFS(AdjListGraph &gh,int i)
{int cur = -1;queue<int> q;q.push(i);while (!q.empty())//队列不为空{cur = q.front();//取队列的头元素if (visited[cur]==false){cout << gh.adjList[cur].data << " ";visited[cur] = true;}q.pop();//取当前结点相邻的结点入队EdgeNode *tmp = gh.adjList[cur].first;while (tmp!=NULL){q.push(tmp->adjvex);tmp = tmp->next;}}
}
//对所有顶点进行广度遍历
void BFS_All(AdjListGraph &gh)
{for (int i = 0; i < gh.numVex; i++){if (visited[i] == false){BFS(gh, i);}}
}
程序清单
#include <iostream>
#include <queue>
#define MAXSIZE 1024
using namespace std;typedef struct _EdgeNode//与结点连接的边
{int adjvex;//邻接的顶点 int weight;//权重struct _EdgeNode *next;//指向下一个顶点/边
}EdgeNode;typedef struct _VertexNode//顶点结点
{char data;//结点数据struct _EdgeNode *first;
}VertexNode,*AdjList;typedef struct _AdJListGraph
{AdjList adjList;//顶点数组int numVex;int numEdg;
}AdjListGraph;//图的初始化
bool Init(AdjListGraph &gh)
{gh.adjList = new VertexNode[MAXSIZE];//分配顶点数组地址if (!gh.adjList) return false;gh.numEdg = 0;gh.numVex = 0;}//寻找顶点的数据找到数组的下标
int Location(AdjListGraph gh, char c)
{if (gh.numVex <= 0) return -1;for (int i=0;i<gh.numVex;i++){if (c==gh.adjList[i].data){return i;}}return-1;
}//图的创建
void CreateALGraph(AdjListGraph &gh)
{cout << "输入图的定点数 和边数:";cin >> gh.numVex >> gh.numEdg;if (gh.numVex > MAXSIZE) return;cout << endl << "输入相关顶点: " << endl;//保存顶点for (int i=0;i<gh.numVex;i++){cin >> gh.adjList[i].data;gh.adjList[i].first = NULL;}char vi, vj;//保存输入的顶点;int i, j;cout << "请依次输入边(vi,vj)上的顶点序号:" << endl;for(int k = 0; k < gh.numEdg; k++){cin >> vi >> vj;i = Location(gh, vi);j = Location(gh, vj);if (i>=0 && j>=0){EdgeNode *temp = new EdgeNode;temp->adjvex = j;temp->next = gh.adjList[i].first;gh.adjList[i].first = temp;}}
}bool visited[MAXSIZE] = {0};//全局数据用来判断元素是否被访问过//对图上的顶点进行深度遍历
void DFS(AdjListGraph &gh,int i)
{int nextNum = -1;if (visited[i])//如果该结点已经被访问则返回 return;//访问该结点cout << gh.adjList[i].data << " ";visited[i] = true;EdgeNode *tmp = gh.adjList[i].first;while (tmp){nextNum = tmp->adjvex;if (visited[nextNum]==false){DFS(gh, nextNum);}tmp = tmp->next;}}//对所有顶点进行深度遍历
void DFS_All(AdjListGraph &gh)
{for (int i=0;i<gh.numVex;i++){if (visited[i]==false){DFS(gh, i);}}
}//对图上的顶点进行广度遍历
void BFS(AdjListGraph &gh,int i)
{int cur = -1;queue<int> q;q.push(i);while (!q.empty())//队列不为空{cur = q.front();//取队列的头元素if (visited[cur]==false){cout << gh.adjList[cur].data << " ";visited[cur] = true;}q.pop();//取当前结点相邻的结点入队EdgeNode *tmp = gh.adjList[cur].first;while (tmp!=NULL){q.push(tmp->adjvex);tmp = tmp->next;}}
}
//对所有顶点进行广度遍历
void BFS_All(AdjListGraph &gh)
{for (int i = 0; i < gh.numVex; i++){if (visited[i] == false){BFS(gh, i);}}
}
int main()
{AdjListGraph G;cout << "正在创建邻接表,请按提示进行输入..." << endl;Init(G);CreateALGraph(G);cout << "正在进行深度优先遍历,遍历结果如下:" << endl;//深度优先遍历DFS_All(G);cout << endl;memset(visited, 0, sizeof(visited));cout << "正在进行广度优先遍历,遍历结果如下:" << endl;//广度优先遍历BFS_All(G);cout << endl;
}
相关文章:

【数据结构篇C++实现】- 图
友情链接:C/C系列系统学习目录 文章目录 🚀一、图的基本概念和术语1、有向图和无向图3、基本图和多重图4、完全图5、子图6、连通、连通图和连通分量7、强连通图、强连通分量8、生成树、生成森林9、顶点的度、入度和出度10、边的权和网11、稠密图、稀疏图…...

Sentinel持久化规则
项目中有用到Sentinel,然后需要将Sentinel上配置的规则做持久化(或者初始化),通过改写Sentinel源码实现了需求,下面记录一下实现过程。 如果不知道Sentinel怎么搭,可以看看: 流控平台Sentinel搭建和接入教程_东皋长歌的博客-CSDN博客 一,背景 Sentinel是Alibaba开源…...
list与sort()
运行代码: //list与sort() #include"std_lib_facilities.h" //声明Item类 struct Item {string name;int iid;double value;Item():name(" "),iid(0),value(0.0){}Item(string ss,int ii,double vv):name(ss),iid(ii),value(vv){}friend istre…...

6个月、21天,GoldenDB分布式数据库核心系统落地中移动
近日,2023“鼎新杯”数字化转型应用大赛入围名单公示,山东移动基于GoldenDB分布式数据库的CRM&BOSS核心系统自主创新实践成功入选。该项目是中兴通讯与中国移动在数据库关键领域的又一个合作范例。 核心系统业务量大,分布式转型迫在眉睫 …...
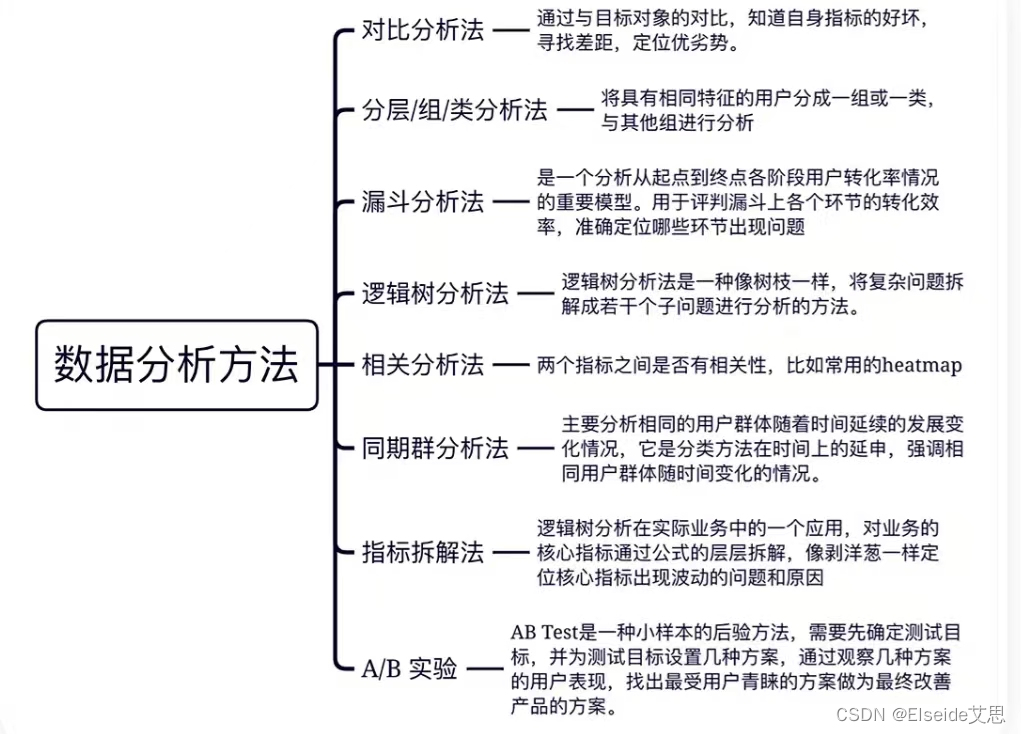
如何正确培养数据思维?
在大数据时代,数据思维已成了每个人的必备品。下面,我们就来了解一下,什么是数据思维。不过要想弄懂什么是数据思维,首先来打破大家对数据的错误认知,数据不仅仅指数字。 1. 数据思维是什么? 百度百科对数…...

JavaScript中的?.和??的用法
1、?.(可选链运算符) 在JavaScript中,"?.“是一种叫做"Optional Chaining”(可选链)的新操作符。它允许我们在访问一个可能为null或undefined的属性或调用一个可能不存在的方法时,避免出现错误…...

Git for linux
<1> linux 安装git sudo apt-get install git-all <2> 创建git,分为两部分,远程网络部分和本地主机部分 远程网路:登录GitHub: Let’s build from here GitHub 注册帐号,创建登录密码,此密码很长&a…...
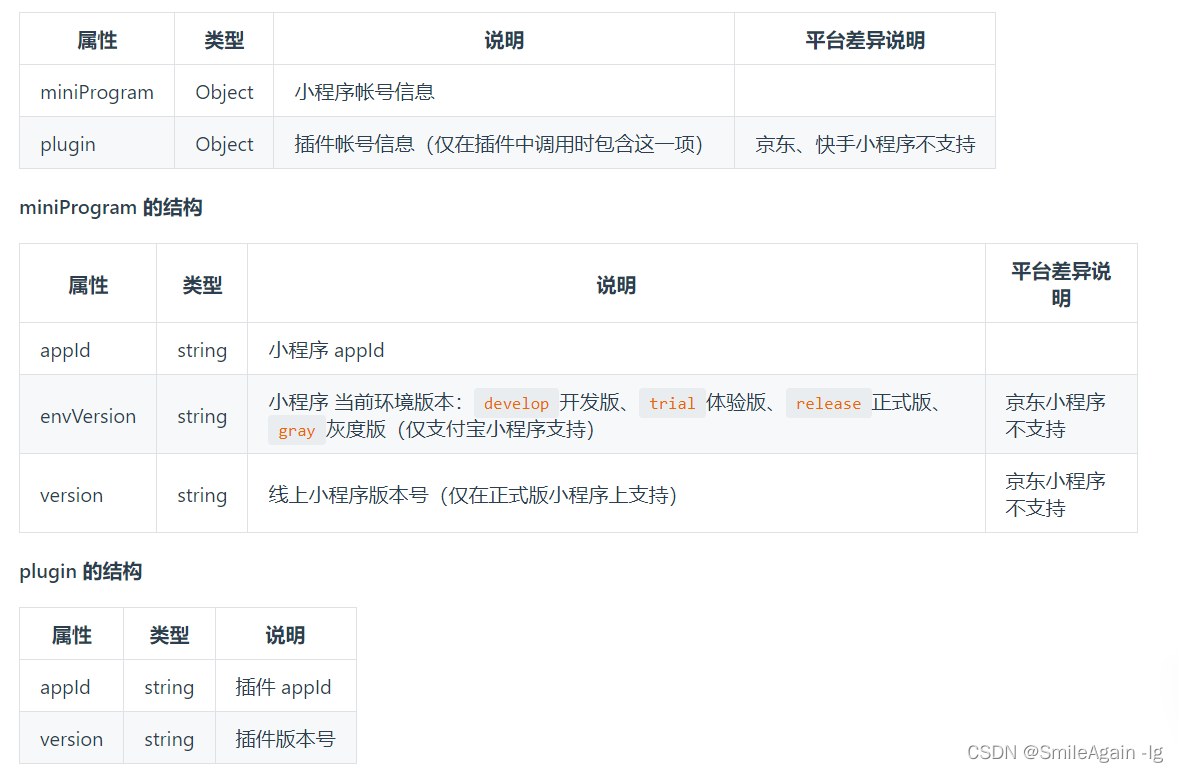
uniapp小程序,根据小程序的环境版本,控制的显页面功能按钮的示隐藏
需求:根据小程序环境控制控制页面某个功能按钮的显示隐藏; 下面是官方文档和功能实现的相关代码: 实现上面需要,用到了uni.getAccountInfoSync(): uni.getAccountInfoSync() 是一个 Uniapp 提供的同步方法,…...

kotlin 编写一个简单的天气预报app(二)增加搜索城市功能
增加界面显示openweathermap返回的信息。 在activity_main.xml里增加输入框来输入城市,在输入款旁边增加搜索按钮来进行查询。 然后原来显示helloworld的TextView用来显示结果。 1. 增加输入城市名字的EditText <EditTextandroid:id"id/editTextCity"…...

【分布鲁棒、状态估计】分布式鲁棒优化电力系统状态估计研究[几种算法进行比较](Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

vue中的require
vue中的require 一、基本概念二、具体演示1.引入json2.引入图片 三、require.context引入图片:引入json引入模块js:引入vue文件: 一、基本概念 require 是 node 中的一个方法,他的作用是 用于引入模块、 JSON、或本地静态文件。r…...

Linux进程间共享内存通信时如何同步?(附源码)
今天我们来讲讲进程间使用共享内存通信时为了确保数据的正确,如何进行同步? 在Linux中,进程间的共享内存通信需要通过同步机制来保证数据的正确性和一致性,常用的同步机制包括信号量、互斥锁、条件变量等。 其中,使用信号量来同…...
)
spring注解驱动开发(二)
17、Bean的生命周期 bean的生命周期:bean的创建—初始化—销毁的过程 容器负责管理bean的生命周期 我们可以自定义初始化和销毁方法,容器在bean进行到当前生命周期的时候来调用我们自定义的初始化和销毁方法 构造(对象创建) 单…...

【C++】——类和对象
目录 面向过程和面向对象的初步认识类的引入类的定义类的访问限定符及封装类的作用域类的实例化this指针类的6个默认成员函数构造函数析构函数 面向过程和面向对象的初步认识 C语言是面向过程的,关注的是过程,分析求解问题的步骤,通过函数调用…...

【Docker】使用docker-maven-plugin插件构建发布推镜像到私有仓库
文章目录 1. 用docker-maven-plugin插件推送项目到私服docker1.1. 构建镜像 v1.01.2. 构建镜像 v2.01.3. 推送到镜像仓库 2. 拉取私服docker镜像运行3. 参考资料 本文描述了在Spring Boot项目中通过docker-maven-plugin插件把项目推送到私有docker仓库中,随后拉取仓…...
区块链学习笔记
区块链技术与应用 数组 列表 二叉树 哈希函数 BTC中的密码学原理 cryptographic hash function collsion resistance(碰撞抵抗) 碰撞指的是找到两个不同的输入值,使得它们的哈希值相同。也就是说,如果存在任意两个输入x和y,满足x ≠ y…...
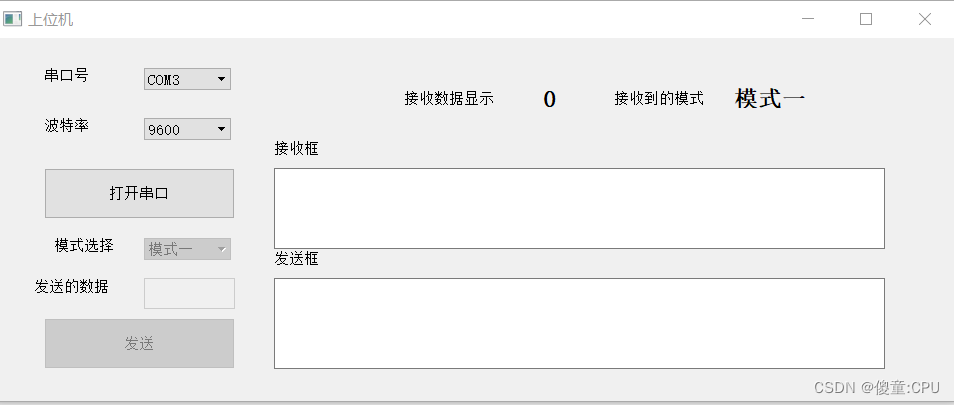
实用上位机--QT
实用上位机–QT 通信协议如下 上位机设计界面 #------------------------------------------------- # # Project created by QtCreator 2023-07-29T21:22:32 # #-------------------------------------------------QT += core gui serialportgreaterThan(QT_MAJOR_V…...

os.signal golang中的信号处理
在程序进行重启等操作时,我们需要让程序完成一些重要的任务之后,优雅地退出,Golang为我们提供了signal包,实现信号处理机制,允许Go 程序与传入的信号进行交互。 Go语言标准库中signal包的核心功能主要包含以下几个方面…...
Python源码:Tkinter组件布局管理的3种方式
Tkinter组件布局管理可以使用pack()方法、grid()方法和place()方法。pack()方法将组件放置在窗口中,grid()方法将组件放置在网格布局中,place()方法将组件放置在指定位置。 01使用pack()方法布局: 在Tkinter中,pack方法用于将控…...
网络防御之VPN
配置IKE 第一阶段 [r1]ike proposal 1 [r1-ike-proposal-1]encryption-algorithm aes-cbc-128 [r1-ike-proposal-1]authentication-algorithm sha1 [r1-ike-proposal-1]dh group2 [r1-ike-proposal-1]authentication-method pre-share[r1]ike peer aaa v1 [r1-ike-peer-aaa…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
