使用Spring Boot AOP实现日志记录
目录
介绍
1.1 什么是AOP
1.2 AOP体系与概念
AOP简单实现
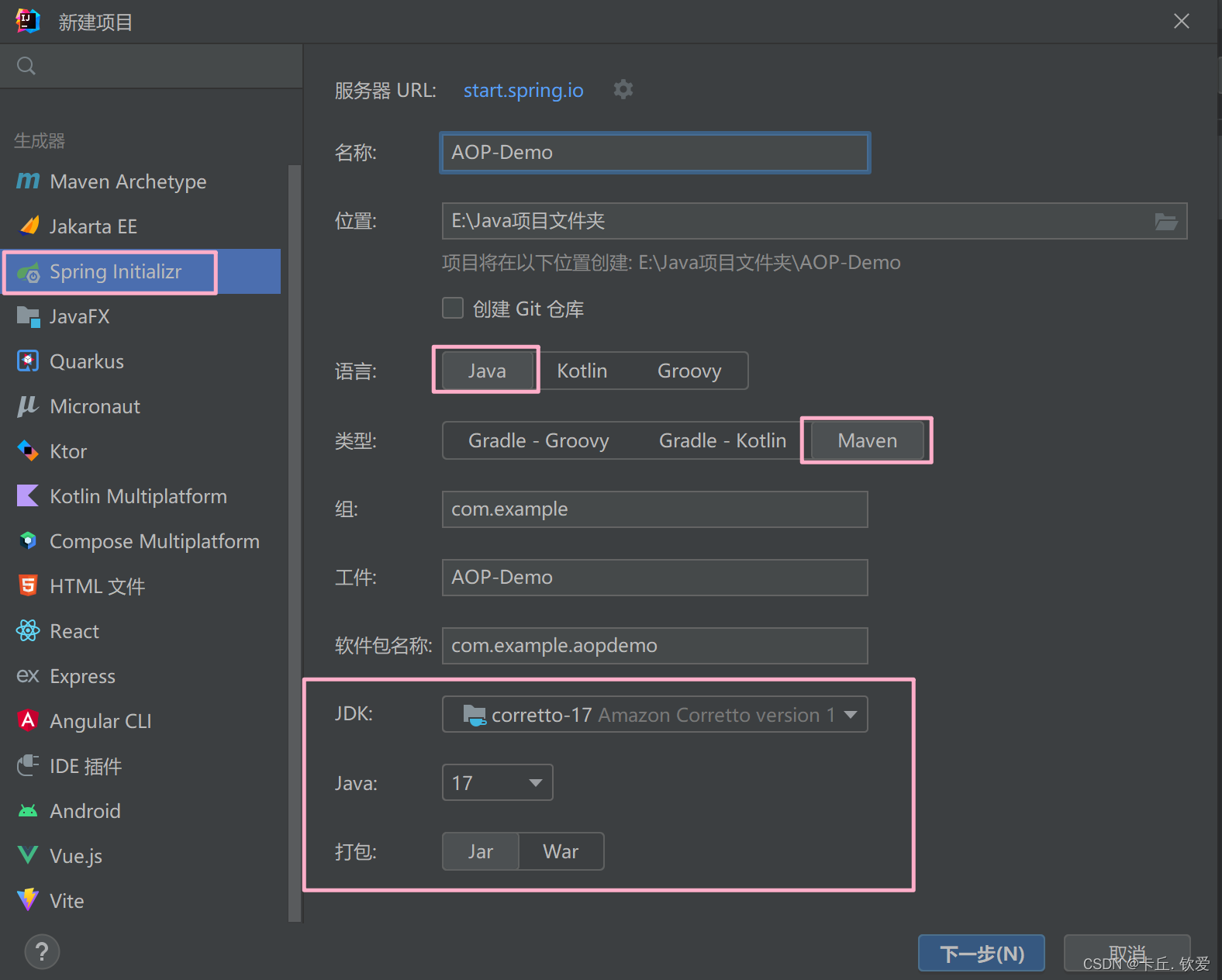
2.1 新建一个SpringBoot项目,无需选择依赖
2.2 设置好本地Maven配置后,在pom.xml文件里添加添加maven依赖
2.3 创建一个业务类接口
2.4 在实体类实现接口业务
2.5 在单元测试运行结果
2.6 创建切面类
2.7 再次运行测试
总结
介绍
1.1 什么是AOP
AOP(Aspect Oriented Programming),面向切面思想,是Spring的三大核心思想之一(两外两个:IOC-控制反转、DI-依赖注入)。
那么AOP为何那么重要呢?
在我们的程序中,经常存在一些系统性的需求,比如权限校验、日志记录、统计等,这些代码会散落穿插在各个业务逻辑中,例如下面这个示意图:
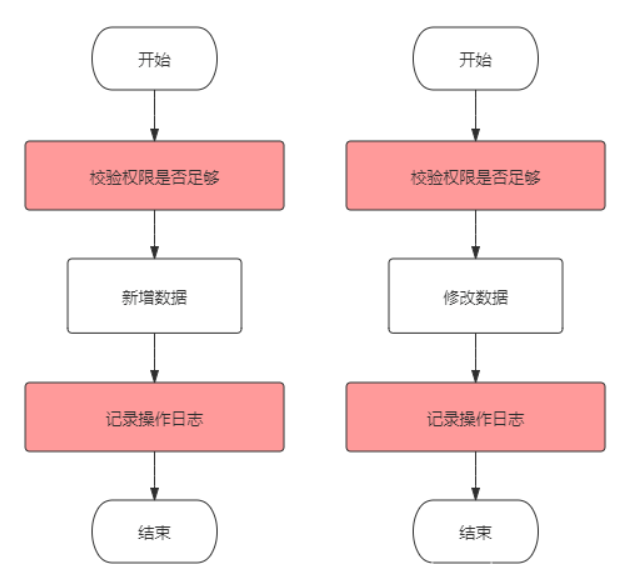
有多少业务操作,就要写多少重复的校验和日志记录代码,这显然是无法接受的。当然,用面向对象的思想,我们可以把这些重复的代码抽离出来,写成公共方法,就是下面这样:
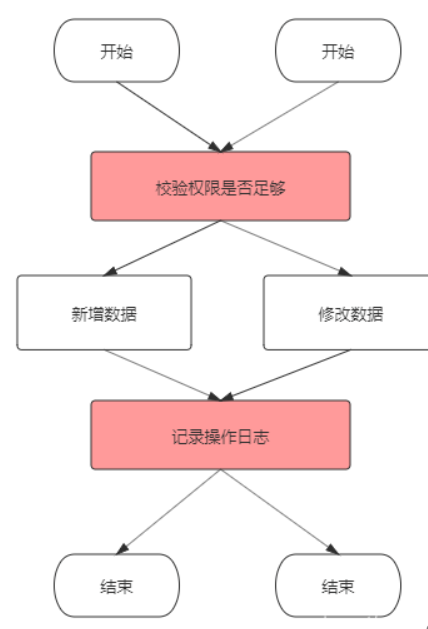
这样,代码冗余和可维护性的问题得到了解决,但每个业务方法中依然要依次手动调用这些公共方法,也是略显繁琐。有没有更好的方式呢?有的,为了解决这个问题,面向切面编程(AOP)应运而生。AOP将权限校验、日志记录等非业务代码完全提取出来,与业务代码分离,并寻找节点切入业务代码中:
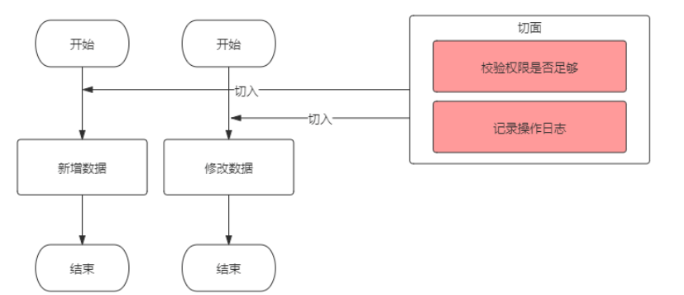
AOP通过预编译方式和运行动态代理实现程序功能的统一维护,AOP是OOP的延续,是软件开发中的一个热点,也是Spring框架中的一个重要内容,是函数式编程的一种衍生泛型。利用AOP可以对业务逻辑的各部分进行隔离,是开发人员在编写业务逻辑时,专注核心业务,从而降低业务逻辑各模块之间的耦合度,提高代码重用和开发效率。
AOP使用横向抽取机制,取代纵向集成体系的重复代码建设。使用Aspect,使业务逻辑只关注业务本身,将日志管理、事务处理、性能统计、异常处理、权限控制等代码从业务逻辑代码中抽离,从而实现改变这些行为的时候不影响业务逻辑代码。
1.2 AOP体系与概念
Spring AOP和AspectJ
目前流行的AOP框架分别为Spring AOP和AspectJ。

AOP相关术语

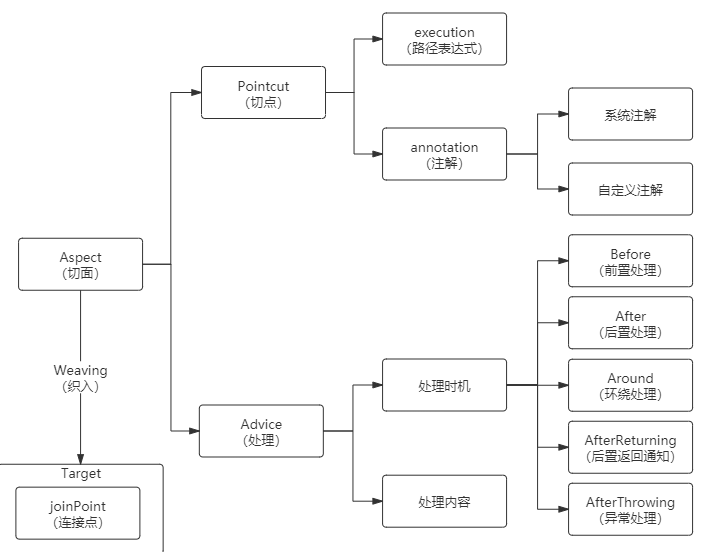
简单地去理解,其实AOP要做三类事:
-
在哪里切入,也就是权限校验等非业务操作在哪些业务代码中执行。
-
在什么时候切入,是业务代码执行前还是执行后。
-
切入后做什么事,比如做权限校验、日志记录等。
因此,AOP的体系可以梳理为下图:
AOP简单实现
下面我们通过一个简单的案例来演示一下AOP的初级应用:
2.1 新建一个SpringBoot项目,无需选择依赖
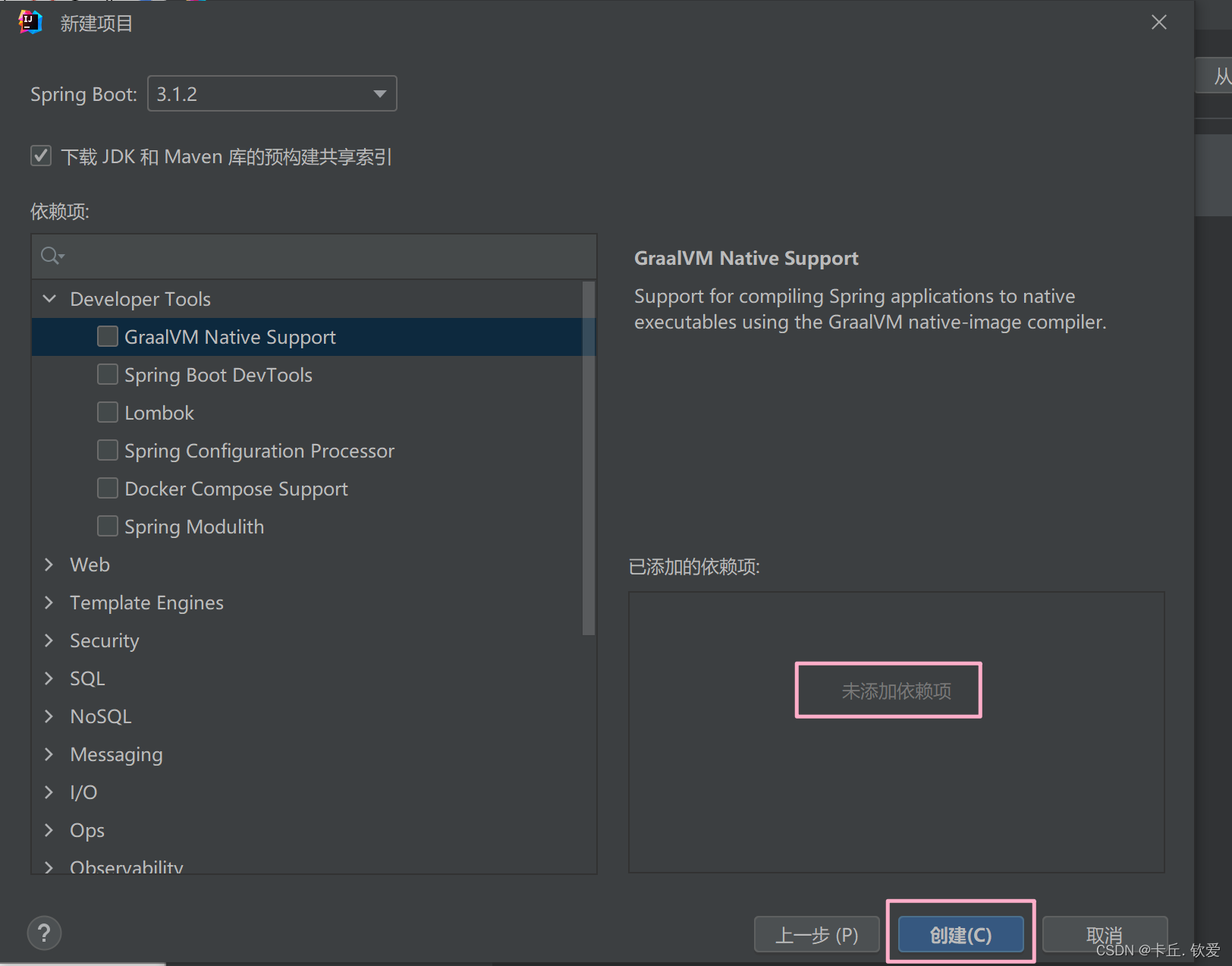
2.2 设置好本地Maven配置后,在pom.xml文件里添加添加maven依赖
<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-aop</artifactId>
</dependency>2.3 创建一个业务类接口
如图,建立对应的软件包和接口,并在接口创建方法:
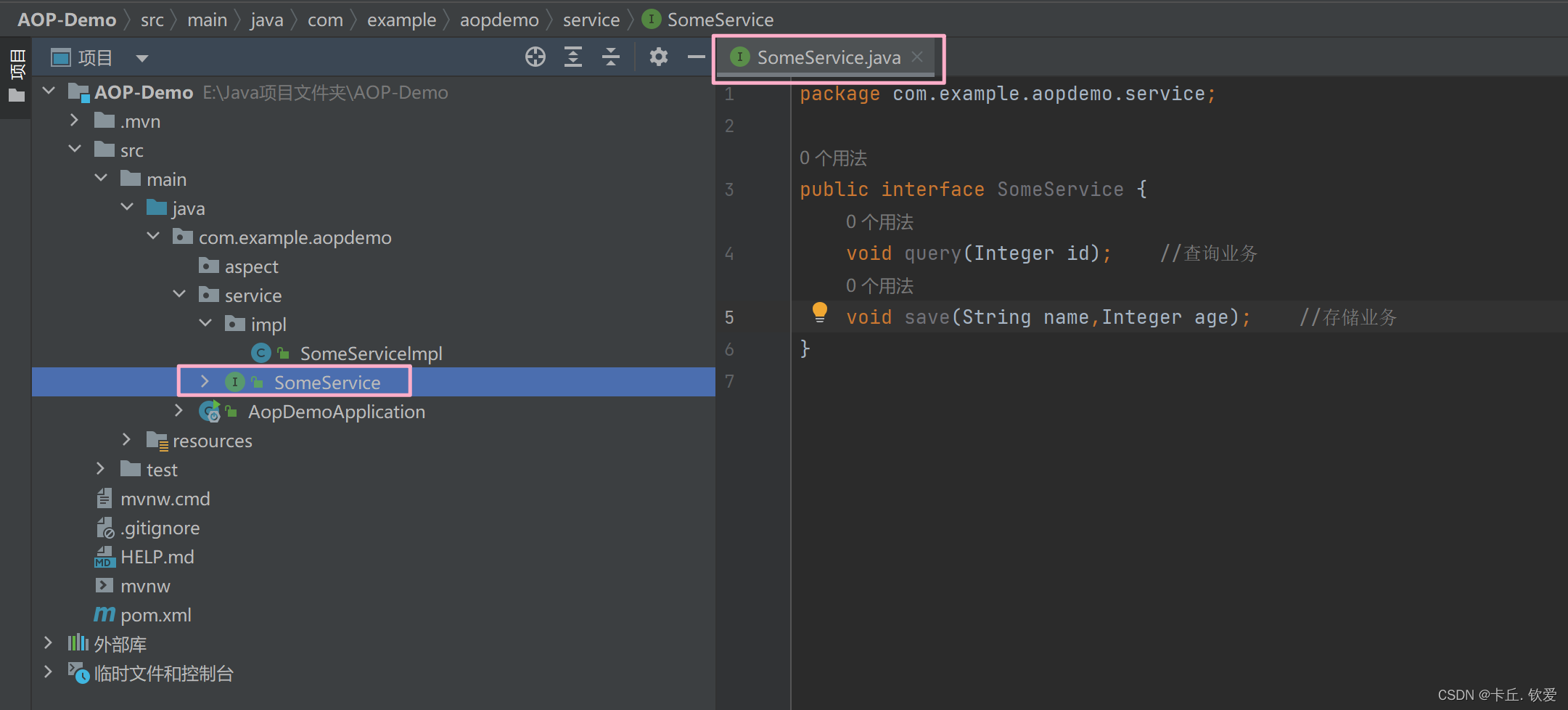
2.4 在实体类实现接口业务
注意,一定要添加Service注解

2.5 在单元测试运行结果


2.6 创建切面类



import org.aspectj.lang.JoinPoint;
import org.aspectj.lang.annotation.Aspect;
import org.aspectj.lang.annotation.Before;
import org.springframework.stereotype.Component;import java.time.LocalDateTime;
import java.time.format.DateTimeFormatter;
import java.util.StringJoiner;@Component
@Aspect
public class LogAspect {@Before("execution(* com.example.aopdemo.service..*.*(..))")public void sysLog(JoinPoint jp){StringJoiner log = new StringJoiner("|","{","}");DateTimeFormatter formatter = DateTimeFormatter.ofPattern("yyy-MM-dd HH:mm:ss");log.add(formatter.format(LocalDateTime.now()));//当前执行的业务方法名称String methodName = jp.getSignature().getName();log.add(methodName);//方法的参数Object[] args = jp.getArgs();for(Object arg:args){log.add(arg == null ? "-" : arg.toString() );}System.out.println("AOP日志启动!" + log);}
2.7 再次运行测试
再次运行就发发现我们的日志已经添加进去了,并且没有对原代码进行改变,这就是AOP的丝滑之处。
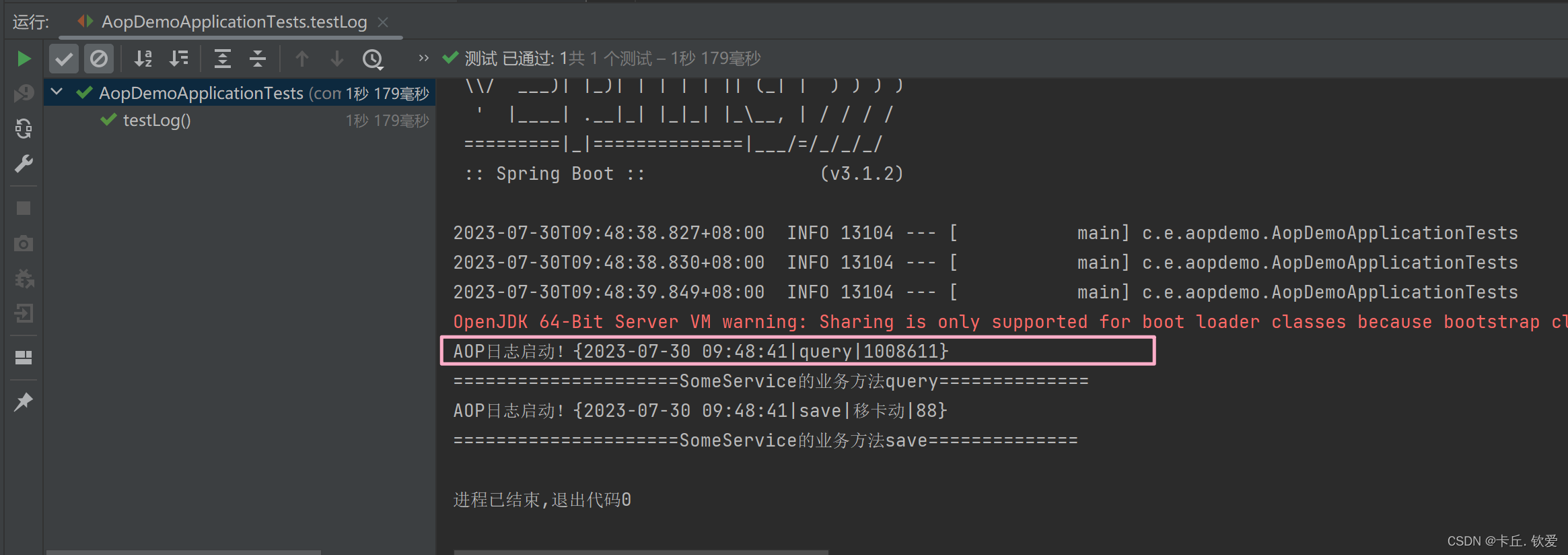
总结
AOP使用横向抽取机制,取代纵向集成体系的重复代码建设。使用Aspect,使业务逻辑只关注业务本身,将日志管理、事务处理、性能统计、异常处理、权限控制等代码从业务逻辑代码中抽离,从而实现改变这些行为的时候不影响业务逻辑代码。实乃开发必备之神器也,本文到此就结束了,希望大家可以有所收获~
相关文章:

使用Spring Boot AOP实现日志记录
目录 介绍 1.1 什么是AOP 1.2 AOP体系与概念 AOP简单实现 2.1 新建一个SpringBoot项目,无需选择依赖 2.2 设置好本地Maven配置后,在pom.xml文件里添加添加maven依赖 2.3 创建一个业务类接口 2.4 在实体类实现接口业务 2.5 在单元测试运行结果 …...

图像中不规则物体的长轴与短轴:OpenCV实现指南
1.首先,读取图像并将其转换为灰度图像。 2.进行图像预处理,包括使用高斯模糊和阈值化,以便更好地处理图像。 3.通过使用OpenCV的cv2.findContours()函数,找到图像中的所有轮廓。 4.遍历所有轮廓,如果轮廓点的数量大…...
C/C++开发,opencv与qt结合播放视频
目录 一、qt_ui创建 1.1 ui设置 1.2 ui及代码输出保存 二、创建工程 2.1 工程目录及编译设置 2.2 源码设计 三、编译及测试 3.1 程序编译 3.2 程序运行 首先声明,这是一个OpenCV 3学习文档的案例,但是说明有些过于省略,只有一些简短的代码…...

磁共振图像处理中 fft1c 和 ifft1c 函数的 Python 实现
fft1c 和 ifft1c 是 MRI 图像处理的常用函数。通常使用如下的 Matlab 实现 (Michael Lustig,2005) function res ifft1c(x,dim)% res fft1c(x) % % orthonormal forward 1D FFT %nsize(x,dim); shftzeros(1,5); shft(dim)ceil(n/2);xcirc…...

阿里云国际站香港地域服务器访问延迟丢包的原因及解决方法
阿里云百科有2台香港地域的轻量应用服务器,国内使用发现Ping值延迟丢包严重,从大陆到香港访问是经过国际链路和运营商国际路由节点,会受到到国际链路拥塞,以及运营商出境路由限制,导致无法正常连接或访问某些网站&…...

GULI PART.1
文章目录 1、尚硅谷-谷粒学院1.1、系统功能模块介绍1.2、系统开发方式 2、Mybatis-Plus2.1、什么是 MyBatis?2.2、什么是Mybatis-Plus?2.3、Mybatis-plus 的特性2.4、支持的数据库 3、Mybatis-Plus入门3.1、创建表和数据3.2、创建SpringBoot工程3.3、安装…...

NetApp FAS2750 和 FAS2820:适用于分布式企业和从远程到核心的 FAS
NetApp FAS2750 和 FAS2820:适用于分布式企业和从远程到核心的 FAS 拥有分布式企业和多个办公位置的客户希望使用这些系统进行虚拟化,以及为大型 FAS 和 AFF 系统提供简单且经济高效的备份和灾难恢复。 为什么要从 NetApp FAS 系列中选择一个型号&…...

剑指YOLOv8改进最新MPDIoU损失函数:超越现有多种G/D/C/EIoU,23年7月首发论文,高效准确的边界框回归的损失
💡本篇内容:剑指YOLOv8改进最新MPDIoU损失函数:超越现有多种G/D/C/EIoU,23年7月首发论文,高效准确的边界框回归的损失 💡🚀🚀🚀本博客 改进源代码改进 适用于 YOLOv8 按步骤操作运行改进后的代码即可 💡:重点:该专栏《剑指YOLOv8原创改进》只更新改进 YOLO…...
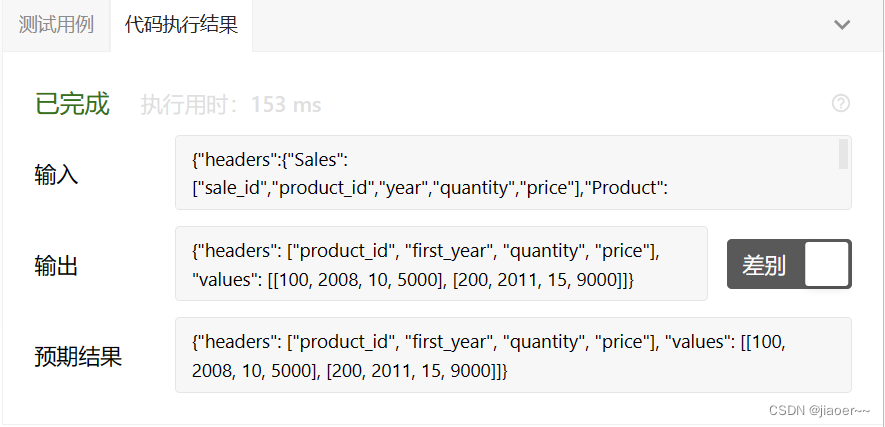
SQL-每日一题【1070. 产品销售分析 III】
题目 销售表 Sales: 产品表 Product: 编写一个 SQL 查询,选出每个销售产品 第一年 销售的 产品 id、年份、数量 和 价格。 结果表中的条目可以按 任意顺序 排列。 查询结果格式如下例所示: 示例 1: 解题思路 前置知…...

为何押注AI大模型的微软云,业绩增速反而不如谷歌云?
科技云报道原创。 上周微软、谷歌、Meta等国外科技公司相继发布最新财报。作为与人工智能、云计算和数字广告等领域相关的巨头,它们的一举一动都将对市场产生影响,同时也吸引着众多从业者的关注。 在国外三大云巨头中,谷歌云的市场份额长期…...

CDN加速服务的工作原理
CDN(内容分发网络)加速服务是一种用于提高网站和应用性能的技术,通过将内容分发到全球多个节点,使用户可以从就近的节点获取所需内容,从而实现更快的加载速度和更稳定的访问体验。下面详细介绍CDN加速服务的工作原理&a…...
)
在CSDN学Golang云原生(Kubernetes Service)
一,service的定义与基本用法 在 Kubernetes 中,Service 是一种抽象概念,用于定义一组 Pod 并为它们提供访问入口。通过 Service,您可以将多个 Pod 组合成一个逻辑单元,并使用标签选择器来确定哪些 Pod 属于该 Service…...

【数据结构篇C++实现】- 图
友情链接:C/C系列系统学习目录 文章目录 🚀一、图的基本概念和术语1、有向图和无向图3、基本图和多重图4、完全图5、子图6、连通、连通图和连通分量7、强连通图、强连通分量8、生成树、生成森林9、顶点的度、入度和出度10、边的权和网11、稠密图、稀疏图…...

Sentinel持久化规则
项目中有用到Sentinel,然后需要将Sentinel上配置的规则做持久化(或者初始化),通过改写Sentinel源码实现了需求,下面记录一下实现过程。 如果不知道Sentinel怎么搭,可以看看: 流控平台Sentinel搭建和接入教程_东皋长歌的博客-CSDN博客 一,背景 Sentinel是Alibaba开源…...
list与sort()
运行代码: //list与sort() #include"std_lib_facilities.h" //声明Item类 struct Item {string name;int iid;double value;Item():name(" "),iid(0),value(0.0){}Item(string ss,int ii,double vv):name(ss),iid(ii),value(vv){}friend istre…...

6个月、21天,GoldenDB分布式数据库核心系统落地中移动
近日,2023“鼎新杯”数字化转型应用大赛入围名单公示,山东移动基于GoldenDB分布式数据库的CRM&BOSS核心系统自主创新实践成功入选。该项目是中兴通讯与中国移动在数据库关键领域的又一个合作范例。 核心系统业务量大,分布式转型迫在眉睫 …...
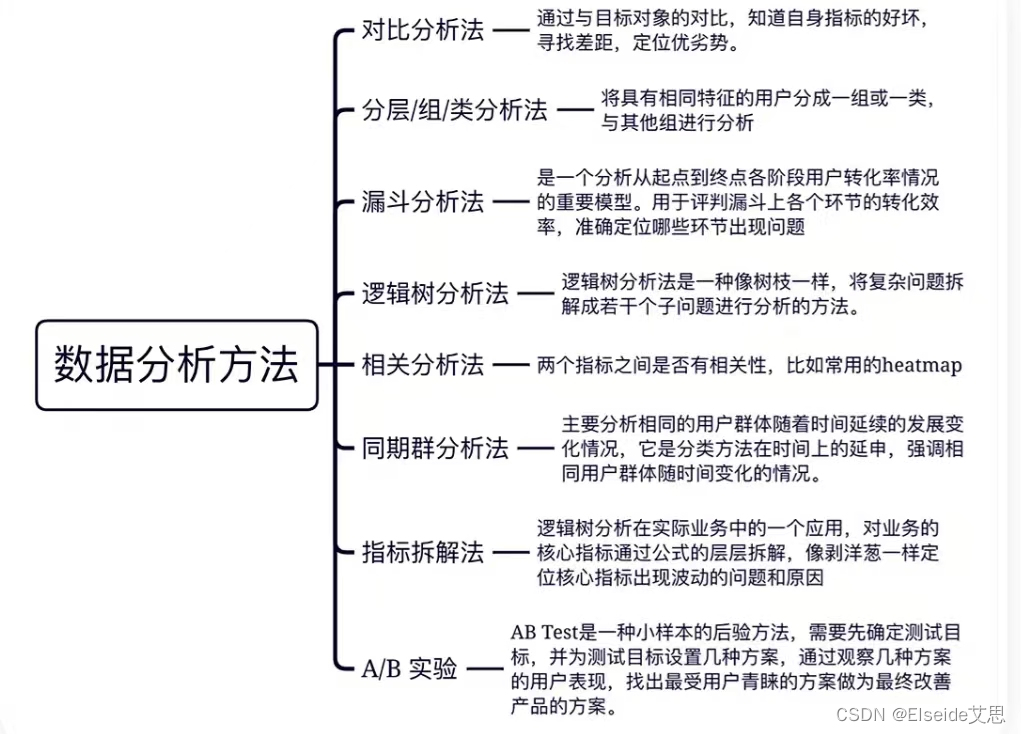
如何正确培养数据思维?
在大数据时代,数据思维已成了每个人的必备品。下面,我们就来了解一下,什么是数据思维。不过要想弄懂什么是数据思维,首先来打破大家对数据的错误认知,数据不仅仅指数字。 1. 数据思维是什么? 百度百科对数…...

JavaScript中的?.和??的用法
1、?.(可选链运算符) 在JavaScript中,"?.“是一种叫做"Optional Chaining”(可选链)的新操作符。它允许我们在访问一个可能为null或undefined的属性或调用一个可能不存在的方法时,避免出现错误…...

Git for linux
<1> linux 安装git sudo apt-get install git-all <2> 创建git,分为两部分,远程网络部分和本地主机部分 远程网路:登录GitHub: Let’s build from here GitHub 注册帐号,创建登录密码,此密码很长&a…...
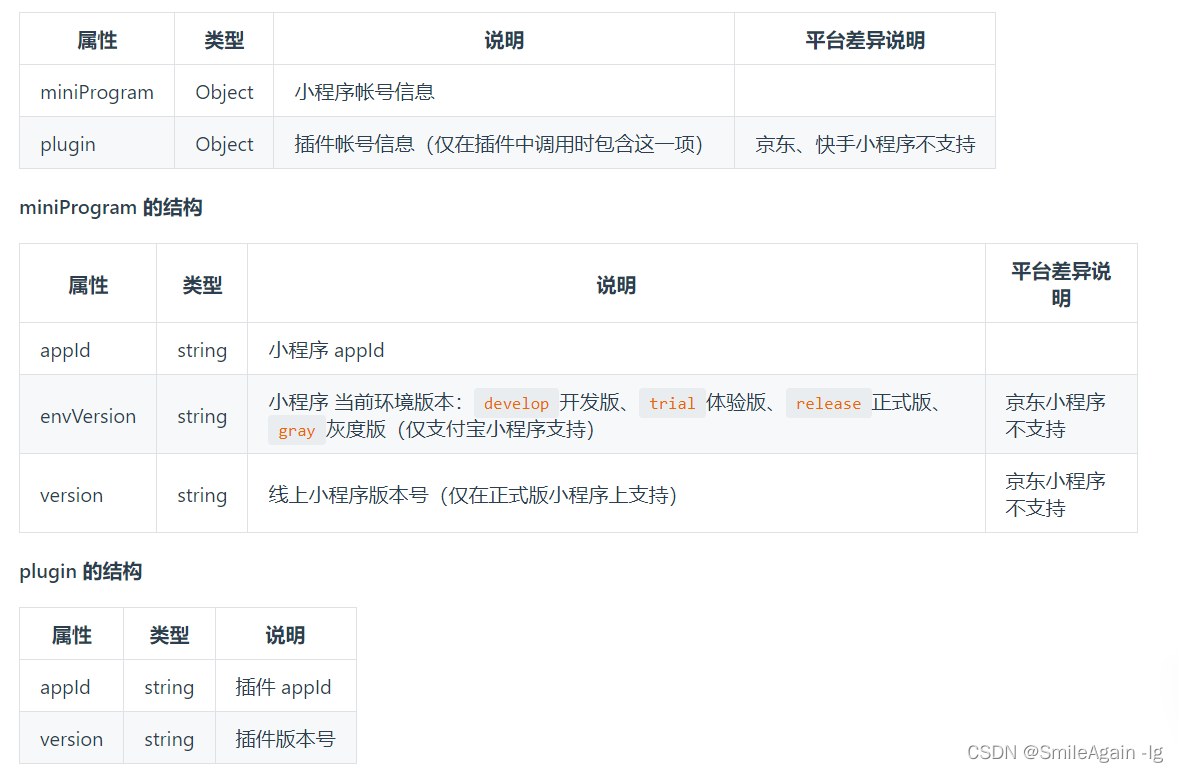
uniapp小程序,根据小程序的环境版本,控制的显页面功能按钮的示隐藏
需求:根据小程序环境控制控制页面某个功能按钮的显示隐藏; 下面是官方文档和功能实现的相关代码: 实现上面需要,用到了uni.getAccountInfoSync(): uni.getAccountInfoSync() 是一个 Uniapp 提供的同步方法,…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...
