数学学习——最优化问题引入、凸集、凸函数、凸优化、梯度、Jacobi矩阵、Hessian矩阵
文章目录
- 最优化问题引入
- 凸集
- 凸函数
- 凸优化
- 梯度
- Jacobi矩阵
- Hessian矩阵
最优化问题引入
例如:有一根绳子,长度一定的情况下,需要如何围成一个面积最大的图像?这就是一个最优化的问题。就是我们高中数学中最常见的最值问题。
最优化问题的一般形式是:
m i n f ( x ) x ∈ C minf(x) \\ x \in C minf(x)x∈C
其中, f f f是目标函数, A A A是约束条件, x x x是参数值。要求解最优化问题,就是要找到一个可行解 x ∗ x^∗ x∗,使得对于所有的 x ∈ A x\in A x∈A,都有 f ( x ∗ ) ≤ f ( x ) f(x^∗)≤f(x) f(x∗)≤f(x)。
最优化问题的三个基本要素是:
- 目标函数:用来衡量结果的好坏
- 参数值:未知的因子,需要通过数据来确定
- 约束条件:需要满足的限制条件
凸集
定义:集合 C C C中任意两点的线 C C C中,则称集合 C C C为凸集,也即满足 ∀ x , y ∈ C , 0 ≤ 0 ≤ 1 \forall x,y\in C,0≤0≤1 ∀x,y∈C,0≤0≤1有 8 x + ( 1 − ) y ∈ C 8x+(1-)y\in C 8x+(1−)y∈C的集合称为凸集。
凸集合就是一个集合中的任意两点之间的线段都属于这个集合,而非凸集合就是不满足这个条件的集合。
凸集合:
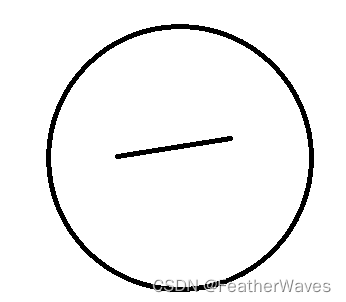
非凸集合:
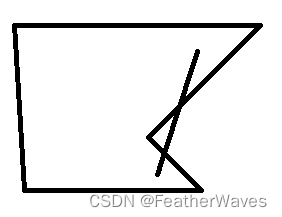
凸函数
定义:凸函数是一种定义在凸集上的实值函数,满足任意两点连成的线段上的函数值不大于两点的函数值的加权平均。也就是说,如果 f f f是凸函数,那么对于任意 x x x和 y y y在定义域内,以及任意 θ θ θ在 ( 0 , 1 ) (0,1) (0,1)之间,有
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
这个不等式称为凸函数的凸性条件。如果不等式中的等号只在 x = y x=y x=y时成立,那么 f f f是严格凸的。如果不等式反向成立,那么 f f f是凹函数。如果 f f f既是凸函数又是凹函数,那么 f f f是仿射函数。
二维空间的凸函数:
import numpy as np
import matplotlib.pyplot as plt# 定义凸函数 f(x) = x^2
def f(x):return x**2# 生成x轴的数据
x = np.linspace(-5, 5, 100)# 计算y轴的数据
y = f(x)# 画出函数图像
plt.plot(x, y)# 设置坐标轴标签和标题
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Convex Function')# 显示图像
plt.show()
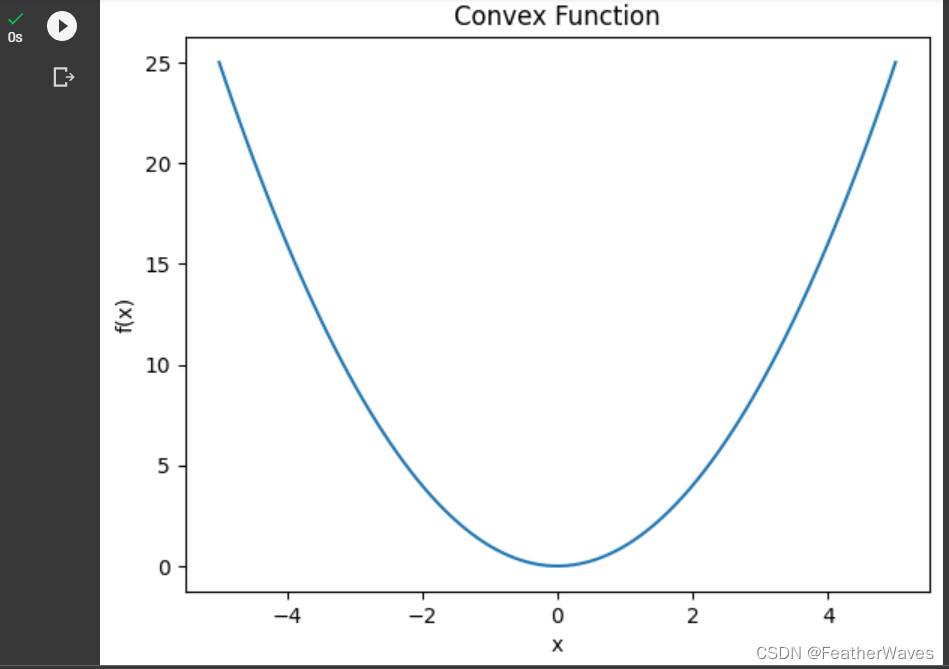
三维空间的凸函数:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np# 定义凸函数 f(x,y) = x^2 + y^2
def f(x, y):return x**2 + y**2# 生成x和y轴的数据
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)# 将x和y轴数据转换为网格矩阵
X, Y = np.meshgrid(x, y)# 计算z轴的数据
Z = f(X, Y)# 创建3D图像对象
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')# 画出函数图像
ax.plot_surface(X, Y, Z)# 设置坐标轴标签和标题
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
ax.set_title('Convex Function')# 显示图像
plt.show()
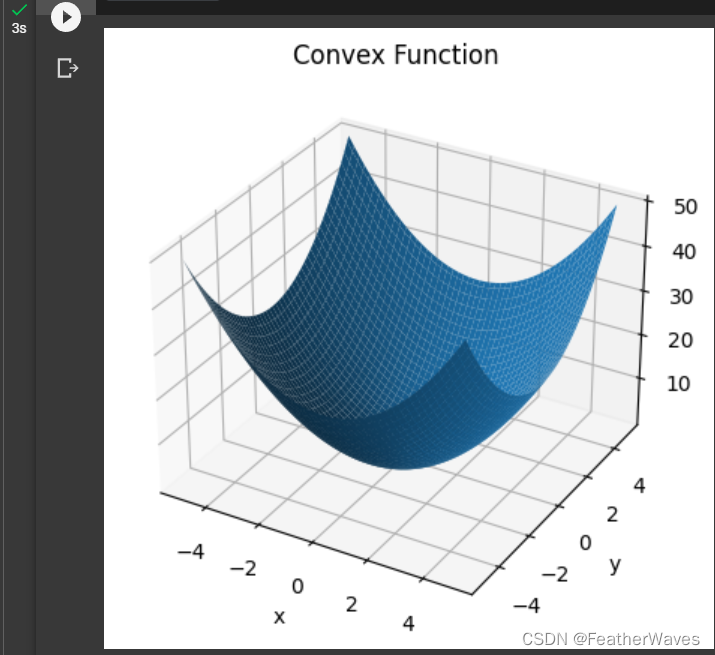
二维空间的非凹非凸函数:
import numpy as np
import matplotlib.pyplot as plt# 定义非凹非凸函数 f(x) = sin(x) + cos(2x)
def f(x):return np.sin(x) + np.cos(2*x)# 生成x轴的数据
x = np.linspace(-5, 5, 100)# 计算y轴的数据
y = f(x)# 画出函数图像
plt.plot(x, y)# 设置坐标轴标签和标题
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Non-convex Function')# 显示图像
plt.show()
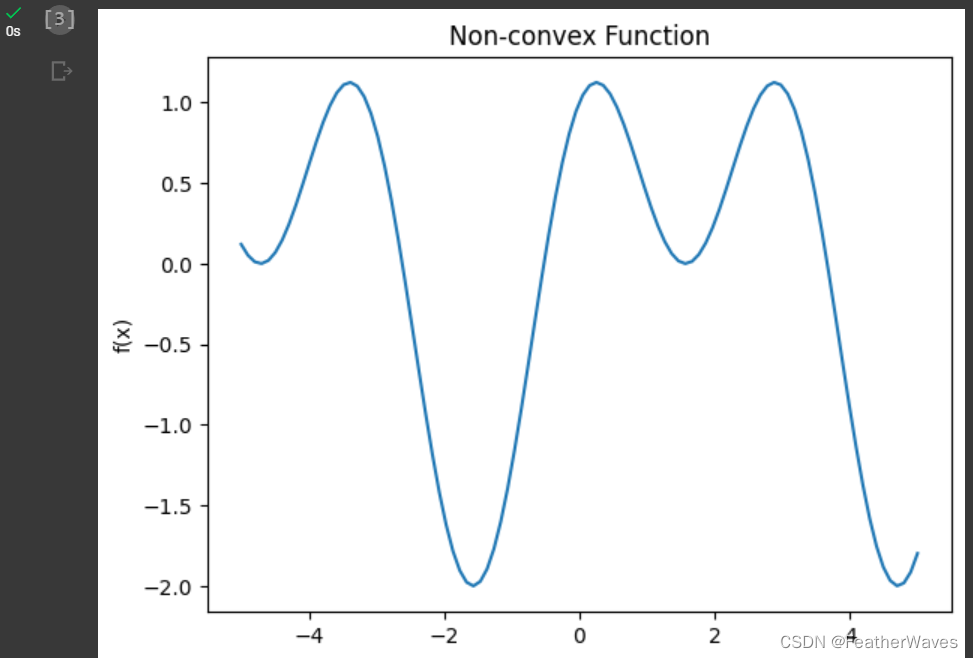
三维空间的非凹非凸函数:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np# 定义非凹非凸函数 f(x,y) = sin(x) + cos(2y)
def f(x, y):return np.sin(x) + np.cos(2*y)# 生成x和y轴的数据
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)# 将x和y轴数据转换为网格矩阵
X, Y = np.meshgrid(x, y)# 计算z轴的数据
Z = f(X, Y)# 创建3D图像对象
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')# 画出函数图像
ax.plot_surface(X, Y, Z)# 设置坐标轴标签和标题
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
ax.set_title('Non-convex Function')# 显示图像
plt.show()
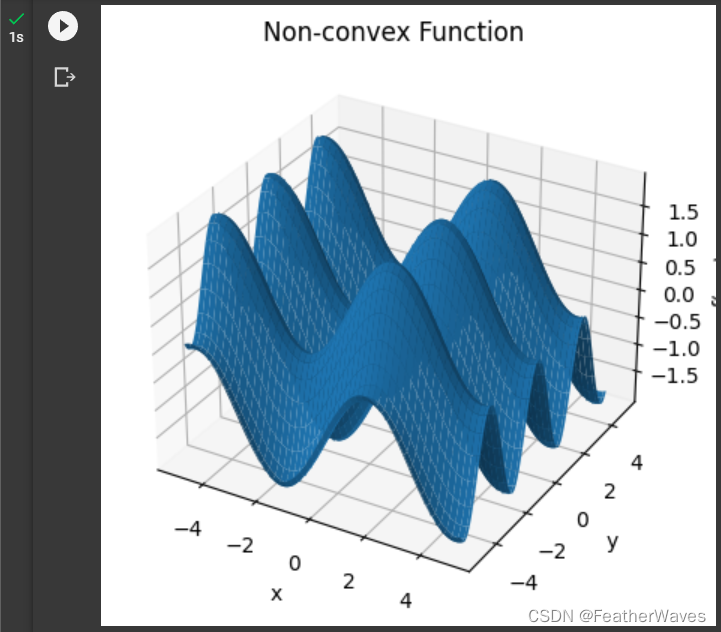
凸优化
凸优化是数学最优化的一个子领域,研究定义在凸集中的凸函数最小化的问题。
凸优化问题可以形式化地写成:
m i n f ( x ) s . t . g i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m h j ( x ) = 0 , j = 1 , 2 , ⋯ , n \begin{align*} min&f(x) \\ s.t. &g_i(x)≤0,i=1,2,\cdots,m\\ &h_j(x)=0,j=1,2,\cdots,n \end{align*} mins.t.f(x)gi(x)≤0,i=1,2,⋯,mhj(x)=0,j=1,2,⋯,n
其中x为优化变量; f f f为凸目标函数; g i g_i gi和 h j h_j hj为约束函数,分别表示不等式约束和等式约束;
这个问题的意思是求解最小化目标函数 f ( x ) f(x) f(x),使得x满足不等式约束 g i ( x ) ≤ 0 g_i(x)≤0 gi(x)≤0和等式约束 h j ( x ) = 0 h_j(x)=0 hj(x)=0。
一个凸优化问题具备如下性质:
- 凸优化的局部极小点就是全局极小点:
- 如果目标函数是严格凸函数,则凸优化问题具有唯一的全局极小点:
- 凸优化的全局极大点必定能在可行域的边界上达到;
梯度
它表示一个多元函数在某一点沿着最大增长方向的变化率,可以用偏导数来表示。梯度是一个向量,它的方向是函数在该点最大增长的方向,它的大小是在该方向上的增长率。梯度可以用向量微分算子(nabla)来表示。
例如:
∇ f ( x , y ) = ∂ f ∂ x i + ∂ f ∂ y j \nabla f(x,y) = \frac{\partial f}{\partial x}i+\frac{\partial f}{\partial y}j ∇f(x,y)=∂x∂fi+∂y∂fj
Jacobi矩阵
定义: 雅可比矩阵是一个函数的一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。雅可比矩阵反映了一个函数在给定点的最佳线性逼近,类似于单变量函数的导数。如果函数是从 R n ℝ_n Rn到 R m ℝ_m Rm的映射,那么它的雅可比矩阵是一个 m × n m \times n m×n的矩阵,可以用以下方式定义:
J = [ ∂ f 1 ∂ x 1 ⋯ ∂ f 1 ∂ x n ⋮ ⋱ ⋮ ∂ f m ∂ x 1 ⋯ ∂ f m ∂ x n ] J = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix} J= ∂x1∂f1⋮∂x1∂fm⋯⋱⋯∂xn∂f1⋮∂xn∂fm
其中 f i f_i fi是函数的第 i i i个分量, x j x_j xj是第 j j j个自变量。雅可比矩阵的符号表示为 J f J_f Jf或者 ∂ ( f 1 , ⋯ , f m ) ∂ ( x 1 , ⋯ , x m ) \frac{\partial {(f_1,\cdots, f_m)}}{\partial {(x_1,\cdots, x_m)}} ∂(x1,⋯,xm)∂(f1,⋯,fm)。雅可比矩阵的第 i i i行是由函数 f i f_i fi的梯度向量表示的。
举例:
设有函数 F : R 3 → R 4 F:ℝ^3 \to ℝ^4 F:R3→R4,其分量为:
w = x + y + z x = x y = y z = z w=x+y+zx=xy=yz=z w=x+y+zx=xy=yz=z
雅可比矩阵是:
J ( F ) = ∣ ∂ w ∂ x ∂ w ∂ y ∂ w ∂ z ∂ x ∂ x ∂ x ∂ y ∂ x ∂ z ∂ y ∂ x ∂ y ∂ y ∂ y ∂ z ∂ z ∂ x ∂ z ∂ y ∂ z ∂ z ∣ J(F) = \begin{vmatrix} \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \\ \frac{\partial x}{\partial x} & \frac{\partial x}{\partial y} & \frac{\partial x}{\partial z} \\ \frac{\partial y}{\partial x} & \frac{\partial y}{\partial y} & \frac{\partial y}{\partial z} \\ \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} & \frac{\partial z}{\partial z} \end{vmatrix} J(F)= ∂x∂w∂x∂x∂x∂y∂x∂z∂y∂w∂y∂x∂y∂y∂y∂z∂z∂w∂z∂x∂z∂y∂z∂z
将给定的函数代入上式子,得到:
J ( F ) = ∣ 1 1 1 y x 0 0 z y 0 0 1 ∣ J(F) = \begin{vmatrix} 1 & 1 & 1 \\ y & x & 0 \\ 0 & z & y\\ 0 & 0 & 1 \end{vmatrix} J(F)= 1y001xz010y1
Hessian矩阵
H e s s i a n Hessian Hessian矩阵是一个多元函数的二阶偏导数构成的方阵,用于描述函数的局部曲率。如果函数 f : R n → R f:R^n→R f:Rn→R在点 x x x处具有连续的二阶偏导数,那么它的 H e s s i a n Hessian Hessian矩阵 H f ( x ) H_f(x) Hf(x)定义为:
H f ( x ) = [ ∂ 2 f ∂ x 1 2 ( x ) ⋯ ∂ 2 f ∂ x 1 ∂ x n ( x ) ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ( x ) ⋯ ∂ 2 f ∂ x n 2 ( x ) ] H_f(x) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2}(x) & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n}(x) \\ \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1}(x) & \cdots & \frac{\partial^2 f}{\partial x_n^2}(x) \end{bmatrix} Hf(x)= ∂x12∂2f(x)⋮∂xn∂x1∂2f(x)⋯⋱⋯∂x1∂xn∂2f(x)⋮∂xn2∂2f(x)
H e s s i a n Hessian Hessian矩阵和 J a c o b i Jacobi Jacobi矩阵之间的关系是, H e s s i a n Hessian Hessian矩阵等于函数的梯度的 J a c o b i Jacobi Jacobi矩阵。也就是说,如果 f : R n → R f:Rn→R f:Rn→R,那么
H f ( x ) = J ∇ f ( x ) H_f(x)=J_{\nabla f}(x) Hf(x)=J∇f(x)
其中 ∇ f \nabla f ∇f表示函数f的梯度, J ∇ f J_{\nabla f} J∇f表示梯度 ∇ f \nabla f ∇f的 J a c o b i Jacobi Jacobi矩阵。这个关系可以从 H e s s i a n Hessian Hessian矩阵和 J a c o b i Jacobi Jacobi矩阵的定义直接得到。
举例:
有个二元函数是 f ( x , y ) = x 2 + y 2 f(x,y)=x2+y2 f(x,y)=x2+y2。它的梯度是 ∇ f ( x , y ) = ( 2 x , 2 y ) ∇f(x,y)=(2x,2y) ∇f(x,y)=(2x,2y),它的 H e s s i a n Hessian Hessian矩阵是
J ( F ) = ∣ ∂ 2 f ∂ x 2 ( x , y ) ∂ 2 f ∂ x ∂ y ( x , y ) ∂ 2 f ∂ y ∂ x ( x , y ) ∂ 2 f ∂ y 2 ( x , y ) ∣ = ∣ 2 0 0 2 ∣ J(F) = \begin{vmatrix} \frac{\partial^2 f}{\partial x^2}(x, y) & \frac{\partial^2 f}{\partial x \partial y} (x, y)\\ \frac{\partial^2 f}{\partial y \partial x}(x, y) & \frac{\partial^2 f}{\partial y^2} (x, y) \end{vmatrix} = \begin{vmatrix} 2 & 0 \\ 0 & 2 \end{vmatrix} J(F)= ∂x2∂2f(x,y)∂y∂x∂2f(x,y)∂x∂y∂2f(x,y)∂y2∂2f(x,y) = 2002
它的梯度的 J a c o b i Jacobi Jacobi矩阵是
J ( F ) = ∣ ∂ ∂ x ( 2 x ) ∂ ∂ y ( 2 x ) ∂ ∂ x ( 2 y ) ∂ ∂ y ( 2 y ) ∣ = ∣ 2 0 0 2 ∣ J(F) = \begin{vmatrix} \frac{\partial }{\partial x}(2x) & \frac{\partial }{\partial y}(2x) \\ \frac{\partial }{\partial x}(2y) & \frac{\partial }{\partial y}(2y) \end{vmatrix} = \begin{vmatrix} 2 & 0 \\ 0 & 2 \end{vmatrix} J(F)= ∂x∂(2x)∂x∂(2y)∂y∂(2x)∂y∂(2y) = 2002
可以看出,它们是相等的。
相关文章:

数学学习——最优化问题引入、凸集、凸函数、凸优化、梯度、Jacobi矩阵、Hessian矩阵
文章目录 最优化问题引入凸集凸函数凸优化梯度Jacobi矩阵Hessian矩阵 最优化问题引入 例如:有一根绳子,长度一定的情况下,需要如何围成一个面积最大的图像?这就是一个最优化的问题。就是我们高中数学中最常见的最值问题。 最优化…...
HCIP期中实验
考试需求 1 、该拓扑为公司网络,其中包括公司总部、公司分部以及公司骨干网,不包含运营商公网部分。 2 、设备名称均使用拓扑上名称改名,并且区分大小写。 3 、整张拓扑均使用私网地址进行配置。 4 、整张网络中,运行 OSPF 协议…...

【Git系列】IDEA集成Git
🐳IDEA集成Git 🧊1. idea配置git🧊2. idea添加暂存区和提交🪟创建文件🪟将整个项目添加到暂存区🪟提交到本地仓库🪟查看控制台,显示提交的信息🪟修改文件,再次…...
短视频矩阵源码开发搭建分享--多账号授权管理
目录 文章目录 前言 一、矩阵号系统是什么? 二、使用步骤 1.创建推广项目 2.多账号授权 3.企业号智能客服系统 总结 前言 短视频多账号矩阵系统,通过多账号一键授权管理的方式,为运营人员打造功能强大及全面的“矩阵式“管理平台。…...
数据中台系列2:rabbitMQ 安装使用之 window 篇
RabbitMQ 是一个开源的消息队列系统,是高级消息队列协议(AMQP)的标准实现,用 erlang 语言开发。 因此安装 RabbitMQ 之前要先安装好 erlang。 1、安装 erlang 到 这里 下载本机能运行的最新版 erlang 安装包。如果本机没有装过 …...
Windows驱动开发
开发Windows驱动程序时,debug比较困难,并且程序容易导致系统崩溃,这时可以使用Virtual Box进行程序调试,用WinDbg在主机上进行调试。 需要使用的工具: Virtual Box:用于安装虚拟机系统,用于运…...

汽车分析,随时间变化的燃油效率
简述 今天我们来分析一个汽车数据。 数据集由以下列组成: 名称:每辆汽车的唯一标识符。MPG:燃油效率,以英里/加仑为单位。气缸数:发动机中的气缸数。排量:发动机排量,表示其大小或容量。马力&…...

大数据面试题之Elasticsearch:每日三题(六)
大数据面试题之Elasticsearch:每日三题 1. 为什么要使用Elasticsearch?2.Elasticsearch的master选举流程?3.Elasticsearch集群脑裂问题? 1. 为什么要使用Elasticsearch? 系统中的数据,随着业务的发展,时间…...
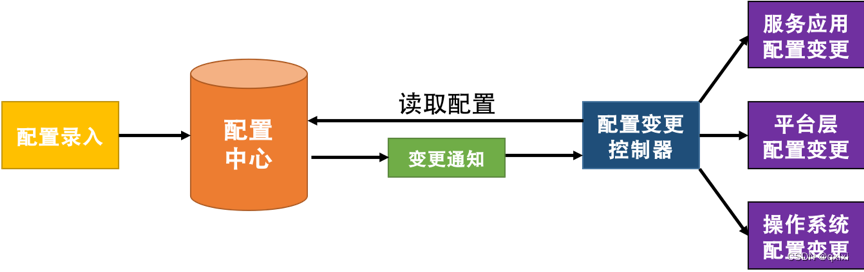
【管理设计篇】聊聊分布式配置中心
为什么需要配置中心 对于一个软件系统来说,除了数据、代码,还有就是软件配置,比如操作系统、数据库配置、服务配置 端口 ip 、邮箱配置、中间件软件配置、启动参数配置等。如果说是一个小型项目的话,可以使用Spring Boot yml文件…...

远程控制平台简介
写在前面 之所以想自己动手实现一个远程控制平台,很大一部分原因是因为我那糟糕的记性,虽然经常加班到很晚,拖着疲惫的步伐回到家,才想起忘记打卡了,如果我能在家控制在办公室的手机打一下卡就好了… 有人说,市场上有TeamViewer,向日葵,AnyDesk,ToDesk,等等这些老大…...
韦东山Linux驱动入门实验班(5)LED驱动---驱动分层和分离,平台总线模型
前言 (1)前面已经已经详细介绍了LED驱动如何进行编写的代码。如果韦东山Linux驱动入门实验班(4)LED驱动已经看懂了,驱动入门实验班后面的那些模块实验,其实和单片机操作差不太多了。我就不再浪费时间进行讲…...

【雕爷学编程】MicroPython动手做(02)——尝试搭建K210开发板的IDE环境
知识点:简单了解K210芯片 2018年9月6日,嘉楠科技推出自主设计研发的全球首款基于RISC-V的量产商用边缘智能计算芯片勘智K210。该芯片依托于完全自主研发的AI神经网络加速器KPU,具备自主IP、视听兼具与可编程能力三大特点,能够充分适配多个业务场景的需求。作为嘉楠科…...

C#——Thread与Task的差异比较及使用环境
C#——Thread与Task的差异比较及使用环境 前言一、差异1. 创建和管理:2. 异步编程:3. 返回值:4. 异常处理:5. 线程复用: 总结 前言 前面两篇文章,分别通过各自的实例讲了关于Task以及Thread的相关的使用特…...

刷题 31-35
三十一、 747. 至少是其他数字两倍的最大数 给你一个整数数组 nums ,其中总是存在 唯一的 一个最大整数 。 请你找出数组中的最大元素并检查它是否 至少是数组中每个其他数字的两倍 。如果是,则返回 最大元素的下标 ,否则返回 -1 。 示例 1&a…...

【mysql】—— 数据类型详解
序言: 本期我将大家认识关于 mysql 数据库中的基本数据类型的学习。通过本篇文章,我相信大家对mysql 数据类型的理解都会更加深刻。 目录 (一)数据类型分类 (二)数值类型 1、tinyint类型 2、bit类型 …...

kafka常用命令
查看主题 ./kafka-topics.sh --list --bootstrap-server 10.1.1.2:9092 创建主题 ./kafka-topics.sh --bootstrap-server 10.1.1.2:9092 --create --topic test_topic --partitions 1 查看消费者列表--list ./kafka-consumer-groups.sh --bootstrap-server 10.1.1.2:9092 -…...
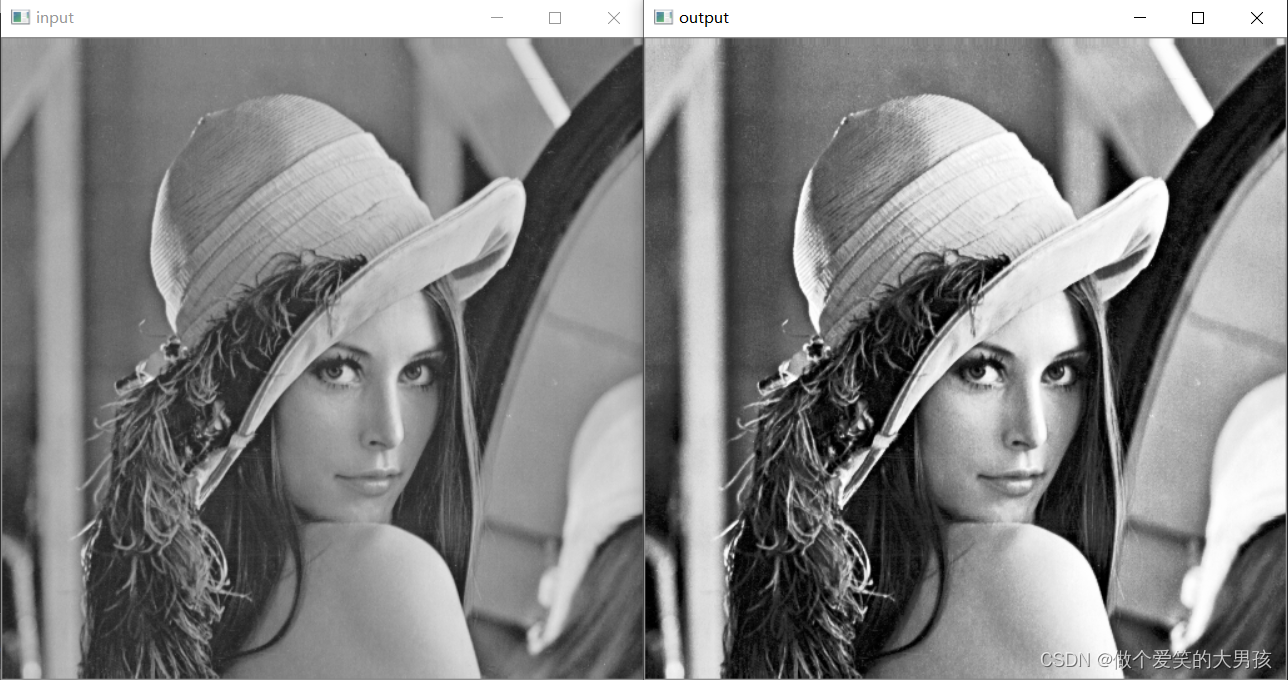
数字图像处理(番外)图像增强
图像增强 图像增强的方法是通过一定手段对原图像附加一些信息或变换数据,有选择地突出图像中感兴趣的特征或者抑制(掩盖)图像中某些不需要的特征,使图像与视觉响应特性相匹配。 图像对比度 图像对比度计算方式如下: C ∑ δ δ ( i , j …...

flutter:轮播
前言 介绍几个比较有不错的轮播库 swipe_deck 与轮播沾边,但是更多的是一种卡片式的交互式界面设计。它的主要概念是用户可以通过左右滑动手势浏览不同的卡片,每张卡片上都有不同的信息或功能。 Swipe deck通常用于展示图片、产品信息、新闻文章、社…...

高忆管理:股票投资策略是什么?有哪些?
在进行股票买卖过程中,出资者需求有自己的方案和出资战略,并且主张严格遵从出资战略买卖,不要跟风操作。那么股票出资战略是什么?有哪些?下面就由高忆管理为我们剖析: 股票出资战略简略来说便是能够协助出资…...
为公网SSH远程Ubuntu配置固定的公网TCP端口地址主图
文章目录 为公网SSH远程Ubuntu配置固定的公网TCP端口地址 为公网SSH远程Ubuntu配置固定的公网TCP端口地址 在上篇文章中,我们通过cpolar建立的临时TCP数据隧道,成功连接了位于其他局域网下的Ubuntu系统,实现了不同操作系统、不同网络下的系统…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
